Пример расчета зубчатой передачи

1. Пример расчета цилиндрической косозубой передачи

2.

Выполнить проектный и проверочный расчеты для закрытой цилиндрической
косозубой передачи. Для решения воспользоваться данными полученными на
стадиях кинематического расчета и выбора материала
2
Дано: Pт 5,36 кВт;
3
nт 88,18 об мин
т 9,23 с 1
Tт 580,72 Н м
u зп 5;
1
M
Pт , nт
[ ]Н 434,7 МПа
[ ]F 211 МПа
1
[ ]F 188 МПа
2
1 – ременная передача
2 – цилиндрический редуктор
3 – цепная передача

3.

Проектный расчет
Определяем межосевое расстояние передачи:
T2 103
a К а (u зп 1) 3
K Н
2
2
ba u зп [ ]Н
где Kа – вспомогательный коэффициент
для косозубых и шевронных передач Kа = 43
для прямозубых передач Kа = 49,5
Переводная формула
ba u зп 1
2
KH – коэффициент неравномерности нагрузки по длине зуба.
«+» для внешнего зацепления
для прирабатывающихся зубьев при твердости < 350 HB KH = 1,15
«-» для внутреннего зацепления
при твердости > 350 HB определяется по таблице
bd b2 / d1
Расположение шестерни
относительно опор
Твердость, НВ
bd
0,2
0,4
0,6
0,8
1,2
1,6
Консольное, опоры
шарикоподшипники
350
> 350
1,08
1,2
1,17
1,44
1,28
Консольное, опоры
роликоподшипники
350
> 350
1,06
1,11
1,12
1,25
1,19
1,45
1,27
Симметричное
350
> 350
1,01
1,01
1,02
1,02
1,03
1,04
1,04
1,07
1,07
1,16
1,11
1,26
Несимметричное
350
> 350
1,03
1,06
1,05
1,12
1,07
1,2
1,12
1,29
1,19
1,48
1,28
а – коэффициент ширины венца колеса bа = b2 /аW :
для симметрично расположенной прямозубой и косозубой передачи относительно опор bа = 0,25 0,4,
для шевронной bа = 0,4 0,8;
в открытой передаче для шестерни, расположенной консольно относительно опор bа = 0,2 0,25 ;

4.

580,72 103
a 43 (5 1) 3
1,015 192,58 мм
0,3 52 434,72
Полученное значение межосевого расстояния округляют до ближайшего стандартного значения аW, мм:
200
Вычисляют модуль зацепления:
для закрытых передач при твердостях колес HB 350
при твердости колеса и шестерни
соответственно HB 350 и HRC > 45
при твердостях колес HRC 45
для открытых передач
m ' (0,01 0,02) aw
m ' (0,01 0,02) aw
m ' (0,016
0,0315) aw
2 K m T2 103
m
,
d 2 b2 F
Полученное значение модуля m округляют до стандартного m (мм) из ряда чисел:
3
m ' 0,015 200 3 мм

5.

В силовых зубчатых передачах при твердости колес 350 НВ принимаем m 1 мм;
при твердости одного из колес 45 HRC, принять m 1,5 мм.
В открытых зубчатых передачах расчетное значение модуля m увеличить на 30 % из-за повышенного
изнашивания зубьев.
Угол наклона зубьев для косозубых передач:
min
ширина венца колеса
Тогда
3,5 m
arcsin
b2
b2 = a aW = 0,3·200 = 60 мм .
min arcsin
3,5 3
10,0786
60
Для косозубых колес угол наклона зубьев должен находиться в диапазоне 8 16 ,
для шевронных - 25 40
Суммарное число зубьев шестерни и колеса.
z
2aw cos 2 200 cos(10,0786 )
131,28
m
3
131
Число зубьев шестерни
z
131
z1
21,83
изп 1 5 1
22
зуба
зуб

6.

Число зубьев колеса
z2 z z1 131 22 109
Вычисляют фактическое передаточное число иф и его отклонение и от заданного и:
иф
и
иф и
и
Z 2 109
4,95
Z1 22
100% 4%
4,95 5
и
100% 1% 4%.
5
Определяют действительную величину угла наклона зубьев для косозубых и шевронных передач
arсcos
Z m
131 3
arсcos
10,7348
2aW
2 200
Проверяют фактическое межосевое расстояние:
aW
z
z2 m
22 109 3
200 мм
2 cos
2 cos(10,7348 )
1

7.

Вычисляют основные геометрические параметры передачи для шестерни и колеса, мм:
Для колеса:
Для шестерни:
m z1
3 22
67,176 мм
cos cos(10,7348 )
m z2
3 109
d2
332,82 мм
cos cos(10,7348 )
d1
d a 2 d 2 2m 332,82 2 3 338,82 мм
d a1 d1 2m 67,176 2 3 73,176 мм
d f 1 d1 2,5m 332,82 2,5 3 325,32 мм
d f 1 d1 2,5m 67,176 2,5 3 59,676 мм
b1 b2 (2...5) 60 4 64 мм

8.

Проверочный расчет
Проверяем межосевое расстояние
d1 d2 67,176 332,82
aW
199,998 мм
2
2
Диаметр заготовки шестерни
Dзаг1 d a1 6 73,176 6 79,176 мм
Ширина заготовки шестерни
S заг1 b1 6 64 6 70 мм
Диаметр заготовки колеса
Ширина заготовки колеса
Dзаг 2 d a 2 6 338,82 6 344,82 мм
S заг 2 b2 6 60 6 66 мм

9.

Проверяем выполнение условия по контактной прочности H [ ]H
Н K
Ft (uф 1)
d1 b2 uф
K Н K Н K НV [ ]Н
где K – вспомогательный коэффициент,
для косозубых и шевронных передач K = 376
для прямозубых K = 436 ;
Ft – окружная сила в зацеплении, Н ;
2Tт 2 580,72 103
Ft
3489,6 Н
d2
332,82
KH коэффициент, учитывающий распределение нагрузки между зубьями.
для прямозубых KH = 1,
для косозубых и шевронных KH выбирается в зависимости от окружной
скорости колес V = 2 d2 / (2 103), м/с и степени точности передачи;
V
9,23 332,82
1,54 м с
3
2 10

10.

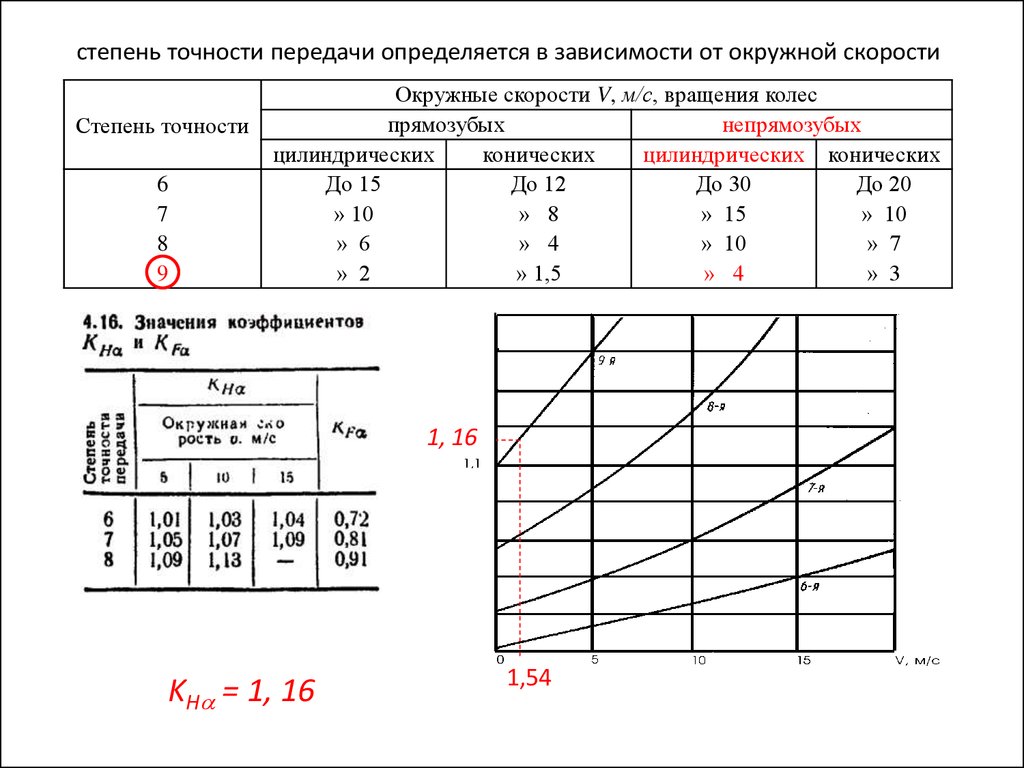
степень точности передачи определяется в зависимости от окружной скорости
Степень точности
6
7
8
9
Окружные скорости V, м/с, вращения колес
прямозубых
непрямозубых
цилиндрических
конических
цилиндрических конических
До 15
До 12
До 30
До 20
» 10
» 8
» 15
» 10
» 6
» 4
» 10
» 7
» 2
» 1,5
» 4
» 3
1, 16
KH = 1, 16
1,54

11.

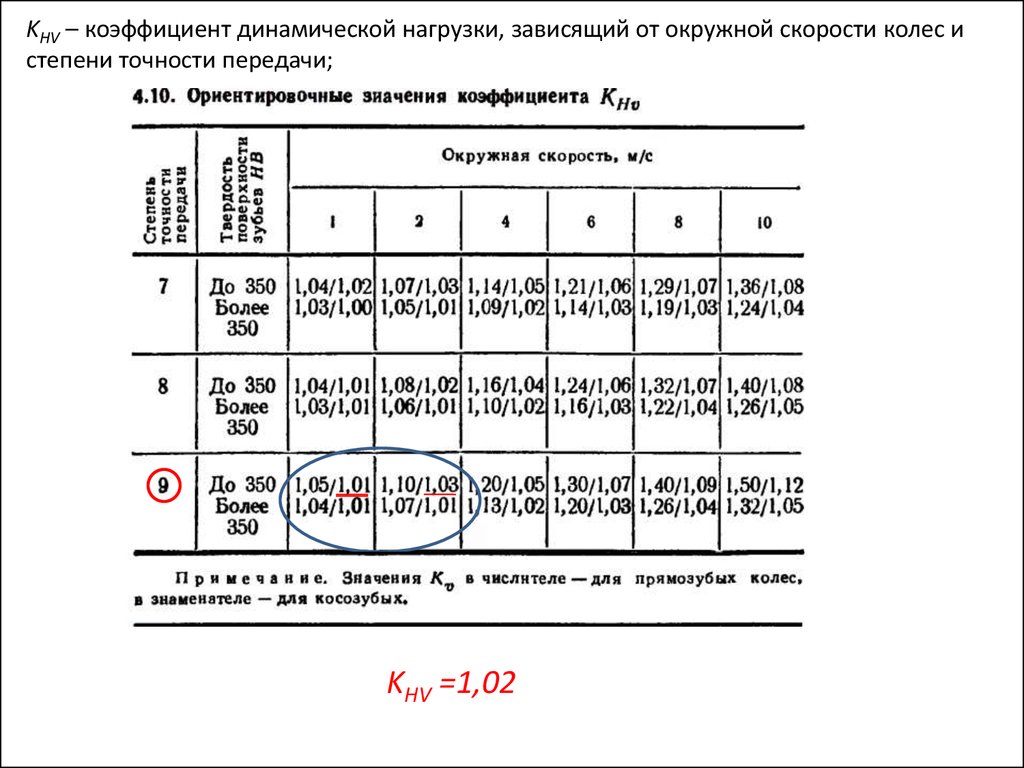
KHV – коэффициент динамической нагрузки, зависящий от окружной скорости колес и
степени точности передачи;
KHV =1,02

12.

3489,6 (4,95 1)
Н 376
1,16 1,015 1,02 420,35 МПа [ ]Н
67,176 60 4,95
420,35 МПа < 434,7 МПа
Далее проверяем выполнение условия изгибной прочности зубьев
шестерни и колеса
F 2
Ft
YF 2 Y
KF KF KFV F 2 ;
b2m
F 1 F 2 YF 1 / YF 2 F 1 ,
KF коэффициент, учитывающий распределение нагрузки между зубьями.
для прямозубых KF = 1,
для косозубых и шевронных KF зависит от степени точности передачи,
определяемой по таблице.
Степень точности
6
7
8
9
Коэффициент KF
0,72
0,81
0,91
1,0

13.

KF – коэффициент неравномерности нагрузки по длине зуба.
Для прирабатывающихся зубьев KF = 1,
для зубьев с твердостью > 350НВ KF определяется по табл.
KF = 1,02

14.

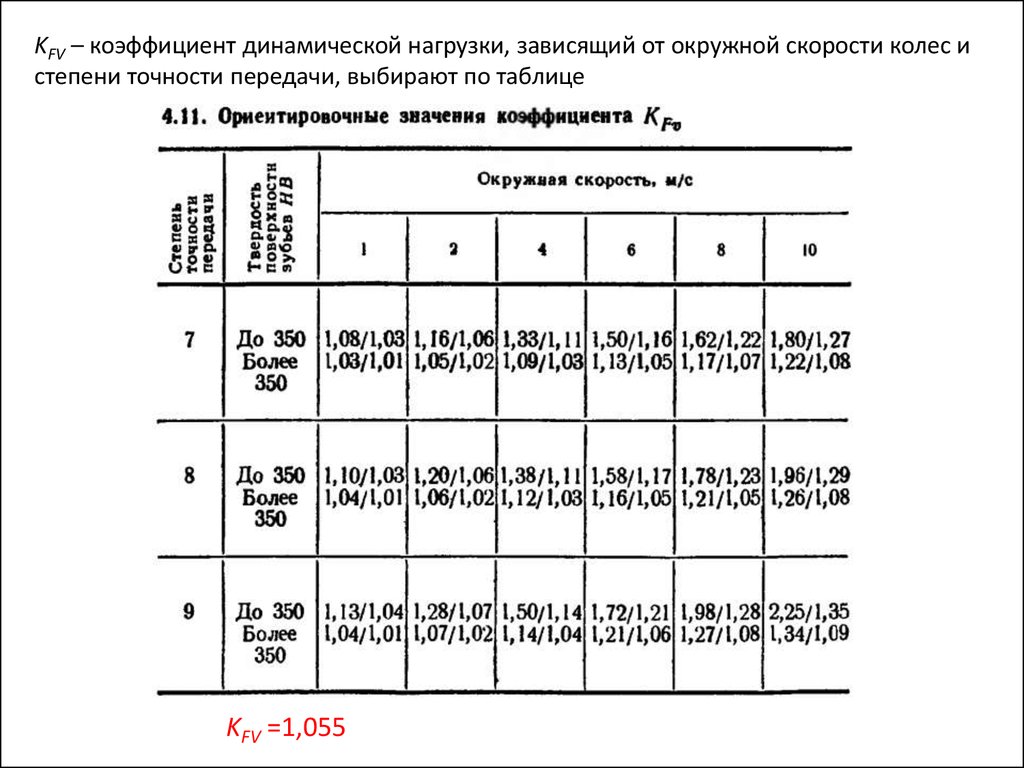
KFV – коэффициент динамической нагрузки, зависящий от окружной скорости колес и
степени точности передачи, выбирают по таблице
KFV =1,055

15.

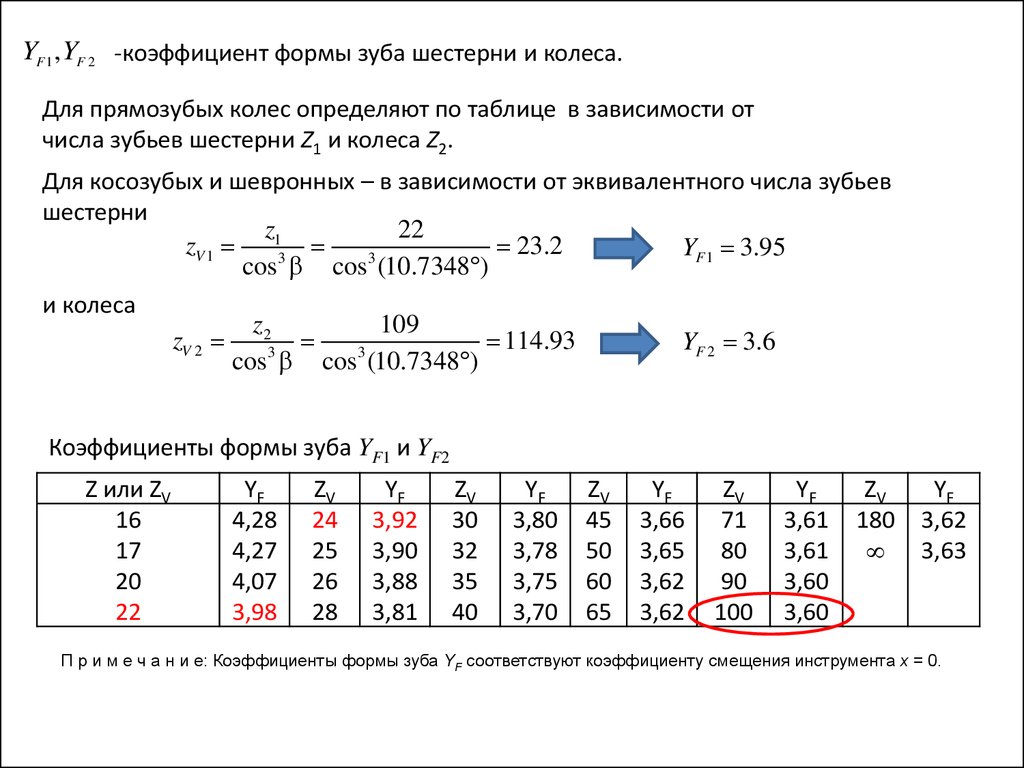
YF 1 , YF 2 -коэффициент формы зуба шестерни и колеса.
Для прямозубых колес определяют по таблице в зависимости от
числа зубьев шестерни Z1 и колеса Z2.
Для косозубых и шевронных – в зависимости от эквивалентного числа зубьев
шестерни
z
22
zV 1 13
23.2
YF 1 3.95
3
cos cos (10.7348 )
и колеса
zV 2
z2
109
114.93
cos3 cos3 (10.7348 )
YF 2 3.6
Коэффициенты формы зуба YF1 и YF2
Z или ZV
16
17
20
22
YF
4,28
4,27
4,07
3,98
ZV
24
25
26
28
YF
3,92
3,90
3,88
3,81
ZV
30
32
35
40
YF
3,80
3,78
3,75
3,70
ZV
45
50
60
65
YF
3,66
3,65
3,62
3,62
ZV
71
80
90
100
YF
3,61
3,61
3,60
3,60
ZV
180
YF
3,62
3,63
П р и м е ч а н и е: Коэффициенты формы зуба YF соответствуют коэффициенту смещения инструмента x = 0.

16.

Y – коэффициент, учитывающий наклон зуба,
для прямозубых колес Y =1
для косозубых
Y 1
10.7348
1
0.92
140
140
Выполним подстановку значений
3489.6
F 2 3.95 0.92
1 1.02 1.055 71.1 F 2 188 МПа
64 3
3.95
F 1 77.1
77.98 F 1 211 МПа
3.6