Похожие презентации:
Дифференциальное уравнение изогнутой оси упругого стержня и его интегрирование
1.
Дифференциальное уравнениеизогнутой оси упругого стержня и
его интегрирование
2.
Прогибы и углы поворота сечений|x=l = y’ |x=l
B1
y
F
C1
y|x=l
y
X
C
A
B
y=y(x)
X
l
Рис. 1.
= (x)
≈tg( ) ≈dy/dx
3.
Метод непосредственного интегрированиядифференциального уравнения упругой линии
(Изгиб стержней (нормальные напряжения) (14))
1/ρ=MZ/EIZ
1/ρ=MZ(x)/EIZ
(1)
(2)
(3)
(5)
EIZyII = ±MZ(x)
(6)
дифференциальное
уравнение упругой
линии
приближенное
дифференциальное
уравнение упругой
линии
4.
EIZyII = MZ(x)1/ρ ≈ yII > 0
1/ρ ≈ yII < 0
EIZyII = MZ(x)
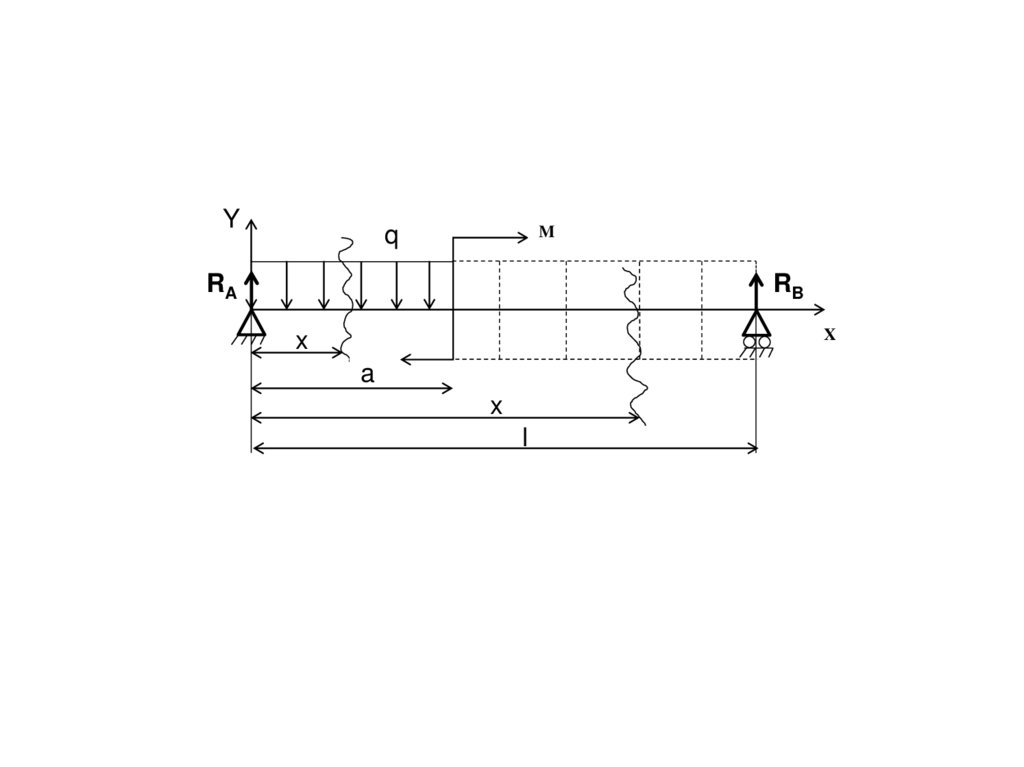
5.
Yq
M
RA
RB
X
xx
aa
x
l
6.
(7)(8)
(9)
1 й участок
2 й участок
a
(10)
(14)
(11)
(15)
(12)
(16)
6
RA
x3
(13)
2
(17)
7.
Граничные условия(18)
(19)
(20)
(21)
(22)
(23)
Два участка, два дифференциальных уравнения, четыре постоянных
интегрирования. Для балки, содержащей n участков – 2n постоянных.
Существует метод, позволяющий получить:
C1 = C2 = ... = Cn = C
D1 = D2 = ... = Dn = D
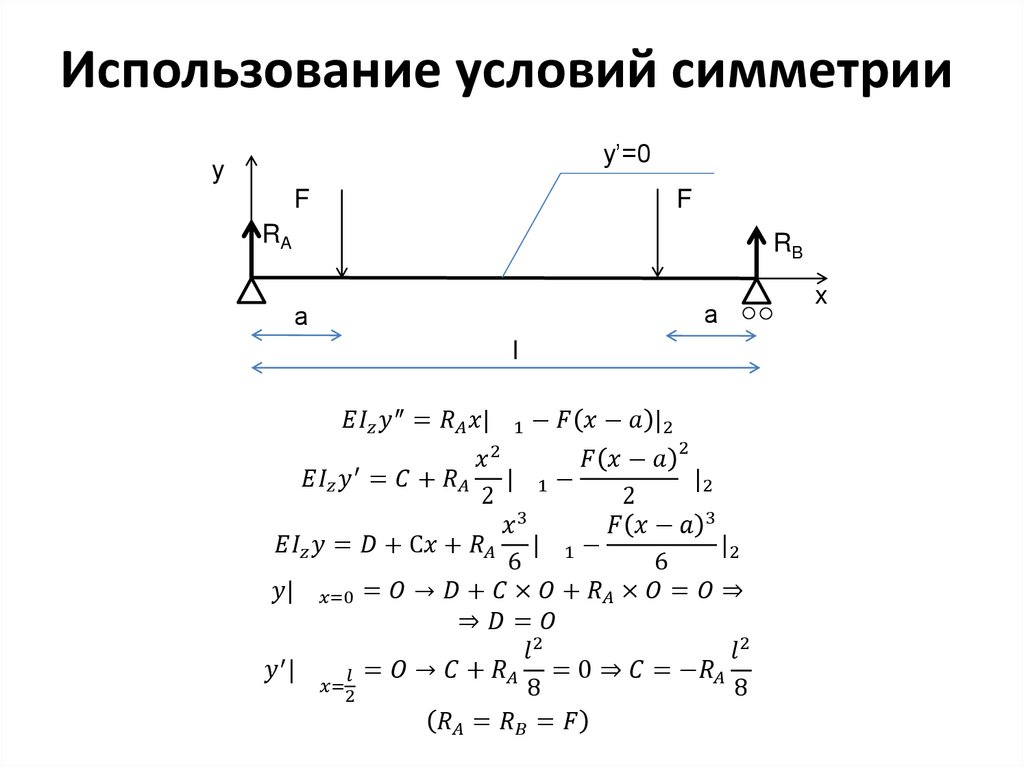
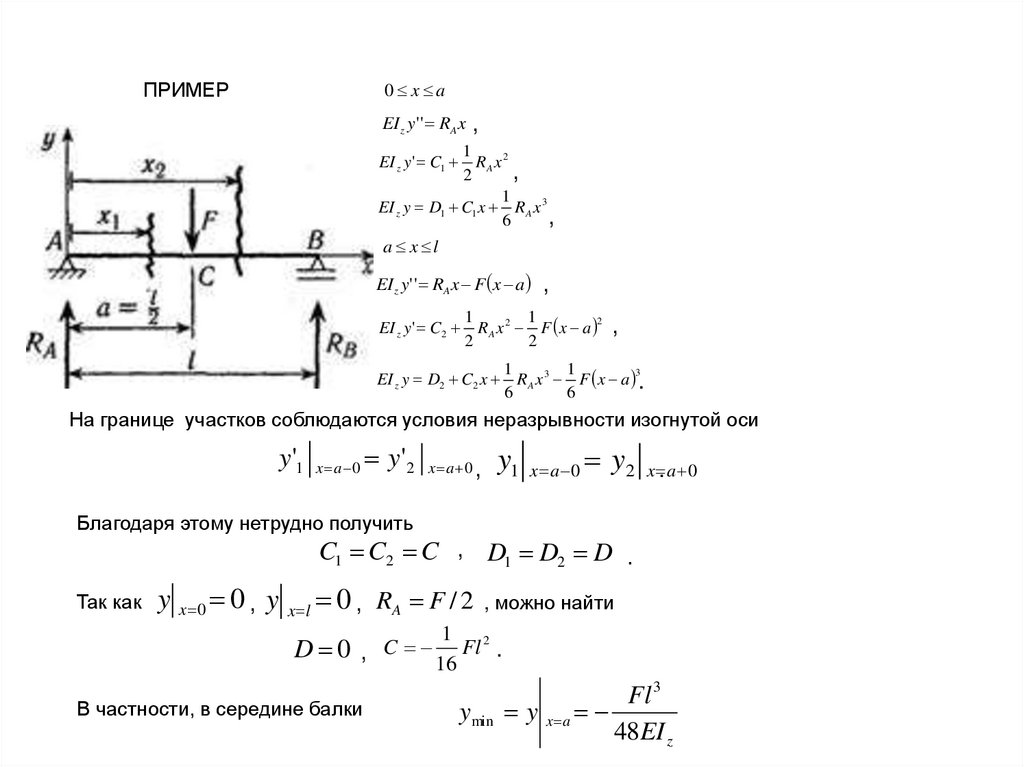
8.
Метод уравнивания постоянныхинтегрирования
1. Начало координат - единое для всех участков балки,
расположено на одном из её концов.
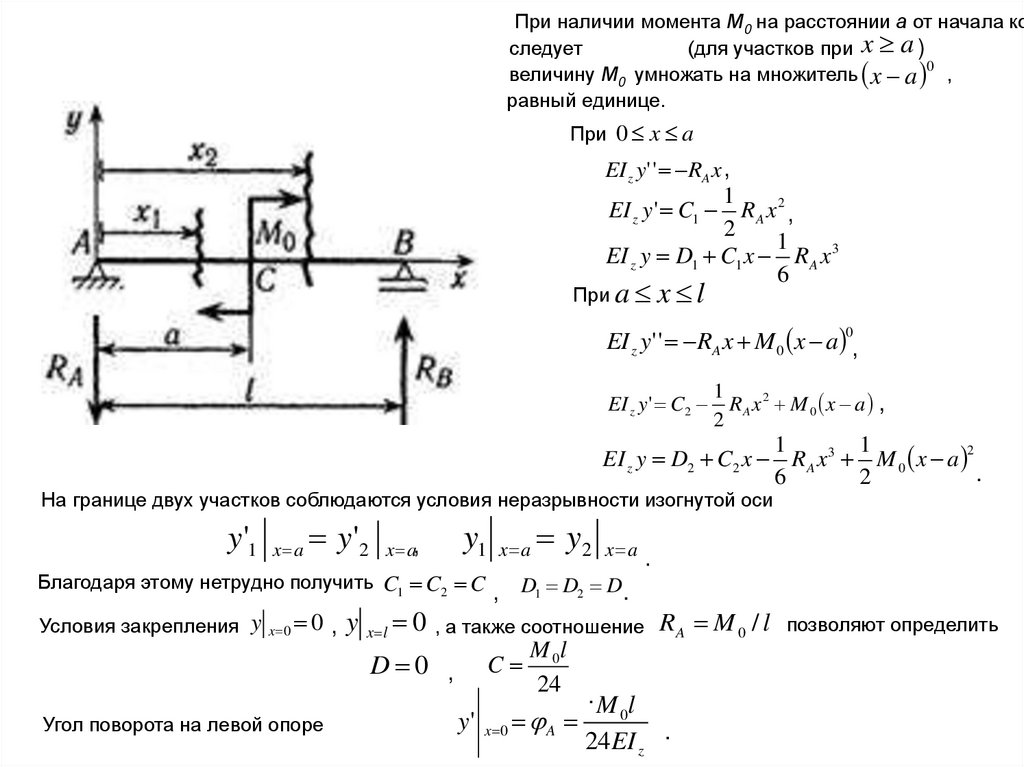
2. При составлении формулы изгибающего момента
следует двигаться от начала координат. Формула
изгибающего момента участка содержит все слагаемые
изгибающего момента на предыдущих участках. Все
слагаемые имеют множитель (x - а) в соответствующей
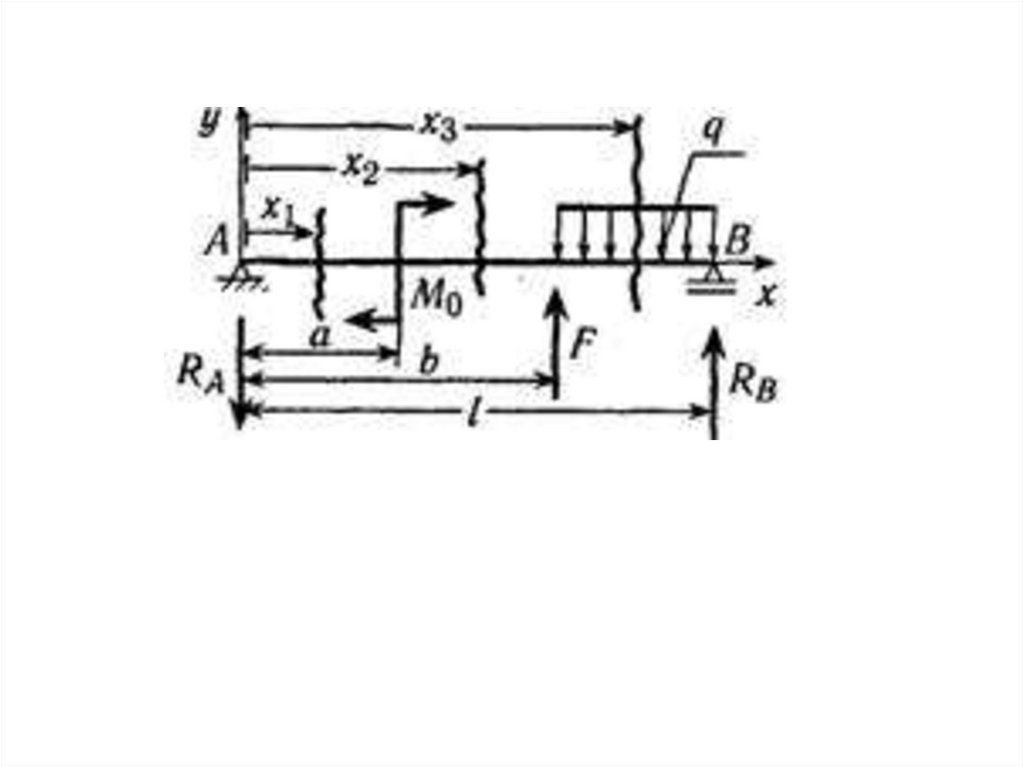
степени. Если участок содержит распределенную
нагрузку, то она продлевается до конца балки и, начиная
со следующего участка, вводится компенсирующая
распределенная нагрузка.
3. Интегрирование производится без раскрытия скобок.
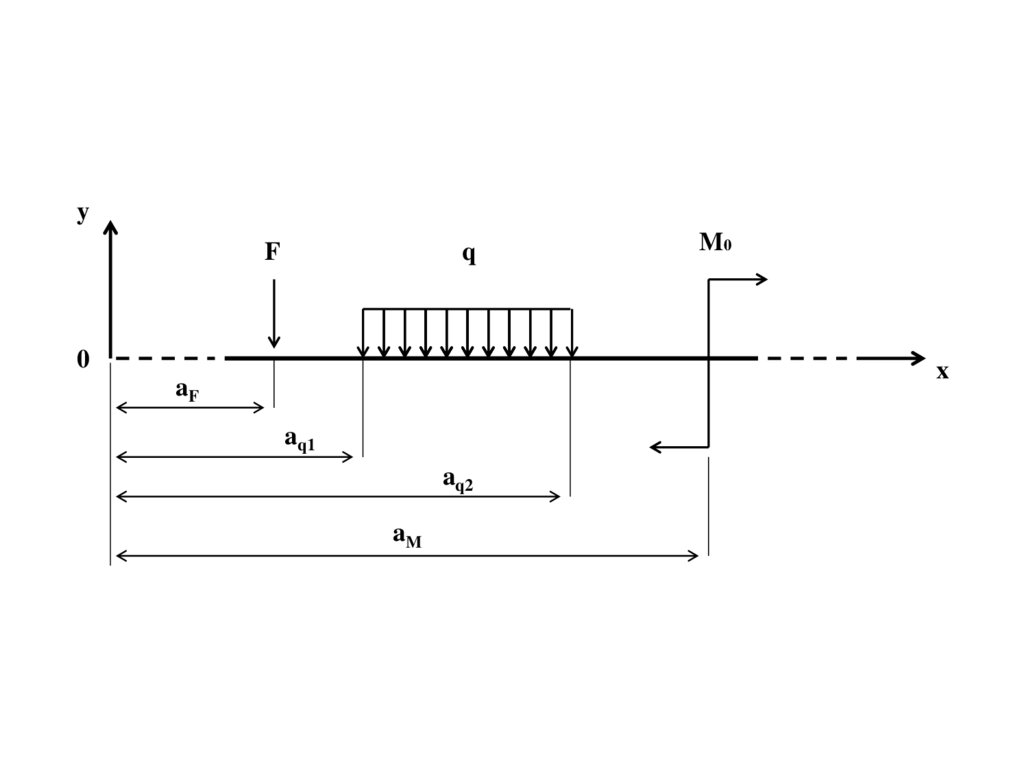
9.
yF
q
0
M0
x
aF
aq1
aq2
aM
10.
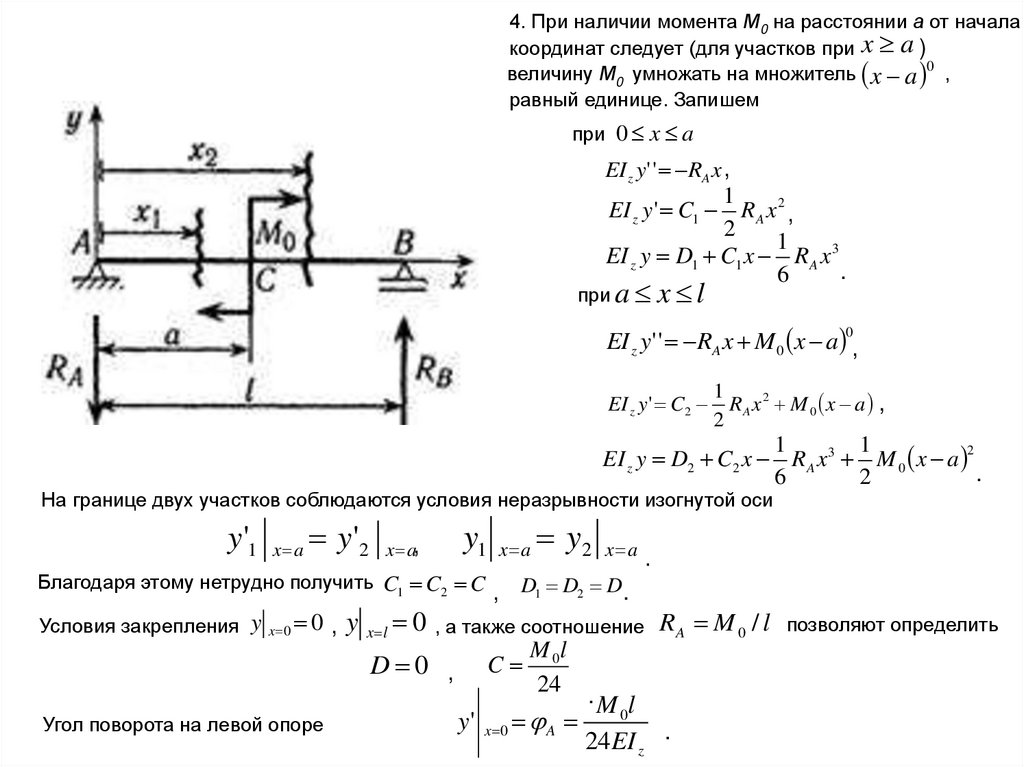
(18)(19)










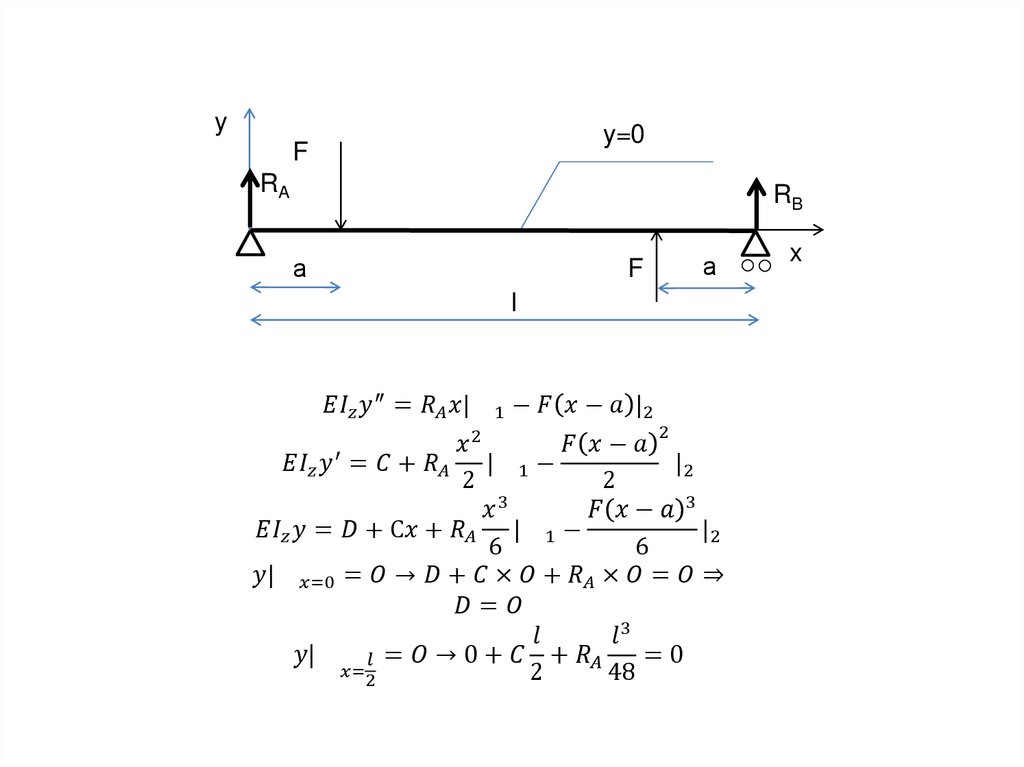





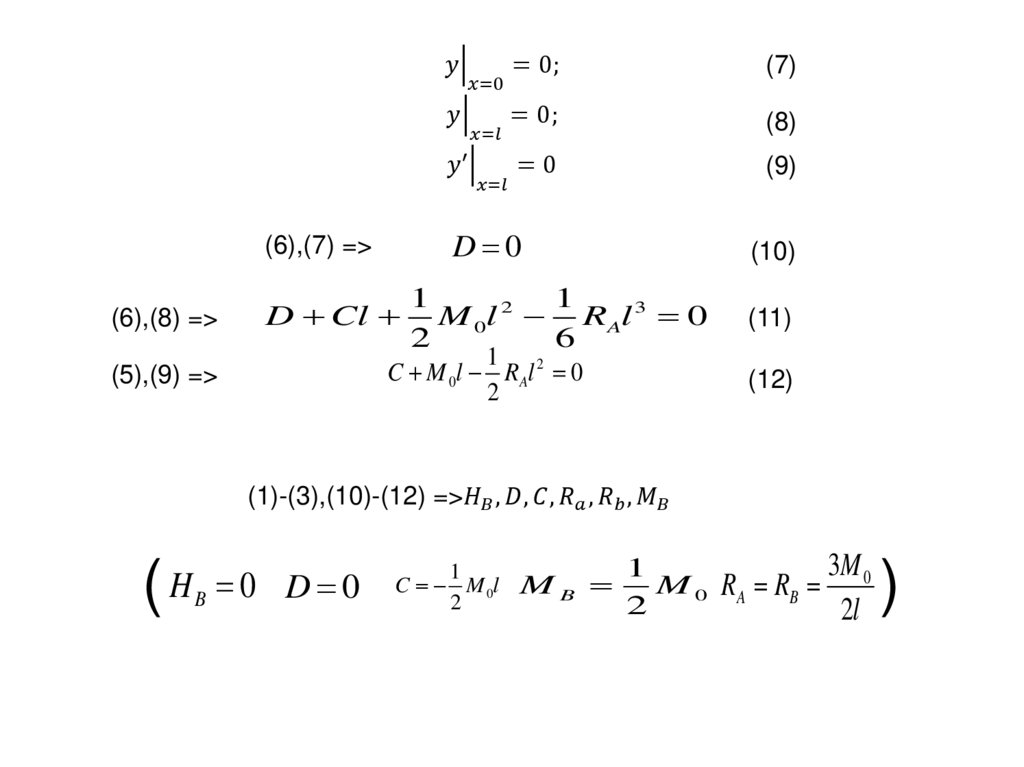











 Механика
Механика








