Похожие презентации:
Задача лінійного програмування та методи її розв’язування(Лекція 3)
1. ЛЕКЦІЯ 3 ЗАДАЧА ЛІНІЙНОГО ПРОГРАМУВАННЯ ТА МЕТОДИ ЇЇ РОЗВ’ЯЗУВАННЯ
2. План
3.1 Загальна економіко-математичнамодель задачі лінійного
програмування.
3.2 Форми запису задач лінійного
програмування.
3.3 Геометрична інтерпретація задачі
лінійного програмування.
3.4 Основні властивості розв’язків задачі
лінійного програмування.
3.5 Графічний метод розв’язування задач
лінійного програмування.
3. Загальна економіко-математична модель задачі лінійного програмування
max (min) Z c1 x1 c 2 x 2 c n x n (3.1)a11 x1 a12 x 2 a1n x n , , b1 ;
a x a x a x , , b ; (3.2)
21 1
22 2
2n n
2
............................................................
a m1 x1 a m 2 x 2 a mn x n , , bm .
x1 0, x 2 0, , x n 0.
(3.3)
4.
Допустимий розв’язок (план) задачілінійного програмування
Х = (х1, х2, …, хn)
Оптимальний розв’язок (план) задачі
лінійного програмування
X * ( x1* , x2* , , xn* )
5.
аi1х1+аi2х2+…+аinxn ≤ bibi (i = 1, 2, …, m)
ai1x1+ai2x2+…+ ain xn + xn + 1 = bi
аk1x1 + ak2x2 + … + aknxn ≥ bk
ak1x1 + ak2x2 + … + aknxn – xn + 2 = bk
(хn+1 ≥ 0, хn+2 ≥ 0)
6. Форми запису задач лінійного програмування
nmax(min) Z c j x j
j 1
n
aij x j bi (i 1, 2, , m);
j 1
x j 0 ( j 1, 2, , n).
(3.4)
7.
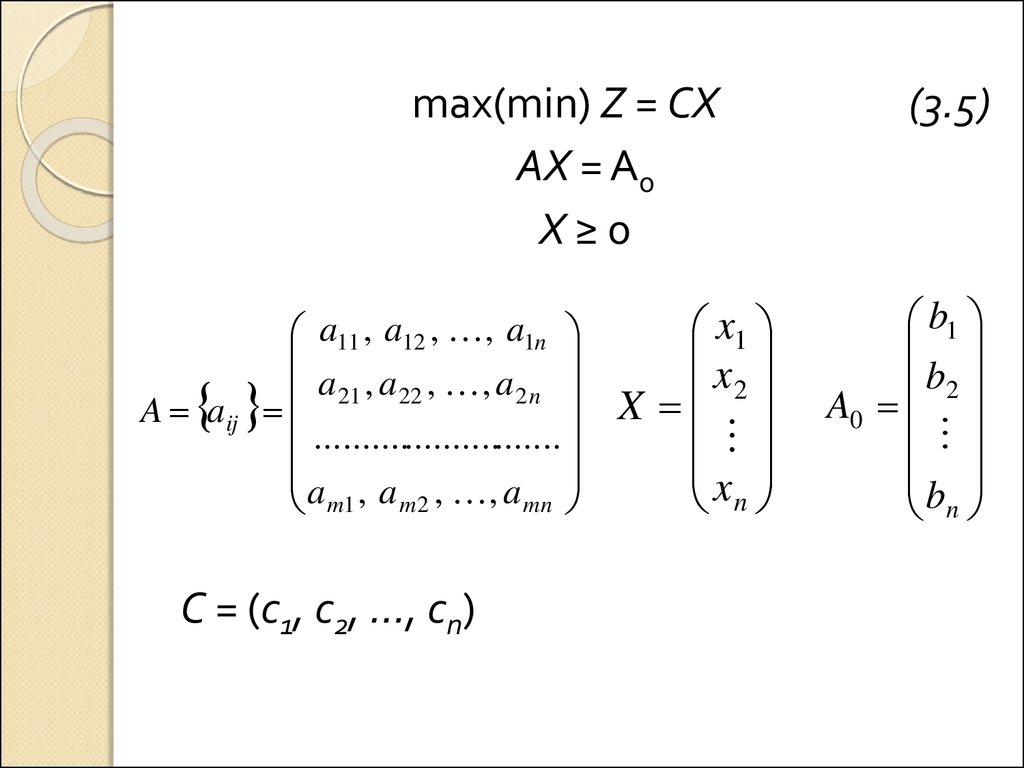
max(min) Z = CXАХ = А0
Х≥0
a11 , a12 , , a1n
a 21 , a 22 , , a 2 n
A a ij
...........................
a m1 , a m 2 , , a mn
С = (с1, с2, …, сп)
x1
x
X 2
x
n
(3.5)
b1
b2
A0
bn
8.
max(min)Z = CXA1x1 + A2x2 + … + Anxn = A0
(3.6)
a11
a12
a1n
a 21
a 22
a 2n
A1
, A2
, , An
a
a
a
m1
m2
mn
9. Геометрична інтерпретація задачі лінійного програмування
х1Оx2a11 x1 a12 x 2 b1 ;
a x a x b ;
21 1
22 2
2
..............................
a m1 x1 a m 2 x 2 bm .
x1 0, x 2 0.
ai1x1 + ai2x2 = bi (i=1,2, ..., т)
(3.7)
10.
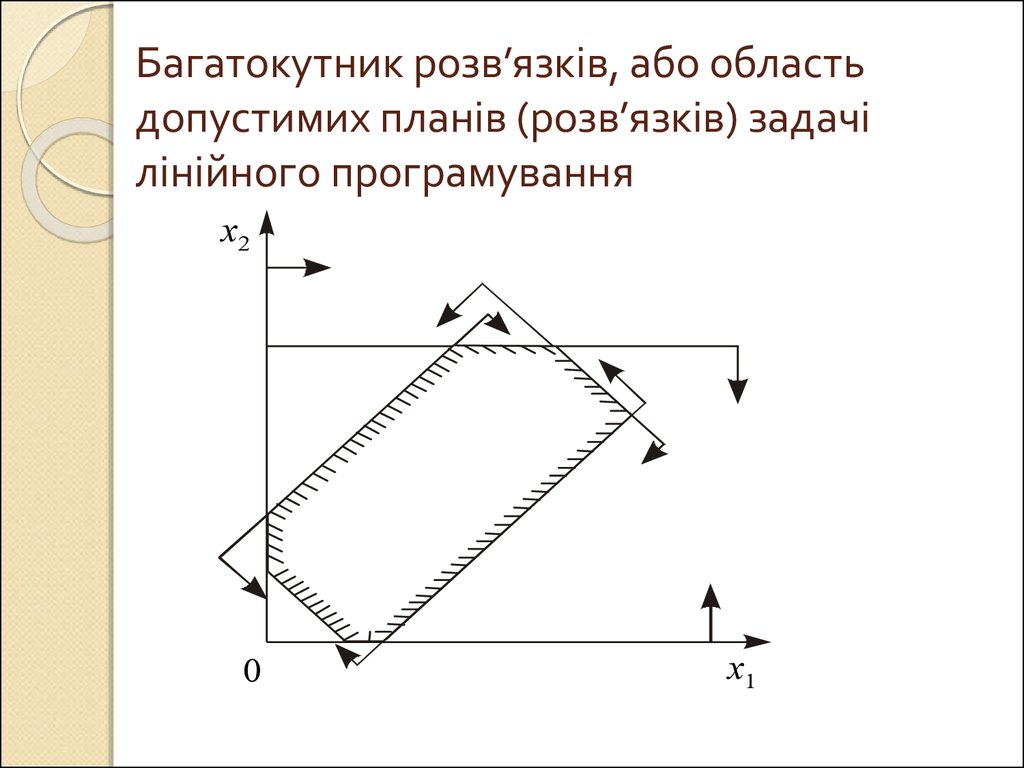
Багатокутник розв’язків, або областьдопустимих планів (розв’язків) задачі
лінійного програмування
x2
0
x1
11.
ai1x1 + ai2x2 + ai3x3 = bi (i = 1, 2, ..., т)хj=0 (j = 1, 2, 3)
х1, х2,… хn
аi1x1 + ai2x2 + ai3x3 + … +ainxn = bi
(i = 1, 2, ..., т)
хj = 0 (j=1, 2, 3, ..., n)
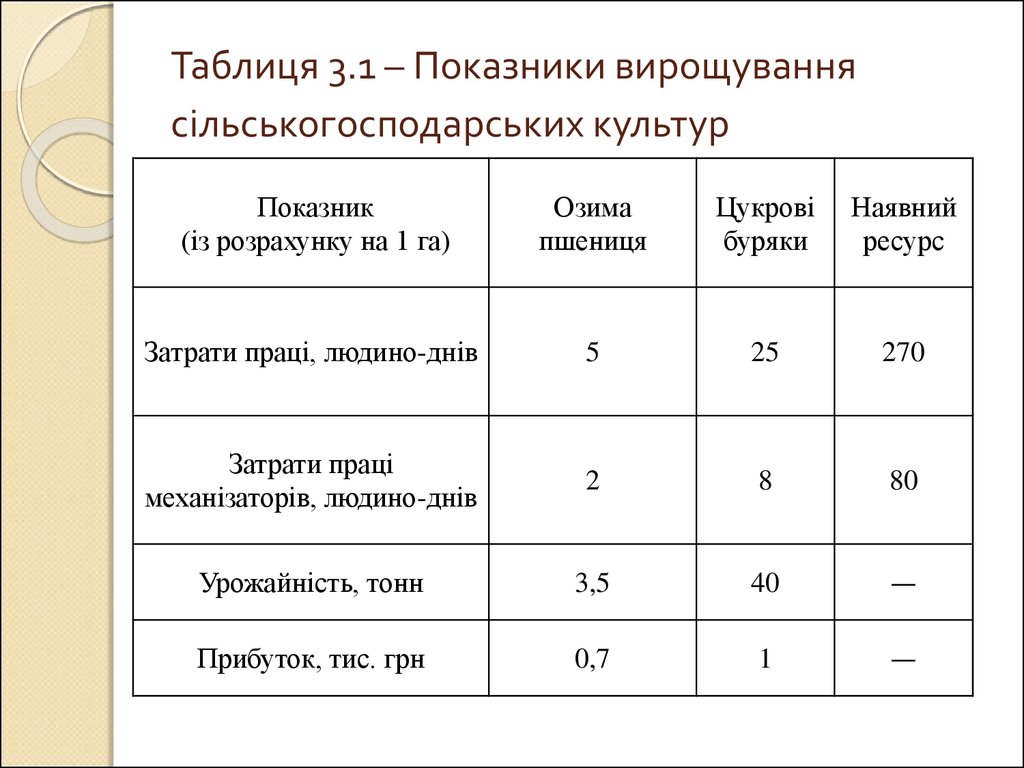
12. Таблиця 3.1 – Показники вирощування сільськогосподарських культур
Показник(із розрахунку на 1 га)
Озима
пшениця
Цукрові
буряки
Наявний
ресурс
Затрати праці, людино-днів
5
25
270
Затрати праці
механізаторів, людино-днів
2
8
80
Урожайність, тонн
3,5
40
—
Прибуток, тис. грн
0,7
1
—
13.
Задача лінійного програмування маєтакий вигляд:
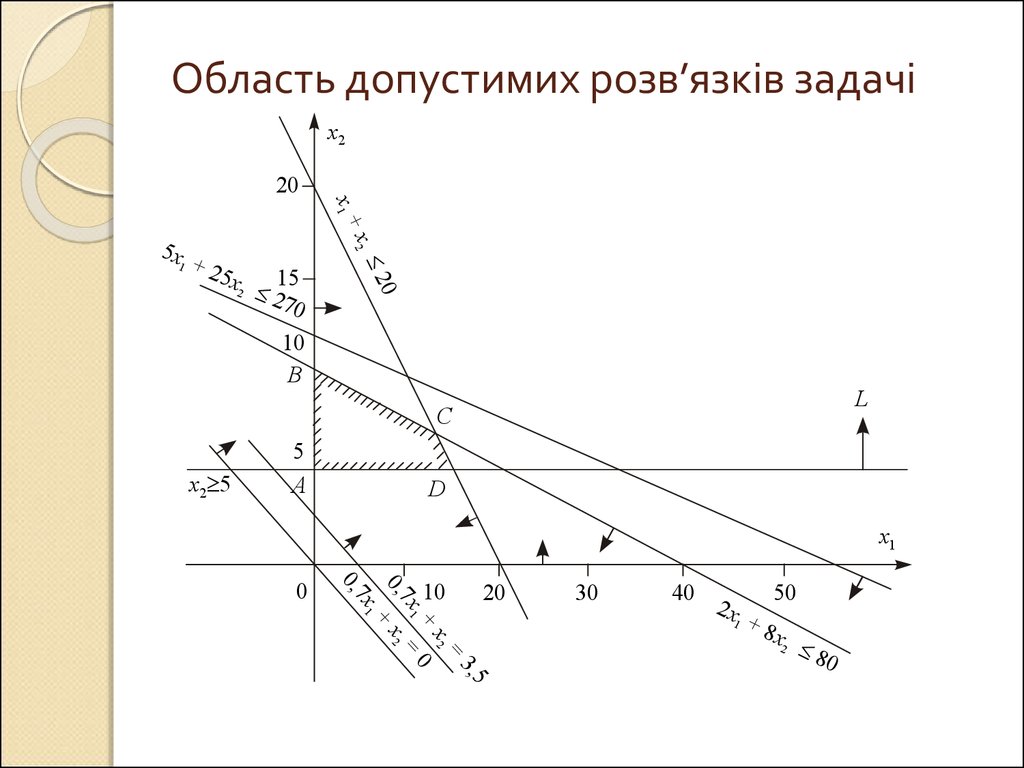
max Z = 0,7x1 + x2
(3.8)
за умов:
x1 + x2 ≤ 20;
(3.9)
5x1 + 25x2 ≤ 270;
(3.10)
2x1 + 8x2 ≤ 80;
(3.11)
x2 ≥ 5;
(3.12)
x1 ≥ 0, x2 ≥ 0.
(3.13)
14. Область допустимих розв’язків задачі
x220
x1+
215
70
0
2
2
25x
x2
5x
1 +
10
B
L
C
x2
5
A
D
x1
10
20
1
3,5
=
x2
+
x1 = 0
0,7 + x 2
x
0,7
0
30
40
2x
1
50
+8
x2
8
0
15. Основні властивості розв’язків задачі лінійного програмування
Властивість 1. (Теорема 3.1) Множина всіхпланів задачі лінійного програмування
опукла.
Властивість 2. (Теорема 3.2) Якщо задача
лінійного програмування має оптимальний
план, то екстремального значення цільова
функція набуває в одній із вершин її
багатогранника розв’язків. Якщо ж цільова
функція набуває екстремального значення
більш як в одній вершині цього
багатогранника, то вона досягає його і в
будь-якій точці, що є лінійною комбінацією
таких вершин.
16.
Властивість 3. (Теорема 3.3) Якщо відомо, щосистема векторів A1, A2, …, Ak (k≤n) у розкладі
A1x1 +A2x2 + … + Anxn = A0, X≥0 лінійно
незалежна і така, що
A1x1 + A2x2 + … + Akxk = A0,
де всі xj ≥ 0, то точка X = (x1, x2, …, xk, 0, …, 0) є
кутовою точкою багатогранника розв’язків.
Властивість 4. (Теорема 3.4) Якщо X = (x1, x2,
…, xn) – кутова точка багатогранника
розв’язків, то вектори в розкладі
A1x1 + A2x2 + … + Anxn = A0, X ≥ 0,
що відповідають додатним xj, є лінійно
незалежними.
17. Графічний метод розв’язування задач лінійного програмування
max(min) Z c1 x1 c 2 x 2a11 x1 a12 x 2 { , , }b1 ;
a x a x { , , }b ;
22 2
2
21 1
a 31 x1 a 32 x 2 { , , }b3 ;
a m1 x1 a m 2 x 2 { , , }bm .
x1 0, x 2 0
a i1 x1 a i 2 x 2 bi
(і = 1, 2, …, т)
(3.15)
(3.16)
(3.17)
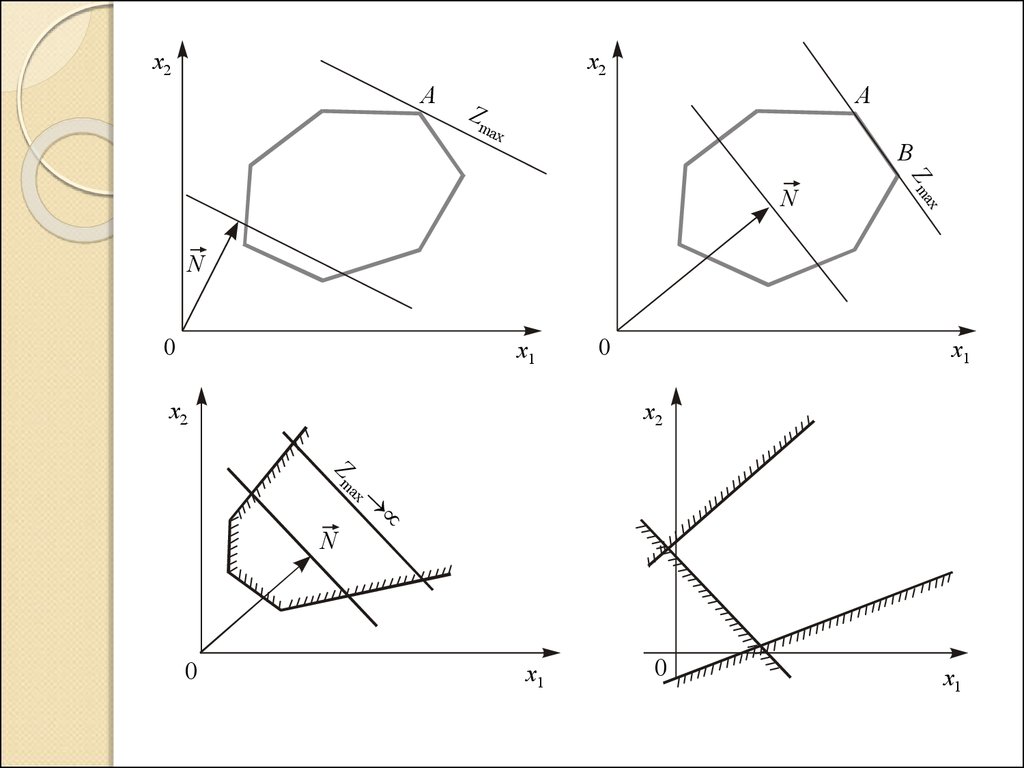
18. Алгоритм графічного методу
1. Будуємо прямі, рівняння яких дістаємозаміною в обмеженнях задачі (3.16) знаків
нерівностей на знаки рівностей.
2. Визначаємо півплощини, що відповідають
кожному обмеженню задачі.
3. Знаходимо багатокутник розв’язків задачі
лінійного програмування.
4. Будуємо вектор N (c1 ; c2 ) , що задає
напрям зростання значення цільової функції
задачі.
19.
5. Будуємо пряму с1х1+с2х2=const,перпендикулярну до вектора .
6. Рухаючи пряму с1х1+с2х2=const в напрямку
вектора
(для задачі максимізації) або в
протилежному напрямі
(для задачі мінімізації), знаходимо вершину
багатокутника розв’язків, де цільова функція
набирає екстремального значення.
7. Визначаємо координати точки, в якій
цільова функція набирає максимального
(мінімального) значення, і обчислюємо
екстремальне значення цільової функції в
цій точці.
20.
x2x2
A
A
Zm
ax
B
x
Z ma
N
N
N
0
x1
x2
0
x1
x2
Z
m
ax
N
0
x1
0
x1
21.
x2Zm
ax
x2
B
N
N
0
min
Z
A
0
x1
x2
in
m
Z
N
ax
m
Z
0
x1
x1
22.
m n 2x3 31 x1 32 x 2 3 ;
x x x ;
4
41 1
42 2
4
...................................
x n n1 x1 n 2 x 2 n .
x i 0 (i 1, n)
x1 0, x 2 0
x3 31 x1 32 x 2 3 0;
x x x 0;
4
41 1
42 2
4
...................................
x n n1 x1 n 2 x 2 n 0.
(3.18)
23.
F c1 x1 c 2 x 2 ... c n x nF 0 1 x1 2 x 2
F 1 x1 2 x 2






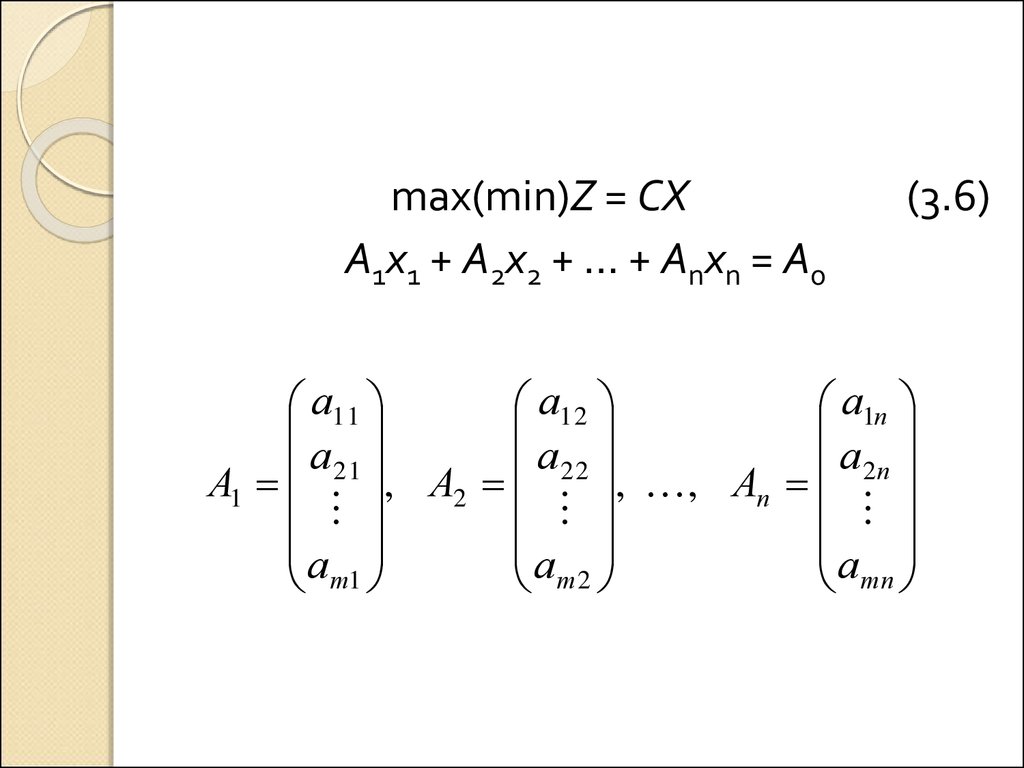










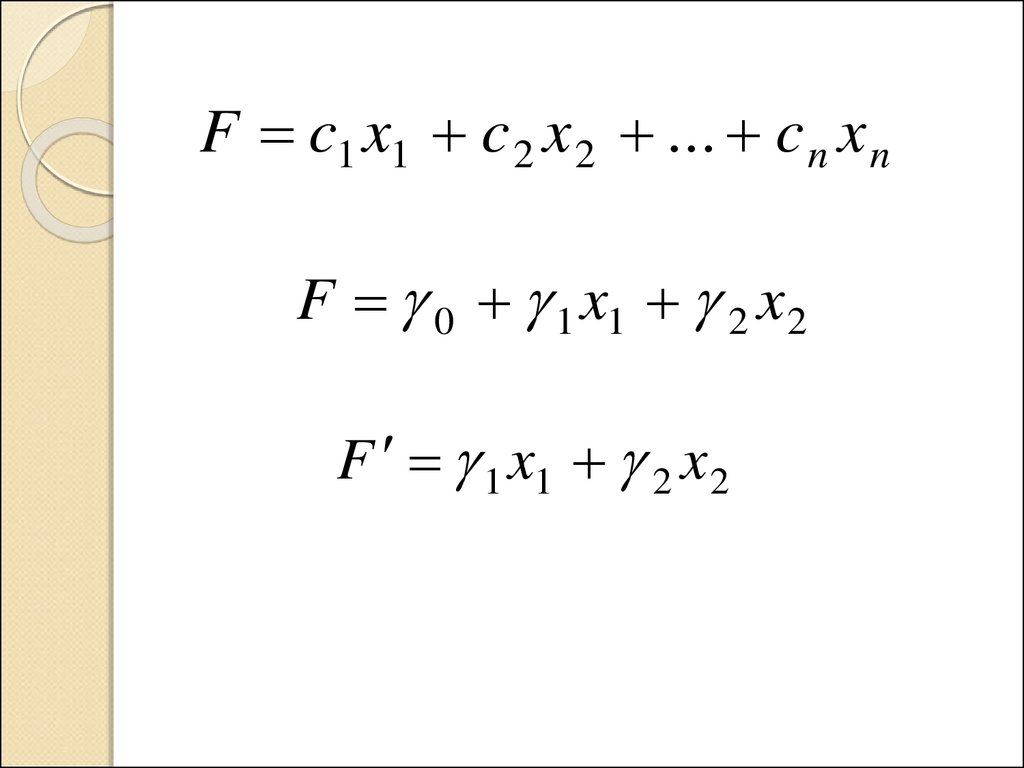
 Математика
Математика Программирование
Программирование








