Планарные графы

1. Планарные графы

Лекция 8

2. Географические карты

Политическая
карта
Физическая
карта
Толчком, ускорившим развитие теории
графов, явилась эпоха великих
географических открытий.

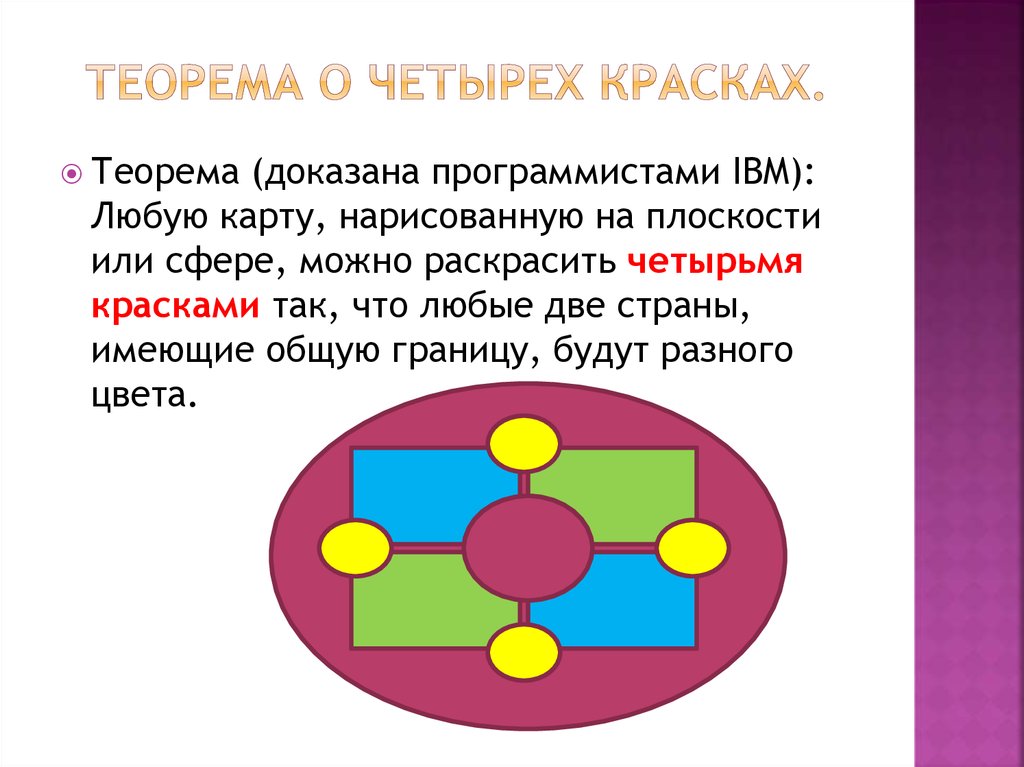
3. Теорема о четырех красках.

Теорема
(доказана программистами IBM):
Любую карту, нарисованную на плоскости
или сфере, можно раскрасить четырьмя
красками так, что любые две страны,
имеющие общую границу, будут разного
цвета.

4. тор

Теорема
2: Любую карту, нарисованную на
торе, можно раскрасить пятью красками
так, что любые две страны, имеющие
общую границу, будут разного цвета.

5. крендель

Теорема
3: Любую карту, нарисованную на
поверхности кренделя, можно раскрасить
шестью красками так, что любые две
страны, имеющие общую границу, будут
разного цвета.

6. топология

В
топологии считается, что все тела
сделаны из эластичного материала, и
потому их можно сжимать и растягивать
и они не порвутся. Такие деформации
зовутся гомеоморфизмом.
Т.о.
топология изучает свойства
гомеоморфных тел.

7. Определение планарного графа

Граф,
изображенный на
плоскости или на шаре,
называется плоским или
планарным графом, если его
ребра (дуги) не пересекаются
в точках, отличных от вершин
графа.

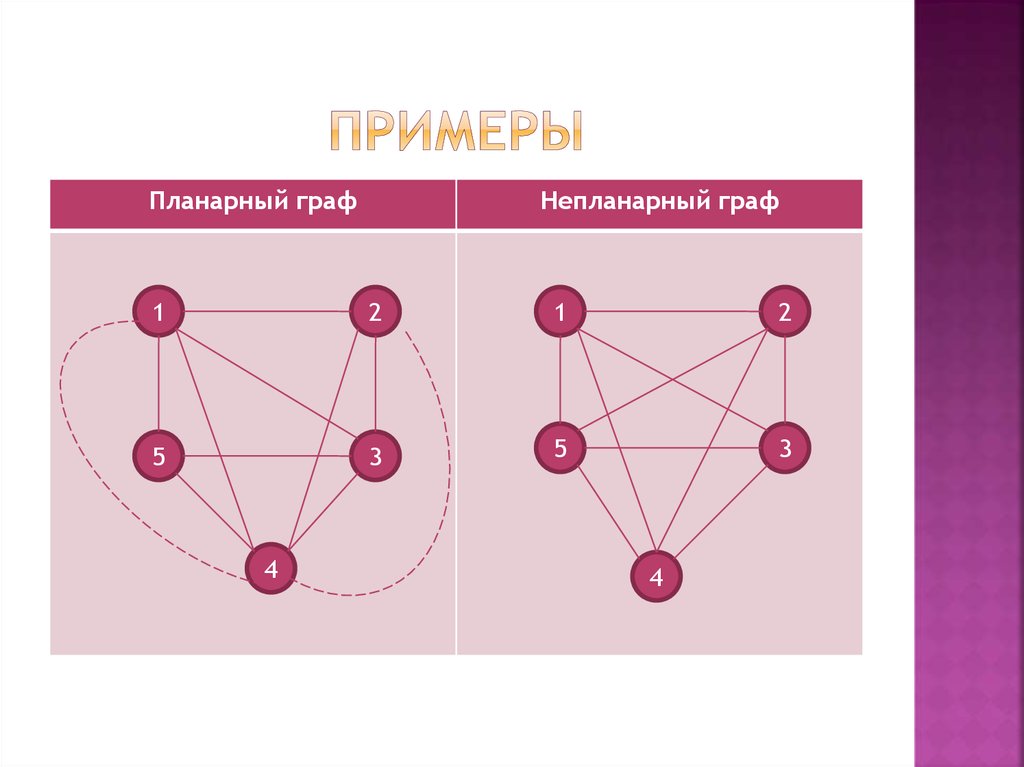
8. ПРИМЕРЫ

Планарный граф
Непланарный граф
1
2
1
2
5
3
5
3
4
4

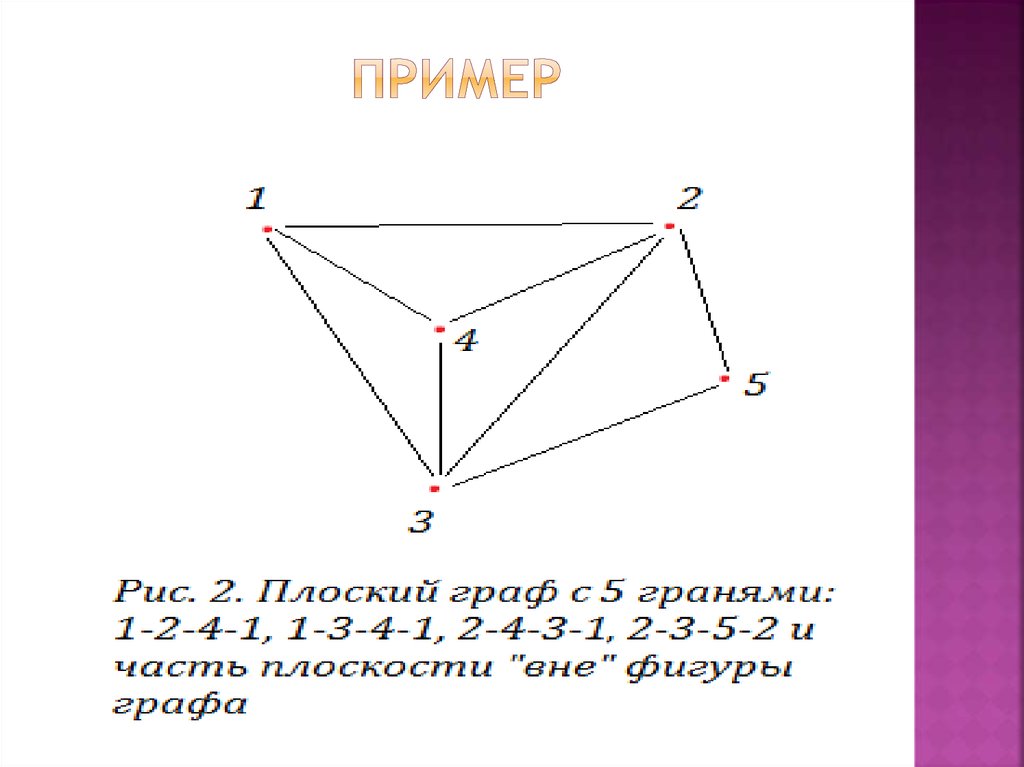
9. Что такое «грань»

Гранью (страной) в
плоском представлении
графа называется часть
плоскости, ограниченная
простым циклом и не
содержащая внутри
других циклов.

10. пример

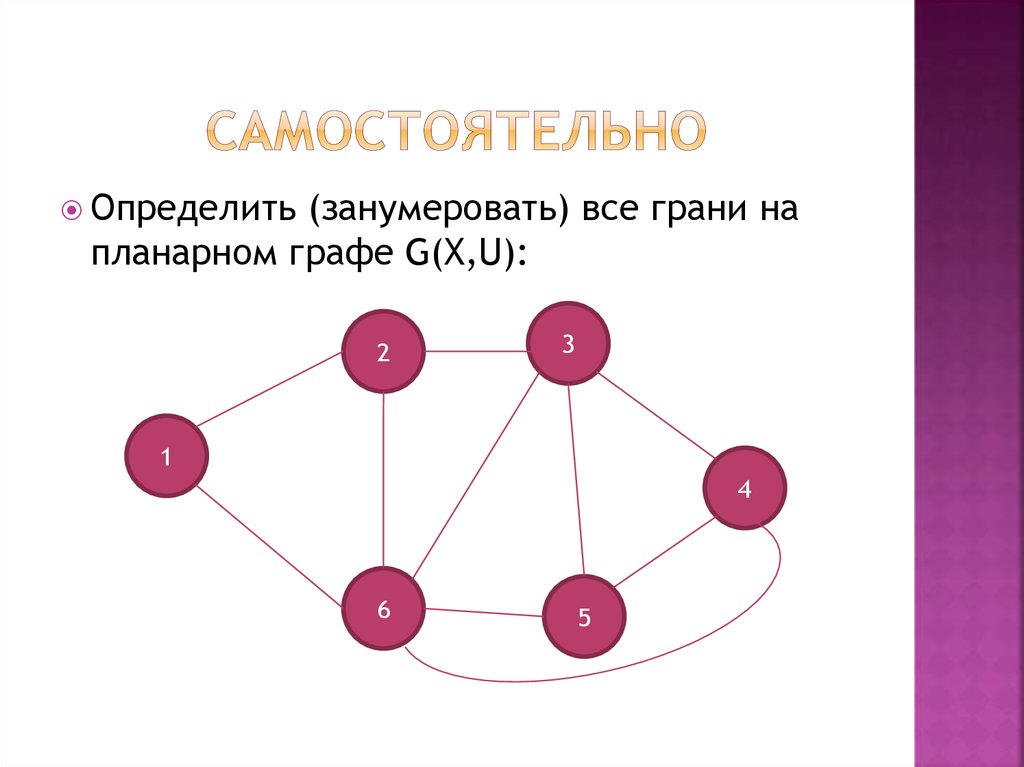
11. самостоятельно

Определить
(занумеровать) все грани на
планарном графе G(X,U):
2
3
1
4
6
5

12. Теорема эйлера

Пусть
В - количество вершин в
графе, Г - количество граней в
плоском представлении графа, Р количество рёбер в графе. Тогда
получаем формулу Эйлера для
связного планарного графа:
В+Г-Р=2

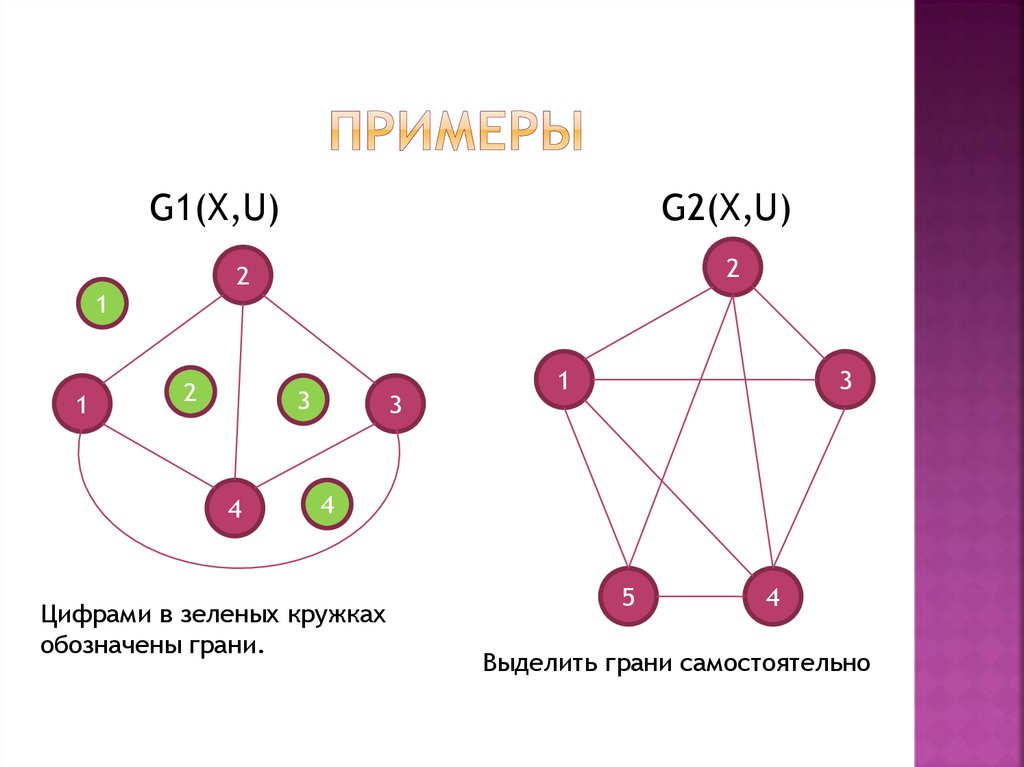
13. Примеры

G1(X,U)
2
2
1
1
G2(X,U)
2
3
4
3
1
3
4
Цифрами в зеленых кружках
обозначены грани.
5
4
Выделить грани самостоятельно

14. Формула эйлера для несвязного графа

Для несвязного
планарного графа с K
компонентами связности
формула Эйлера имеет
вид:
В + Г - Р = K + 1.

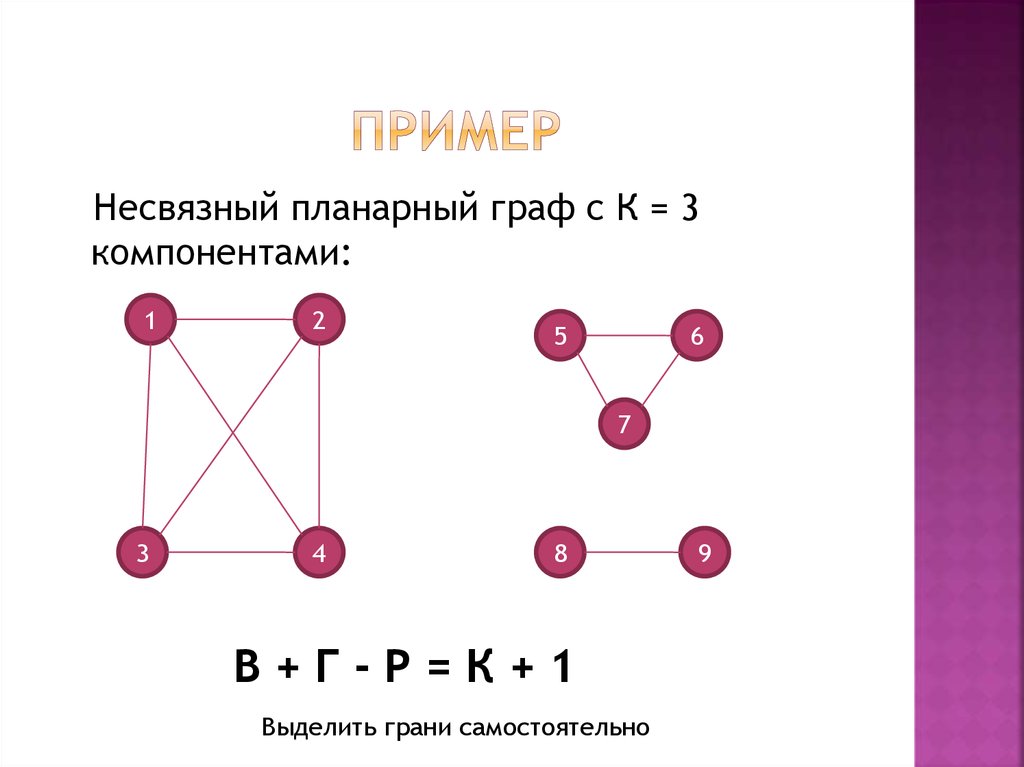
15. пример

Несвязный планарный граф с К = 3
компонентами:
1
2
5
6
7
3
4
8
В+Г-Р=К+1
Выделить грани самостоятельно
9

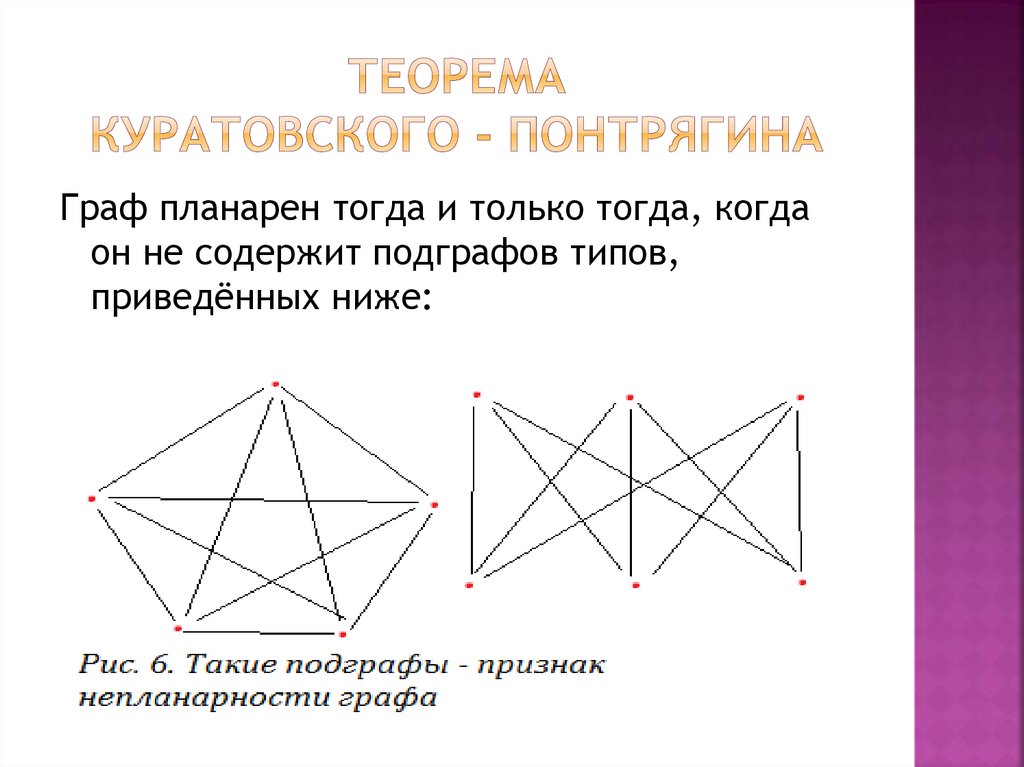
16. Теорема куратовского - понтрягина

Граф планарен тогда и только тогда, когда
он не содержит подграфов типов,
приведённых ниже:

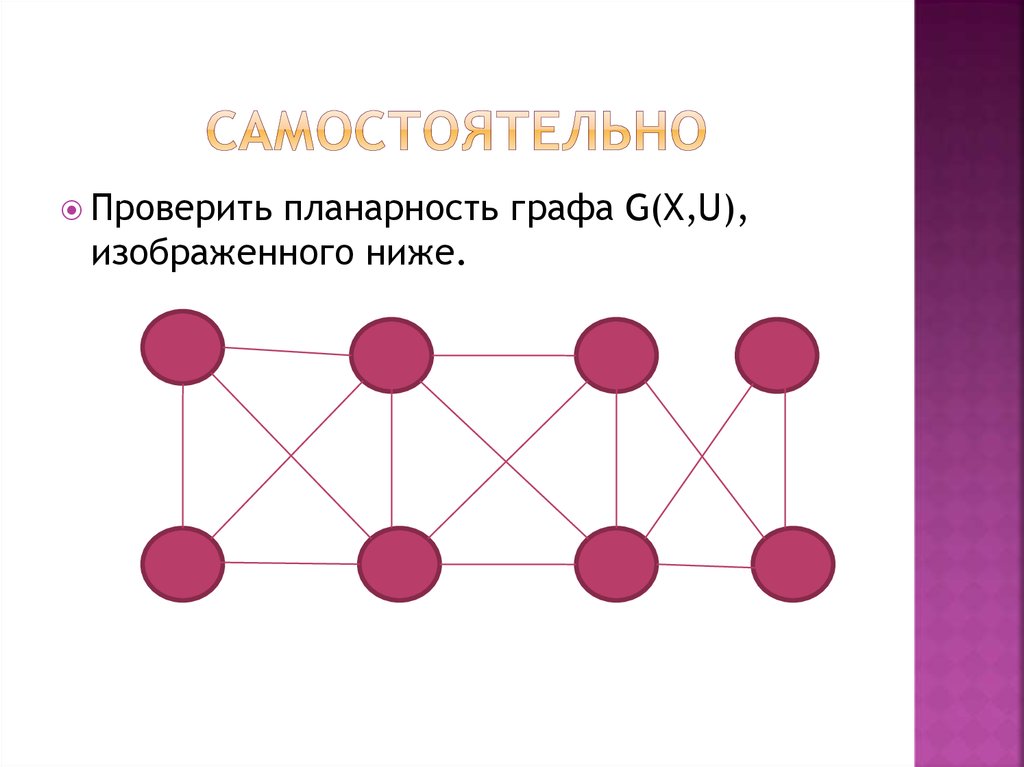
17. самостоятельно

Проверить
планарность графа G(X,U),
изображенного ниже.

18. Двойственные графы

Правила построения двойственного графа:
1. Каждая грань исходного графа заменяется
вершиной двойственного.
Если граф неориентированный, то каждое
ребро исходного графа заменяется
пересекающим его ребром двойственного.
Если исходный граф ориентированный, то
каждая дуга исходного графа заменяется
пересекающей ее дугой двойственного графа
по «правилу правой руки».
Если исходный граф является взвешенным, то
вес каждого ребра (дуги) двойственного графа
равен весу ребра (дуги), которую оно (она)
пересекает.

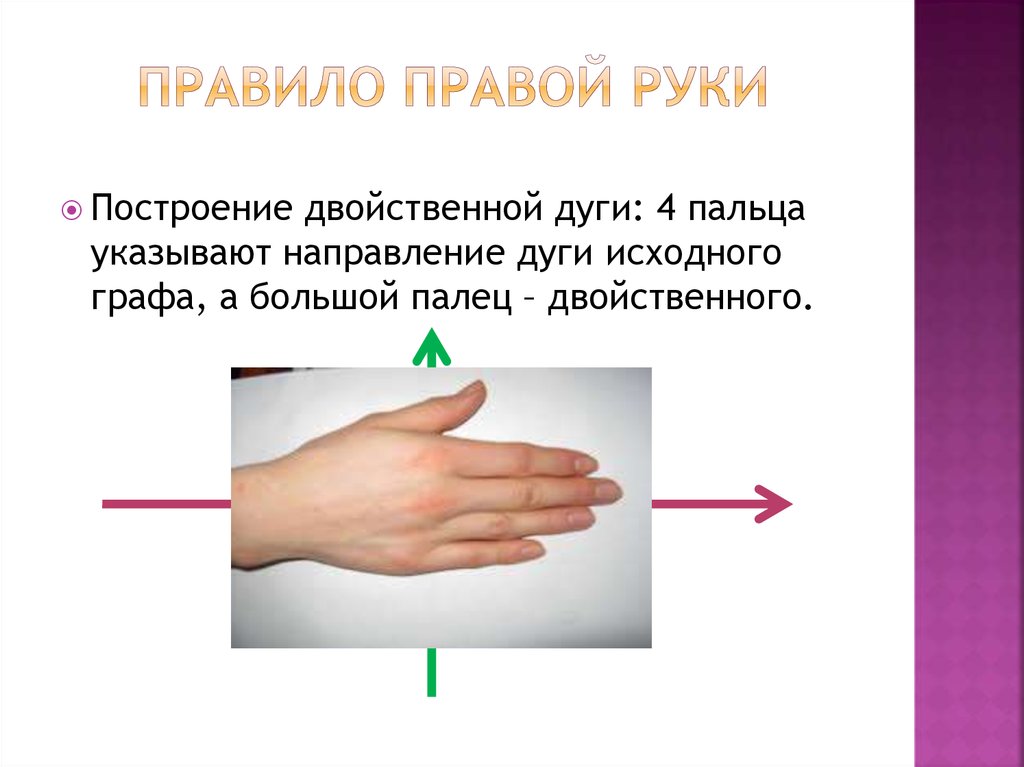
19. Правило правой руки

Построение
двойственной дуги: 4 пальца
указывают направление дуги исходного
графа, а большой палец – двойственного.

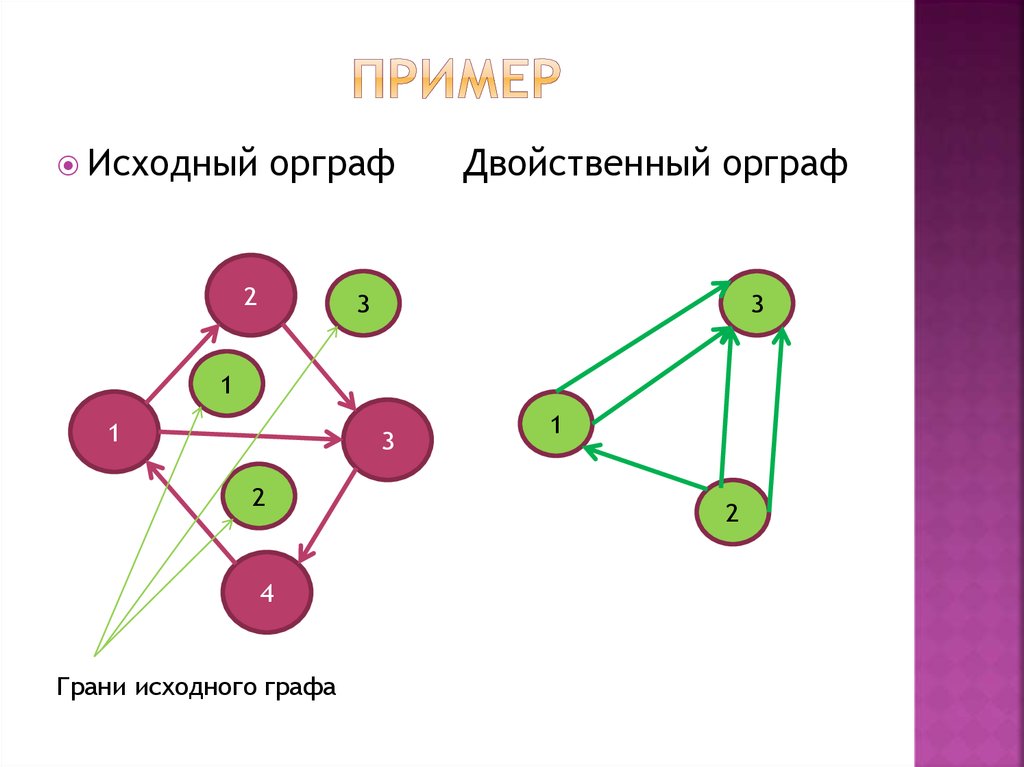
20. пример

Исходный
орграф
2
Двойственный орграф
3
3
1
1
3
2
4
Грани исходного графа
1
2

21. Свойства двойственных графов

Простому контуру исходного графа,
«закрученному» по часовой стрелке,
соответствует вершина-источник
двойственного графа.
Простому контуру исходного графа,
«закрученному» против часовой стрелки,
соответствует вершина-сток двойственного
графа.
Грани исходного графа, образованной
встречно ориентированными дугами,
соответствует вершина двойственного графа,
которой инцидентны, как заходящие, так и
исходящие дуги.

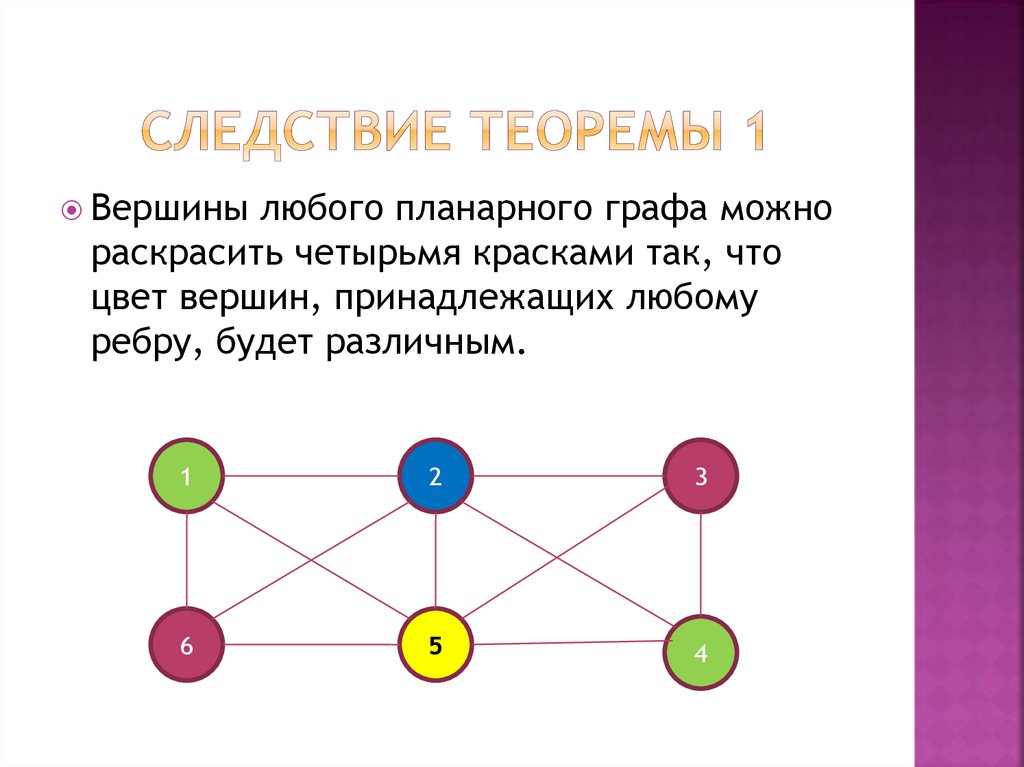
22. Следствие теоремы 1

Вершины
любого планарного графа можно
раскрасить четырьмя красками так, что
цвет вершин, принадлежащих любому
ребру, будет различным.
1
2
3
6
5
4

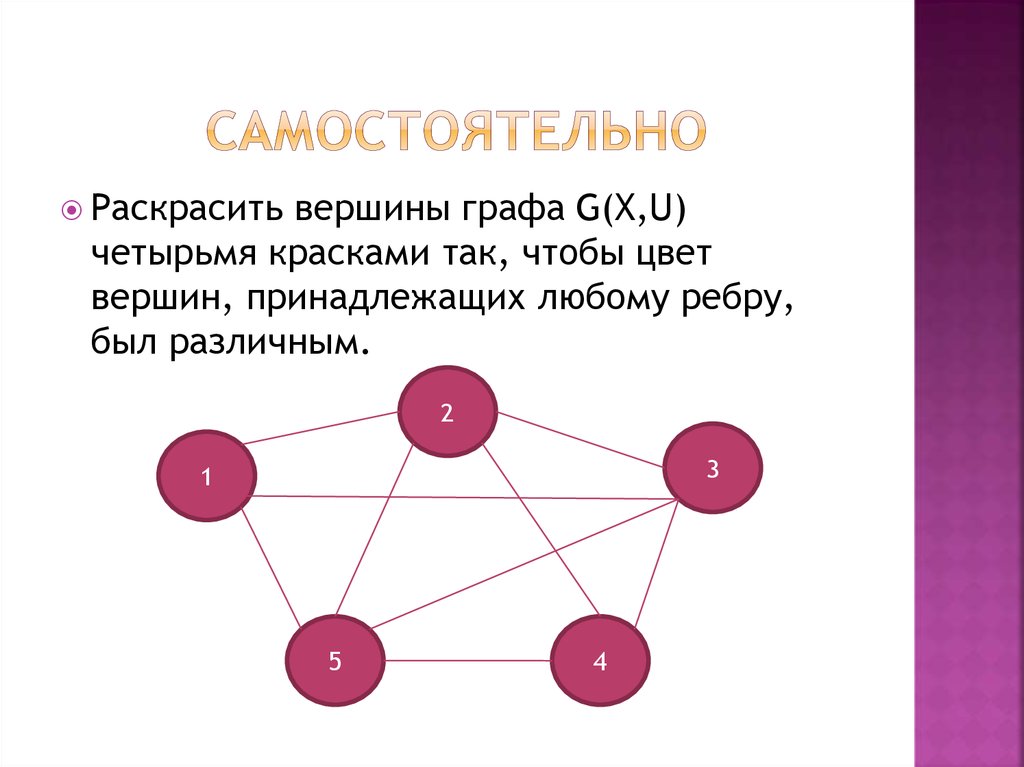
23. самостоятельно

Раскрасить
вершины графа G(X,U)
четырьмя красками так, чтобы цвет
вершин, принадлежащих любому ребру,
был различным.
2
3
1
5
4

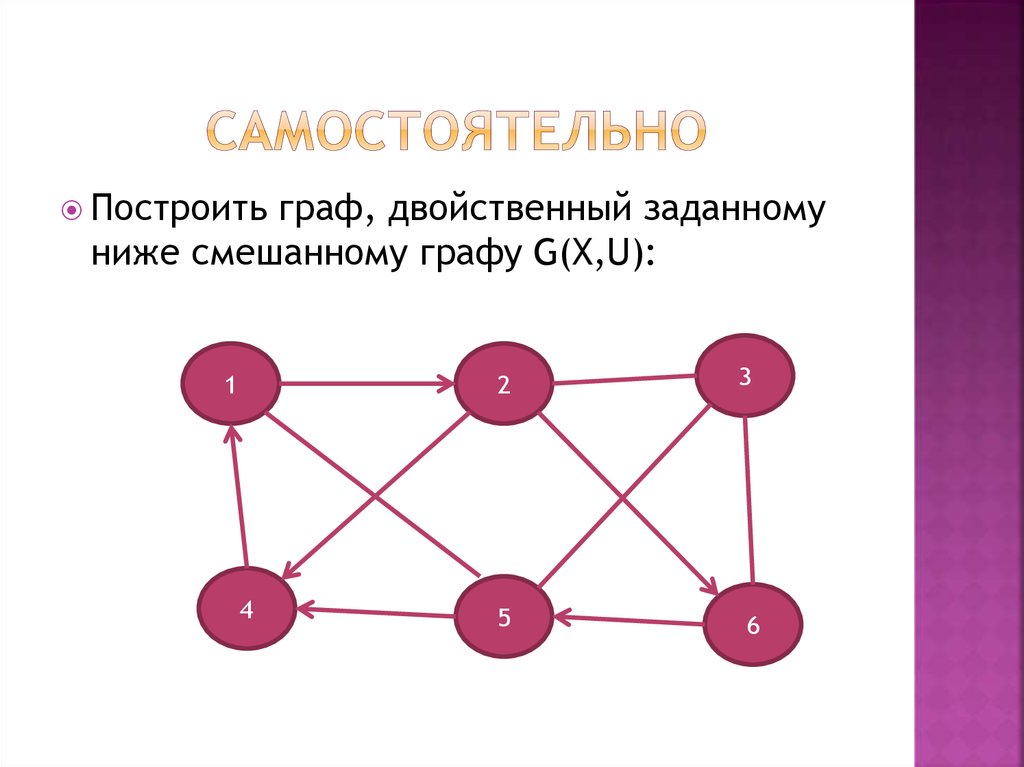
24. самостоятельно

Построить
граф, двойственный заданному
ниже смешанному графу G(X,U):
1
2
4
5
3
6

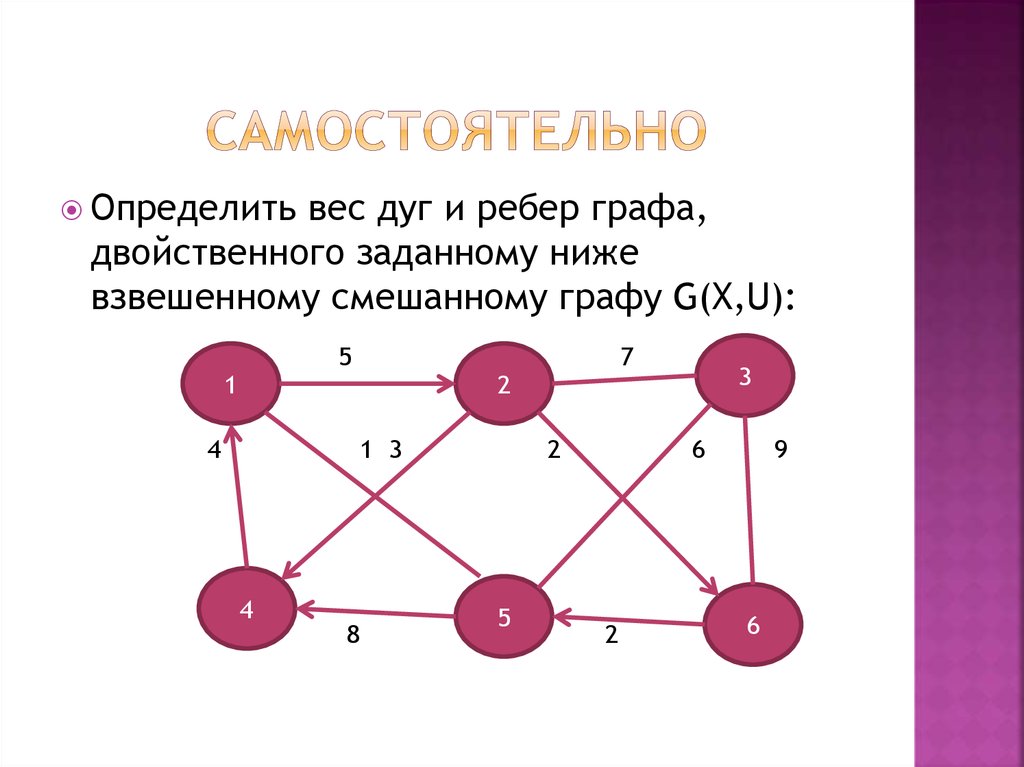
25. самостоятельно

Определить
вес дуг и ребер графа,
двойственного заданному ниже
взвешенному смешанному графу G(X,U):
5
1
4
2
1 3
4
8
7
2
5
3
6
2
9
6

26. САМОСТОЯТЕЛЬНО

Для
каких из этих тел справедлива
теорема о четырех красках?