Общая постановка задачи оптимизации

1. Общая постановка задачи оптимизации

1

2.

Целевая функция
Известные переменные или функции a1 , a2 ...
Зависящие от нас факторы или
неизвестные переменные
F
x1 , x2 ...
Целевая функция зависит от обеих
групп факторов
F F (a1 , a2 ,..., x1 , x2 ,...)
2

3. Математическая задача оптимизации

При заданных условиях a1 , a2 ...
найти такие значения x1 , x2 ... ,
которые обращают
показатель F
в минимум (максимум).
3

4. Ограниченное применение метода дифференцирования для решения задачи оптимизации

Если целевая функция, которую надо
максимизировать задана в следующем
виде и
F 2 x1 4 x2
x1 0, x2 0
Производные равны
F
F
2,
4
x1
x2
4

5. Ограниченное применение метода дифференцирования для решения задачи оптимизации

Когда переменных много, то решение
системы уравнений, полученное
дифференцированием, зачастую
оказывается не проще, а сложнее, чем
непосредственный поиск экстремума.
5

6. Этапы постановки и решения оптимизационных задач

1.
2.
3.
4.
5.
6.
Выявление всех процессов, происходящих в оптимизационной
системе для получения полной характеристики объекта
оптимизации.
Содержательная постановка задачи оптимизации для построения
математической модели и выбор метода решения. Здесь главное
отнесение задачи к определенному классу (развитие или
функционирование), выбор критерия оптимизации и целевой
функции.
Составление математической модели.
Определение математического метода решения задачи.
Разработка алгоритма решения задачи и собственно решение (как
правило, на компьютере при наличие соответствующей
программы).
Принятие оптимального решения специалистом на базе
полученного решения.
6

7. Стратегия оптимизационных исследований

8.

8

9. Составление математической модели

9

10. Целевая функция

представляет собой
математическое выражение, дающее
количественную оценку степени
выполнения требований к процессу
управления объектом
F ( x) min(max)
x - вектор заданных и зависимых
(неизвестных) переменных
10

11. Критерии оптимизации режимных задач

Издержки производства на эксплуатацию
и развитие
И И пост И пер
Критерии управления
предприятием должны
обеспечивать минимизацию
переменных составляющих
затрат
11

12. Критерии оптимизации внутристанционных режимов электростанции

Технические критерии, которые могут быть
представлены величинами расхода
энергоресурса (топлива или воды), кпд,
потерями энергии на работающих
агрегатах:
для ТЭС – минимум расхода топлива
Bст Bi ( Pi ) min,
i
либо для любой станции максимум КПД
ст i ( Pi ) max
i
Оптимизация режимов направлена на выбор оптимального
состава работающего оборудования, активных и реактивных
мощностей агрегатов.
12

13. Критерий оптимизации режимов электрической сети сетевого предприятия

Минимума
потерь активной
мощности Рt min
Минимума
потерь энергии
Эt Pt t min
t
13

14. Критерий оптимизации режимов электрической сети для нескольких сетевых предприятий, взаимодействующих при транспорте электрической эне

В интересах покупателей применяется
критерий минимума стоимости передачи
энергии всех сетевых предприятий, по
которому определяются транспортные
потоки мощностей
Ц СП Ц СПj (ЭСПj ) min
j
14

15. При оптимизации режима электроэнергетической системы

Оптимизация режима может
проводиться в различных задачах по
критериям минимума цены, минимума
издержек или максимума прибыли
Ц min
И min
П max
15

16. Ограничения на переменные

16

17. Ограничения могут быть в форме:

Равенств, отражающих зависимость между
переменными. Они основываются на известных
законах и зависимостях. Например, баланс
активной мощности:
g ( x) 0
PГ PН P 0
Неравенств, отражающих предельно
допустимые значения переменных (граничные
условия) или двухсторонние неравенства
x j min x j x j max , j 1,..., n
или однозначные
x j 0, j 1,..., n
17

18. В общем виде задача оптимизации формулируется

L F ( x) min(max)
g ( x) 0
x j min x j x j max , j 1,..., n
x j 0, j 1,..., n
18

19. Методы решения задач линейного программирования

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
19

20. Формирование математической модели по содержательной постановке задачи

Задача о рациональном
использовании ресурсов (сырья)
Задача о рациональной загрузке
оборудования
Транспортная задача
Задача о рациональной смеси
20

21. Формирование математической модели по содержательной постановке задачи

1-я группа – задачи, строго
удовлетворяющие условиям
линейного программирования:
- транспорт материалов и зап.частей;
- распределение топлива на складах;
- расстановка ремонтных бригад на
трассе.
21

22. Формирование математической модели по содержательной постановке задачи

2-я группа – задачи высокой
размерности (составление топливно –
энергетического баланса страны;
определение замыкающих затрат на
топливо и т.д.)
22

23. Формирование математической модели по содержательной постановке задачи

3-я группа – задачи, допускающие
погрешность в расчетах (развитие
энергетики, перспективное
планирование (20 лет и более),
перспективный топливно –
энергетический баланс).
23

24.

Математические предположения для задачи ЛП:
определенность (детерминированность) – все
параметры модели известны точно или могут быть
оценены;
линейность (эквивалентна пропорциональности и
аддитивности) – все функциональные соотношения
модели линейны относительно основных переменных;
пропорциональность – эффект
влияния
переменной задачи пропорционален значению этой
переменной;
аддитивность – эффект влияния нескольких
переменных задачи равен сумме эффектов от
каждой переменной;
делимость – все основные переменные задачи могут
принимать произвольные вещественные значения в
определенном диапазоне (бесконечно делимы).
24

25. Линейное программирование

Основная задача линейного
программирования

26. Стандартная форма

Первая стандартная форма задачи
линейного программирования имеет
вид

27. Стандартная форма

Вторая стандартная форма задачи
линейного программирования имеет
вид

28. Каноническая форма

Канонической
формой
задачи
линейного
программирования
называется задача вида

29. Правила приведения

Рассмотрим теперь те приёмы, которые позволяют
произвольные
формы
задач
линейного
программирования приводить к указанным выше
стандартным формам.
1. Превращение max в min и наоборот. ,
Если
целевая
функция
в
задаче
линейного
программирования задана в виде
то, умножая её на (- 1), приведем её к виду
так как смена знака приводит к смене min на max.
Аналогично можно заменить max на min.

30. Правила приведения

2. Смена знака неравенства.
Если ограничение задано в виде
то, умножая на (-1), получим:
Аналогично, неравенство вида больше либо
равно можно превратить в неравенство вида
меньше либо равно .

31. Правила приведения

3. Превращение равенства в систему неравенств.
Если ограничение задано в виде
то его можно заменить эквивалентной системой двух неравенств
или такой же системой неравенств со знаками больше либо равно.
Указанные выше приемы позволяют приводить задачи линейного
программирования к стандартной форме.

32. Правила приведения

4. Превращение неравенств в равенства.
Для приведения задачи к канонической форме, где все
ограничения имеют вид равенств, вводят дополнительные
переменные
, которые тоже считаются
неотрицательными и записывают исходную задачу в виде

33. Правила приведения

То есть в неравенстве со знаком меньше либо равно
добавляют
дополнительную
неотрицательную
переменную, а из неравенства со знаком больше
либо равно вычитают дополнительную переменную.
В целевую функцию эти дополнительные переменные
включают с коэффициентом 0, т.е. фактически они в
целевой функции отсутствуют.
Получив решение задачи в канонической форме, для
получения решения исходной задачи надо просто
выбросить из решения значения введенных
дополнительных переменных.

34.

Математически задача ЛП – задача нахождения
наибольшего (наименьшего) значения линейной функции
многих переменных при линейных ограничениях типа
равенств (неравенств), когда на переменные задачи есть
(нет) ограничений на знак.
задача максимизации ЛП задача минимизации ЛП
max z max(c1x1 cn xn )
min z min(c1x1 cn xn )
при ограничениях
при ограничениях
ai 1x1 ain xn bi , i 1, m,
ai 1x1 ain xn bi , i 1, m,
x j 0, j 1, n.
x 0, j 1, n.
j
x j , j 1, n
переменные
z c1x1 cn xn целевая функция
x j 0, j 1, n условие неотрицательности переменной
с j , aij , bi
заданные параметры
34

35.

Вектор
X ( x1 , , xn ) удовлетворяющий всем
ограничениям задачи, называется
допустимым
решением задачи ЛП.
Множеством допустимых решений задачи ЛП
называется множество векторов X ( x1 , , xn ) ,
удовлетворяющих всем ограничениям задачи.
X ( x1 , , xn ), доставляющий максимум
Вектор
(минимум) функции z при заданных ограничениях,
называется оптимальным решением задачи ЛП.
Наибольшее (наименьшее) значение целевой функции
называется значением задачи ЛП.
Решить задачу ЛП означает найти оптимальное решение и значение целевой функции.
35

36. Геометрический метод решения задачи ЛП

Пример Решим графически задачу :
max z max(5 x1 3 x2 ),
x1 x2 4,
5 x1 2 x2 10,
x1 0, x2 0.
Геометрический метод реализуется в два этапа:
• построение допустимого множества решений задачи ЛП;
• нахождение оптимального решения задачи ЛП.
36

37.

Теорема (об оптимальных экстремальных точках).
Если в задаче ЛП существует оптимальное решение, то
существует и оптимальная экстремальная (угловая) точка.
Алгоритм графического метода для задач ЛП
n 2 :
записать каждое ограничение как равенство и
нарисовать прямую;
найти для каждого ограничения допустимую область
и множество допустимых решений задачи ЛП;
найти градиент целевой функции
grad z x1, x2 z x1 , z x2 ;
нарисовать линию уровня целевой функции
z x1, x2 const;
сдвигать линию уровня в направлении градиента, до
последней точки пересечения с множеством доп.
37
решений.

38.

При решении задачи ЛП возможны случаи:
1. Задача ЛП имеет единственное решение (см.
примеры 2.4.1 и 2.4.2).
2. Задача ЛП имеет бесконечное множество решений
(пример 2.4.3) (альтернативные решения).
3. Задача ЛП не имеет оптимального решения вследствие:
a. неограниченности множества допустимых решений
b. пустоты множества.
38

39. Симплекс-метод решения задачи ЛП.

Стандартная задача максимизации
B b1, b2 , , bm
T
max z max(c1x1
ai 1x1
cn xn ),
ain xn bi , i 1, m,
x j 0, j 1, n.
Матричная и векторная форма записи
max z max CX
max z max CX ,
AX B
Ai X bi , i 1, m,
X 0
C c1, c2 , , cn
X x1, x2 , , xn
T
Am n aij
Ai ai 1, ai 2 ,
ain
X 0.
39

40.

Стандартная задача минимизации
min z min(c1x1
ai 1x1
cn xn ),
ain xn bi , i 1, m,
x j 0, j 1, n.
Матричная и векторная форма записи
min z min CX
min z min CX
AX B
Ai X bi , i 1, m
X 0
X 0.
40

41.

Каноническая задача максимизации (минимизации)
max(min)z max(min)(c1x1
ai 1x1
cn xn ),
ain xn bi , i 1, m,
x j 0, j 1, n.
Матричная и векторная форма записи
max(min)z max(min)CX
max(min)z max(min)CX
AX B
Ai X bi
X 0
X 0
41

42.

Эквивалентные преобразования.
• Нахождение
максимума
линейной
функции
эквивалентно нахождению минимума этой функции,
взятой с противоположным знаком, и наоборот:
min z max( z ),
max z min( z ).
• Если на переменную не накладывается условие
неотрицательности, то ее можно заменить разностью
двух неотрицательных переменных:
x j x j x j ,
x j 0, x j 0.
42

43.

• Если имеется n таких переменных , то их можно
заменить n+1 неотрицательной переменной:
x j x j x0 ,
x j 0, j 1, n, x0 0.
• Ограничение типа неравенства можно представить
в виде равенства, используя слабые переменные,
следующим образом:
ai 1x1
ain xn bi ai 1x1
ain xn si bi , si 0, i 1, m,
ai 1x1
ain xn bi ai 1x1
ain xn si bi , si 0, i 1, m
43

44.

• Ограничение типа равенства можно заменить
двумя неравенствами:
ai 1x1
ai 1x1
ain xn bi
ai 1x1
ain xn bi ,
ain xn bi .
• Если имеется m равенств, то их можно заменить
m+1 неравенством:
ai 1x1
ai 1x1 ain xn bi , i 1, m,
ain xn bi , i 1, m m
(ai 1x1 ain xn bi ) 0.
i 1
Знак неравенства можно заменить на противоположный,
умножив данное неравенство на (-1)!
44

45.

Базисное решение системы линейных
уравнений
max z max CX
AX B, X 0.
Пусть СЛУ AX =B совместна, т. е. выполнено условие:
rang ( A) rang ( A, B )
a11x1 a1 j x j a1n xn b1,
a11x1 a2 j x j a2 n xn b2 ,
a x a x a x b .
mj j
mn n
m
m1 1
45

46.

Базисным решением СЛУ, зависящим от
множества индексов S 1, , m
, будем называть
решение СЛУ, которое находится по указанным ниже
правилам.
• привести данную систему, используя метод Гаусса, к
диагональной форме по переменным:
x1, , xm - базисные переменные
x1
a1m 1xm 1 a1n xn b1,
xm a mm 1xm 1 a mn xn b m .
• взяв небазисные переменные, x j 0, j m 1, n
получим
x j b j , j 1, m.
46

47.

Утверждение.
Если у системы линейных уравнений существует
решение, то существует и базисное решение этой
системы ЛУ.
Утверждение.
Если задача ЛП имеет допустимое решение, то
она имеет и допустимое базисное решение.
Утверждение.
Если задача ЛП имеет оптимальное решение, то
она имеет и оптимальное базисное решение.
47

48.

Перейдем к описанию формального алгоритма
симплекс-метода
для
канонической
задачи
максимизации:
max z max (c1x1
a i 1x1
c n xn ),
a in xn b i , i 1, m,
x j 0, j 1, n.
Выполним ряд вспомогательных построений. По задаче
ЛП запишем СЛУ, рассматривая целевую функцию как
одно из ограничений (z-уравнение):
z c1x1 cn xn 0,
ai 1x1 ain xn bi , i 1, m.
48

49.

z c1x1 cn xn 0,
ai 1x1 ain xn bi , i 1, m.
Приведем данную систему к диагональной форме
по переменным: x1, , xm
z
x1
x2
cm 1xm 1
cn xn z 0 ,
a1 m 1xm 1
a1 n xn b1,
a2 m 1xm 1
a2 n xn b2 ,
xm am m 1xm 1
am n xn bm .
49

50.

Симплексная таблица представляет собой таблицу
коэффициентов диагональной формы СЛУ, построенной
для канонической задачи максимизации.
z x1
xr
xm xm 1
z z0 0
0
0
x1 b1 1
0
xr
0
xm b 0
m
br
cm 1
xs
xn
cs
cn
0 a1 m 1
a1s
a1 n
1
0 ar m 1
ar s
ar n
0
1 am m 1
am s
am n
50

51.

Классификация симплексных таблиц:
симплексная таблица называется прямо-допустимой,
если
bi 0, i 1, m ,
симплексная таблица называется двойств.-допустимой, если
c j 0, j 1, n ,
симплексная таблица называется оптимальной, если
она одновременно и прямо-допустимая, и двойственнодопустимая.
Оптимальная
СТ
соответствует
оптимальному базисному решению.
51

52. Алгоритм прямого симплекс-метода (максимизация)

0. Начать вычисления с прямо-допустимой СТ.
ИТЕРАЦИЯ
1. Проверка оптимальности или нахождение
ведущего столбца СТ.
c j 0, j 1, n , то текущее базисное
• Если
решение является оптимальным.
• В противном случае в базис вводим переменную
номер которой находится по правилу:
xs ,
cs min c j
c j 0
Столбец s называется ведущим столбцом СТ.
52

53.

2. Проверка условия неограниченности задачи ЛП или
нахождение ведущей строки СТ.
• Если в ведущем столбце все коэффициенты
ais 0, i 1, m,
то решение задачи неограниченно.
• В противном случае следует выводить из базиса
переменную, для которой:
br
bi
min
ars ais 0 ais
Строка под номером r называется ведущей строкой СТ,
ars 0 ведущим элементом СТ,
3. Преобразование СТ.
53

54.

ведущий столбец
xr
xm xm 1
z z0 0
0
0
x1 b1 1
0
xr
0
xm b 0
m
br
cm 1
xs
xn
cs
cn
0 a1 m 1
a1s
a1 n
1
0 ar m 1
ar s
ar n
0
1 am m 1
am s
am n
алгоритм
ведущая строка
z x1
54

55.

Транспортная задача (ТЗ)
Содержательная постановка:
A1, A2, , Am
пункты производства
a1, a2 , , am
производительность
B1, B2, , Bn
пункты потребления
b1, b2 , , bn
ci j 0
спрос
удельные транспортные затраты
Транспортная задача заключается
в определении плана перевозок, при котором удовлетворен
спрос каждого потребителя, вывезен весь объем
продукции из каждого пункта производства и при этом
суммарные транспортные затраты минимальны.

56.

Способы задания ТЗ
• аналитический
C cij , cij 0,
• табличный
a a1, a2, , am , ai 0, i 1, m
b b1, b2, , bn , b j 0, j 1, n
,
• сетевой
b1
b2
bn
a1
c11
c12
c1n
a2
c21
c22
c2 n
am
c m1 c m 2
cmn

57.

Математическая модель транспортной задачи
m
min z min(c11x11 c12 x12
xi 1 xi 2
x1 j x2 j
n
min z min cij xij
cmn xmn )
i 1 j 1
n
x
xin ai , i 1, m,
ij
ai , i 1, m,
j 1
m
xmj bj , j 1, n,
x
ij
b j , j 1, n,
i 1
xij 0, xij целые.
xij 0, xij целые.
Теорема 3.4.1. (О разрешимости ТЗ)
Для существования оптимального решения ТЗ,
необходимо и достаточно, чтобы выполнялось условие
m
n
баланса:
ai b j .
i 1
j 1

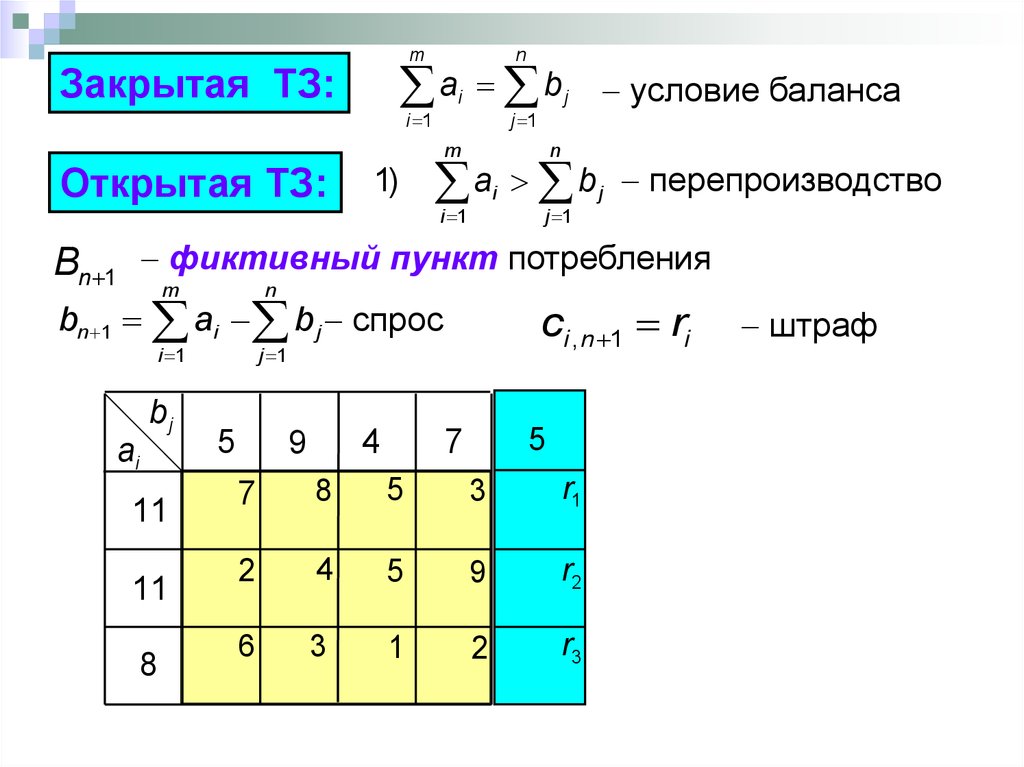
58.

m
n
a b
Закрытая ТЗ:
i
i 1
Открытая ТЗ:
j 1
m
1)
j
условие баланса
n
a b
i
i 1
j
перепроизводство
j 1
Bn 1 фиктивный пункт потребления
m
n
bn 1 ai b j спрос
i 1
bj
ai
11
11
8
ci , n 1 ri
j 1
5
4
9
5
7
7
8
5
3
r1
2
4
5
9
r2
6
3
1
2
r3
штраф

59.

m
Открытая ТЗ:
2)
n
a b
i 1
i
j 1
j
- дефицит
фиктивный пункт производства
Am 1
n
m
j 1
i 1
am 1 b j ai производительность
bj
ai
11
6
8
5
5
9
9
7
7
8
5
3
2
4
5
9
6
3
1
2
r1
r2
r3
r4
cm 1, j r j

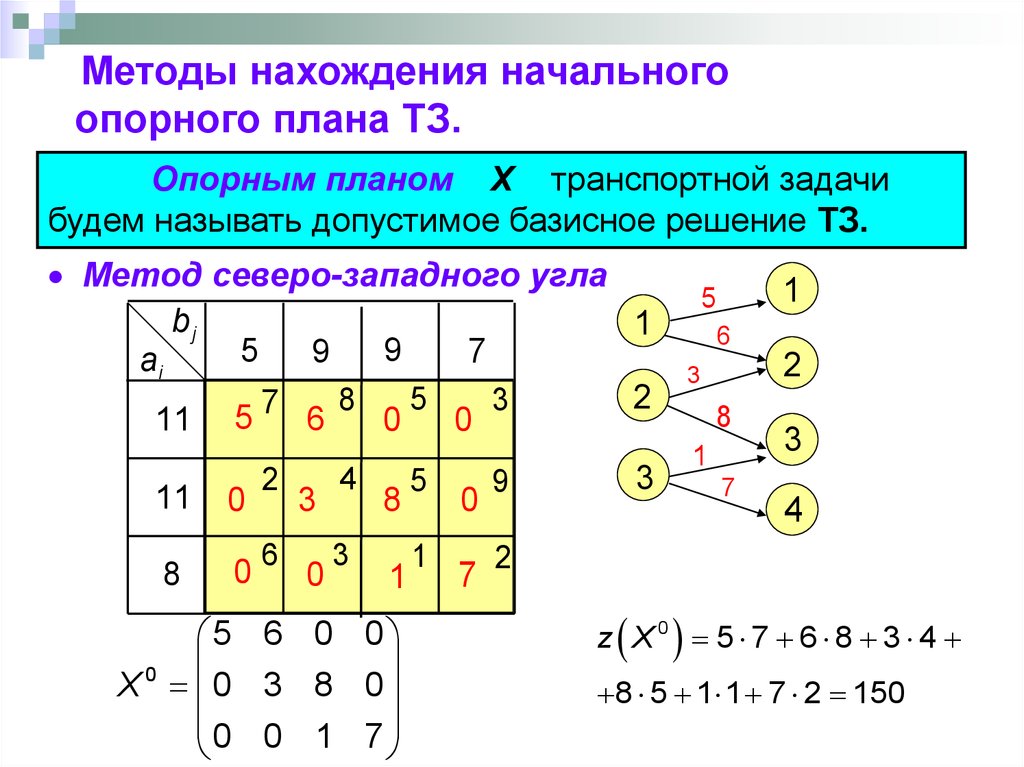
60.

Методы нахождения начального
опорного плана ТЗ.
Опорным планом X транспортной задачи
будем называть допустимое базисное решение ТЗ.
Метод северо-западного угла
bj
1
9
5
7
9
ai
2
5
8
3
7
6
11 5
0
0
11
0
8
0
2
6
3
0
4
3
8
1
5 6 0 0
X0 0 3 8 0
0 0 1 7
5
1
0
7
9
3
1
5
6
2
3
8
1
7
3
4
2
z X0 5 7 6 8 3 4
8 5 1 1 7 2 150

61.

Метод минимального элемента
bj
ai
11
11
8
1
5
0
5
0
9
9
7
2
6
3
6
0
8
4
3
1
0
8
1
7
5
5
1
7
0
0
3
9
2
2
2
3
3
4
0 3 1 7
X0 5 6 0 0
0 0 8 0
z X 0 3 8 1 5 3 7 2 5 6 4 8 1 92

62.

Метод Фогеля
bj
ai
11
11
8
штрафы
столбцов
5
0
7
8
3
6
5
6
4
1
4
2
0
9
9
0
0
3
8
штрафы строк
7
5
5
1
7
0
0
3
2
2
2
3
9
2
1
1
1
2
1
1
1
4
1
1
4
1
4
0
6
4
0
0 3 1 7
X0 5 6 0 0
0 0 8 0
z X 0 92

63.

Проверка плана ТЗ на опорность
(метод вычеркиваний):
• вычеркнуть все строки в матрице Х, содержащие не
более одного положительного элемента;
• в получившейся матрице вычеркнуть все столбцы,
содержащие не более одного положительного элемента;
• далее процесс вычеркивания строк и столбцов применяется к оставшейся подматрице.
Процесс заканчивается одним из двух исходов:
1. Все строки (столбцы) вычеркнуты. Тогда Х опорный.
2. Получена подматрица, в каждой строке (столбце)
которой не менее 2 положительных элементов. Х не
опорный. Из оставшихся элементов можно построить
цикл.