Исследование возможности задач классификации методом логистической регрессии

1. Исследование возможности задач классификации методом логистической регрессии

ИССЛЕДОВАНИЕ
ВОЗМОЖНОСТИ ЗАДАЧ
КЛАССИФИКАЦИИ МЕТОДОМ
ЛОГИСТИЧЕСКОЙ РЕГРЕССИИ
Выполнил студент группы ПМБС11
Колотова Валерия
Кафедра «Приборостроение»

2. Постановка задачи

В данной выпускной
квалификационной работе
рассматривается исследование
возможности решения задач
классификации методом
логистической регрессии.
В ходе исследования была
использована случайная выборка,
содержащая экспериментальную и
контрольную группы, в числе 174
значений, 145- нормы, 29- патологии.

3. Актуальность статистики в медицине

Статистическая обработка медицинских исследований
базируется на принципе того, что верное для
случайной выборки верно и для генеральной
совокупности, из которой эта выборка получена.
Однако выбрать или набрать истинно случайную
выборку из генеральной совокупности практически
очень сложно. Поэтому следует стремиться к тому,
чтобы выборка была репрезентативной по отношению
к изучаемой системе , т.е. Достаточно адекватно
отражающей все возможные аспекты изучаемого
состояния или заболевания , чему способствует чёткое
формулирование цели и строгое соблюдение
критериев включения и исключения как в
исследовании, так и в статистическом анализе.

4. Виды статистических данных в медицине

Статистические данные могут быть
представлены как
количественными(числовыми непрерывными
или дискретными), так и качественными
(категориальными порядковыми или
номинальными) переменными. Необходимо
чётко указывать тип (вид) переменной при
заполнении базы данных и точно
придерживаться выбранного типа данных,
так как от этого может зависеть
дальнейшая обработка переменных во
многих используемых в настоящее время
статистических программах.

5.

Количественные (числовые) данные предполагают,
что переменнаяпринимает некоторое числовое
значение. Из них выделяют дискретные данные,
которые могут принимать строго определённые
значения, в то время как непрерывные могут быть
представлены любыми значениями.
Категориальность является основой смыслового
понимания качественных переменных.
Категориальные данные применяются для описания
состояния объекта путем присвоения ему номера,
соответствующего категории, к которой этот
объект принадлежит. Важным условием для
применения категориальных данных является
принадлежность одного объекта исследования только
к одной возможной категории для одного критерия.

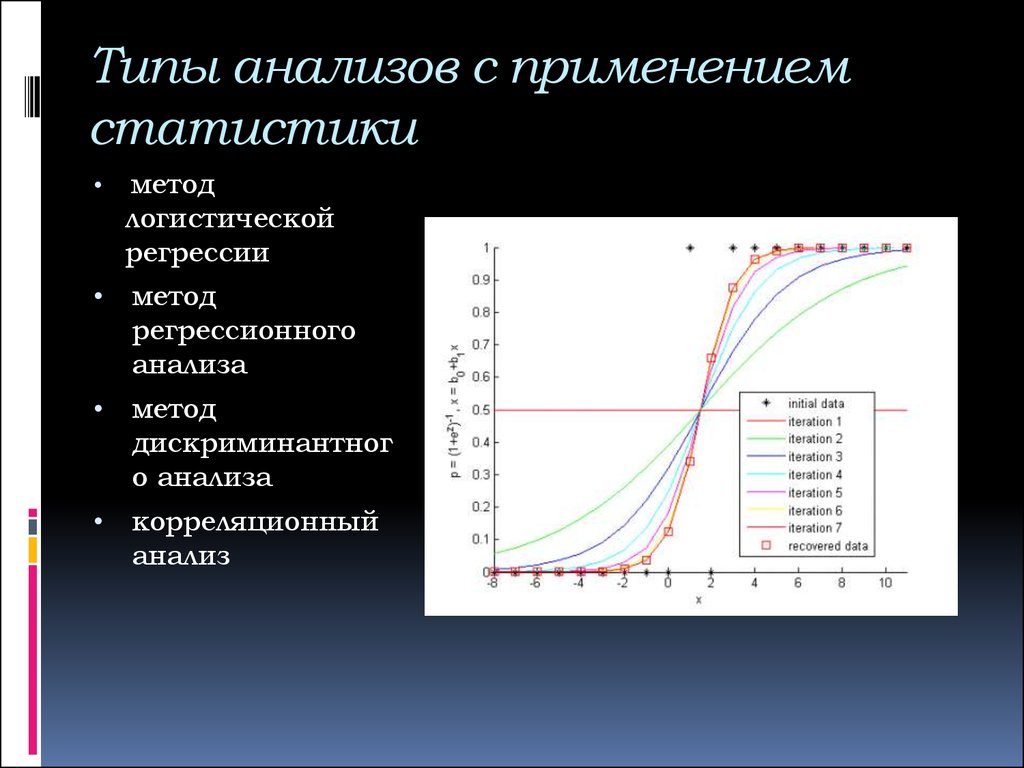
6. Типы анализов с применением статистики

метод
логистической
регрессии
метод
регрессионного
анализа
метод
дискриминантног
о анализа
корреляционный
анализ

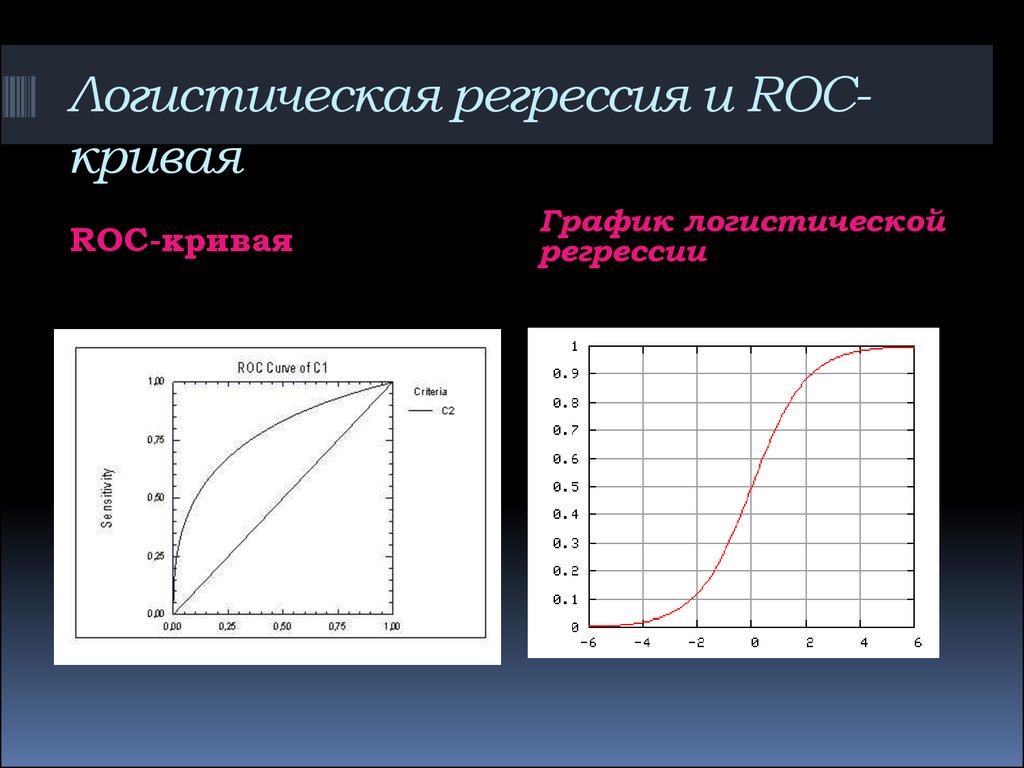
7. Логистическая регрессия и ROC-кривая

Логистическая регрессия и ROCкривая
ROC-кривая
График логистической
регрессии

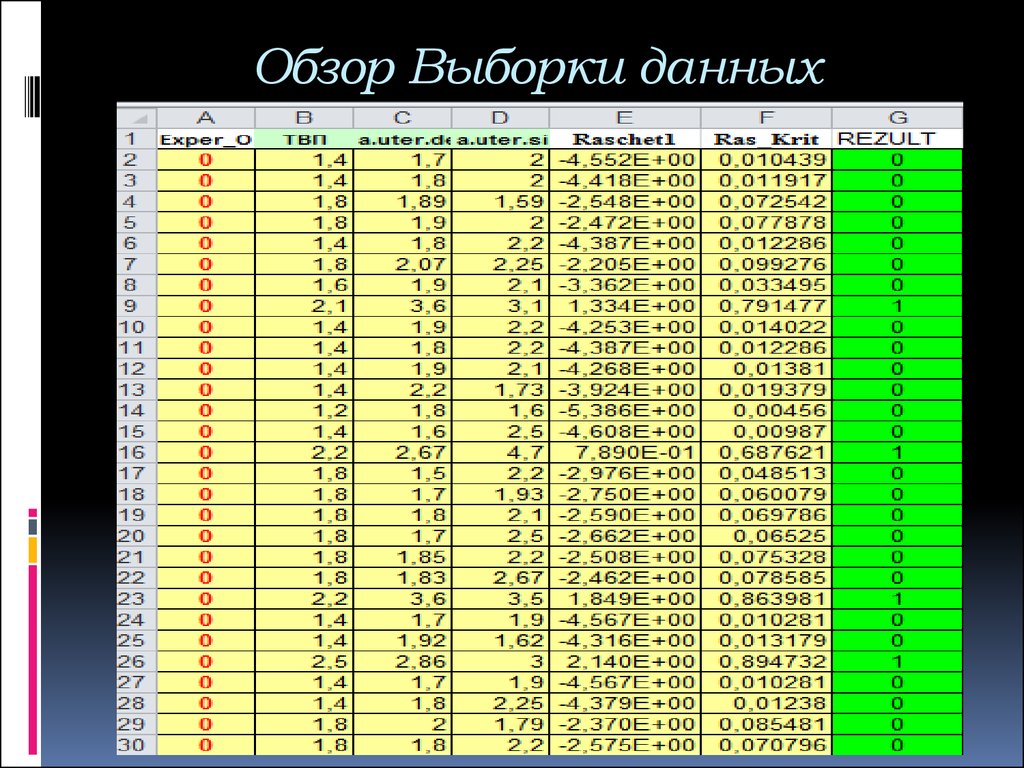
8. Обзор Выборки данных

9. Чувствительность, специфичность ,общая точность

Чувствительность–это и есть доля истинно положительных случаев:
способность выявлять заболевание - так как она отражает соотношение
правильных заключений к 1 общему числу окончательных диагнозов в
этой 1 группе больных, ее все чаще представляют под 1 названием
"информативность" в работах, когда анализируют фактический
материал в процентах.
Специфичность– доля истинно отрицательных случаев, которые были
правильно идентифицированы моделью: чем чаще мы ставим
неправильный диагноз, т.е. занимаемся гипердиагностикой, тем ниже
будет "специфичность" выполняемого исследования, так как
"специфичность" - это способность метода отвергать заболевание,
констатировать его отсутствие там, где его действительно нет.
Общая точность - соотношение числа достоверно положительных и
достоверно отрицательных заключений к общему числу окончательных
диагнозов.

10. Описательная статистика

Одной из основных составляющих любого анализа данных является
описательная статистика (дескриптивная статистика). Её главной задачей
является предоставление сжатой и концентрированной характеристики
изучаемого явления в числовом и графическом виде.
Мода (Мо)— это наиболее частое значение в выборке, или среднее
значение класса с наибольшей частотой.
Медиана (Me, Md) соответствует центральному значению в
последовательном ряду всех полученных значений или среднему
значению наиболее часто встречающихся значений выборки.
Среднее арифметическое (М)— это показатель центральной тенденции,
полученный делением суммы всех значений данных на число этих данных.
Среднее арифметическое используется для представления
количественных переменных с нормальным распределением.

11. Процедура обработки данных

С целью объективизации оценки полученных
в работе данных были произведены расчеты
точности, чувствительности и
специфичности предлагаемого метода
диагностики . При анализе качества
диагностики учитывали несколько
альтернативных решений, в основе которых
было совпадение или несовпадение
диагноза «норма» или «патология» .

12.

истинно положительное решение –
совпадение диагноза по всем учтенным
методикам;
ложноотрицательное решение –
отсутствие признаков ФПН при наличии
критериев патологии;
ложноположительное решение наличие патологии по результатам
исследования;
истинно отрицательное решение –
отсутствие патологии по всем учтенным
методикам.

13. Программная реализация в пакете MATLAB

functionLogit_Regressya
%функция построения графиков логистической регрессии
clc;
clearall;
closeall;
%Const b0 ТВПuter.decstruter.sinistr
%-13.4803 4.531 1.33889 0.154526
%0-2:145 1-146:174
%Чтение числовых данных и заголовков столбцов из MS Excel
Dat=xlsread('D:\Dat_Kolotova.xls','Лист1');
%выделение массивов входных данных
Exper_O=Dat(:,1);%
TVP=Dat(:,2);%
uter_dex=Dat(:,3);%
uter_sin=Dat(:,4);%
%
TolFun=0.005;%заданная точность итерации
%вектор имен полей данных

14. Основные функции и подпрограммы

Подбор значений вектора коэффициента осуществляется с
использованием итерационной процедуры по заданному
значению точности: TolFun=0.005;% , заданная точность
итерации
j=1;
while 1==1
Умножение матрицы данных на вектор коэффициента:
Z=X*b;
Функция логистической регрессии:
p=1./(1+exp(-Z));
w=p.*(1-p);
u=Z+(y-p)./w;
Итерационная процедура:
b_old=b;
D(:,j)=1./(1+exp(-X*b));
B(:,j)=b;
j=j+1;

15. Результаты обработки выборки данных

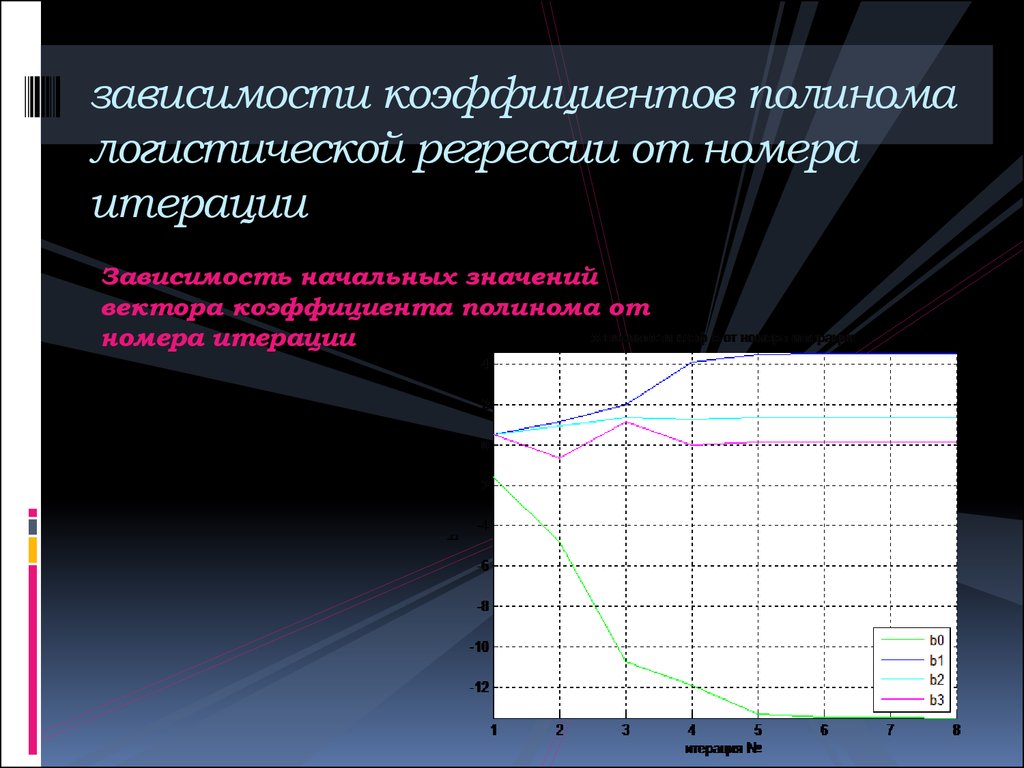
Изображение исходных данных

16. зависимости коэффициентов полинома логистической регрессии от номера итерации

Зависимость начальных значений
вектора коэффициента полинома от
номера итерации

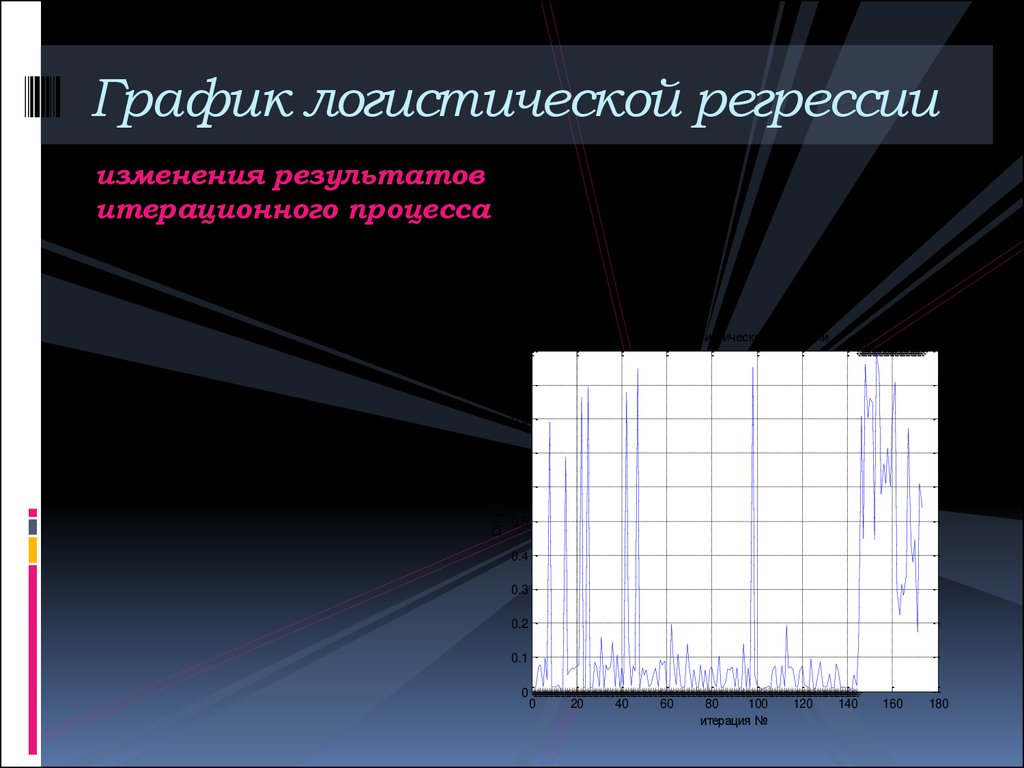
17. График логистической регрессии

изменения результатов
итерационного процесса
графики логистической регрессии
1
0.9
0.8
0.7
D(i,j)
0.6
0.5
0.4
0.3
0.2
0.1
0
0
20
40
60
80
100
итерация №
120
140
160
180

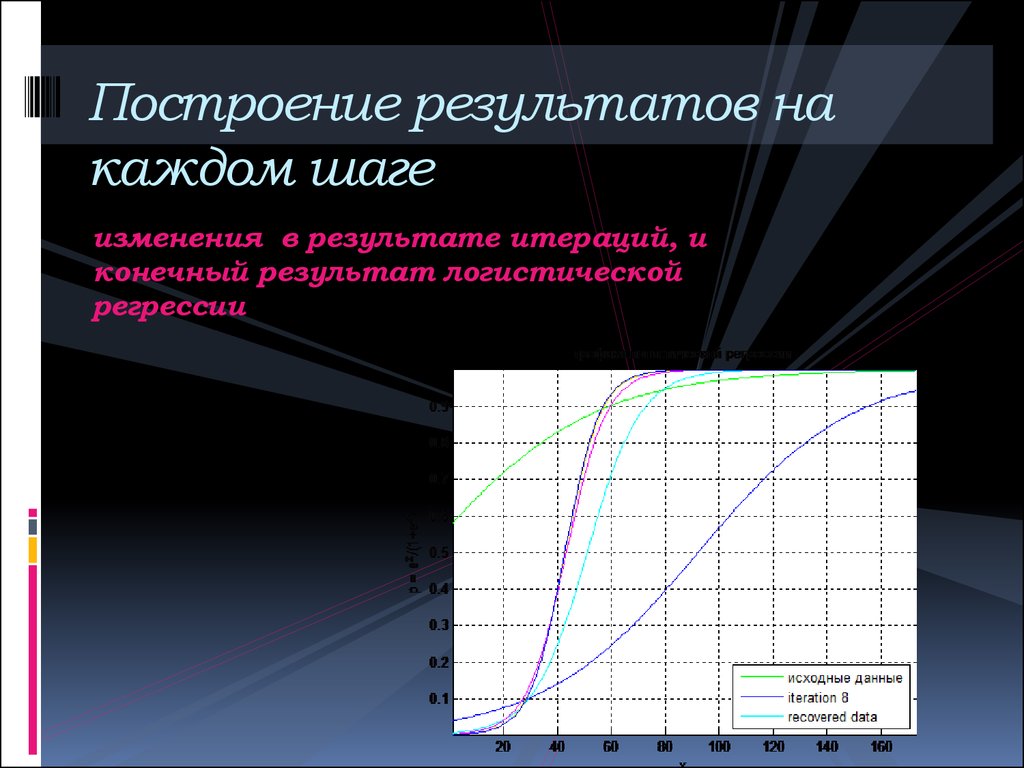
18. Построение результатов на каждом шаге

изменения в результате итераций, и
конечный результат логистической
регрессии

19. Вывод по исследуемой теме

Поставленная задача была выполнена полностью. В данной
работе были проведены разработка программы в среде п.п.п.
MATLAB , статистическая обработка медицинских данных, из
которых была получена случайная выборка генеральной
совокупности. Был проведен анализ всех методов обработки:
метод логистической регрессии, метод дискриминантного
анализа, корреляционный анализ.
Проведенный регрессионный анализ позволил определить
зависимость экспериментальной и контрольной групп.
На рисунках 1,2,3,4 представлены графики итерационной
процедуры, зависимости коэффициентов и функции
логистической регрессии. Обработка, программное
отображение результатов, графическое отображение
результатов проводилось с помощью пакета MATLAB.

20. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Логистическая регрессия в медицине и биологии
1998 - 2015, журнал "Медицинские технологии.
Оценка и выбор", 2014, №1, с. 17-28.
Леонов В.П.
http://www.basegroup.ru/library/analysis/regressio
n/logistic - ROC-анализ - математический аппарат.
http://www.basegroup.ru/library/practice/logis_med
ic_scoring/ -Применение логистической
регрессии в медицине и скоринге.
http://www.statistica.ru/- Решение задач с
применением статистики
Лекции по алгоритмам восстановления
регрессии - К. В. Воронцов 21 декабря 2007 г.

21. Спасибо за внимание!!!