Похожие презентации:
Электромагнитное взаимодействие
1. ОБЩАЯ ФИЗИКА
ЭЛЕКТРОМАГНИТНОЕВЗАИМОДЕЙСТВИЕ
Курс лекций
2.
Вид контроляКоллоквиум 1
Коллоквиум 2
ИДЗ 1-3
ЭКЗАМЕН
Неделя
8
16
4, 8, 12
Вид занятий
Объем в часах
Аудиторные
Самостоят.
Лекции
Практические зан.
Лабораторные раб.
36
36
18
18
18
9
Итого
90
45
Рекомендуемая литература
ОСНОВНАЯ
ДОПОЛНИТЕЛЬНАЯ
1. Тюрин Ю. И., Чернов И. П, Крючков Ю. Ю.
Электричество и магнетизм. Электродинамика.
М. Высшая школа. 2007
1. Сивухин Д.В. Общий курс физики. 3-4тт. М.
Наука. 1979-89
2. Савельев И.В. Курс общей физики. 2т. М.
Наука. 1982, Санкт-Петербург, 1996
3.
ЭЛЕКТРОМАГНИТНОЕВЗАИМОДЕЙСТВИЕ
Введение
В макроскопическом мире
основную роль играют гравитационное
и электромагнитное взаимодействия.
Остальные взаимодействия (сильное и
слабое) пространственно свернуты или
как говорят – компактифицированы и не
проявляются в макромире.
Из всех видов, гравитационное взаимодействие является наиболее слабым,
но гравитация является доминирующей силой в космических масштабах, где ее
слабость компенсируется одним только количеством атомов, дружно проявляющим
этим силу.
Гравитация связывает звезды в галактики и сохраняет Солнце в целости, а
её семейство планет удерживает на их орбитах. Она не отпускает Луну от Земли и
удерживает на своих местах океаны и атмосферу.
Отметим, что гравитационное взаимодействие проявляется только в
притяжении и зависит от одного вида «гравитационного заряда» (массы) и
ограничений на величину массы не существует.
Это приводит к тому, что за счет гравитационного взаимодействия могут
образовываться объекты космических масштабов, например галактики.
4.
ЭЛЕКТРОМАГНИТНОЕВЗАИМОДЕЙСТВИЕ
Введение
Но когда дело доходит до объектов, размер которых достигает нескольких
километров (на Земле), гравитационная сила уступает место электромагнитной силе.
Гравитация пытается, но не может остановить рост дерева или образование
горы. Электромагнитное взаимодействие является пространственно локальным,
компактифицированным по сравнению с гравитационным.
Законы этих взаимодействий одинаковы по форме и имеют одинаковый
радиус действия (бесконечный). Сравним силы электрического и гравитационного
взаимодействий не для произвольных тел, а для фундаментальной частицы,
например протона.
mp
q 2p
Fк
1
2
Fг
4 0G m p
Fг
Fг
mp
r
Fк
1
1,6 10 19
4 3,14 8,85 10 12 6,67 10 11 1,67 10 27
qp
2
2
1,24 1036
qp
Fк
5.
ЭЛЕКТРОМАГНИТНОЕВЗАИМОДЕЙСТВИЕ
Введение
Отсюда следует, что электромагнитное взаимодействие превосходит
гравитационное примерно в 1036 раз (огромное число!) при одинаковом бесконечно
большом радиусе действия.
Как же Природа выходит
из этого положения,
делая столь
высокоинтенсивное взаимодействие, пространственно локальным?
Такая компактификация электромагнитного взаимодействия связана с тем,
что существует два вида электрических зарядов – положительный и отрицательный.
Из-за высокой интенсивности электромагнитного взаимодействия закон
сохранения заряда (величина положительного заряда с высокой точностью равна
величине
отрицательного заряда, вещество в обычных условиях –
электронейтрально) накладывает ограничения на величину заряда.
Невозможно разделять заряды до бесконечно большой величины –
возникает пробой диэлектрика из любого вещества, и заряды нейтрализуются
(например, молнии во время грозы).
Даже такой диэлектрик, как вакуум (не проводит постоянный
электрический ток) пробивается высокоинтенсивным электромагнитным полем
(гамма-квантом) – образуется пара электрон-позитрон (эффект рождения пары).
6.
ЭЛЕКТРОМАГНИТНОЕВЗАИМОДЕЙСТВИЕ
Введение
Следовательно, взаимодействие двух видов электрических зарядов приводит
к тому, что между нейтральными молекулами вещества действуют силы Ван-дерВаальса, которые обусловлены электромагнитным взаимодействием, но являются
лишь слабым следом этого взаимодействия.
Подобная ситуация возникает для сильного взаимодействия (ядерные силы),
которое является слабым следом кварк-глюонного взаимодействия.
С другой стороны, в отличие от гравитационного взаимодействия, которое
зависит только от расстояния (координат) между взаимодействующими телами,
электромагнитное взаимодействие зависит от координат, скорости и ускорения
зарядов.
Если относительно инерциальной системы отсчета заряды покоятся, то
проявляется зависимость только от координат, поэтому данный раздел называется –
электростатикой.
Если относительно инерциальной системы отсчета заряды движутся с
постоянной скоростью, то возникает постоянный электрический ток и магнитное
поле постоянного тока.
При
движении
зарядов
с
ускорением
возникает
переменное
электромагнитное поле, которое отрывается от зарядов и существует
самостоятельно в виде электромагнитных волн (фотонов), движение которых
рассматривается в разделе – электродинамика.
7.
ЭЛЕКТРОСТАТИКАЭто наименьший по абсолютной величине заряд, которым
Элементарный
обладают
некоторые
элементарные
частицы,
электрический заряд
наблюдаемые в свободном состоянии.
Величина этого заряда в СИ равна е = 1,6 10 19 Кл.
Заряд обладает особым свойством – дискретностью. Поэтому заряды всех
тел q кратны величине элементарного заряда q ne,
где n – целое число.
Закон сохранения заряда.
q1
+
q2
r2 – r1
F21
+
r1
r2
0
Y
q
i
const.
i
Два точечных электрических заряда взаимодействуют
между собой с силой пропорциональной произведению
этих зарядов и обратно пропорционально квадрату
расстояния между ними.
Закон Кулона.
Z
В электрически изолированной системе
полный заряд системы сохраняется
F21
1
q1q2
4 0 r2 r1
3
r2 r1 ,
где ε0 = 8,85·10-12 Ф/м электрическая
постоянная.
X
Одноименные заряды отталкиваются,
разноименные – притягиваются.
8.
ЭЛЕКТРОСТАТИКАЗакон Кулона.
Обычно, в частном случае, один из зарядов помещают в начало
координат, например q1, тогда r1 = 0, а r2 = r и закон примет вид
F21
Принцип суперпозиции
электрических полей
1
q1q2
r.
3
4 0 r
Если зарядов более двух, то закон Кулона следует
дополнить установленным экспериментально фактом:
сила, действующая на заряд q, есть векторная сумма
кулоновских сил, действующих со стороны всех прочих
зарядов qk.
qqk rk
F
Fk .
2
rk
k 4 0 rk
k
1
Здесь rk – расстояние между зарядом q и qk.
9.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Напряженность
электрического поля
q
+
-
r
E
r
q0
+
Силовой характеристикой поля является напряженность
электрического поля Е – это физическая величина
численно равная силе, действующей на точечный
единичный положительный заряд помещенной в данную
точку поля.
F
E
,
q
0
E
где q0 – пробный заряд.
Напряженность электрического поля точечного заряда.
q0
+
1 q
1 q
E
r, E
.
3
2
4 0 r
4 0 r
10.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Принцип
суперпозиции
электрических полей
Поле системы точечных зарядов определяется как
векторная сумма напряженностей электрических полей
каждого из зарядов.
F
E
q
q1
+
E2
r2
r1
E
E1
qk
4
2
r
0 k
k
q2
q1
+
+
rk
rk
E2
r1
E1
Ek
k
q2
r2
E
Формула
для
E
позволяет
рассчитать
напряженность электрического поля любой системы
неподвижных зарядов.
11.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Для наглядного изображения электрических полей
используют понятие силовых линий.
Электрические
Это
математические
линии,
проведенные
в
силовые линии
пространстве таким образом, чтобы вектор напряженности
электрического поля был направлен по касательной в каждой
точке этой линии.
Е1
По густоте силовых линий можно
Е2
○
○
1
судить
о
величине
напряженности
2
электрического поля.
Силовая линия
3○
Е3
Положительным
направлением
силовой
линии
условно
считается
направление вектора Е.
Поэтому
для
неподвижных
или
неускоренных зарядов силовые линии начинаются
на положительных зарядах, а заканчиваются на
отрицательных (или уходят на бесконечность).
12.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Понятие о силовых линиях поля, к сожалению, не удовлетворяет основному
принципу электродинамики – принципу суперпозиции.
Если мы знаем, как выглядят силовые линии одной и другой совокупности
зарядов, то мы тем не менее не получим из этих картин характера силовых линий,
если эти совокупности зарядов действуют совместно.
Хотя силовые линии и дают наглядную картину поля, но такой способ
описания не лишен недостатков.
Поле, силовые линии которого параллельные прямые и имеют одинаковую
густоту, называется однородным, в противном случае – неоднородным.
13.
ЭЛЕКТРОСТАТИКАdS
Электрическое поле
Поток вектора напряженности
электрического поля
Элементарный поток
n
d EdS EdS cos .
S
Поток через поверхность S
E
n
E
dS
EdS .
S
14.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Поток через замкнутую
поверхность S
EdS
S
E
E
S
Величина Ф равна числу силовых линий, пересекающих поверхность S.
15.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Покажем на примере точечного заряда, что число силовых линий
поверхности S.
Теорема Гаусса (поток Ф) остается постоянным для любой замкнутой
n
q
+
E
dS
Ed S
S
r
EdS
S
q
4 0
q
4 0
q
4 0
dS
2
r
d
4
4
q
0
.
Следует заметить, что полученный результат не зависит от r и поэтому
справедлив для всех значений r. Таким образом, полное число силовых линий,
выходящих из точечного заряда q, равно q/ε0, и эти линии непрерывны на всем пути
до бесконечности.
16.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Теорема Гаусса
Число силовых линий равно Ф = q/ε0, даже если замкнутая
поверхность не является сферой. Если поверхности
dS и dS
пересекает одно и то же число линий, то ( EdS ) ( EdS ),
и, следовательно,
E, d S E, d S ,
S
По сфере
где S замкнутая поверхность любой формы, охватывающая заряд q.
Теперь допустим, что внутри замкнутой поверхности находятся n точечных
зарядов
q1 , q2 ,..., qn .
В силу принципа суперпозиций напряженность поля системы зарядов
E
Ei .
i
Поэтому
EdS
Ei dS
S
S i
1
Ei dS
qi .
i
S
0
i
17.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Следовательно
Теорема Гаусса
1
EdS
S
0
q .
i
i
Поток вектора напряженности электрического поля через
замкнутую
поверхность
равен
алгебраической
сумме
заключенных внутри этой поверхности зарядов, деленной на ε0.
При переходе от системы зарядов к непрерывному их распределению в
объеме V, окруженному замкнутой поверхностью S, заменим qi dq.
Введем характеристику распределения зарядов –
объемную плотность зарядов ρ(x,y,z) = dq/dV. Тогда
Окончательно
1
EdS ( x, y, z )dV .
S
0 V
i
dq ( x, y, z )dV .
V
Теорема Гаусса
в интегральной форме.
Теорема Гаусса позволяет, в ряде случаев, найти напряженность поля более
простыми средствами, чем с использованием формулы для напряженности точечного
заряда и принципа суперпозиции полей.
18.
ЭЛЕКТРОСТАТИКАЭлектрическое
поле
.
Для потока вектора E установим одно полезное соотношение.
Пусть dS представляет куб со сторонами dx, dy, dz,
ориентированными вдоль осей х, у, z.
Поток через
поверхность (1) dS = dydz грани 1 куба равен
Теорема Гаусса
x, y dy, z
4 E
dy
n
x, y , z
dx
1
x, y, z dz
dz
3
6
( EdS )1 ( Ex nx E y n y Ez nz )dydz Ex dydz.
5
n
E На грани 1 вектор сориентирован против оси х
(nx = 1, ny = 0, nz = 0).
n Поток через грань 2 равен (nx = +1, ny = 0, nz = 0)
x dx, y, z
2
E x
( EdS ) 2 E x ( x dx, y, z )dydz E x
dx dydz.
x
Складывая потоки сквозь грани 1 и 2, получаем поток
через грани 1 и 2 наружу
E x
( EdS )1 2
dxdydz.
x
19.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Проведя аналогичные вычисления для граней 3, 4
Теорема Гаусса
E y
E y
( EdS )3 4 E y dxdz E y
dy dxdz
dxdydz
y
y
и граней 5, 6
E z
E z
( EdS ) 5 6 E z dxdy E z
dz dxdy
dxdydz,
z
z
получаем поток через все грани бесконечно малого куба (dV = dxdydz)
E
E y Ez
dV ( E )dV .
( EdS ) x
y
z
x
Если поверхность S, ограничивающая векторное поле E , замкнута и
конечна и конечен объем V, ограничиваемый этой поверхностью, то, разбивая
этот объем на бесконечно малые объемы dV (на соседних соприкасающихся
гранях потоки взаимно компенсируются в силу противоположного направления
нормалей), получаем для полного потока вектора через замкнутую поверхность S
EdS ( E )dV .
S
V
20.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Теорема Гаусса
Скалярное
произведение оператора-набла
на векторную функцию
E называется дивергенцией вектора E
Ex E y Ez
divE.
( E )
y
z
x
Таким образом
( x, y, z )
EdS ( E )dV divEdV
dV .
S
V
V
V
0
В последних двух равенствах интегрирование идет по одному объему, откуда
следует, что подинтегральные функции равны. Следовательно
1
div E
( x, y , z ).
0
Теорема Гаусса
в дифференциальной форме
Дифференциальная форма теоремы Гаусса позволяет рассчитать
электрическое поле при произвольном пространственном распределении зарядов.
21.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Расчет поля бесконечной равномерно заряженной
плоскости с поверхностной плотностью σ
Расчет полей с помощью
теоремы Гаусса
EdS EdS EdS EdS
n
E
S1
n
S
S2
n
q
S3
S1
S2
S3
1
E 2 EdS 2 EdS 2ES1, 2 q.
S1, 2
Тогда
S1, 2
E
0
1 q
.
2 0 S1, 2 2 0
Если плоскость окружает среда с относительной диэлектрической
проницаемостью ε, то
Поле бесконечной равномерно
E
.
заряженной плоскости является
2 0
однородным.
Поле плоскости конечных размеров является неоднородным, возникают
краевые эффекты.
22.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Расчет поля двух параллельных бесконечных плоскостей равномерно
заряженных с разноименной поверхностной плотностью σ.
+σ
E
E
-σ
Для простоты, применим в данной задаче
принцип суперпозиций
E
I
II
III
E
E
E
E E E .
Сложение полей проведем вдоль направления
оси х.
Плоскости делят пространство на 3 области.
Сложение полей проведем в каждой из них.
Е
0
I. E E E
0
х
II. E E E
0.
2 0 2 0
.
2 0
2 0
0
III. E E E
0.
2 0
2 0
23.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Работа
по переносу заряда в
электрическом поле
F
q0 q
A Fdr q0 Edr
4 0
q0
r1
q
r2
Рассмотрим работу по переносу пробного заряда q0
в поле точечного заряда q.
0
4 0
q0 q
r dr
r 3 4 0
r2
rdr
r r 3
1
r2
q 0 q 1 q0 q 1
dr
r r 2 4 0 r1 4 0 r2 U (r1 ) U (r2 ).
1
Работа зависит только от положения тела в
начале (r1) и в конце (r2) пути, но совершенно
не зависит от траектории перемещения тела
из точки r1 в точку r2.
F
Электростатическое поле является потенциальным.
24.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Потенциальная энергия определяется с точностью до
Потенциальная энергия произвольной постоянной.
Пусть при
r2 , U 2 0.
Тогда
r1 r, U1 U .
Потенциальная энергия взаимодействия
точечных зарядов равна
U
0
U
q q0
.
4 0 r
1
Для одноименных зарядов
r
Энергия взаимодействия системы n
точечных зарядов может быть записана в
симметричной форме:
Для разноименных зарядов
1 n qk qi
U
, k i.
2 k ,i 1 4 0 rki
Множитель 1/2 перед знаком суммы
учитывает тот факт, что в эту сумму энергия
каждой пары зарядов входит дважды.
25.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Электрический
потенциал
Потенциал электрического поля φ является энергетической
характеристикой поля.
Потенциал - это физическая величина численно равная
потенциальной энергии единичного положительного
точечного заряда, переносимого из бесконечности в
данную точку поля.
U
.
q0
Отсюда следует, что потенциал поля созданного точечным зарядом q,
определяется выражением
1 q
4 0 r
.
Используя связь между потенциальной энергией и работой, определим
потенциал через работу.
Потенциал - это физическая величина численно равная
работе по перемещению единичного положительного
точечного заряда, из данной точки поля на бесконечность.
A
.
q0
26.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Работа зависит только от положения тела в начале (r1)
Электрический
и в конце (r2) пути, но совершенно не зависит от траектории
потенциал
перемещения тела из точки r1 в точку r2.
В результате величина А1,2 может быть выражена в виде разности двух чисел
φ1 и φ2 – потенциалов электрического поля в точках r1 и r2 :
q
q
q0 1 2 .
A1, 2 q0 Edr q0
4 0 r1 4 0 r2
r1
r2
Данная формула используется для введения внесистемной единицы энергии,
очень удобной при рассмотрении движения объектов в микромире: в атомной,
ядерной физике и физике элементарных частиц.
Количество энергии, сообщаемой электрону (или другой частице с тем же
зарядом) при перемещении в электрическом поле между точками с разностью
потенциалов 1 В. Действующее на частицу электрическое поле увеличивает ее
кинетическую энергию на величину в 1 электронвольт.
K = U = e .
1 эВ = (1,6 10 19 Кл) (1 В) = 1,6 10 19 Дж.
27.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Связь между напряженностью и
потенциалом электрического поля.
В интегральной форме эта связь следует из
предыдущей формулы:
1 2 Edr .
2
Отсюда следует очень важное свойство
постоянного
электрического
поля
–
циркуляция напряженности электрического
поля по замкнутому контуру равна нулю.
1
Edr 0.
Соотношение между силой и потенциальной энергией позволит нам найти
связь в дифференциальной форме:
F U . F q0 E, U q0 . q0 E q0 .
Окончательно
Из этой формулы следует одно важное
E . соотношение.
Согласно теореме Стокса, присутствует следующая связь между контурным и
поверхностным интегралами:
Edr rot EdS 0,
S
где контур ℓ ограничивает поверхность S, ориентация которой определяется
направлением вектора положительной нормали n.
28.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
rotE 0.
Следовательно
Безвихревой характер
электростатического поля
rotE
называется ротором или вихрем и является векторным произведением
оператора «набла» и векторной
функцией
(вектор напряженности
rotE [ E ].
электрического поля)
Из условия E и следует важное соотношение,
а именно величина векторного
произведения [ E ] для стационарных электрических полей
всегда равна нулю.
Действительно, по определению, имеем
i
[ E ]
j
k
i
j
x y z
x
x y z
x
y
y
k
0,
z
z
поскольку определитель содержит две одинаковые строки. Следовательно
электростатическое поле имеет безвихревой характер.
29.
ЭЛЕКТРОСТАТИКАЭлектрическое поле
Эквипотенциальными поверхностями называются поверхности
φ(x,y,z)=const и предназначены для
Эквипотенциальные равного потенциала
наглядного (графического) представления энергетических
поверхности
характеристик электрического поля в пространстве.
Через равные приращения потенциала Δφ чертят эквипотенциальные
поверхности, а затем для полноты картины проводят силовые линии,
перпендикулярные эквипотенциальным поверхностям.
Там, где расстояние между эквипотенциальными поверхностями мало,
напряженность поля велика и наоборот.
30.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в веществе
Электрическое поле
в проводниках
Изучить самостоятельно.
Диэлектриками (или изоляторами) называются вещества не
способные проводить постоянный электрический ток.
Идеальных изоляторов не существует. Все вещества, хотя бы в
ничтожной степени, проводят электрический ток.
Однако, вещества, называемые диэлектриками, проводят постоянный ток в
1015-1020 раз хуже, чем вещества, называемые проводниками.
Более точное разделение вещества на проводники, полупроводники и
диэлектрики проведем позднее – в квантовой физике.
Слабая электропроводность диэлектриков связана с тем, что в них
отсутствуют свободные носители зарядов – все заряды в диэлектриках жестко
связаны друг с другом. То есть электроны в диэлектриках не обобществлены, а
принадлежат отдельным атомам.
Внешнее электрическое поле Е0 лишь слегка смещает центр тяжести
атомных ядер. Происходит поляризация диэлектрика.
Молекулы становятся электрическими диполями, ориентированными
положительно заряженными концами в направлении электрического поля.
Само смещение зарядов диэлектрика в разные стороны называется
электрической поляризацией.
Электрическое поле
в диэлектриках
31.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в диэлектриках
Заряды,
появляющиеся
в
результате
поляризации,
называют
индукционными или связанными.
В объеме однородного диэлектрика поляризационные заряды взаимно
компенсируются, и заряд остается нескомпенсированным лишь на поверхности
диэлектрика.
Полная поляризуемость диэлектрика включает составляющие –
электронную, ионную и ориентационную (дипольную).
32.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в диэлектриках
Электронная поляризуемость обусловлена смещением электронной оболочки
атома относительно ядра.
Ионная поляризуемость вызвана смещением заряженных ионов по
отношению к другим ионам.
Ориентационная (дипольная) поляризуемость возникает, когда вещество
состоит из молекул, обладающих постоянными электрическими дипольными
моментами, которые могут более или менее свободно изменять свою ориентацию во
внешнем электрическом поле.
Поэтому диэлектрик в электрическом поле можно представить себе
состоящим из системы диполей (двойной электрический полюс).
Диполь характеризуется
величиной, называемой
q
q
моментом диполя p ql .
l
+
Вектора момента диполя направлен от отрицательного
заряда к положительному.
В отсутствии внешнего электрического поля молекулы диэлектриков
разделяются на неполярные и полярные молекулы.
Неполярные молекулы не обладают собственным дипольным моментом в
отсутствии внешнего электрического поля. Это симметричные молекулы О2, N2.
Это связано с тем, что центры тяжести положительных и отрицательных
зарядов совпадают l = 0.
33.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в диэлектриках
У несимметричных молекул, таких как H2O, HCl и др., центры тяжести
положительных и отрицательных зарядов не совпадают, поэтому эти молекулы
обладают собственным дипольным моментом в отсутствии внешнего поля.
Такие молекулы называются полярными.
Для количественного описания поляризации
диэлектриков вводится
понятие вектора поляризации, или поляризованность P.
Вектором поляризации называют суммарный дипольный момент молекул
диэлектрика в единице объема диэлектрика при его поляризации.
1
P
V
p
i.
i
Для сплошной среды перейдем к интегралу, в изотропных условиях
ненулевой вклад в этот интеграл дают заряды, сосредоточенные на поверхности
диэлектрика:
1
P
V
P
ср
dV .
V
Здесь Pср pn, где Pср – средний дипольный момент единицы объема,
направленный
вдоль
вектора
электрического
поля;
n – концентрация молекул; p – средний дипольный момент одной молекулы.
34.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в диэлектриках
+ + + S
l ,P
Eпол
E
+σпол
-σпол
+ -
-σсвоб
+σсвоб
Если поместить диэлектрик в однородное электрическое поле E0 ,
то на поверхности диэлектрика появятся поляризационные заряды с поверхностной
плотностью пол.
Пусть
S – площадь основания параллелепипеда.
l – вектор, проведенный от отрицательного к
E0
положительному основанию.
Вектор поляризации диэлектрика, по определению, будет
равен
пол Sl
+ P
.
+
V
Величина
объема параллелепипеда равна V S ( n l ),
+
где n вектор нормали, проведенной к основанию
+ -
+ + -
положительно заряженного основания параллелепипеда.
Используя данное соотношение, получим
n
( Pn ) S (n l ) пол S (n l ),
пол ( Pn ).
Последнее равенство справедливо для поверхности диэлектрика любой формы.
35.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в диэлектриках
Полный поляризационный заряд в объеме диэлектрика при неоднородной
поляризации равен поверхностному поляризационному заряду с обратным знаком
qпол
полdS ( PdS ) divPdV .
S
С другой стороны,
S
qпол полdV .
V
V
Откуда получаем соотношение между
плотностью поляризационного заряда и
вектором поляризации
divP пол .
Если поляризация неоднородна, ее дивергенция определяет появляющуюся в
материале результирующую плотность зарядов.
Эти заряды формируют вполне реальные заряженные области в объеме
диэлектрика в присутствии внешнего электрического поля, но исчезают в отсутствие
внешнего поля.
Величина напряженности поля в однородном поляризованном диэлектрике
равна, согласно теореме Гаусса,
св об пол
E
n.
0
36.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в диэлектриках
Для большинства диэлектриков в широком интервале величин E
справедлива линейная зависимость, выражаемая
веществ и
для изотропных
кристаллов с кубической решеткой соотношением P E.
0
Коэффициент пропорциональности κ (каппа) называется диэлектрической
восприимчивостью диэлектрика.
P
В результате получим
своб
пол
своб
E
n
n E0 E.
0
0
0
Отсюда поле в диэлектрике равно
своб 1
1
E
E
n
E0
0.
0 1
1
Величина = (1 + κ) называется относительной диэлектрической проницаемостью
среды и характеризует электрические свойства диэлектрика.
Уравнения электростатики Одно из основных уравнений электростатики
сформулировано в виде теоремы Гаусса, которая в
для диэлектриков
дифференциальной
форме
связывает
величину
напряженности электрического поля с плотностью его
источников – электрических зарядов :
div E
.
0
37.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в диэлектриках
Разделим полную плотность зарядов ρ на две
–
плотность
свободных
и
Уравнения электростатики составляющие
поляризационных электрических зарядов:
для диэлектриков
= своб + пол.
Поляризационные заряды появляются за счет неоднородной поляризации, а
остальные заряды являются свободными. Обычно свободные заряды распределены
на проводниках или размещены известным образом в пространстве.
Уравнение поля для диэлектрика в результате принимает вид
св об пол
divP
divE
св об
.
0
0
Собирая величины Е и P под знаком дивергенции, запишем
Введем новый вектор
div( 0 E P) своб.
D 0 E P, называемый вектором электрической
индукции.
С использованием D основные уравнения электростатики для диэлектриков
примут вид
Уравнение для ротора не изменилось, то есть и в
divD св об ;
rotE 0.
диэлектриках поле безвихревое.
38.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в диэлектриках
С другой стороны D 0 E P 0 E 0 E (1 ) 0 E 0 E.
Данное равенство справедливо для изотропных сред и, по существу,
описывает свойства вещества в электрическом поле.
Смысл введения вектора электрической индукции состоит в
Теорема Гаусса
том, что поток вектора D через
любую
замкнутую
для диэлектриков
поверхность определяется только свободными зарядами
qсв об
DdS ,
S
а не всеми зарядами внутри объема, ограниченного данной поверхностью, подобно
потоку вектора E.
Это позволяет не рассматривать поляризационные заряды и упрощает
решение многих задач.
Твердые диэлектрики.
Твердые диэлектрики обладают рядом интересных и
Электреты. Пьезоэлектрики. практически важных особенностей.
Одна из них связана с наличием у ряда веществ постоянной поляризации,
даже в отсутствие внешнего электрического поля.
Спонтанная поляризация является результатом несовпадения «центров тяжести»
положительных и отрицательных зарядов и может быть получена искусственно.
39.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в диэлектриках
Так, если растопить воск и поместить его в электрическое поле, то в
процессе затвердевания дипольные моменты его молекул окажутся частично
ориентированными по полю и останутся в таком положении в затвердевшем
материале после снятия поля.
Вещество, обладающее поляризацией в отсутствие внешнего электрического поля,
называется электретом. Электреты – электрические аналоги постоянных магнитов.
Однако свободные поляризационные заряды на поверхности электрета достаточно
быстро нейтрализуются молекулами воздуха. Электрет «разряжается» и не создает
заметного внешнего поля.
Изменение поляризации в диэлектриках может происходить и под действием
механических напряжений, например при сгибе кристалла или при его сжатии и
растяжении.
Наблюдаемый при этом слабый электрический эффект называется прямым
пьезоэлектрическим эффектом.
Пьезоэлектрическими свойствами обладают только ионные кристаллы.
Если кристаллические решетки положительных и отрицательных ионов
таких кристаллов при внешнем воздействии деформируются по-разному, то в
противоположных местах на поверхности кристалла выступают электрические
заряды разных знаков и наблюдается пьезоэлектрический эффект.
Важнейшим пьезоэлектриком является кварц. В нем можно возбудить поле
6
до 3 10 B/м.
40.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в диэлектриках
Сегнетоэлектрические
кристаллы
41.
ЭЛЕКТРОСТАТИКАЭлектрическое поле в проводниках
42.
ЭЛЕКТРОСТАТИКАЭлектроемкость
43.
ЭЛЕКТРОСТАТИКАЭнергия электрического поля
44.
ЭЛЕКТРИЧЕСКИЙ ТОКПерейдем теперь к движущимся зарядам
Электрический ток представляет собой упорядоченное (направленное)
движение электрически заряженных частиц или заряженных макроскопических тел.
За направление тока условно принято направление движения
положительных зарядов.
Сила тока определяется как количество заряда, проходящего через
Сила тока
выделенную поверхность в единицу времени:
i
dq
.
dt
Если dq/dt = const, то такой ток принято называть постоянным и
обозначать буквой I. Если ток меняется со временем, т.е. dq/dt const, то он
называется переменным и обозначается буквой i.
Плотность С током непосредственно связана плотность тока.
тока
Выделим
в проводящей среде бесконечно малый объем и обозначим
через u средний вектор скорости направленного движения зарядов е
в данном объеме, объемная плотность которых равна = ne, где n концентрация
зарядов; е величина одного заряда. Обозначим плотность тока вектором j ,
определяющим количество зарядов, проходящих в единицу времени через единичную
площадку, перпендикулярную потоку заряженных частиц:
j u enu.
45.
ЭЛЕКТРИЧЕСКИЙ ТОКУмножив
плотность тока на величину площадки S, перпендикулярную
вектору j , получим ток
I ( j , Sn ) ( j , S ),
где n – единичный положительный вектор нормали к поверхности S.
Если в пределах поверхности S плотность тока меняется, то
I
j dS .
S
Закон сохранения
заряда
Количество зарядов q, переносимых через элемент поверхности
dS за время t, равно
q (u n )dS t.
Знак «минус» указывает, что заряд уходит через поверхность dS. Заряд, проходящий
через замкнутую поверхность S в единицу времени, равен
q
(u , dS ) j dS .
t
S
S
Символ частной производной отмечает тот факт, что поверхность S остается
неподвижной.
Рассмотрим левую и правую часть этого равенства.
46.
ЭЛЕКТРИЧЕСКИЙ ТОКПолный заряд под поверхностью S
q
dV
V
равен интегралу от плотности электрического заряда , находящегося в объеме V,
ограниченном поверхностью S.
Изменение заряда равно
q
dV .
t
t
V
Поверхностный интеграл от плотности тока может быть с помощью теоремы
Остроградского выражен через объемный интеграл:
S
j dS divj dV .
V
В результате для произвольного объема V получим
div
j dV 0,
V t
это возможно лишь при условии
divj
.
t
Это
уравнение
называется
уравнением
непрерывности и выражает закон сохранения
заряда .
47.
ЭЛЕКТРИЧЕСКИЙ ТОКЗакон сохранения заряда выражает тот фундаментальный факт
классической электродинамики, что электрический заряд неуничтожим, он никогда
не теряется и не создается.
Электрический заряд перемещается с места на место, пересекает границы
некоторых выделенных объемов, но никогда не возникает из ниоткуда и не исчезает
иначе, как только выйдя из объема. Заряд сохраняется.
Если токи стационарны (постоянны), т.е. не зависят от времени, то
Постоянный
div j 0 и для замкнутой поверхности имеем
ток
j dS 0.
S
Разомкнув поверхность S, получаем, что в случае стационарных токов сумма
токов, проходящих через замкнутую поверхность, равна нулю:
I
k
k
k
j dS 0.
Sk
Стационарность токов означает, что плотность электрических зарядов в
каждой точке пространства не изменяется со временем, хотя и происходит движение
электричества,
но на место уходящих зарядов непрерывно поступают новые.
Так как div j 0, то j не имеет источников, а это значит, что линии постоянного тока
нигде не начинаются и нигде не заканчиваются.
Линии постоянного тока всегда замкнуты.
48.
ЭЛЕКТРИЧЕСКИЙ ТОКЗаконы постоянного тока
Возбуждение и поддержание электрического тока в проводниках
возможно при наличии в них электрического поля.
Немецкий учитель физики Георг Ом установил, что сила тока в проводнике
пропорциональна разности потенциалов 1 2 = U у начала и конца этого
проводника, считая по направлению тока,
Закон Ома
I
1 2
R
U
.
R
Величина
R
называется
электрическим
сопротивлением
или
просто
сопротивлением определенного участка этого проводника.
Считается, что ток идет от участка с большим потенциалом к меньшему
( 1 > 2), т.е. по направлению движения положительных зарядов.
Электрическое сопротивление характеризует противодействие проводника
или электрической цепи электрическому току.
Для однородного по составу цилиндрического проводника можно записать
R = ρl/S, где l длина участка проводника, обладающего сопротивлением R; S
площадь поперечного сечения проводника; удельное сопротивление,
характеризующее вещество проводника.
Вместо можно ввести обратную ему величину = 1/ , называемую
удельной проводимостью или электропроводностью.
Электропроводность характеризует способность
электрический ток под действием электрического поля.
вещества
пропускать
49.
ЭЛЕКТРИЧЕСКИЙ ТОКЗаконы постоянного тока
Вольтамперная
характеристика
проводника
Прямая пропорциональная связь
между током и напряжением
приводит к линейной зависимости
вольтамперной характеристики
проводников.
I
0
U
Зависимость
Удельное сопротивление металлов линейно растет с
сопротивления температурой: = 0(1 + t), где , 0 – удельные сопротивления
металлов
при t и 0 С; t – температура в градусах Цельсия; –
от температуры температурный коэффициент сопротивления.
ρ
Линейная зависимость сопротивления
металлов от температуры нарушается
при сверхвысоких и сверхнизких
температурах.
ρ0
Особое значение эта зависимость имеет
при сверхнизких температурах, когда
- 273
0
t, °C появляется сверхпроводимость.
Сопротивление металла скачком становится равным нулю.
Явление сверхпроводимости имеет квантовую природу и проявляется не
только в металлах.
Высокотемпературная сверхпроводимость.
50.
ЭЛЕКТРИЧЕСКИЙ ТОКЗаконы постоянного тока
Закон Ома может быть выражен в локальной
Закон Ома
(дифференциальной) форме.
в дифференциальной
Разность потенциалов, входящую в закон Ома, можно
форме
выразить через линейный интеграл от напряженности поля E ,
взятый от начального до конечного сечения рассматриваемого участка проводника:
2
E, d l
1 2 Edl U12 .
dI j, d S
1
dl / dS
Применим закон Ома для бесконечно малого цилиндрического участка
проводника с боковыми гранями, перпендикулярными вектору плотности
электрического тока.
dS
Имеем в этом случае
dl
dU
( E , dl )
( E , dl )
dI
(
j
,
d
S
)
.
R
R
(dl / dS )
n
j, E
Поскольку все векторы параллельны, то из этого
соотношения следует
j E
- закон Ома в дифференциальной форме.
Эта формулировка наиболее проста и вместе с тем является наиболее общей.
В такой формулировке устанавливается связь между величинами, относящимися к
одной определенной точке проводника.
51.
ЭЛЕКТРИЧЕСКИЙ ТОКЗаконы постоянного тока
Если ток стационарный, то, по определению,
для таких токов
Закон Ома
выполняется условие / t divj 0.
в дифференциальной
Последнее равенство можно переписать в виде div E div D / 0.
форме
Для однородной среды ( = const, = const) получаем divD 0.
div
D
0 в случае стационарных токов
С учетом теоремы Гаусса имеем
макроскопические электрические заряды могут находиться только на поверхности
или в местах неоднородности проводящей среды.
В этом состоит аналогия между полем стационарных токов и
электростатическим полем.
Заряды, создающие стационарные токи, порождают в окружающей среде
кулоновское поле, такое же, как и неподвижные заряды той же плотности.
Поэтому электрическое поле стационарных токов потенциально.
Но, в отличие от кулоновского поля, поле стационарных токов существует
внутри проводников, иначе бы не было и токов.
Силовые линии электростатического поля всегда нормальны к поверхности
проводника, что не обязательно выполняется для поля стационарных токов.
Возникает вопрос, какие силы поддерживают стационарные токи?
52.
ЭЛЕКТРИЧЕСКИЙ ТОКЗаконы постоянного тока
Если бы все действующие в цепи электродвижущие силы
Сторонние
сводились к кулоновским силам, то, двигаясь свободно в
электродвижущие силы
проводнике, разноименные заряды очень быстро бы
нейтрализовались и разность потенциалов, а вместе с этим и ток исчезли.
Поэтому для поддержания постоянного поля токов в цепи требуется наличие
поля сил неэлектростатического происхождения.
Для поддержания поля токов необходимы непрерывные затраты энергии,
которые не дают электростатические поля, так в них не происходит
взаимопревращений энергии.
Энергия, выделяющаяся в цепи тока, должна непрерывно компенсироваться
за счет иных видов энергии механической, химической, тепловой, световой и
прочих источников сил неэлектростатического происхождения.
Эти силы называются сторонними (электростатическому полю) - Fстор , а их
напряженность сила, действующая на единичный положительный заряд, Eстор .
При одновременном действии электростатического поля и поля сторонних
сил в проводнике возникает ток с плотностью
j ( E Eстор ).
53.
ЭЛЕКТРИЧЕСКИЙ ТОКЗаконы постоянного тока
Пусть источником (тока) сторонних сил будет гальванический
элемент, обозначаемый в цепи вертикальными линиями «плюс» – длинная, тонкая, «минус» – короткая, толстая.
Подсоединим к источнику тонкие однородные
проводники, общее сопротивление которых R,
I
φ1
φ2
R
обозначим на схеме прямоугольником.
- +
Выделим на схеме точки 1 и 2, потенциалы
1
3
4
2
которых φ1 и φ2, точки 3 и 4, отделяющие
источник от остальной цепи. Замкнем
К
схему
проводниками с ключом К, который вначале
разомкнут.
1 I
Плотность тока в цепи j =I/S. Тогда, согласно закону Ома, имеем E Eстор
.
S
Умножим это соотношение на элемент длины провода dl и проинтегрируем
по участку проводника от точки 1 до точки 2:
Электродвижущая
сила.
ЭДС
2
2
1
1
2
dl
IR12 .
S
1
Edl Eсторdl I
Поле стационарных токов потенциально, и первый интеграл равен разности
потенциалов 1 2 на рассматриваемом участке цепи 1 3 4 2.
Второй интеграл отличен от нуля лишь на участке 3 4, где есть источник
сторонних сил, т.е. гальванический элемент.
54.
ЭЛЕКТРИЧЕСКИЙ ТОКЗаконы постоянного тока
В области, где действуют сторонние силы, поле Естор
Электродвижущая потенциально и интеграл не зависит от прохождения пути
сила.
интегрирования через гальванический элемент.
ЭДС
Значение этого интеграла характеризует свойства самого
элемента и называется электродвижущей силой (ЭДС) элемента
2
4
1
3
E Eсторdl Eсторdl.
Таким образом, при наличии в разомкнутой цепи ЭДС можем записать
уравнение, определяющее величину тока на неоднородном участке цепи 1 3 4 2
(обобщенный закон Ома):
1 2 + E = IR12.
Под R12 = R + r подразумевается сопротивление всего участка цепи, включая
сопротивление гальванического элемента r.
Частным случаем полученного обобщенного закона Ома является исходное
соотношение 1 2 = IR для однородного участка цепи, не содержащего ЭДС (E = 0).
Если цепь замкнута (ключ К замкнут, 1 2 = 0) и ток лишен
разветвлений,
то интегрирование по всей замкнутой цепи 1 3 4 2 1 дает IR12 Edl Eсторdl.
l
Так как Edl 0, то получим закон Ома для полной цепи I(R+r) = E.
55.
ЭЛЕКТРИЧЕСКИЙ ТОКЗаконы постоянного тока
Закон
Джоуля Ленца
56.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Всякая реальная электрическая цепь представляет собой
Колебательный колебательный контур, состоящий из распределенных по всей цепи
контур
параметров: сопротивления, емкости и индуктивности.
Распределенные параметры представим себе – локальными, пренебрегая
соответствующими параметрами подводящих проводов.
Рассмотрим электрическую цепь (электрический контур), состоящую из
сопротивления R, катушки индуктивности L, конденсатора С и генератора E(t).
Такая цепь называется электрическим
R
колебательным контуром.
Запишем закон Ома для этой цепи
~
L
-q
+q
C
E(t)
IR 1 2 EL E (t ),
где φ1 - φ2 – разность потенциалов
конденсаторе, EL – ЭДС самоиндукции.
на
dI
d 2q
Так как 1 2 q / C , EL L
L 2 ,
dt
dt
То закон Ома запишем в виде
d 2q
dq
1
L
R
q E (t ).
2
dt
C
dt
57.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Процессы в электрическом колебательном
Уравнение колебательного
контуре описываются уравнением, называемым
контура
уравнением колебательного контура
d 2q
dq
1
2
2
q
E (t ).
0
dt 2
dt
L
Здесь 2
R
1
, 02
.
L
LC
Такие колебания реализуются, если в контуре нет
Незатухающие
генератора и омическое сопротивление R = 0.
свободные колебания
Этот электрический аналог контура описывается уравнением
L
d 2q
2
0 q 0.
2
dt
Решением этого уравнения является функция, которая, будучи
дважды продифференцированной, перейдет вновь в себя,
изменив знак и приобретя некоторый множитель.
C
Такими функциями являются Acos( 0t + ), Asin( 0t + ), Aei(ωt+φ) и их линейные
комбинации. Но фактически это все одна функция, поскольку косинус всегда можно
свести к синусу cos = sin( + /2), а синус может быть выражен через экспоненты с
мнимым показателем:
1 i
sin
e e i .
-q
+q
2i
58.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Домножим уравнение, описывающее изменение заряда в колебательном
контуре, на dq/dt и преобразуем его к виду
2
dq d 2 q
dq
d 1 dq
02 q 2
2
0 q
0.
dt dt 2
dt
dt
2
dt
2
Откуда следует, что величина, стоящая в квадратных скобках, не изменяется
2
со временем:
где q – константа (максимальный
dq
2 2
2 2
0
0 q 0 q0 , заряд на обкладках конденсатора).
dt
Если переписать это уравнение в виде (ω02 = 1/LC, I = dq/dt)
LI 2
q2
q02
const ,
2
2C
2C
то оно приобретает вид закона сохранения энергии: в колебательном контуре без
активного сопротивления сумма энергий электрического q2/2C и магнитного LI2/2
полей, запасенных в конденсаторе и катушке индуктивности, остается постоянной.
2
dq
2
2
2
Преобразуем полученное уравнение к виду
0 q0 q , откуда получаем
dt
dq
0dt. После интегрирования находим arccos q t .
2
2
0
q0 q
q
0
Следовательно, решение исходного уравнения, описывающего колебания
заряда в LC-контуре, имеет вид q = q0cos(ω0t +φ).
59.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Зная зависимость заряда на обкладках конденсатора от времени q(t), можно
найти все характеристики системы ток, разность потенциалов на обкладках
конденсатора, электрическую и магнитную энергии:
dq
I
q0 0 sin 0t q0 0 cos 0t - ток опережает заряд по фазе на π/2.
dt
2
q q0
Разность потенциалов на обкладках
1 2
cos 0t .
конденсатора меняется в одной фазе с
C
C
изменением заряда
Электрическая Wq и магнитная Wm
энергии в контуре равны
q02 1 cos 2 0 2
q2
Wq
,
2C
2C
2
L 02 q02 1 cos 2 0 2
LI 2
Wm
.
2
2
2
Изменения электрической и магнитной энергий происходит с удвоенной частотой 2 0
по сравнению с частотой 0 изменения заряда, тока и разности потенциалов.
При достижении электрической энергией максимума магнитная энергия
равна нулю и наоборот. Говорят, что величины Wm и Wq колеблются в противофазе.
Сумма этих энергий постоянна:
Wq Wm
Период свободных колебаний T0 2 2 LC
0
q02
LI02
.
2C
2
- формула Томсона.
60.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Свободные
Если подводящие провода и катушка индуктивности собраны
затухающие не из сверхпроводящих материалов, то колебательный контур всегда
колебания обладает сопротивлением R. Проходя по такой цепи, ток выделяет
джоулево тепло, расходуя энергию, первоначально запасенную в колебательной
системе.
R
Колебания в такой системе описываются
уравнением, аналогичным незатухающим, но с
добавлением слагаемого, описывающего потери
энергии на сопротивлении R:
L
d 2q
dq
-q
+q
C
где
02
2
dt 2
2
dt
02 q 0.
Решение этого уравнения q q0e
1
R2
.
LC 4 L2
Период затухающих колебаний равен
T
2
2
2
0
2
t
T0
1
Напряжение на конденсаторе равно
U C 1 2
cos t ,
02
2
T0
q q0 t
e
cos 0t U 0C e t cos 0t .
C
C
Напряжение на конденсаторе совпадает по фазе с зарядом.
2
0
.
61.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Свободные Сила тока в этом контуре меняется по закону
затухающие
dq
колебания
I
q e t cos t q e t sin
dt
0
Тогда
2 2
t
t
2 2 02 0 .
cos t
sin t .
2
2
2
2
Введем угол ψ, определяемый условиями: cos
sin
0
q0e t cos t sin t .
Умножим и разделим последнее выражение на
I 0 q0e
,
0
2
2
0
и
2
2
так как cos sin 1.
I 0 q0e t cos cos t sin sin t
0 q0e t cos t I 0e t cos t , I 0 0 q0 .
62.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Свободные
затухающие
колебания
Поскольку cosψ < 0, а sinψ > 0, то ψ лежит в интервале π/2 < ψ < π.
ψ
0
Таким образом, при наличии в контуре R сила
тока в цепи опережает напряжение на
конденсаторе более чем на π/2 (при R = 0 –
опережение равно π/2).
колебаний
характеризуется
логарифмическим
Логарифмический Затухание
декрементом затухания , равным натуральному логарифму
декремент
отношения амплитуд колебаний, отличающихся по времени
затухания
измерения на период
q0e t
A(t )
ln
ln
T .
( t T )
A(t T )
q0e
Время , по истечении которого амплитуда колебаний убывает в е раз,
называется временем затухания: = 1/β. За время система совершит N полных
колебаний, где N = τ/T = 1/βT.
Таким образом, логарифмический декремент затухания связан с числом
колебаний N, приводящим к уменьшению амплитуды в е раз соотношением λ = 1/N.
R 2
R
R
С другой стороны
T
.
2L
L
L
1
R2
LC 4 L2
63.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Логарифмический
декремент
затухания
Если затухание невелико β2 << ω02, тогда ω ≈ ω0 и
R
C
R
.
L 0
L
Важнейшей характеристикой колебательного
Добротность добротность
Q,
величина,
обратно
контура
логарифмическому декременту:
Q
контура является
пропорциональная
N .
Чем выше добротность, тем большее число колебаний успеет совершить
система, прежде чем амплитуда колебаний уменьшится в е раз. При слабом затухании
1 L Величину Q можно связать с относительным изменением энергии W в
Q
.
в
контуре
R C колебательной системе за период. Энергия 2
пропорциональна квадрату амплитуды тока или заряда W q . Относительное
изменение энергии за период равно
W W (t ) W (t T ) (1 e 2 T ) A2 (t )
1 e 2 T .
2
W
W (t )
A (t )
При слабом затухании , разложив экспоненту в ряд еx 1 + x и
выразив логарифмический декремент = через добротность Q, находим
добротность тем выше, чем меньше
W
2
2
относительные потери энергии в контуре за
1 e 2 2 . Q
W
Q
( W / W ) период.
64.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
В случае сильного затухания β2 >> ω02, вместо колебаний происходит
Свободные
апериодический разряд конденсатора.
затухающие
Сопротивление контура, при котором колебательный процесс
колебания
переходит в апериодический, называется критическим
Rк2
1
L
2
2
0 ,
,
R
2
.
к
2
4L
LC
C
Вынужденные колебания в контуре, состоящем из сопротивления R,
Вынужденные
емкости С, индуктивности L возникают, если эта цепочка
электрические
подключена к источнику электродвижущей силы E(t), величина
колебания
которой меняется со временем t .
Уравнение колебательного контура
R
d 2q
dq
1
2
2
q
E (t ).
0
dt 2
dt
L
~
L
-q
+q
C
E(t)
Функцию E(t) представим в виде E(t) = E0cosωt,
тогда d 2 q
dq
1
2
dt
2
2
dt
0 q
L
E0 cos t ,
где ω – частота внешней вынуждающей силы.
65.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Общее решение этого неоднородного уравнения можно представить
Вынужденные в виде суммы общего решения однородного уравнения (затухающие
электрические колебания) и любого частного решения q(t) исходного неоднородного
колебания
уравнения. Периодическую функцию cos t заменим в этом
уравнении на функцию комплексного переменного ei t:
E0 i t
d 2q
dq
2
2
q
e ,
0
2
dt
dt
L
поскольку вещественная часть ei t, а только вещественная величина имеет
физический смысл, равна cos t.
Будем искать частное решение этого уравнения в виде q(t) = q0e i t.
Подставив это выражение в неоднородное уравнение, продифференцировав
его по t и сократив на ei t, находим
E0
i t
q
(
t
)
e
.
q0
,
2
2
2
2
L 0 i 2
L 0 i 2
E0
Любое комплексное число представимо в виде q = a + ib, а комплексносопряженное как q* = a ib, тогда, с учетом eiωtb= cosωt + i·sinωt, вещественная часть
q(t) равна
q(t ) q (t )
q(t )
qa cos( t ),
2
66.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Вынужденные
электрические
колебания
где qa – амплитуда вынужденных колебаний
qa
E0
L ( ) 4
2
0
2
2
2
2
,
ψ – сдвиг фаз вынужденного колебания
tg
2
.
2
2
0
Подставив значения β и ω0 через параметры колебательного контура, получим
E0
qa
2
,
tg
R
.
1
1
L
R L
C
C
dq
qa sin( t ) qa cos( t )
Теперь найдем силу тока: I
dt
2
I a cos( t ), где Ia = qaω. Запишем последнее выражение в виде
2
I I a cos( t ), где φ = ψ – π/2 – сдвиг по фазе между током и приложенным
2
напряжением
tg tg (
2
)
1
tg
1
C .
R
L
67.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Отсюда следует, что ток отстает по фазе от напряжения
Вынужденные φ > 0, если ωL > 1/ωC и опережает напряжение φ > 0, если ωL < 1/ωC.
электрические
E0
I
q
.
Далее
колебания
a
a
2
1
R L
C
2
С другой стороны, падение напряжений в колебательном контуре запишем в виде
IR
Тогда
q
dI
L
E0 cos t , U R U C U L E0 cos t.
C
dt
U R RI RI a cos( t ) U Ra cos( t ),
U Ra RI a
RE0
1
R 2 L
C
2
.
q qa
U C cos( t ) U Ca cos( t ),
C C
2
qa
E0
Ia
1
U Ca
Ia X C , X C
.
2
C
C
C
1
2
C R L
C
68.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
dI
U
L
I
L
sin(
t
)
I
L
cos(
t
)
U
cos(
t
),
L
a
a
La
Вынужденные
dt
2
2
электрические
U La I a L I a X L ,
колебания
X L L.
Сопоставление формул показывает, что:
напряжение на сопротивлении R изменяется в фазе с током;
напряжение на емкости отстает по фазе от силы тока на π/2;
напряжение на индуктивности опережает по фазе ток на π/2.
Фазовые соотношения можно наглядно представить с помощью фазовой
диаграммы
ULa = ωLIa
1 2
2
2
2
U a U Ra (U La U Ca ) I a R ( L
Ua
C
) Ia Z.
1
L
I a
C
ось токов
URa = RIa
UCa = Ia/ωC
Здесь Z R 2 ( L 1 ) 2
C
- импеданс электрической
цепи.
69.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Необычным и новым в полученных выражениях является
немонотонная зависимость амплитуды колебаний в системе от
частоты вынуждающей силы .
При приближении частоты вынуждающей силы к
резонансной частоте колебаний р амплитуда колебаний начинает
очень сильно возрастать – наступает резонанс.
Резонансная частота для заряда и напряжения на конденсаторе определяется из
выражений: dq 0, dU C 0. d
2
2 2
2 2
2
2
2
4
2
2
4
2 0,
0
0
d
d
d
1
R2
2
2
р 0 2
2.
LC 2 L
При слабом затухании β2 << ω02 резонансная
частота для заряда и напряжения на конденсаторе можно
положить равной ω0, ωрL – 1/ωрС ≈ 0.
Тогда отношение амплитуды напряжения на
конденсаторе к амплитуде внешнего напряжения будет равно
U Cр
Ua
1
1 LC
1 L
Q.
Ua
CR
R
C
R
C
1 2
0
U a 0C R 2 ( 0 L
)
0 C
Вынужденные
электрические
колебания.
Резонанс
70.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Вынужденные
электрические
колебания.
Резонанс
Следовательно, добротность контура Q показывает, во
сколько раз напряжение на конденсаторе при резонансе превышает
приложенное напряжение.
Ток, протекающий в цепи содержащей R, L и С,
Переменный
обусловленный переменным напряжением U = Uacosωt называется
электрический
переменным током.
ток
Амплитуда тока определяется амплитудой напряжения Ua, параметрами
цепи R,L,C и частотой ω.
Ua
Ua
I
.
a
ULa = ωLIa
2
Z
1
R 2 L
C
Ua
φ
URa = RIa
UCa = Ia/ωC
Ток отстает по фазе от напряжения на
I a
угол φ, определяемый из выражения
ось токов
1
L
C .
tg
R
1
L
C
В случае φ < 0, ток опережает напряжение.
71.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Переменный
1 2 - полное электрическое сопротивление или
2
Z R ( L
) импеданс цепи.
электрический
C
ток
Всякая реальная цепь обладает конечными значениями R, L и C. В
отдельных случаях их значения могут быть таковы, что их влиянием на ток можно
пренебречь.
Пусть цепь состоит из одного активного сопротивления R, то есть L = 0, а
C = ∞, закон Ома имеет вид IR = Uacosωt. Отсюда следует, что ток изменяется в
фазе с напряжением, а амплитуда тока равна Ia = Ua/R. R – активное сопротивление.
Пусть R = 0, С = ∞, тогда I a = Ua/ωL = Ua/XL а tgφ = ∞, φ = π/2.
Ток в этом случае отстает от напряжения на π/2. Величину XL = ωL называют
реактивным индуктивным сопротивлением (индуктивным сопротивлением).
Пусть R = 0, L = 0, тогда I a U a U a .
1 / C
XC
XC = 1/ωC – реактивное емкостное сопротивление (емкостное сопротивление).
tgφ = - ∞, φ = - π/2. Ток опережает напряжение на конденсаторе на π/2.
Наконец, пусть R = 0, тогда I a
X L
1
X L XC
C
Ua
L
1
C
Ua
U
a.
X L XC
X
- называется полным реактивным
сопротивлением или реактансом цепи.
tg
X
.
R
72.
КОЛЕБАНИЯ И ВОЛНЫЭлектрические колебания
Переменный Мгновенное значение мощности, выделяемой в цепи равно
электрический
P(t ) U (t ) I (t ) U a cos t I a cos( t ).
ток.
Воспользуемся формулой
Мощность
1
1
cos cos cos( ) cos( ).
2
Тогда P(t )
2
1
1
U a I a cos U a I a cos( 2 t ).
2
2
Практический интерес представляет среднее по времени значение P(t).
Среднее значение c o s (2 t ) 0.
I aU a R
I a2
I aU a
R
R
.
Тогда P P (t )
cos , cos . Подставим cosφ в P: P
2 Z
2
2
Z
I a2
2
Такую же мощность развивает постоянный ток Iд: P RI д R
,
2
Ia
- называется действующим или эффективным значением силы
2 переменного тока.
Тогда средняя мощность переменного тока P = UдIдcosφ.
Входящий в это выражение cosφ – называют коэффициентом мощности.
В технике стремятся увеличить cosφ как можно больше. При малом cosφ для
выделения необходимой мощности нужно пропускать ток большой силы, что
приводит к возрастанию потерь в подводящих проводах.
отсюда I д
73.
ВОЛНЫМеханические волны
Если в каком-нибудь месте упругой (твердой, жидкой или
газообразной) среды возбудить колебания её частиц, то вследствие
взаимодействия между частицами это колебание будет распространяться
от частицы к частице с некоторой скоростью υ.
Процесс распространения колебаний в пространстве называется волной.
Частицы среды, в которой распространяется волна, не вовлекаются волной
в поступательное движение, они лишь совершают колебания возле своего положения
равновесия.
В зависимости от направления колебаний частиц по отношению к
направлению распространения волны, различают продольные и поперечные волны.
Упругие поперечные волны могут возникать лишь в среде, обладающей
сопротивлением к сдвигу.
Поэтому в жидкой и газообразной средах могут возникать только
продольные волны.
В твердой среде возможно возникновение как продольных, так и поперечных
волн.
Распространяясь от источника колебаний, волновой процесс охватывает все
новые части пространства.
Геометрическое место точек, до которых доходят колебания к
моменту времени t, называется фронтом волны.
Упругие
волны
74.
ВОЛНЫМеханические волны
Упругие
волны
Фронт волны представляет собой ту поверхность, которая
отделяет часть пространства, уже вовлеченную в волновой процесс, от
области в которой колебания еще не возникли.
Геометрическое место точек, колеблющихся в
одинаковой фазе, называется волновой поверхностью.
Волновую поверхность можно провести через любую точку пространства,
охваченную волновым процессом.
Следовательно волновых поверхностей существует бесконечное множество,
тогда как волновой фронт в каждый момент времени только один.
Волновые поверхности остаются неподвижными (они проходят через
положение равновесия частиц, колеблющихся в одинаковой фазе).
Фронт волны все время перемещается.
Волновые поверхности могут быть любой формы. В простейших случаях они
имеют форму плоскости или сферы.
Соответствующая волна в этих случаях называется плоской или
сферической.
75.
ВОЛНЫМеханические волны
Пусть плоская волна распространяется вдоль оси х. Тогда
Уравнение
плоской волны все точки среды имеющие одинаковую координату х (но разные y и z)
колеблются в одинаковой фазе.
Здесь ζ – смещение точек среды с различными
ζ
значениями х в некоторый момент времени t.
λ – длина волны, λ = υТ = υ/ν.
х Это не волна, это график функции ζ(x,t) для
некоторого фиксированного момента времени t.
λ
Уравнением волны называется выражение, которое
дает смещение колеблющейся частицы как функцию её
координат и времени ζ(x,y,z,t).
Эта функция должна быть периодичной как относительно координат так и времени.
Периодичность по координате означает, что точки отстоящие друг от друга
на расстояние λ колеблются одинаковым образом.
Периодичность во времени означает, что ζ описывает колебания частиц с
координатами x, y, z.
Найдем вид функции ζ в случае плоской волны, предполагая, что колебания
носят гармонический характер.
Ось х направим по направлению распространения волны, тогда волновые
поверхности будут к оси х, следовательно ζ = ζ(x,t).
76.
ВОЛНЫМеханические волны
Уравнение
плоской волны
ζ
0
Пусть в т. х = 0 ζ (0, t) = Acos(ωt + α). Найдем вид колебаний точек в
плоскости, соответствующей произвольному значению х.
Для того, чтобы волне пройти путь от плоскости х = 0 до
этой плоскости, волне требуется время τ = х/υ (υ – скорость
распространения волны).
Следовательно, колебания частиц, лежащих в
х плоскости х будут отставать по времени на τ от
колебаний частиц в плоскости х = 0.
x = υτ
x
v
( x, t ) A cos( (t ) ) A cos( (t ) ).
Здесь А – амплитуда волны, α – начальная фаза волны, определяется выбором начал
отсчета x и t. Для одной волны обычно α = 0, для многих волн уравнять начальные
фазы нулю не удается.
x
Зафиксируем какое-либо значение фазы (t ) const.
v
Это выражение определяет связь между временем t и тем местом х, в котором фаза
имеет фиксированное значение. Следовательно, вытекающее из этого выражения
dx/dt – дает скорость, с которой перемещается данное значение фазы
Таким образом, скорость распространения волны
dx
dx
dt
0, откуда
v. υ в уравнении волны, есть скорость перемещения
v
dt
фазы, поэтому υ – называют фазовой скоростью.
77.
ВОЛНЫМеханические волны
Так как dx/dt > 0, то волна распространяется в сторону
возрастания х. Уравнение волны, распространяющейся в обратном
x
направлении, имеет вид ( x, t ) A cos( (t ) ), откуда
v
dx/dt = - υ.
Уравнению плоской волны можно придать симметричный вид относительно
х и t, если ввести величину k = 2π/λ – волновое число.
При выводе формулы мы
2
k
, откуда ( x, t ) A cos( t kx ). предполагали, что амплитуда
v
волны А не зависит от х.
Для плоской волы это наблюдается в том случае, когда энергия волны не
поглощается средой. При распространении волны в поглощающей среде –
интенсивность с удалением от источника колебаний постепенно уменьшается –
наблюдается затухание волны.
x
Для затухающих колебаний A A0 e , тогда уравнение плоской волны имеет вид
Уравнение
плоской волны
( x, t ) A0e x cos( t kx ).
Уравнение Всякий источник колебаний имеет некоторую протяженность. Однако
сферической на расстоянии r – значительно превышающем размеры источника r ,
0
волны
источник можно считать точечным.
В изотропной, однородной среде, волна – порождаемая точечным источником
будет сферической, следовательно все точки на волновой поверхности будут
колебаться с одинаковой фазой.
78.
ВОЛНЫМеханические волны
Уравнение Однако амплитуда колебаний в этом случае не остается постоянной,
сферической если даже энергия волны не поглощается средой.
Для непоглощающей среды энергия, излученная источником с его
волны
поверхности остается постоянной.
Тогда N0 = I0S0 = IS. I04πr02 = I4πr2. I ~ A2, I0 ~ A02. A ~ A0/r. Следовательно,
A0
cos( t kx ).
r
Для поглощающей среды A0 e x cos( t kx ).
r
Найдем уравнение волны, распространяющейся в
Уравнение
направлении, образующем с осями координат x, y, z углы α, β, γ.
плоской волны,
распространяющейся Пусть уравнение колебаний, проходящей через начало
координат, имеет вид
в произвольном
cos( t ).
направлении
Возьмем волновую поверхность (плоскость), отстающей от начала координат на
расстояние l
79.
ВОЛНЫМеханические волны
Уравнение
Колебания в этой точке будут отставать от колебаний в
плоской волны,
начале координат на время τ =l/v.
распространяющейся
l
в произвольном
A cos (t ) A cos (t ) A cos t kl .
v
направлении
Выразим l через радиус-вектор r
точек рассматриваемой
поверхности
nr nr cos r cos l.
A cos( t kn r ) A cos( t k r ).
Вектор k kn , равный по модулю 2 / , направленный по
нормали к волновой поверхности и определяющий
направление распространения и пространственный период
плоской монохроматической волны, называется волновым
вектором.
В направлении волнового
вектора происходит наибыстрейшее изменение
фазы волны. Для перехода
от r к x, y, z выразим
A cos( t k r ) A cos( t k x x k y y k z z ).
Где
kx
2
cos , k y
2
cos , k z
2
cos .
80.
ВОЛНЫМеханические волны
Уравнение
любой
волны
является
решением
дифференциального уравнения , называемого волновым.
Чтобы установить вид волнового уравнения, сопоставим вторые
частные производные по координатам и времени от функции ζ(x, y, z), описывающей
плоскую волну
2
2
A cos( t k r ) 2 .
2
Волновое
уравнение
t
2
2
k x A cos( t k r ) k x2 .
2
x
2
2
2
k
A
cos(
t
k
r
)
k
.
y
y
2
y
2
2
2
k
A
cos(
t
k
r
)
k
.
z
z
2
z
Сложение производных по координатам дает
1
2 2 2
2
2
2
2
,
(
k
k
k
)
k
.
2
x
y
z
2
2
2
k
x
y
z
1 2
2 2 ,
t
k 2 2
2 2 .
t
2
2
2 -оператор
где 2 2 2 Лапласа.
x y
z
Волновому уравнению удовлетворяет
1 2
2 2 . любая функция, имеющая аргумент
v t
f ( x, y, z , t ) f ( t k r ).
81.
ВОЛНЫМеханические волны
Пусть в направлении оси х распространяется
Скорость упругих
продольная плоская волна.
волн в твердой среде
Выделим в среде цилиндрический объем с площадью
х
х + Δх
основания S и высотой Δх.
Если основание цилиндра с координатой х имеет
смещение ζ, то смещение с координатой х + Δх равно
Δх
ζ + Δζ. Рассматриваемый
объем
х деформируется, он получает удлинение
Δζ > 0 или сжатие, если Δζ < 0.
σ (х+ζ)
σ (х+Δх+ζ+ Δζ)
Относительное удлинение Δζ / Δx дает
среднюю деформацию цилиндра, так как ζ меняется
с изменением х не по линейному закону, то истинная
деформация в разных сечениях цилиндра будет
неодинаковой.
ζ
ζ+ Δζ
.
Чтобы получить деформацию в сечении х надо Δх→0, тогда
x
Наличие
деформации
растяжения
(сжатия)
свидетельствует
о
существовании
нормального
напряжения
σ,
при
малых
деформациях
пропорционального величине деформации
E E
, где Е – модуль Юнга.
x
82.
ВОЛНЫМеханические волны
Скорость упругих
волн в твердой среде
ζ
Относительная деформация, а следовательно и σ зависит от х.
0, 0.
x
0, 0.
x
х
0, 0.
x
0, 0.
x
Следовательно положительные и отрицательные деформации чередуются
друг с другом (растяжение и сжатие).
Поэтому продольная волна состоит из чередующихся разрежений и
сгущений среды.
83.
ВОЛНЫМеханические волны
Запишем теперь для нашего цилиндрического объема
Скорость упругих уравнение движения.
волн в твердой среде Полагая Δх очень малым будем считать, что проекция
ускорения на ось х будет одинаковой для всех точек цилиндра и равной
2
a
t 2
.
Масса цилиндра равна m S x, где ρ – плотность недеформируемой среды.
Проекция силы на ось х
Fx S SE
.
x x x
Значение производной
точностью
x x
в сечении х + δ, где δ << 1 можно считать с большой
x
2
2 .
x x x x x
2
2
В виду малости Δх, ζ и Δζ Fx SE
(
x
)
2
2
x
x
x
x
x
x
2
2
SE
(
x
)
SE
x
,
1.
2
2
x
x
x
84.
ВОЛНЫМеханические волны
Скорость упругих
волн в твердой среде
2
2
Fx max . SE
x S
x.
2
2
x
t
2
2
1
E
.
.
v
.
2
2
2
x
E t
E
v
Фазовая скорость продольных упругих волн зависит от модуля Юнга и
плотности среды.
G
Для поперечных волн v
, где G – модуль сдвига.
85.
ВОЛНЫМеханические волны
Энергия
упругой
волны
Пусть в некоторой среде распространяется в направлении оси х
плоская продольная волна
( x, t ) A cos( t kx ).
Выделим в среде элементарный объем ΔV настолько малым, чтобы
производные / t , / x были одинаковыми во всех точках этого объема.
2
mv 2
Выделенный объем обладает
K
V .
кинетической энергией
2
2 t
2
2
Потенциальная энергия
E 2 E
v 2
2
П
V
V
,
E
v
.
упругой деформации равна
2
2 x
2 x
2
2
1
2
W K П
Полная энергия
v
V .
2 t
x
2
2
W
1
2
Объемная плотность
w
v
.
V
2
t
x
энергии
Найдем производные
A sin( t kx ),
t
kAsin( t kx ).
x
86.
ВОЛНЫМеханические волны
Энергия
упругой
волны
Тогда
w
1
2 A2 v 2 k 2 A2 sin 2 ( t kx ), так как v 2 k 2 2 ,
2
то
w 2 A2 sin 2 ( t kx ).
Из этой формулы следует, что мгновенные значения плотности энергии в
каждый момент времени в разных точках пространства различны.
Найдем среднее значение плотности энергии
1
w A sin ( t kx ) 2 A2 .
2
2
2
2
Подобная
зависимость
имеет
место
для
всех
видов
волн,
распространяющихся в непоглощающих и поглощающих средах.
Итак, среда, в которой распространяется волна, обладает дополнительным
запасом энергии. Эта энергия доставляется от источника колебаний в различные
точки среды самой волной.
Следовательно, волна переносит с собой энергию.
87.
ВОЛНЫМеханические волны
Поток
энергии
Количество энергии, переносимой волной через некоторую
поверхность в единицу времени, называется потоком энергии через эту
поверхность
dW
Φ
dt
.
Поток энергии в разных точках среды может обладать
Плотность
различной интенсивностью. Поэтому вводится векторная (локальная)
потока
энергии. величина, называемая плотностью потока энергии (вектором Умова).
Эта величина численно равна потоку энергии через единичную
Вектор
площадку, помещенную в данную точку среды перпендикулярно к
Умова
направлению, в котором переносится энергия волны.
Направление вектора плотности энергии совпадает с направлением переноса энергии
Φ
W
S
j
.
S S t
v
vΔt
W w S v t.
Тогда
j wv
j wv,
или
- вектор Умова.
88.
ВОЛНЫМеханические волны
Интенсивность
волны
Вектор
Умова меняется со временем по величине
2 2 2
j v ρω A sin ( t kx ).
Найдем среднее по времени значение плотности потока энергии (вектора Умова)
1
2 2
j w v A v .
2
Эта формула, справедливая для всех видов волн, определяет интенсивность волны,
то есть энергию, переносимую волной через единичную площадку в единицу времени.
С другой стороны, поток энергии через элементарную площадку равен
Через поверхность S
dФ j dS .
Ф j dS .
S
Через замкнутую поверхность S
Ф j dS .
S
Аналогично для средних
значений потока, например
Ф j dS .
S
89.
ВОЛНЫМеханические волны
Если в среде распространяются одновременно несколько волн, то
колебания частиц среды оказываются геометрической суммой
колебаний, которые совершали бы частицы при распространении
каждой из волн в отдельности.
Следовательно волны просто накладываются одна на другую, не возмущая
друг друга.
Это, вытекающее из опыта утверждение, называется принципом
суперпозиции (наложения ) волн.
При наложении большого количества волн с разной частотой от
суммирования переходят к интегрированию. Этот интеграл называется интегралом
Фурье.
Наибольший интерес представляет наложение когерентных волн, в
результате сложения которых возникает явление интерференции.
Частный, но очень важный случай интерференции наблюдается при
наложении двух встречных плоских волн с одинаковой частотой и амплитудой.
Запишем уравнения этих волн, распространяющихся вдоль оси х в
противоположных направлениях
Стоячие
волны
1 A cos( t kx 1 ),
2 A cos( t kx 2 ).
90.
ВОЛНЫМеханические волны
Стоячие
волны
В результате сложения этих волн
1 2 2 A cos
2 1
2
cos
2 1
2
2 1
2 1 -мы получили уравнение
2 A cos kx
cos t
стоячей волны.
2
2
Упростим это выражение: выберем начало отсчета х так, чтобы α2 - α1 = 0, а
начало отсчета t – так, чтобы α2 + α1 = 0.
2 A cos kx cos t 2 A cos 2
x
cos t.
Из уравнения следует, что колебания происходят с той же частотой, что и у
встречных волн, а амплитуда зависит от х
A( x) 2 A cos 2
Если
cos 2
x
1,
x
.
то A(x) =2A = max.
Эти точки называются пучностями стоячей волны.
91.
ВОЛНЫМеханические волны
Координаты
пучностей
Получим значение координат пучностей из условия, что cosnπ = ±1,
тогда
x
2
п
n , n 0,1, 2, ....
xп n .
2
Следует иметь ввиду, что эта координата не одной точки плоской волны, а плоскости,
точки которой имеют координату определяемую формулой для хп.
Если cos(2πx/λ) = 0, то эти точки называются узлами стоячей волны.
Координаты
узлов
Координаты узлов стоячей волны определим из условия
2
xу
1
(n ) ,
2
1
x у (n ) .
2 2
Следует также иметь ввиду, что узел не точка, а плоскость.
Расстояние
между соседними
пучностями
xп xп (n 1) xп (n) (n 1) n .
2
2 2
Расстояние
между соседними
узлами
1
1
x у x у (n 1) x у (n) (n 1) (n ) .
2
2
2 2 2
92.
ВОЛНЫМеханические волны
Расстояние между
узлом и пучностью
1
x уп х у (n) xп (n) (n ) n .
2 2
2 4
Из уравнения стоячей волны, координат пучностей и узлов, а также
расстояний между ними следует, что по разные стороны от узла частицы среды
колеблются в противофазе, а все частицы среды, заключенные между соседними
узлами колеблются в фазе (синфазно).
Рассмотрим поведение скорости и относительной деформации частиц среды
x
2 A cos 2 sin t ,
t
2
x
2
A sin 2 cos t.
x
Представим графически поведение смещения, скорости и относительной
деформации частиц среды в два момента времени.
93.
ВОЛНЫМеханические волны
ζ
Стоячие
0
волны
х
ζ
0
х
0
х
ζ
0
х
0
х
0
х
ζ
Из графиков видно, что
узлы и пучности скорости
совпадают с узлами пучностями
смещения ζ.
t=0
Узлы
и
пучности
деформации
ε
совпадают
с
пучностями и узлам смещения ζ.
В то время, когда ε = max 0
и наоборот. Соответственно,
дважды за период происходит
превращение энергии стоячей
волны то полностью в
t = T/4 потенциальную вблизи
узлов волны (или пучностей
деформации), то полностью в
кинетическую в пучностях волны
(пучностях скорости).
94.
ВОЛНЫМеханические волны
Стоячие
волны
В результате происходит переход энергии волны от каждого
узла к соседним пучностям и наоборот.
Отсюда следует, что средний поток энергии в любом сечении волны равен нулю.
Это свойство стоячей волны играет очень важную, можно сказать
фундаментальную роль в Природе.
Стоячая волна является квазистационарной в том смысле, что она
неподвижна (в отличии от бегущей волны) и сосредоточена (локальна) в той области
пространства, где эта волна находится.
Если система, в которой возбуждена эта волна, не взаимодействует с
окружающей средой, то энергия этой волны может оставаться постоянной (система не
излучает энергию в окружающее ее пространство).
Взаимодействие с окружающей средой может перевести систему с другим
состоянием стоячей волны. Поясним это на примере.
В закрепленной с обеих концов натянутой струне при возбуждении
Колебания
поперечных колебаний возникают стоячие волны, причем в местах
струны
крепления струны всегда располагаются узлы.
Поэтому с заметной интенсивностью возбуждаются в струне такие колебания,
половина длины волны которых укладывается на длине струны целое число раз.
95.
ВОЛНЫМеханические волны
Колебания
струны
ℓ
1
1
2
2
2
2
m
Обобщаем - n
n
, n 1, 2, 3, ... .
2
v
v
n.
Тогда n
n 2
Здесь v f ( Fн , ) - фазовая скорость волны, зависящая от силы натяжения
струны Fн и значения массы струны на единицу ее длины m/ℓ (см. Тюрин Ю.И.
«Электродинамика»).
А теперь перейдем к частоте n- это собственные частоты колебаний
(гармоники) струны.
Частота 1 (при n = 1) называется основной частотой или основным тоном.
Частоты с n > 1называются высшими тонами или обертонами.
Таким образом, колебания струны замечательны тем, что для них по
классическим представлениям получаются дискретные значения частоты.
Для классической физики это исключение.
Для квантовой физики это правило, чем исключение.
Посмотрим, качественно, как это получается.
96.
ВОЛНЫМеханические волны
Колебания Обратите внимание на второй рисунок, где в центре струны постоянно
струны
существует узел, а струна в этом месте не закреплена.
Что произойдет, если линейную струну превратить в кольцо? Конечно возбудить
стоячие волны в такой струне достаточно сложно, поэтому возьмем жесткое кольцо.
Стукните колечко и оно зазвучит, возникает линейная стоячая волна,
замкнутая сама на себя.
Постройте на этом кольце полусферу – колокол (о звучании я уже не говорю),
можно дополнить систему до полной сферы, звучание вне которой достаточно слабое
(интересно послушать, что там внутри?). Возникает объемная стоячая волна.
Таким образом, возможно возникновение замкнутых самих на себя
(пространственно ограниченных) линейных, плоских (бубен) и объемных стоячих
волн.
А теперь перейдем от исключения в макроскопическом мире - к правилу в
микромире.
Из уравнений Максвелла следует, что при движении свободного заряда
(например, электрона) с ускорением этот заряд теряет энергию в виде
электромагнитных волн.
Электроны в атоме (микромир ~ 0,1 нм), казалось бы, двигаясь по
замкнутым траекториям и, следовательно, с ускорением - должны излучать энергию,
что приводит к невозможности существования атомов.
97.
ВОЛНЫКолебания
Электроны в атоме, находясь в связанном состоянии из-за
струны
взаимодействия с ядром атома и остальными электронами, создают
свои собственные объемные «коконы» стоячих волн де Бройля (корпускулярноволновой дуализм).
Такая электронная система атома находится в квазистационарном
состоянии, поэтому не излучает и проявляет себя только при внешнем воздействии.
Электрон, поглотив извне фотон с определенной порцией энергии (кратной
n), создает новый «кокон» стоячей волны, а затем, испустив фотон, может вернуться в
свой прежний «кокон».
Если упругие волны, распространяющиеся в воздухе, имеют
Звуковые
частоту от 16 до 20000 Гц, то достигнув человеческого уха, они вызывают
волны
ощущение звука.
В соответствии с этим упругие волны в любой среде, имеющие частоту в
указанном диапазоне, называются звуковыми волнами или просто звуком.
Вне этого диапазона, при ν < 16 Гц – называют инфразвуком, при ν > 20000 Гц
– ультразвуком.
Воспринимаемые звуки люди различают их по высоте, тембру и громкости.
Каждой из этих субъективных характеристик соответствует определенная
объективная физическая характеристика звуковой волны.
Всякий реальный звук представляет собой наложение гармонических
колебаний с определенным набором частот.
98.
ВОЛНЫНабор частот колебаний, присутствующих в данном звуке,
Звуковые
называют его акустическим спектром.
волны
Если в звуке присутствуют колебания всех частот от ν1 до ν2, то спектр
называется сплошным. Сплошным акустическим спектром обладают шумы.
Если звук состоит из колебаний дискретных частот ν1, ν2, …, νi, …, νn, то
спектр называют линейчатым.
Колебания с линейчатым спектром вызывают ощущения звука, с более или
менее определенной частотой. Такой звук называется тональным.
Высота тонального звука определяется основной (наименьшей) частотой.
Набор колебаний с более высокими частотами называется обертонами. Их
относительная интенсивность определяет окраску или тембр звука.
Под интенсивностью звука понимают среднее значение по времени
плотности потока энергии, которую несет с собой звуковая волна.
Для того, чтобы вызвать звуковое ощущение, звуковая волна должна
обладать некоторой минимальной интенсивностью, которая называется порогом
слышимости.
Порог слышимости различен для разных людей и сильно зависит от частоты
звука.
Наиболее чувствительно человеческое ухо к частотам от 1000 до 4000 Гц. В
этой области частот порог слышимости составляет в среднем ~ 10-12 Вт/м2.
99.
ВОЛНЫПри интенсивности ~ 1 ÷ 10 Вт/м2 волна перестает восприниматься
как звук, вызывая лишь давление и болевое ощущение в ушах.
Значение интенсивности, при котором это
болевого L, дБ
происходит называется порогом болевого
j, Вт/м2 Порог
ощущения
ощущения.
Субъективно оцениваемая громкость
1
120
звука возрастает гораздо медленнее, чем
интенсивность звуковой волны.
При возрастании интенсивности в
10-4
80
геометрической
прогрессии
громкость
возрастает приблизительно в арифметической,
Порог
-8
10
40
то есть линейно.
слышимости
На
этом
основании
уровень
громкости определяется как логарифм
10-12
0
отношения интенсивности данного звука I к
20
200
2000 20000 ν, Гц интенсивности I0, принятой за исходную
Единица уровня громкости, определяемая L lg I .
I0
этой формулой называется белом (Б).
I
Обычно пользуются в 10 раз большими
L 10 lg
.
I0
единицами – децибелами (дБ)
Исходная интенсивность I0 ≈ 10-12 Вт/м2, так что порог слышимости при
частоте ~ 1000 Гц лежит на нулевом уровне (L = 0).
Звуковые
волны
100.
ВОЛНЫЗвуковая
волна
в
газах
представляет
собой
распространяющуюся
в
пространстве
последовательность
чередующихся областей сжатия и разрежения газа.
Следовательно, давление в каждой точке пространства испытывает
периодически изменяющееся отклонение ΔР от среднего значения Р в данной точке
пространства в отсутствии волны P P P.
Пусть плоская волна распространяется вдоль оси х. Выделим в среде
цилиндр площадью S и высотой Δх.
х
х + Δх
Запишем уравнение движения F = ma .
Скорость звука
в газах
x
Δх
Р’ (х+ζ)
x
Масса газа, заключенная в этом объеме, равна
m = ρSΔx, где ρ – плотность невозмущенной среды.
Полагая Δх очень малым будем считать,
х что проекция ускорения на ось х будет
одинаковой для всех точек цилиндра и
2
равной
P’(х+Δх+ζ+ Δζ)
a
t 2
.
Проекция силы на ось х
Fx S P( x x ) P( x ) .
ζ
ζ+ Δζ
В виду малости Δх, ζ и Δζ значение P’ в сечении (х+
δ), где δ << 1 можно считать с большой точностью
P
P( x ) P( x )
.
x
101.
ВОЛНЫP
P
( x ) Px
Скорость звука Тогда Fx S Px
x
x
в газах
P
P
S
( x )
S x,
1.
x
x
x
2
P
S
x
S x.
С учетом уравнения движения запишем
2
t
x
2
P
Теперь найдем связь между Р’ и ζ.
.
Тогда
2
t
x
Эта связь зависит от характера процесса сжатия
(или расширения) газа.
В звуковой волне сжатие и расширение происходят так часто, что смежные
участки среды не успевают обмениваться теплом, поэтому эти процессы можно
считать адиабатическими PV const , cP / cV .
Тогда, для нашего цилиндра
P ( S x ) P S ( x ) P S ( x
x ) P ( S x ) 1
.
P P 1
.
x
x
1,
x
P P 1
P P 1
.
x
x
Так как
x
то после разложения в ряд получим
1
Продифференцируем
P 1
. последнее выражение по
x
∂х.
102.
ВОЛНЫСкорость звука
в газах
P
2
P
.
x
x 2
2
2
2 P 2 .
t
x
Подставим это выражение в
2
2
.
2
2
x
P t
Мы получили волновое уравнение где
1
.
2
v
P
Окончательно, фазовая скорость звука в газе
(при адиабатическом распространении волны) равна
Если сравнить скорость волны
в газе с ее скоростью в твердых телах
v
E
v
,
P
.
v
G
,
то видно, что в числителе дроби стоит модуль соответствующей упругой деформации.
Рассмотрим это подробнее. Тело называется упругим, а его деформации,
вызываемые внешними воздействиями, называются упругими деформациями, если
они полностью исчезают после прекращения этих воздействий. При достаточно
малых деформациях все тела практически можно считать упругими.
Упругие свойства тел зависят от характера теплового движения молекул и
сил их взаимодействия.
Упругость твердого тела обусловлена силами взаимного притяжения и
отталкивания частиц (ионов, атомов или молекул), образующих это тело и
совершающих беспорядочные тепловые колебания около узлов его кристаллической
решетки.
103.
ВОЛНЫСкорость звука Силы взаимодействия частиц препятствуют деформациям
кристаллической решетки, связанным с изменением как объема
в газах
тела, так и его формы. Поэтому твердые тела помимо объемной упругости обладают
упругостью формы, которая проявляется в сопротивлении деформации сдвига.
Следовательно, в твердых телах могут распространяться как продольные,
так и поперечные волны.
Газообразное тело беспрепятственно изменяет свою форму в соответствии с
формой занимаемого им сосуда – газ не обладает упругостью формы.
В то же время газу присуща объемная упругость, то есть сопротивляться изменению
его объема вследствие теплового движения молекул.
Следовательно, в газах не возникают деформации сдвига и, поэтому, в этой
среде распространяются только продольные волны.
Жидкое тело занимает, по своим физическим свойствам, промежуточное
положение между твердыми и газообразными телами.
Из-за очень малой средней продолжительности τ оседлого существования
молекул жидкости она, подобно газам, обладает только объемной упругостью.
Поэтому в объеме жидкости могут распространяться только продольные волны.
Однако поверхность жидкости (толщиной 1~2 радиуса молекулярного
действия) обладает физическими свойствами, отличающимися от свойств объема.
В этом слое определяющую роль играют силы поверхностного натяжения,
которые наряду с силами тяготения приводят к распространению поверхностных
волн, возникающих под влиянием внешних воздействий (падения тел, ветра и т.д.).
104.
ВОЛНЫВ поверхностных волнах частицы жидкости одновременно
Скорость звука
совершают поперечные (упругость формы поверхности) и
в газах
продольные
колебания,
сложение
которых
приводит
к
эллиптическим или более сложным траекториям.
Окончательно, скорость звука в газах равна
где К – модуль объемной упругости газа, зависящий от
P
K термодинамического процесса. При очень медленном
v
, изменении объема газа процесс можно считать
изотермическим, а при очень быстром –
адиабатическим.
В первом случае К = Р, а во втором К = γР.
Оценим скорость распространения звуковой волны в газах.
При атмосферном давлении и обычных температурах большинство газов близки по
своим свойствам к идеальному газу, тогда
PV
m
RT , P
RT ,
P
RT
,
v
RT
.
Сравним скорость волны со средней скоростью движения молекул газа
v мол
Отсюда, скорость волны в газе немногим
v
,
1. меньше средней скорости хаотического
v мол
8
8RT
движения молекул этого газа.
105.
ВОЛНЫЭффект Доплера
Пусть в газе или жидкости находятся источник и
для звуковых волн приемник звуковых волн.
Если источник и приемник неподвижны относительно среды в которой
распространяется волна, то принимаемая частота колебаний приемником будет
равна частоте колебаний источника ν0.
Если же источник или приемник, либо оба, движутся относительно среды, то
частота колебаний, воспринимаемая приемником ν, может отличаться от частоты
источника ν0. Это явление называется эффектом Доплера.
Предположим, что источник и приемник движутся вдоль соединяющей их
прямой.
Скорость источника vист будем считать положительной, если источник
движется к приемнику, и отрицательной, если источник движется от приемника.
Аналогично, скорость приемника vпр положительна, если приемник
движется к источнику, и отрицательной, если приемник движется от источника.
106.
Электромагнитные волныУравнения
Максвелла
Закон
Гаусса
Интегр. форма
Диффер.
форма
Эл. поле
DdS dV
Маг. поле
B
dS 0
S
div D
V
divB 0
S
Полного тока
D
L H dl S j t dS
Электромагнитной
индукции
B
L Edl - S t dS
Соотношения
D 0 E,
D
rotH j
t
B 0 H,
B
rotE t
j σE jстор
Существование электромагнитных волн вытекает из уравнений Максвелла.
B
E
,
t
D
H j
,
t
B 0.
D .
0
Рассмотрим случай однородной, нейтральной (ρ = 0), непроводящей среды
(j = 0) с постоянными ε и μ, тогда, с учетом соотношений, получим
107.
Электромагнитные волныH
E 0
H 0
1
2
t
E
E 0
H 0
3
4
t
Возьмем ротор от обеих частей уравнения 1
H
E 0
H .
0
t
t
2
E
Перепишем полученное уравнение с учетом 3
E 0 0
.
2
t
Теперь преобразуем левую часть полученного
используя
выражения,
правило двойного векторного произведения a b c b ( a c ) c ( a b ).
E ( E ) ( ) E E. Здесь ( E ) 0 , согласно 4 .
2
E
1
.
Следовательно E 0 0
Так
как
, окончательно получим
0 0
2
t 2
c
E
E 2
.
2
c t
2
5
108.
Электромагнитные волныТеперь возьмем ротор от уравнения
3
2
E
H
0
E
.
0
0
0
2
t
t
t
Левая часть полученного выражения равна H H .
H
H
H 2
.
2
c
t
2
Окончательно
6
6 неразрывно связаны друг с другом и представляют собой
Уравнения 5
типичные волновые уравнения.
Всякая функция, удовлетворяющая этим уравнениям, описывает некоторую
волну, фазовая скорость которой равна
c
v
.
В вакууме ε = μ = 1, следовательно
v c.
109.
Электромагнитные волныНайдем решение уравнений 0
в общем виде, а затем перейдем к
упрощениям. Начнем с уравнения для электромагнитной индукции.
i
j k
E z E y E x E z E y E x
j
E
i
k
x y z
z
x
y
z
y
x
B
By
Ex E y Ez
Bx
z
i
t
j
t
k
.
t
Теперь от векторных уравнений
Bx By Bz
Уравнение Гаусса B
0 перейдем системе уравнений в
x
y
z
скалярной форме.
E z
y
E x
z
E
y
x
Bx
x
E y
z
E z
x
E x
y
B y
Bz
y
z
0
Bx
t
B y
t
Bz
t
H z
y
H x
z
H
y
x
Dx
x
H y
z
jx
Dx
t
D y
H z
jy
x
t
H x
Dz
jz
y
t
D y
Dz
y
z
110.
Электромагнитные волныТеперь перейдем к упрощениям.
Опять рассмотрим случай однородной, нейтральной (ρ = 0), непроводящей
среды (j = 0) с постоянными ε и μ.
Направим ось х перпендикулярно волновым поверхностям. Тогда векторы Е
и Н и их компоненты по координатным осям не будут зависеть от y и z.
Тогда частные производные от всех компонент векторов Е и H по
координатам у и z будут равны нулю и уравнения упростятся следующим образом (с
учетом соотношений)
H x
0
0
♥
t
H
y
E z
0
x
t
E
H
y
z
0
x
t
B
H
x
x
0
0
♥
x
x
E x
0
0
♥♥
t
E
y
H z
0
x
t
H
E
y
z
0
x
t
D
E
x
x
0
0 ♥♥
x
x
Уравнения (♥) и (♥♥) показывают, что Нх и Ех не зависят от х и t.
Следовательно, отличные от нуля Нх и Ех могут быть обусловлены постоянными,
однородными магнитными и электрическими полями, накладывающиеся на
электромагнитное поле волны. В дальнейшем будем считать, что Нх = Ех = 0.
111.
Электромагнитные волныОтсюда следует очень важный вывод, что само поле электромагнитной
волны не имеет составляющей вдоль оси х.
Отсюда вытекает, что векторы Е и Н перпендикулярны направлению
распространения волны, то есть электромагнитные волны – поперечны.
Оставшиеся уравнения объединим в две независимые группы.
E y
H
0 z ,
x
t
E y
H z
0
.
x
t
H y
Ez
0
,
x
t
H y
x
0
Ez
.
t
7
8
Первая группа уравнений связывает компоненты Еу и Нz – вторая Еz и Ну.
Для описания плоской электромагнитной волны достаточно взять одну систему
уравнений. Положим Еz = Ну = 0. 2
2
2
7
продифференцируем по х.
Аналогично
Ey
x 2
E y E y
H z
0
0 0
2
.
2
2
t x
t
c t
2 H z 2 H z
2
.
2
2
x
c t
112.
Электромагнитные волныОдним из возможных решений полученной системы волновых уравнений,
относительно Еу и Нz, является синусоидальная гармоническая электромагнитная
волна, распространяющаяся от источника в положительном направлении оси х:
Eу = E0cos( t – kx + 1),
Hz = H0cos( t – kx + 2),
где частота; k волновое число; 1, 2 начальные фазы колебаний; Е0, Н0
амплитуды колебаний.
Подставляя решения в исходную систему уравнений, 7
получаем
kE0sin( t – kx + 1) = 0 H0sin( t – kx + 2),
kH0sin( t – kx + 2) = 0 E0sin( t – kx + 1).
Для того чтобы эта система удовлетворялась, необходимо равенство фаз 1 =
2 и выполнение соотношений
kE0 = 0 H0,
0 E0 = kH0.
Отсюда следует соотношение между амплитудными значениями Е0 и Н0 и,
аналогичное ему между мгновенными значениями Е и Н.
0 E0 0 H 0 ,
0 E 0 H .
113.
Электромагнитные волныТаким образом, в электромагнитной волне колебания электрического и
магнитного полей происходят с одинаковой фазой ( 1 = 2) и между амплитудами
колебаний в вакууме (μ = 1, ε = 1) выполняется соотношение (в СИ)
E0
H0
0
12,566 10 7
377 Ом.
12
0
8,854 10
114.
Электромагнитные волныЭлектромагнитная волна переносит энергию, плотность потока которой
определяется вектором Умова – Пойнтинга
S EH
(Вт/м2).
Вектор S может быть записан через удельную плотность энергии w:
где
0 E 2 0 H 2
w
2
S wv ,
(Дж/м3).
Поскольку энергия и масса связаны
соотношением Эйнштейна E = mс2, то электромагнитное поле обладает массой с
плотностью m/V = w/с2 и импульсом с плотностью:
P
w
g
2 v.
V
c
Импульс электромагнитных волн проявляется, в частности, в световом
давлении
S
p gc(1 r ) (1 r ) w(1 r ) (Па).
c
Здесь r коэффициент отражения, который можно определить как отношение
квадратов амплитуд напряженностей электрического поля в отраженной Е0 и
падающей Е0 волнах: r = (Е0 /Е0)2 или как отношение потока излучения, отражённого
телом, к упавшему на него потоку излучения.
115.
Электромагнитные волны116.
Электромагнитные волныСветовая волна
Абсолютный
показатель
преломления
Оптическую плотность среды, при прохождении в ней
электромагнитной волны, характеризует абсолютный показатель
преломления n, определяемый из фазовой скорости волны
c
n
v
.
Для подавляющего большинства прозрачных веществ μ ~ 1, поэтому
n .
Для воды значение ε, полученное из электростатических измерений, равно
81, однако n = 1,33. Отсюда следует, что в быстропеременных электрических полях ε
– становится иным, и зависит от частоты колебаний n = n(ν), в этом заключается
явление дисперсии света.
Длины волн видимого света лежат в пределах λ = (0,4 ÷ 0,78) мкм. Эти
значения относятся к вакууму, в веществе длины световых волн будут иными.
При переходе света из вакуума в
среду его частота не изменяется ν0 = ν. Тогда
c
0
v
,
0
v
0.
c
n
Длина световой волны в среде
уменьшается в n раз по отношению к вакууму.
117.
Электромагнитные волныСветовая волна
Частота изменения вектора плотности потока энергии, переносимой волной, ~ 2ν.
Поэтому ни глаз, ни какой-либо прибор не может уследить за столь частыми
изменениями потока энергии. Следовательно они регистрируют усредненный по
времени поток.
Модуль среднего по времени значения плотности потока энергии,
переносимой волной, носит название интенсивности света I в данной точке
пространства.
I S EH .
Интенсивность света пропорциональна квадрату амплитуды волны, поэтому
E0 0 H 0
0
E0 , ~ 1, H 0 ~ nE0 .
0 . H 0
0
I ~ H 0 E0.
В оптических явлениях основную роль играет электрическое поле, поэтому
вектор Е называется – световым вектором. Влияние магнитного поля в с раз меньше.
Следовательно
I ~ nE02 .
Световой
Линия, вдоль которой распространяется световая энергия, называется
луч
световым лучом.
Усредненный вектор Умова-Пойтинга направлен в каждой точке
пространства по касательной к лучу.
118.
Электромагнитные волныСветовая волна
В изотропных средах направление
S совпадает с нормалью к волновой
поверхности, то есть с направлением k - волнового вектора.
Отсюда следует, что в изотропных средах лучи перпендикулярны волновым
поверхностям.
В анизотропных
средах нормаль к волновой поверхности в общем случае не
совпадает с S , в этом случае лучи не ортогональны к волновым поверхностям.
119.
Электромагнитные волныОтражение и преломление
плоской волны на границе двух диэлектриков
Пусть плоская электромагнитная волна падает на плоскую границу раздела
двух однородных и изотропных диэлектриков.
Диэлектрик, в котором распространяется
падающая волна – характеризуется ε1, второй
α'
– проницаемостью ε2.
α
Определим направление распространения
k
k
помощью
волнового
падающей волны с
ε1
вектора k , отраженной волны с
помощью
х
τ
вектора k и преломленной - k
ε2
n
у
β
k
Наша задача – найти связь между k' и k'' с k.
Для этого выберем систему координат и введем
единичные орты τ и n.
Далее воспользуемся тем, что на границе раздела двух
диэлектриков тангенциальные составляющие напряженности электрического поля
волны в первой и второй среде равны Е1τ = Е2τ.
Плоскость, в которой лежат векторы k и n назовем плоскостью падения волны.
120.
Электромагнитные волныОтражение и преломление
плоской волны на границе двух диэлектриков
Колебания вектора E падающей
волны
запишем
экспоненциальной функции
i ( t k x x k y y )
i ( t k r )
E E0e
E0e
с
помощью
, при z 0.
Так же определим напряженность поля в отраженной и преломленной волнах
i ( t k r ) i ( t k x x k y y 1 )
1
E E0 e
E0 e
,
i ( t k r ) i ( t k x x k y y 2 )
2
E E0 e
E0 e
.
Результирующее поле в первой среде равно
i ( t k x x k y y )
i ( t k x x k y y 1 )
1
0
0
Результирующее поле во второй среде равно
i ( t k x x k y y 2 )
2
0
Согласно равенству тангенциальных составляющих на границе раздела двух
сред (у = 0) получим
i ( t k x )
i ( t k x )
i ( t k x )
E E E E e
E e
E E e
.
x
x
1
E0 e
E0 e
E0 e
.
x
2
.
121.
Электромагнитные волныОтражение и преломление
плоской волны на границе двух диэлектриков
Для того, чтобы это равенство выполнялось при любом t, необходимо
равенство всех частот
Отсюда вывод: частоты отраженной и преломленной волн совпадают с
частотой падающей волны.
Для того, чтобы это равенство выполнялось при любом х, необходимо
равенство
x
x
x
Из рисунка следует, что
k k k .
k x k sin ,
k x k sin ,
k x k sin .
v1
k sin k sin k sin .
k
sin
v1
v1
,
k
sin
v2
v1
,
k
sin .
Отсюда следует, что - закон отражения:
Угол падения равен углу отражения и лучи падающий и
отраженный лежат в плоскости падения.
v2
.
122.
Электромагнитные волныОтражение и преломление
плоской волны на границе двух диэлектриков
Далее следует
sin
v
c v1 n2
1
n21 - закон преломления:
sin v2 v2 c
n1
Отношение синуса угла падения к синусу угла преломления
равно относительному коэффициенту преломления. Лучи
падающий и преломленный лежат в плоскости падения.
При преломлении света возможны 2 случая:
sin
n
1. Пусть n2 > n1, тогда
2 1, .
sin
n1
sin
n
2. Пусть n2 < n1, тогда
2 1, .
sin
n1
αпр
α
β
β = π/2
α
β
sin пр
n2
.
n1
При α > αпр возникает явление
полного внутреннего отражения.
123.
Электромагнитные волныОтражение и преломление
плоской волны на границе двух диэлектриков
Соотношения
между амплитудами
и фазами
падающей,
отраженной и
преломленной волн.
Для простоты ограничимся случаем нормального
падения волны на поверхность раздела диэлектриков.
Пусть колебания вектора Е совпадает с осью х, тогда орт τ
совпадет с ортом i.
Тогда уравнение непрерывности тангенциальной
составляющей примет вид
Ex Ex Ex .
1
Для мгновенных значений Н ~ nE, тогда, вследствие закона сохранения энергии,
I x I x I x .
n1 E 2 x n1 E x 2 n2 E x 2 .
Из 1
2
найдем Ex Ex Ex и подставим в 2
n1Ex2 n1 Ex Ex n2 Ex 2 .
n1 E x2 n1 E x 2 2n1 E x E x n1 E x2 n2 E x 2 .
2
E x
2n1
Ex .
n1 n2
3
124.
Электромагнитные волныДля нахождения амплитуды отраженной волны подставим 3 в 1
E x E x
E x
2n1
Ex .
n1 n2
n1 n2
Ex .
n1 n2
4
Из 3 следует, что проекции векторов Е и Е’’ имеют в каждый момент времени
одинаковые знаки. Следовательно, колебания в падающей и в прошедшей во вторую
среду волнах на границе раздела происходят в одинаковой фазе – при прохождении
волны через границу раздела – скачка фазы не происходит.
Другая ситуация для отраженной волны. Из 4 следует, что:
1. При n2 < n1 E x и Ех имеют одинаковые знаки и скачка фазы не происходит при
отражении от оптически менее плотной среды.
2. При n2 > n1 E x и Ех противоположны по знаку, следовательно колебания в
падающей и отраженной волнах на границе раздела происходят в противофазе.
При отражении света от оптически более плотной среды происходит скачок
фазы на π.
Полученный результат справедлив и при наклонном падении световой
волны.
125.
Электромагнитные волныСоотношения, полученные для мгновенных значений проекций световых
векторов справедливы и для амплитуд световых векторов.
E0
Коэффициенты
отражения и
пропускания
2n1
E0 .
n1 n2
E0
n1 n2
E0 .
n1 n2
Найдем коэффициент отражения ρ и коэффициент пропускания τ
световой волны при нормальном падении света.
2
2
n1 n2
1 n21
I n1 E0
.
2
I
n1 E0 n1 n2
1 n21
2
2
2
2
I n2 E0
n2 2n1
.
n
21
2
I
n1 E0
n1 n1 n2
1 n21
2












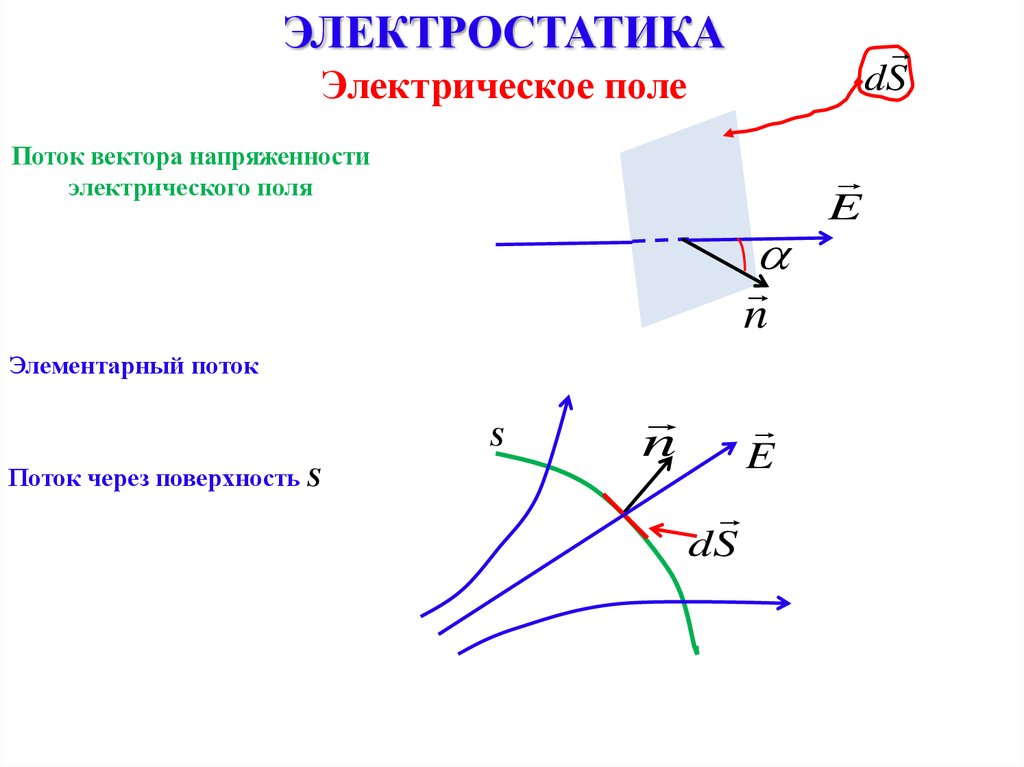








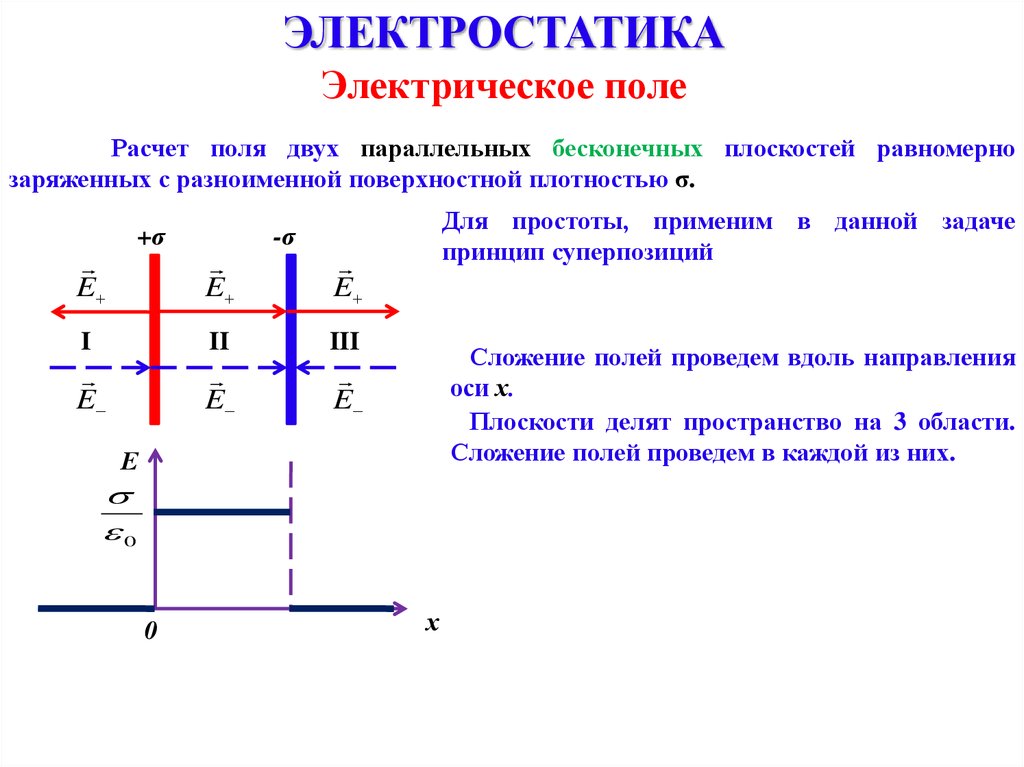






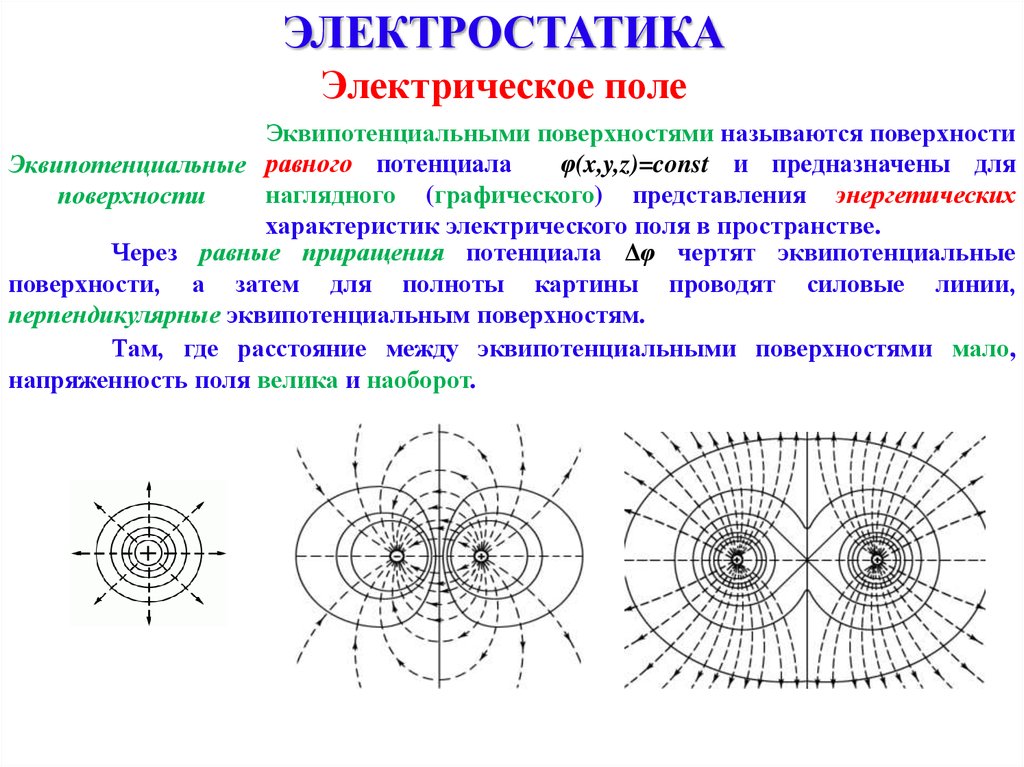
































































































 Физика
Физика








