Построение и анализ частотных характеристик СУ

1. Построение и анализ частотных характеристик СУ

Занятие 1

2.

Основные свойства преобразования Лапласа
1.
Линейность
L{a1 f1(t ) a2 f 2 (t )} a1L{ f1(t )} a2 L{ f 2 (t )} a1F1( p ) a2 F2 ( p ),
2.
Дифференцирование
L{
3.
df (t )
} pF ( p) f (t0 ),
dt
Интегрирование
t
L{ f (t1)dt1}
t0
4.
1
F ( p ).
p
Смещение во времени
L{ f (t τ)} e pτ F ( p).

3.

ЛХ усилительного звена

4.

ЛХ интегрирующего звена
Wр ( jω) =
Kи
;
p
P(ω)=0;
K
Q(ω) = - и ;
ω
Wр ( jω) =
Kи
;
ω
φ(ω)=-90o.

5.

ЛХ дифференцирующего звена
Wр(jω)=Kдjω;
P(ω)=0;
Q(ω)= Kдω; Wр ( jω) = K дω;
φ(ω)=90o.

6.

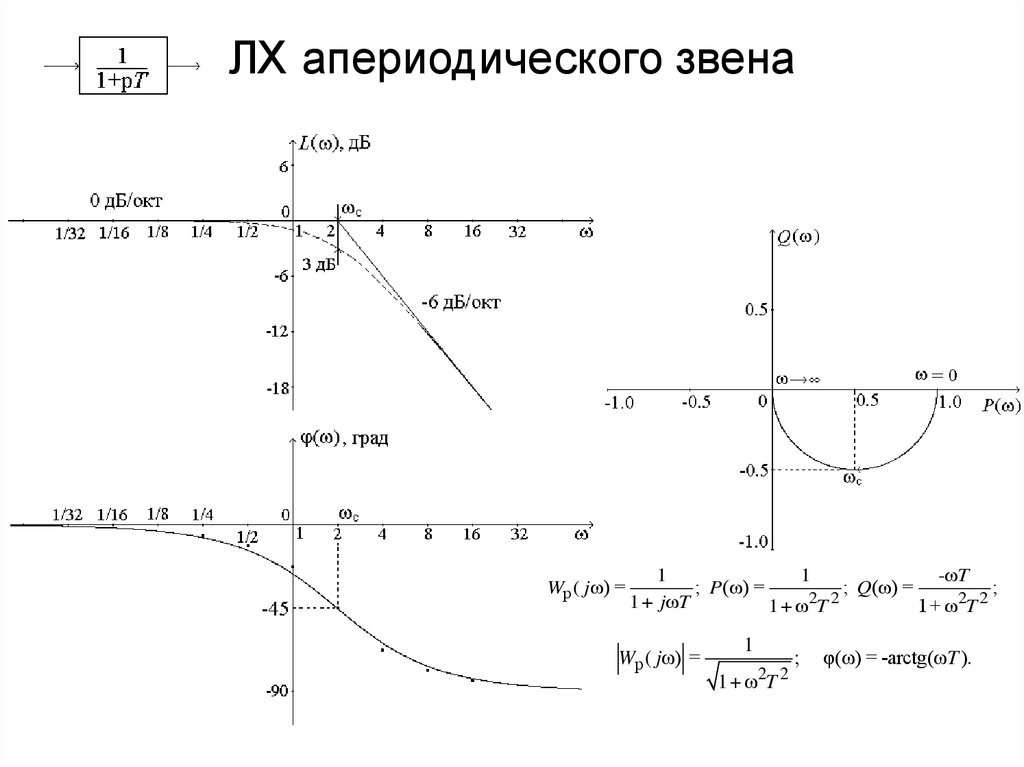
ЛХ апериодического звена
Wр ( jω) =
1
1
-ωT
; P(ω) =
; Q(ω) =
;
2
2
1+ jωT
1+ ω T
1+ ω2T 2
Wр ( jω) =
1
2 2
1+ ω T
;
φ(ω) = -arctg(ωT ).

7.

ЛХ форсирующего звена
АФХ - ?
2 2
Wр ( jω) = 1+ jωT ; P(ω) = 1; Q(ω) = ωT ; Wр ( jω) = 1+ ω T ; φ(ω) = arctg(ωT ).

8.

Пример построения и анализа ЛХ
4(1 0,5 p)
Wр ( p)
.
p(1 2 p)
Экв. схема - ?
АФХ - ?

9.

Характерные точки ЛХ
1. Коэффициент усиления K
(точка пересечения
низкочастотной асимптоты и
оси ординат)
2. Частота среза ωср
Точка пересечения ЛАХ и
оси абсцисс
3. Запас устойчивости по
фазе γ
γ = 180 - |φ (ωср )|
γ > 0 – СУ устойчива
γ < 0 – СУ неустойчива

10.

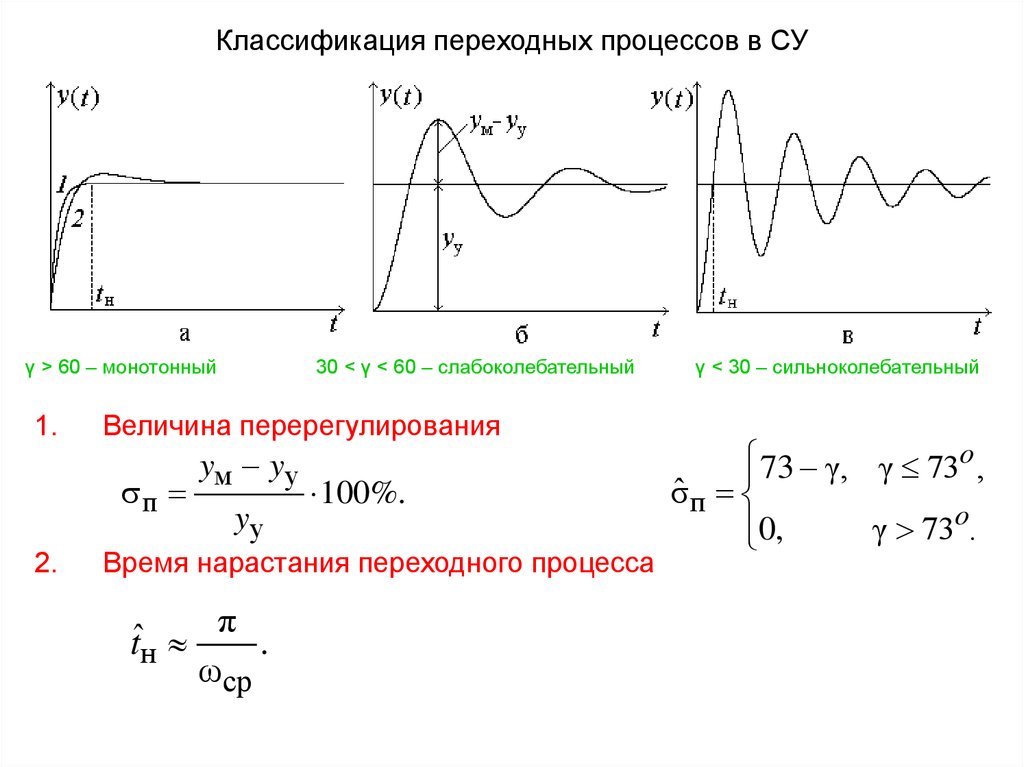
Классификация переходных процессов в СУ
γ > 60 – монотонный
1.
Величина перерегулирования
п
2.
30 < γ < 60 – слабоколебательный
yм yу
yу
100%.
Время нарастания переходного процесса
ˆtн π .
ωср
γ < 30 – сильноколебательный
o
73 γ, γ 73 ,
σˆ п
o
0,
γ
73
.

11.

Типовые соединения звеньев СУ
1. Последовательное
y ( p)
W ( p)
W1( p)W2 ( p).
g ( p)
2. Параллельное
W ( p)
y ( p)
W1( p) W2 ( p).
g ( p)
3. Включение в ООС
y ( p)
W1( p)
W ( p)
.
g ( p) 1 W1( p)W2 ( p )