Похожие презентации:
Развертки поверхностей. (Занятие 13)
1. Занятие 13
2. 1. Развертки поверхностей
Разверткой поверхности называется плоская геометрическаяфигура, полученная в результате совмещения всех точек заданной
(развертываемой) поверхности с плоскостью без изменения
линейных размеров. Необходимым условием совмещения является
отсутствие разрывов и складок.
Развертка поверхностей является основой для построения выкроек
изделий из листового материала, которым затем путем
свертывания и соединения при помощи сварки, пайки или других
сборочных операций придается требуемая форма изделия.
С помощью разверток (точных или приближенных) рассчитывается
площадь поверхности изделий (зданий, сооружений), покрываемых
различными материалами, например окрашиваемых поверхностей.
Поверхности делятся на развертываемые - поверхности
многогранников, цилиндров, конусов и неразвертываемые сферические, торовые.
3.
Развертки могут быть точные, приближенные иусловные.
Точные развертки при обратном преобразовании не
дают разрывов и складок, приближенные и условные
всегда свертываются со складками, либо с разрывами.
Точные развертки строят для поверхностей
многогранников (призмы, пирамиды), приближенные
развертки строят для остальных развертываемых
поверхностей.
Для неразвертываемых поверхностей строят условные
развертки.
4. Свойства разверток:
1. Длины соответствующих линий (ребер, образующих и т.п.) наповерхности и развертке равны;
2. Площадь поверхности, ограниченная определенными линиями,
равна площади развертки, ограниченной теми же линиями;
3. Углы между соответствующими линиями на поверхности и
развертке равны;
4. Прямым линиям на поверхности соответствуют прямые линии
на развертке;
5. Кратчайшей линии между двумя точками на поверхности
соответствует прямая линия на развертке.
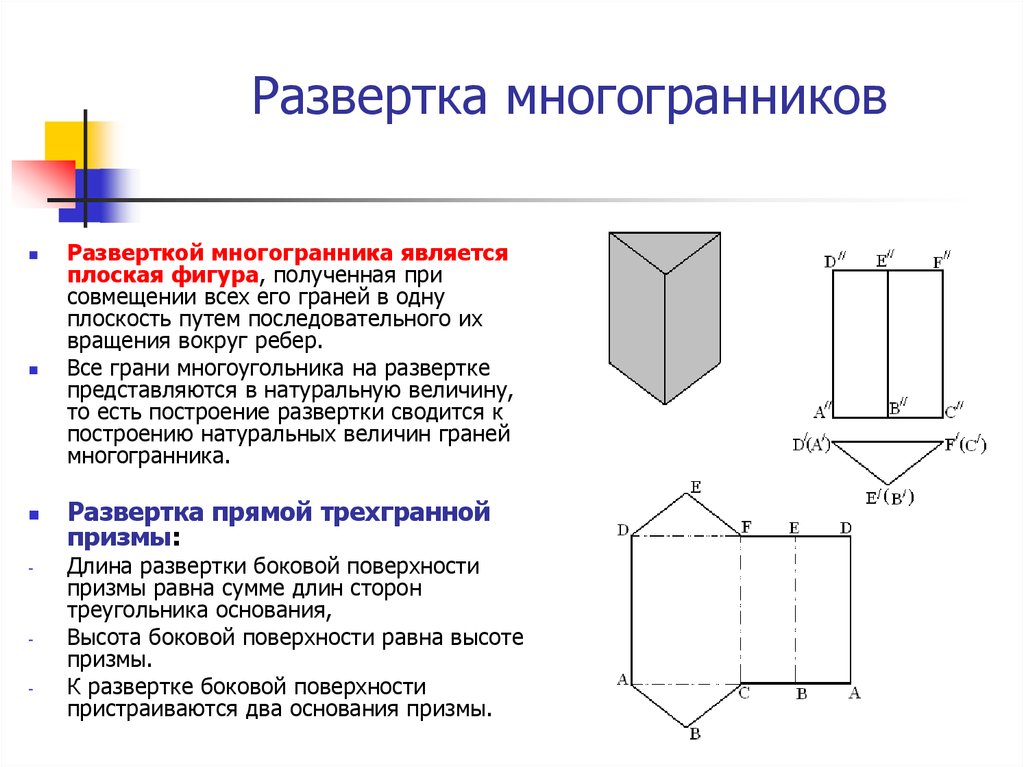
5. Развертка многогранников
--
Разверткой многогранника является
плоская фигура, полученная при
совмещении всех его граней в одну
плоскость путем последовательного их
вращения вокруг ребер.
Все грани многоугольника на развертке
представляются в натуральную величину,
то есть построение развертки сводится к
построению натуральных величин граней
многогранника.
Развертка прямой трехгранной
призмы:
Длина развертки боковой поверхности
призмы равна сумме длин сторон
треугольника основания,
Высота боковой поверхности равна высоте
призмы.
К развертке боковой поверхности
пристраиваются два основания призмы.
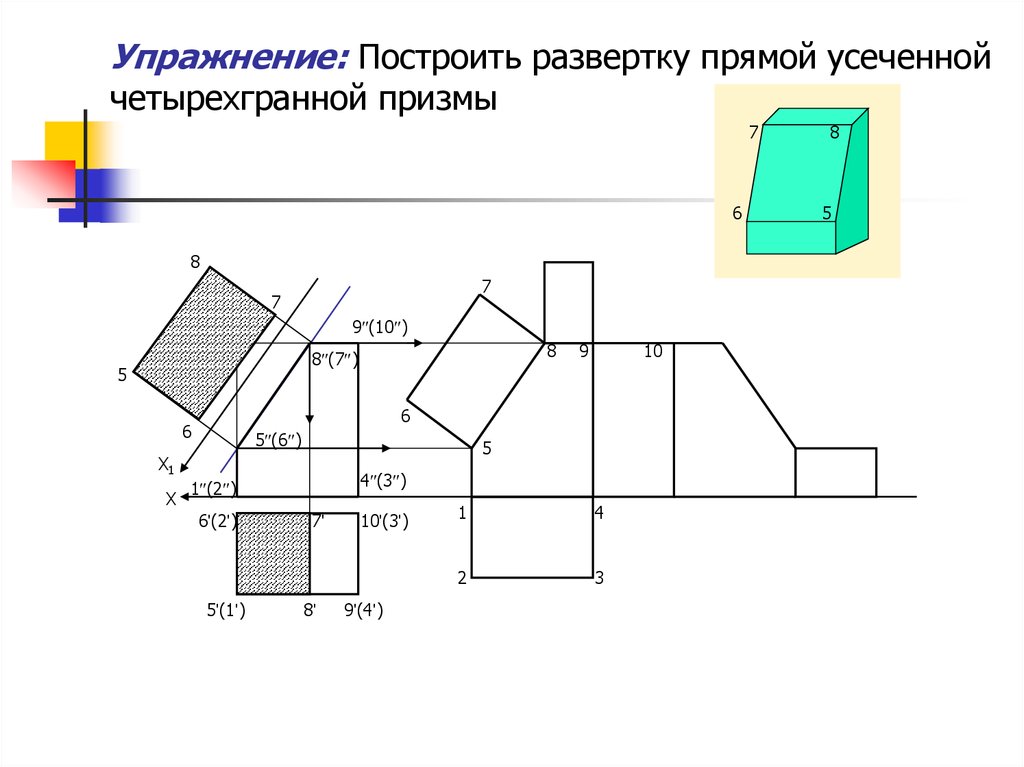
6. Упражнение: Построить развертку прямой усеченной четырехгранной призмы
76
8
7
7
9 (10 )
8
8 (7 )
5
10
6
6
5 (6 )
5
Х1
Х
9
4 (3 )
1 (2 )
6'(2')
5'(1')
7'
8'
10'(3')
9'(4')
1
4
2
3
8
5
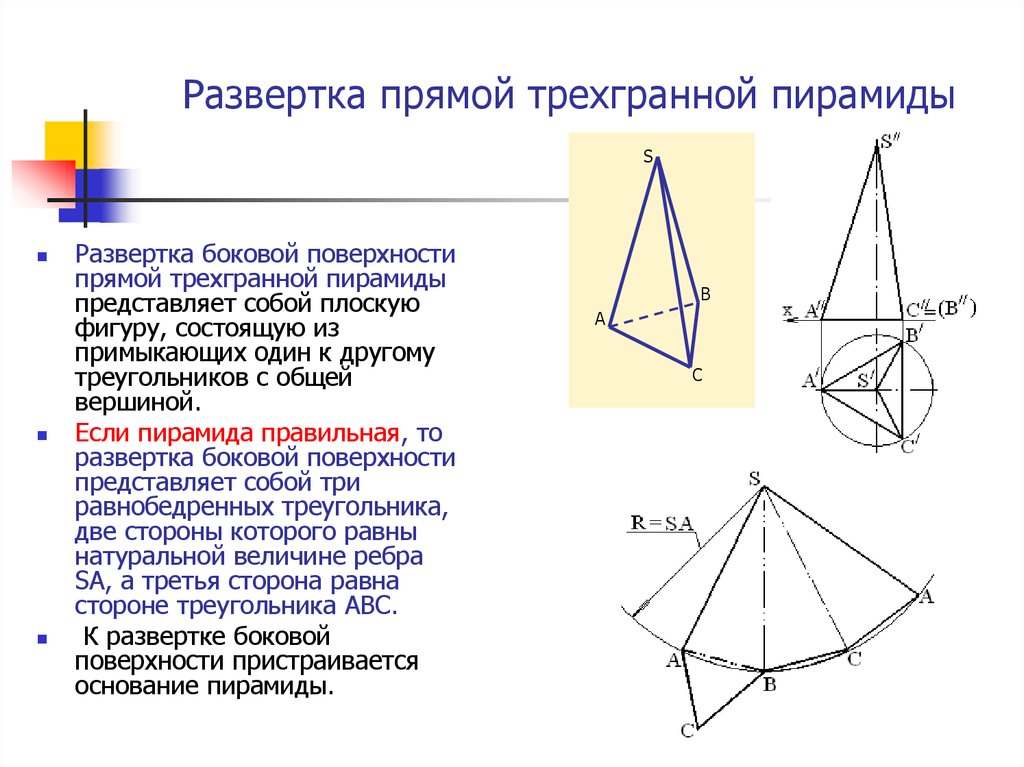
7. Развертка прямой трехгранной пирамиды
SРазвертка боковой поверхности
прямой трехгранной пирамиды
представляет собой плоскую
фигуру, состоящую из
примыкающих один к другому
треугольников с общей
вершиной.
Если пирамида правильная, то
развертка боковой поверхности
представляет собой три
равнобедренных треугольника,
две стороны которого равны
натуральной величине ребра
SA, а третья сторона равна
стороне треугольника АВС.
К развертке боковой
поверхности пристраивается
основание пирамиды.
B
A
C
8.
Упражнение: Построить развертку боковойповерхности наклонной усеченной четырехгранной
пирамиды.
3
4
2
S
2
2
3 (2 )
B
C
x1
1
4 (1 )
x
3
S ''
1
D (A )
B1
C (B )
B'
A'
1'
2'
S'
4'
D'
3'
C'
A1
B
A
4
D
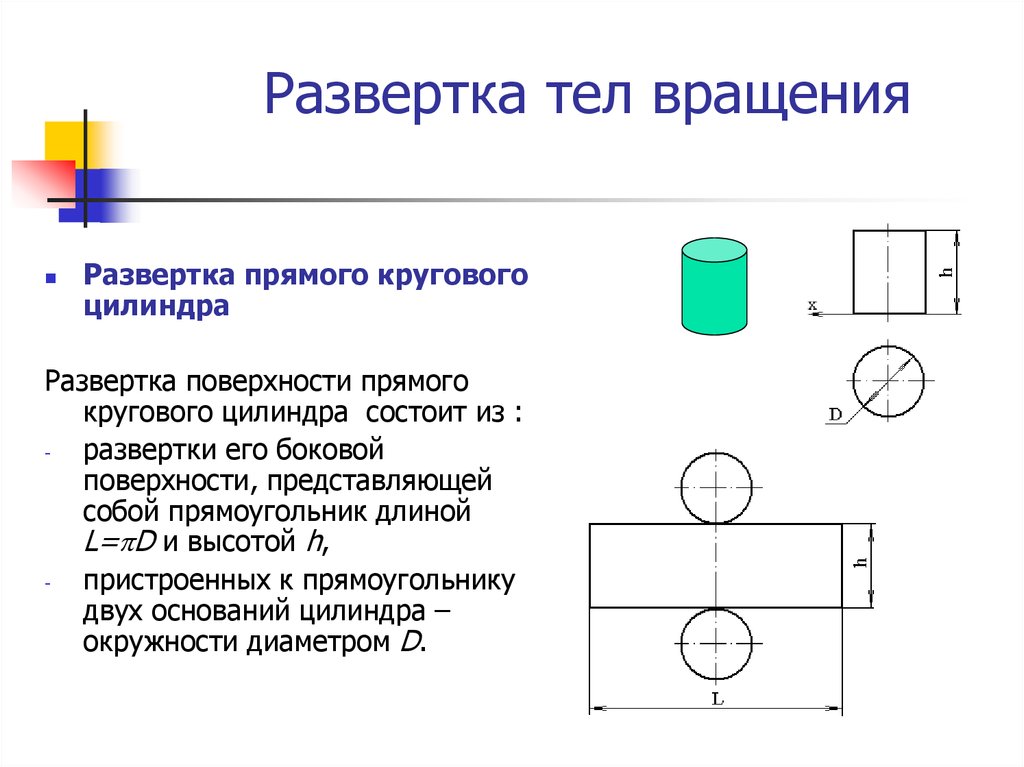
9. Развертка тел вращения
Развертка прямого круговогоцилиндра
Развертка поверхности прямого
кругового цилиндра состоит из :
развертки его боковой
поверхности, представляющей
собой прямоугольник длиной
L= D и высотой h,
пристроенных к прямоугольнику
двух оснований цилиндра –
окружности диаметром D.
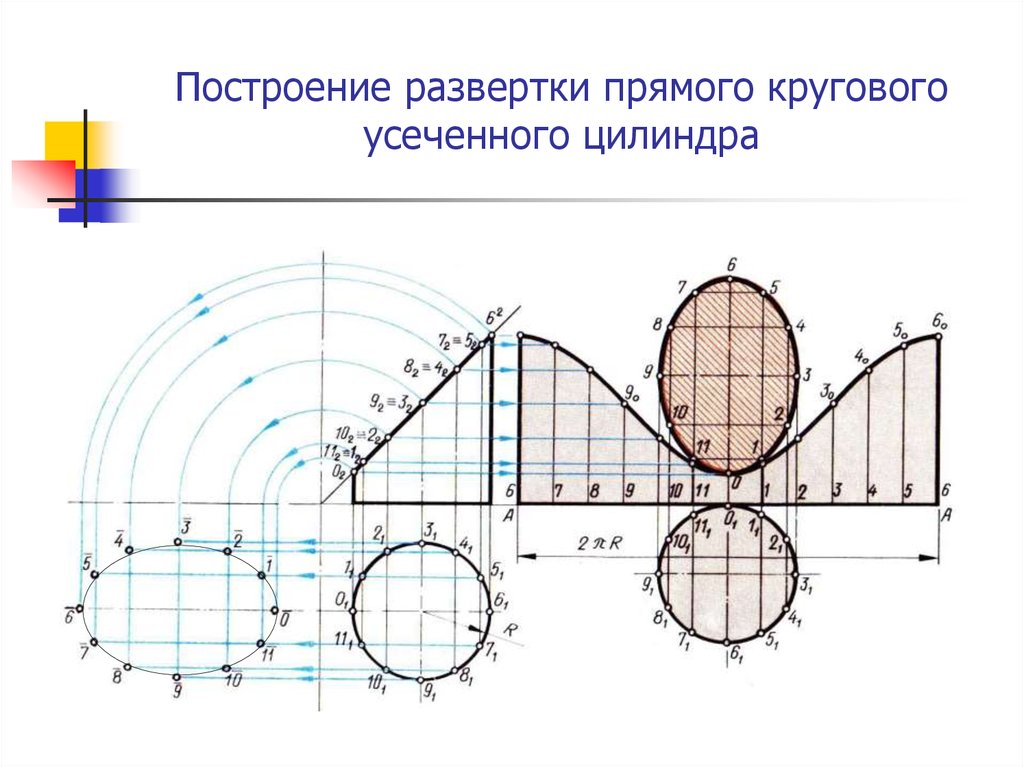
10. Построение развертки прямого кругового усеченного цилиндра
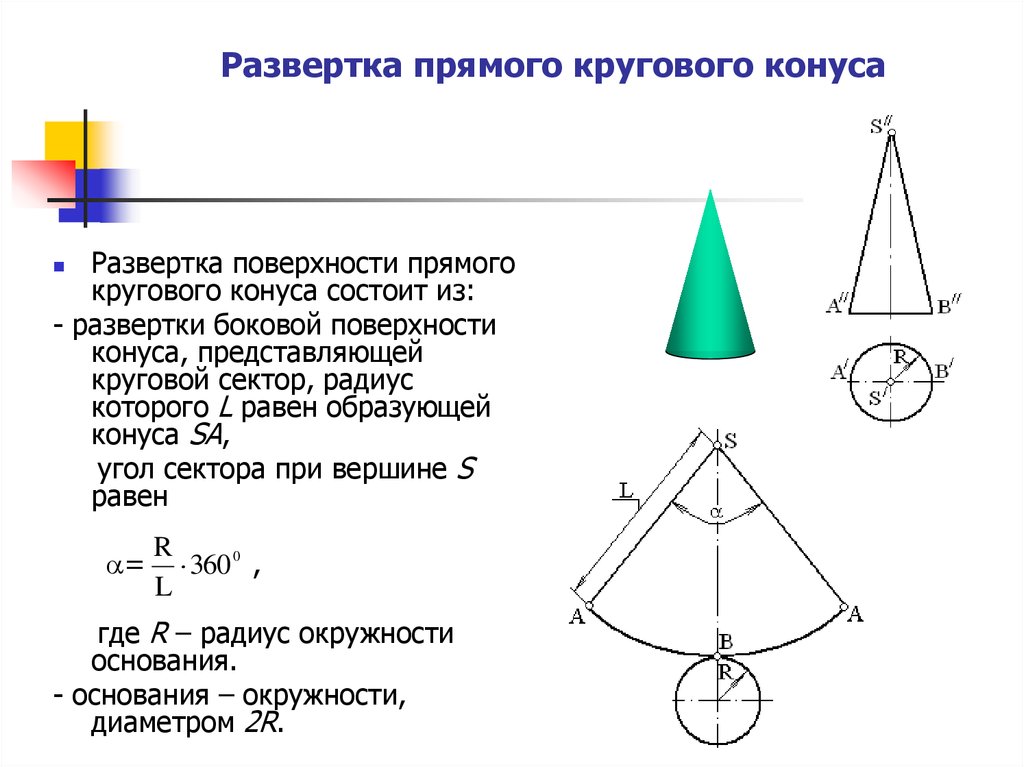
11. Развертка прямого кругового конуса
Развертка поверхности прямогокругового конуса состоит из:
- развертки боковой поверхности
конуса, представляющей
круговой сектор, радиус
которого L равен образующей
конуса SA,
угол сектора при вершине S
равен
=
R
360 0 ,
L
где R – радиус окружности
основания.
- основания – окружности,
диаметром 2R.
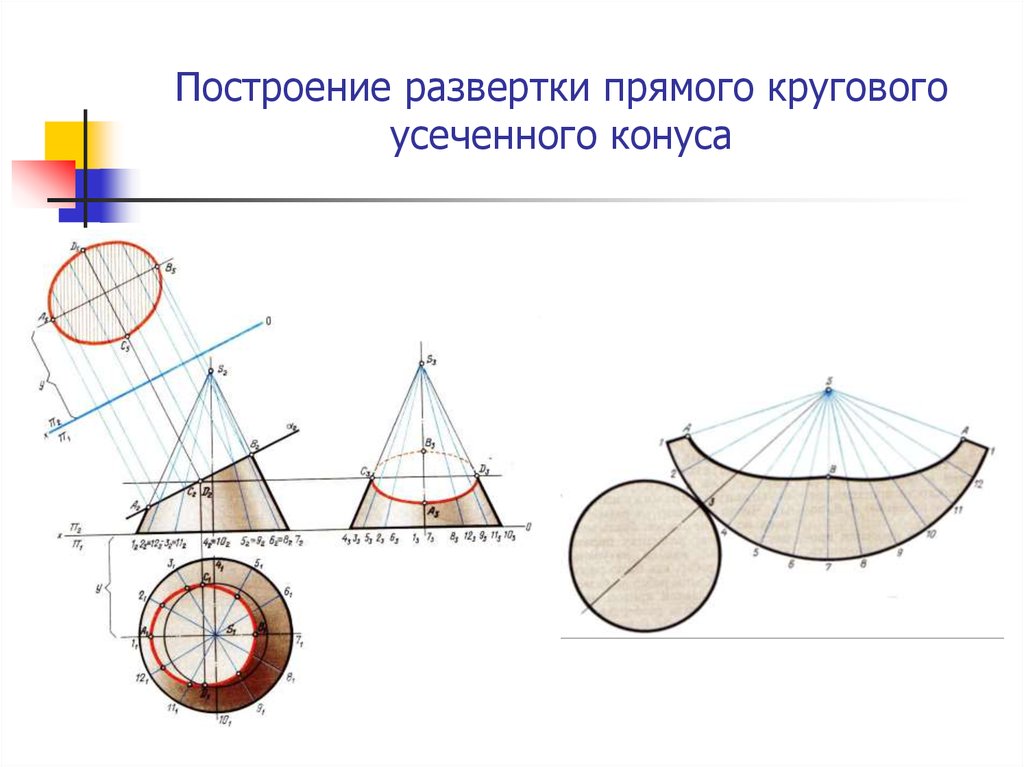
12. Построение развертки прямого кругового усеченного конуса
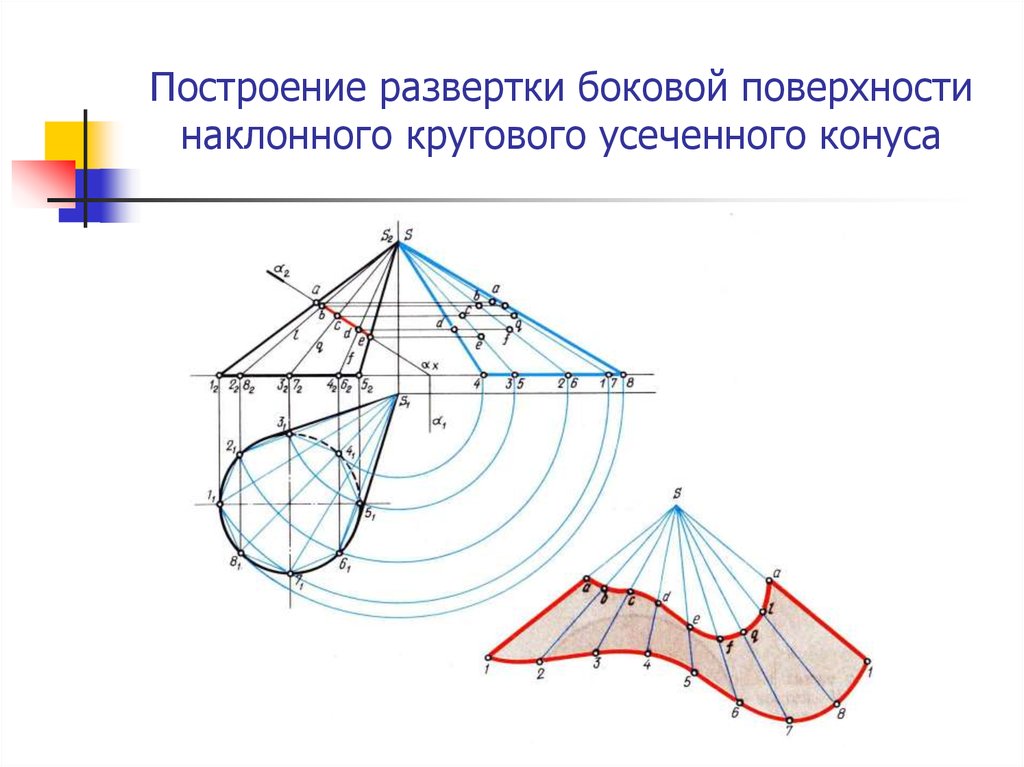
13. Построение развертки боковой поверхности наклонного кругового усеченного конуса
14. Развертка неразвертываемых поверхностей (сфера, тор и т.п)
Для построения разверток неразвертываемых поверхностей отдельные участки этихповерхностей (отсеки) условно заменяют приближенными участками развертываемых
поверхностей. То есть, неразвертываемая поверхность аппроксимируется совокупностью
отсеков поверхностей с известной формой развертки.
Развертка поверхности сферы.
Сначала сфера разбивается на
несколько равных отсеков
горизонтально-проецирующими
плоскостями – по меридианам,
проходящими через ее центр.
Поверхность каждого сферического
отсека аппроксимируется
цилиндрической поверхностью,
направляющей которой является
полуокружность, а образующие
перпендикулярны фронтальной
плоскости проекций.
На рисунке показана условная развертка
сферы, состоящая из 8 частей - равных
разверток конических отсеков,
аппроксимирующих сферу.






 Математика
Математика Инженерная графика
Инженерная графика








