Похожие презентации:
Подготовка к ЕГЭ по математике. Способы отбора корней в тригонометрических уравнениях
1. Подготовка к ЕГЭ по математике
Решение задания 13МБОУ «СОШ № 143»
Г. Красноярск
Князькина Т. В.
2. Способы отбора корней в тригонометрических уравнениях
АрифметическийГеометрический
Алгебраический
Функциональнографический
3.
Арифметический способперебор значений
целочисленного параметра
и вычисление корней.
4.
Найдите все корни уравнения sin 2 x cos x,3
принадлежащие промежутку ; .
sin 2 x cos x;
cos x (2 sin x 1) 0;
cos x 0,
1
sin x ;
2
1) cos x 0
x n; n Z .
2
4
Если n=0,то
3
x ,
;
.
2 2
4
Если n=1,то
3 3
3
x
,
;
.
2
2
4
Если n=-1,то
x
2
,
3
;
.
2
4
Если n=-2,то
3
3
3
x
,
; .
2
2
4
5.
12) sin x ,
2
x
6
2 n
или
5
x
2 n, n Z .
6
Если n=-1, то
11
11
3 или
x
,
;
6
6
4
x
7
7
3
,
;
.
6
6
4
Если n=0, то
x
6
,
3
;
6
4
5 5
3
x
,
; .
6
6
4
или
Если n=1, то
17 17
3
x
,
;
.
6
6
4
13 13
3 или
x
,
;
6
6
4
Ответ :
,
,
2 2 6
.
6.
Алгебраический способа) решение неравенства
относительно неизвестного
целочисленного параметра и
вычисление корней;
б) исследование уравнения с
двумя целочисленными
параметрами.
7.
cos 7 x0.
Решить уравнение :
sin 5 x 1
cos 7 x
0;
sin 5 x 1
cos 7 x 0,
sin 5 x 1 0;
7 x 2 n, n Z ,
5 x 2 k , k Z ;
2
n
x 14 7 , n Z ,
x 2 k , k Z ;
10
5
n
2 k
; n, k Z ;
14
7
10
5
1 n 1 2k
; n, k Z ;
14 7 10 5
8.
Найдём все «неподходящие» n.1 n 1 2k
; n, k Z ;
14 7 10 5
5 10n 7 28k ; n, k Z ;
10n 2 28k ; n, k Z ;
5n 1 14k ; n, k Z ;
1 14k
n
; n, k Z ;
5
4k 1
n 2k
; n, k Z ;
5
9.
k Z,4k 1
a,
a Z.
5
5a 1
k
;
4
a 1
k a
;
4
a Z,
a-1
t;
t Z.
4
a 4t 1;
4k 1
n 2k
; n, k Z ;
5
k 5 t 1;
n 14t 3
t Z , n Z.
Все «неподходящие» n
10. Итак,
cos 7 x0;
sin 5 x 1
х
14
n
7
Ответ:
, n Z ; n 14t 3, t Z.
14
n
7
, n Z ; n 14t 3, t Z.
11. Решить уравнение
2 sin x 3 cos x 3 0.2
Укажите корни,
принадлежащие отрезку 4 ;5 .
12.
2 sin x 3 cos x 3 0;2
2 ( 1 c o s x ) 3 cos x 3 0;
2
2 2 cos x 3 cos x 3 0;
2
2 cos x 3 cos x 1 0;
2
2 cos x 3 cos x 1 0;
2
13.
2 cos x 3 cos x 1 0;, ,n
n
22 ,nnn
n ZZ
Z.
32))1xx) x 2
1
33
2
cos x 2 ,
cos x 1;
x 3 2 n,
x 2 n, n Z .
13
x
.
3
x 4 .
n=2
2 5n , n5
,Zn; Z ;
4 4 1
2
n
54 , n; Z ;
43) x 32 n
3
1
, n5
Z ; Z ;
1 4 2 n 2 n5
4
,
n
4 23n 13
5, n Z ;
. Z;
32 xn 5 , n
1
1
3
2
1
1
, nZ ; Z ;
4 4 32 n2 n5 5 , n3
3 2 n 2 1 3, n Z ;
24 1 2n 2521 , n Z ;
3 32n 4 ,3n Z ;
3 n 2. 3
513 n 116 , n Z ;
1 6 n 2 6, n Z ;
6
3
1
2
n2 6 2.n 2 3 , n Z ;
нет значений.
Ответ :
2 n,
3
13
2 n, n Z ;
; 4 .
3
14.
Геометрический способ:а) изображение корней на
тригонометрической окружности
с последующим их отбором на
заданном промежутке;
б) изображение корней на
координатной прямой с
последующим отбором с учетом
имеющихся ограничений.
15.
2 cos x 3 cos x 1 0;2
Выполним отбор корней в
уравнении по
предыдущем
x
2
n
,
n
Z
;
4
другому
!
3
x 2 k , k Z .
Ответ :
53
y
1
7
13
3 3
3
04
2рад
-1
2 n , n Z ;
3
13
2 k , k Z ;
; 4 .
3
;5
0
0,5
1
5
11
333
16. Решить уравнение
2 sin 2x cos x 4 sin x 1 0.Укажите корни,
5 7
; .
принадлежащие отрезку 2 2
17.
2 sin 2 x cos x 4 sin x 1 0;2 2 sin x cos x cos x 4 sin x 1 0;
4 sin x cos x cos x 4 sin x 1 0;
cos x (4 sin x 1) (4 sin x 1) 0;
s in 2 x 2 s in x c o s x
(4 sin x 1) (cos x 1) 0;
0, множитель
4 sin x 1 общий
cos x 1 0;
1
sin x 4 ,
cos x 1;
общий множитель
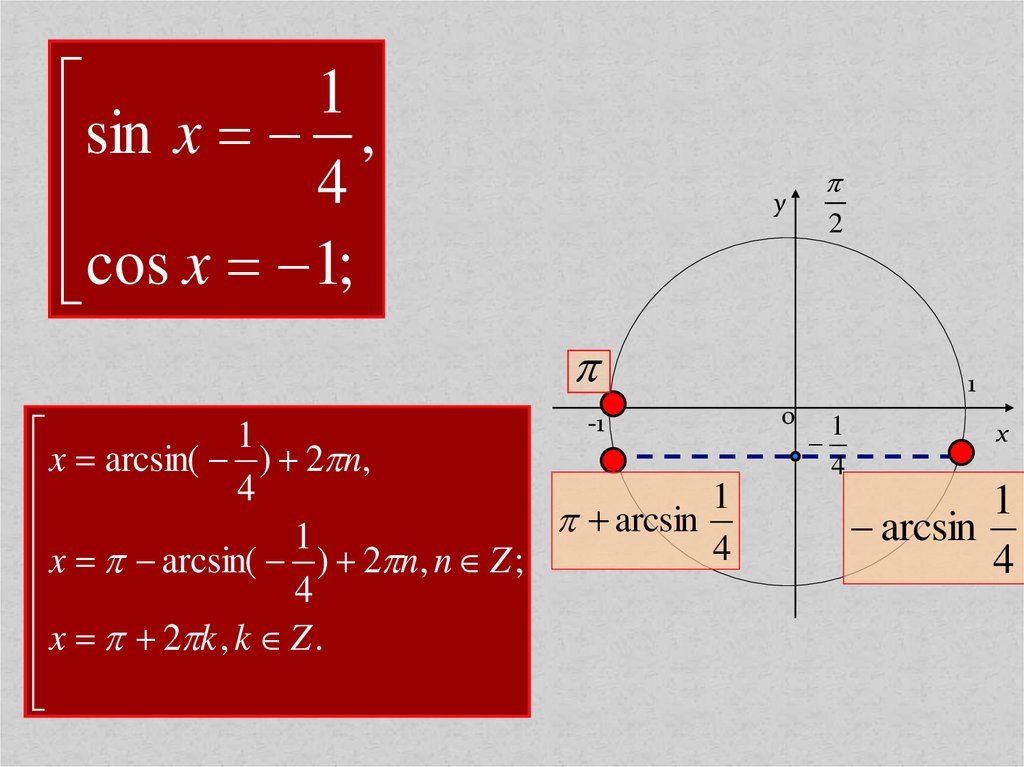
18.
1sin
x
,
4
cos x 1;
y
2
1
x arcsin( 4 ) 2 n,
1
arcsin
1
x arcsin( ) 2 n, n Z ;
4
4
x 2 k , k Z .
-1
1
0
1
4
x
1
arcsin
4
19.
11
x
arcsin
2
n
,
x 3 4 arcsin ,
x arcsin 1 2 n, n 4
Z;
4
x
3
.
2 k , k Z .
x
2
1
-1
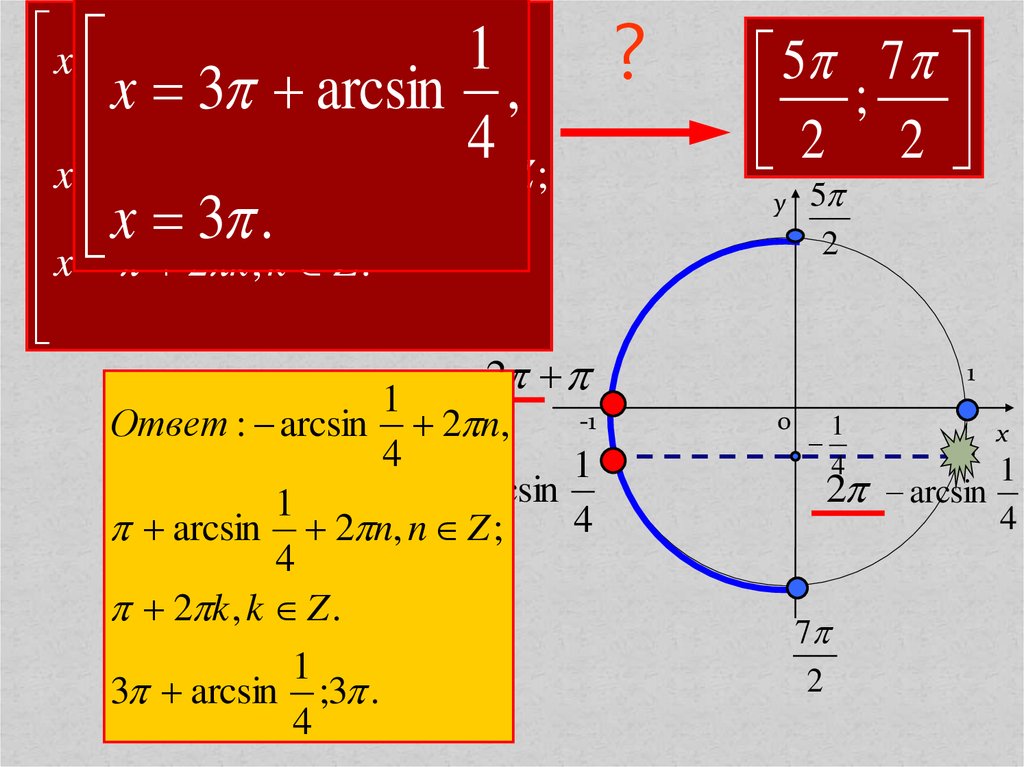
Ответ : arcsin 2 n,
4
1
1 2 arcsin 4
arcsin 2 n, n Z ;
4
2 k , k Z .
1
3 arcsin ;3 .
4
?
5 7
;
2 2
y
5
2
1
0
1
4
2
7
2
x
1
arcsin
4
20. Решить уравнение
2 sin x sin x cos x 3 cos x 0.2
Укажите корни,
принадлежащие отрезку
2
3
;
2 2
.
21.
2 sin x sin x cos x 3 cos x 0.2
2
2tg x tgx 3 0;
2
tgx 1,
О
д
н
о
р
о
д
н
о
е
у
р
а
в
н
е
н
и
е
Разделим
на
3
tgx ; cos x; cos x≠0.
2
2
2
x
n
,
n
Z
;
4
x arctg 3 k , k Z .
2
22.
x 4 n, n Z ;x arctg ( 3 ) k , k Z .
2
3
arctg
2
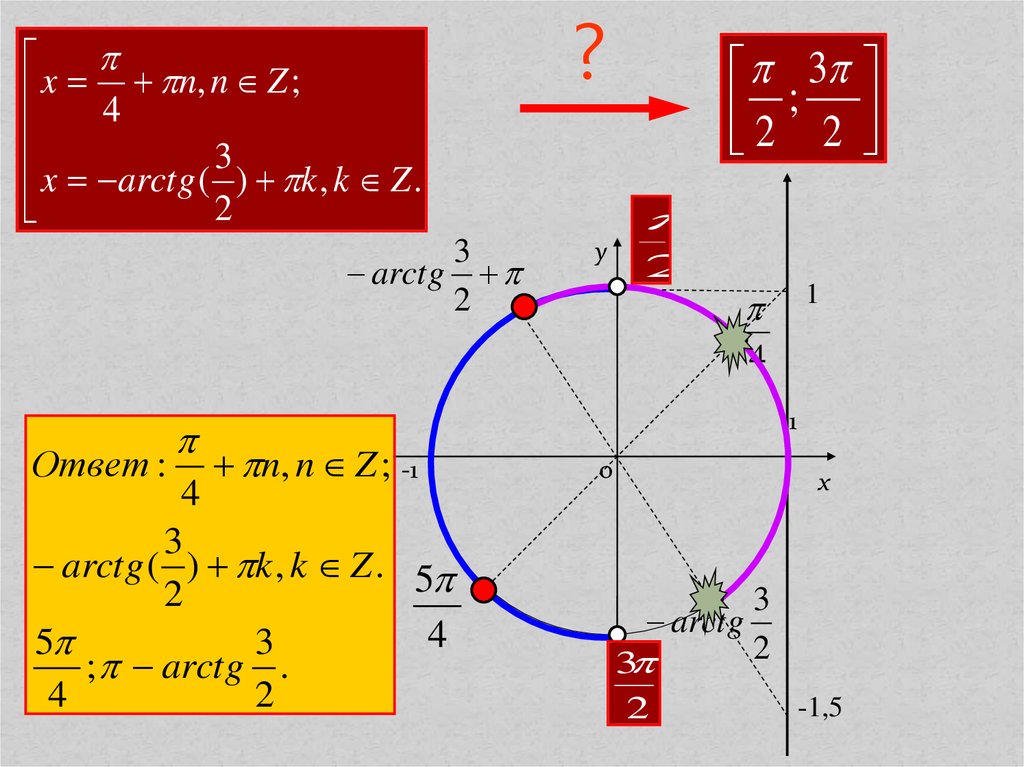
Ответ :
?
3
2 ; 2
y
2
4
1
1
n, n Z ; -1
4
3
arctg ( ) k , k Z . 5
2
4
5
3
; arctg .
4
2
0
x
3
arctg
2
3
2
-1,5
23. Отбор корней на координатной прямой.
xcos
2 0.
x
sin
3
Решение :
x
cos 2 0,
sin x 0;
3
0
x 2 k , k Z ,
x 3 n, n Z .
3
x
T (cos ) 4 ,
2
x
T (sin ) 6 .
3
Наим. общий период :
Т общ 12 .
7
9
5
Ответ :
6 т, 6 т, т Z .
1 1
х
24.
Функционально-графическийспособ
выбор корней с использованием
графика простейшей
тригонометрической функции.
25. Решите уравнение
2sin 2 x 2 sin x cos x
2 0;
2 sin x 1
2
2 sin x cos x 2 sin x cos x
2 0;
2 sin x 1
2
(cos x
) (2 sin x 1)
2
0;
2 sin x 1
2
cos
x
,
2
1
sin x ;
2
1
sin x ;
2
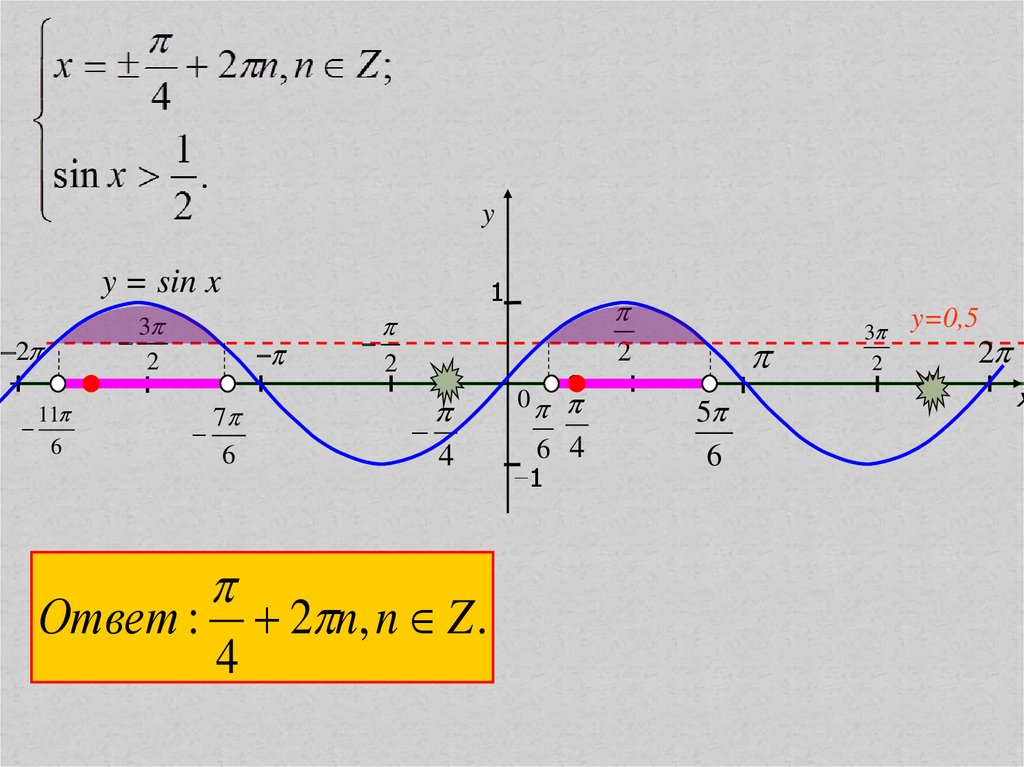
x 4 2 n, n Z ;
sin x 1 .
2
26.
yy = sin x
2
11
6
3
2
1
7
6
2
2
4
Ответ : 2 n, n Z .
4
6 4
0
−1
5
6
3
2
y=0,5
2
x
27.
Дано уравнение:а) Решите уравнение.
б) Укажите корни уравнения, принадлежащие отрезку
Решение:
Тогда cos x = 0
или sin x = 0,5
28.
Найдём корни уравнения, принадлежащие отрезкуИтак, первый корень:
Решаем неравенство:
Так число k целое, то k1 = 2 k2 = 3
Находим корни, принадлежащие интервалу:
Следующий корень:
29.
Решаем неравенство:Для полученного неравенства целого числа k не существует.
Следующий корень:
Решаем неравенство:
30.
Так как число k целое, то k = 1.Находим корень принадлежащий интервалу:
Ответ:
31. В презентации использовались ресурсы:
http://alexlarin.net/ege/2012/C12012.pdf2. ЕГЭ-2012.Математика: типовые
экзаменационные варианты: 30
вариантов/ под ред. А.Л. Семёнова,
И.В.Ященко.-М.: Национальное
образование, 2011. (ЕГЭ -2012. ФИПИ –
школе).





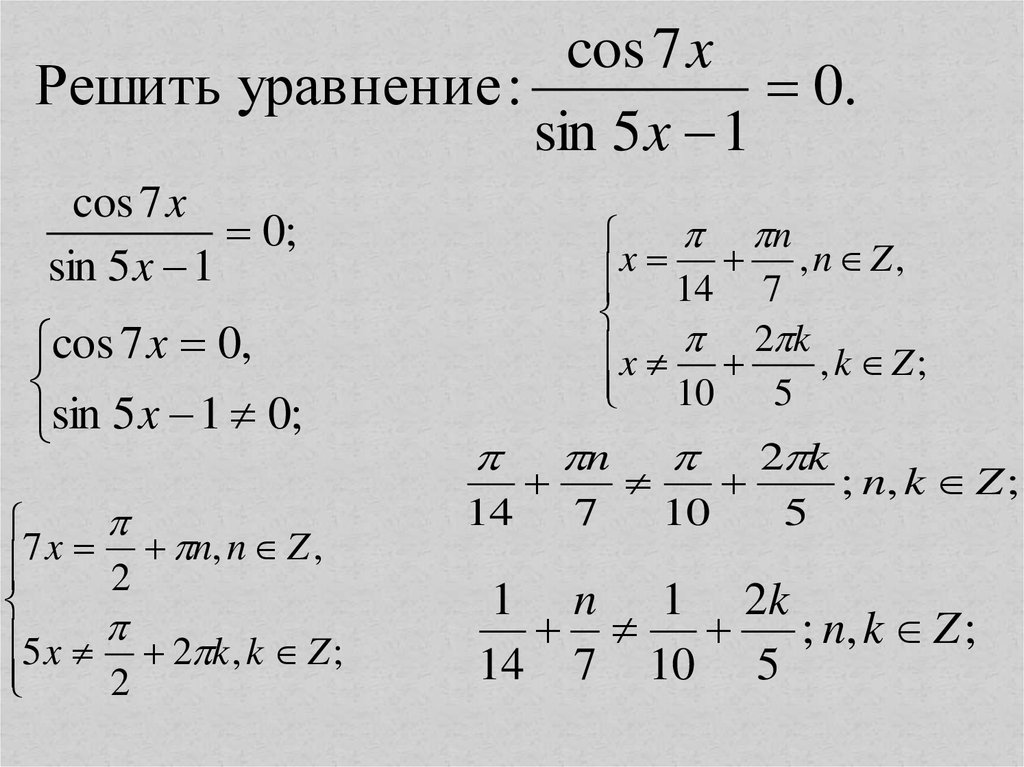


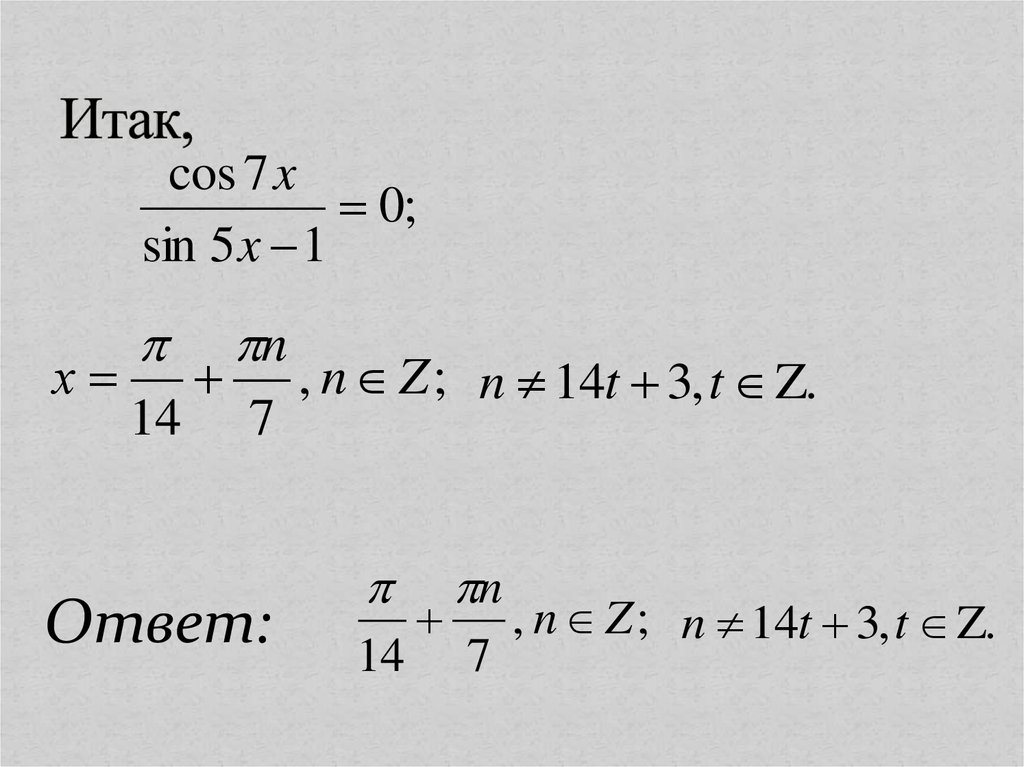

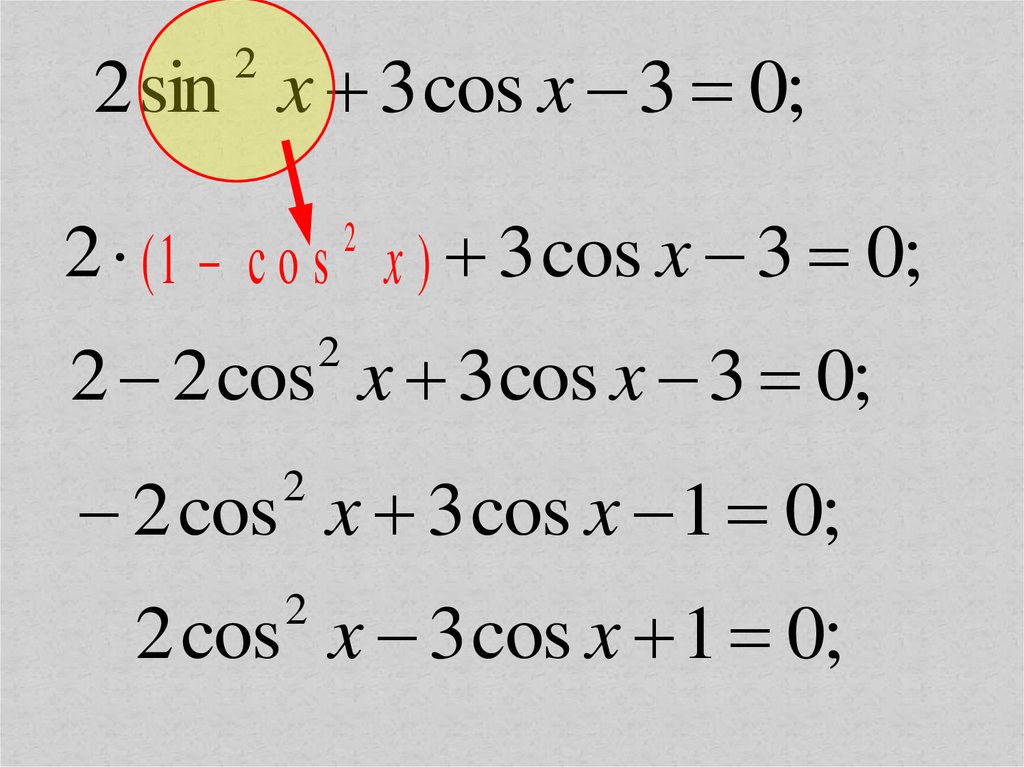















 Математика
Математика








