Первообразная. Интеграл

1. Первообразная Интеграл

МОУ СОШ № 5 – «Школа здоровья и развития»
Первообразная
Интеграл
Автор: Елена Юрьевна Семёнова

2. Содержание

Понятие первообразной
Неопределенный интеграл
Таблица первообразных
Три правила нахождения первообразных
Определенный интеграл
Вычисление определенного интеграла
Площадь криволинейной трапеции
Площадь криволинейной трапеции (1)
Площадь криволинейной трапеции (2)
Площадь криволинейной трапеции (3)
Площадь криволинейной трапеции (4)
Пример (1)
Пример (2)

3. Понятие первообразной

Функцию F(x) называют первообразной для
функции f(x) на интервале (a; b), если на нем
производная функции F(x) равна f(x):
F ( x ) f ( x )
Операцию, обратную дифференцированию
называют интегрированием.

4.

Примеры
1. f(x) = 2x; F(x) = x2
F (x)= (x2) = 2x = f(x)
2. f(x) = – sin x; F(x) = сos x
F (x)= (cos x) = – sin x = f(x)
3. f(x) = 6x2 + 4; F(x) = 2x3 + 4x
F (x)= (2x3 + 4x) = 6x2 + 4 = f(x)
4. f(x) = 1/cos2 x; F(x) = tg x
F (x)= (tg x) = 1/cos2 x= f(x)

5. Неопределенный интеграл

Неопределенным интегралом от непрерывной
на интервале (a; b) функции f(x) называют
любую ее первообразную функцию.
f
(
x
)
dx
F
(
x
)
c
Где С – произвольная постоянная (const).

6.

Примеры
1. Adx Ax C ; Ax C A
x
x
x
x
2. e dx e С; e C e
3. sin xdx cos x С ;
4
x
4. x dx
С;
4
3
cos x C
sin x
tg x C
1
2
cos x
x
1
С 4x 3 x 3
4
4
1
5.
dx tg x C ;
2
cos x
4

7. Таблица первообразных

F(x)
x n 1
C
n 1
2x x
C
3
sin x C
cos x C
tgx C
ctgx C
f(x)
x
n
х
cos x
sin x
1
сos 2 x
1
sin2 x
F(x)
f(x)
a C
ax
lna
1
C
x
ln x
ex C
ex
x
C
Cx
loga x C
1
x lna
arcsin x C
1
1 x2

8.

Три правила нахождения
первообразных
1º Если F(x) есть первообразная для f(x), а G(x) –
первообразная для g(x), то F(x) + G(x) есть
первообразная для f(x) + g(x).
2º Если F(x) есть первообразная для f(x), а k –
постоянная, то функция kF(x) есть первообразная
для kf(х).
3º Если F(x) есть первообразная для f(x), а k и b –
1
постоянные, причем k ≠ 0, то функция
F(kx + b)
k
есть первообразная для f(kx + b).

9. Физический смысл первообразной

10. Определенный интеграл

b
f x dx F x
b
a
F b F a
a
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла
заключается в том, что определенный интеграл
равен
площади
криволинейной
трапеции,
образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.

11. Вычисление определенного интеграла

3x
2
2
2 x 1 dx x x x
3
2
2
1
1
23 22 2 13 12 1 6 1 5
10
3
2 x 6 x 6
x 6 dx
3
10
3
2 10 6 10 6 2 3 6 3 6 80
2
18 7
3
3
3
3

12. Площадь криволинейной трапеции

y
D
C
b
S ABCD f x dx
a
a
b
B
x=b
x=a
0
A
F b F a
y=0
x

13. Площадь криволинейной трапеции (1)

y
B
b
y=0
x
b
S ABCD f x dx
D
C
x=b
a
x=a
0
A
a
F a F b

14.

y
Площадь криволинейной
трапеции (2)
D
C
S PMCD S ABCD S ABMP
P
0
Aa
M
b B
b
b
a
a
f x dx g x dx
f x g x dxx
b
a

15.

y
Площадь криволинейной
трапеции (3)
D
0
A
a
P
C
S PMCD S ABCD S ABMP
B
b
M
b
b
a
a
x
f x dx g x dx
b
f x g x dx
a

16. Пример 1:

вычислить площадь фигуры,
ограниченной линиями y = x2, y = x + 2.
y
SВОС SABCD SABOCD
C
2
2
1
1
x 2 dx x 2 dx
B
A
-1
2
2
x
x
х 2 х 2 dx 2x
3
2
1
O
D
2
2
3
2
1
8 1
1
1
2 4 2 5 4,5
3 2
3
2
x

17.

y
Площадь криволинейной
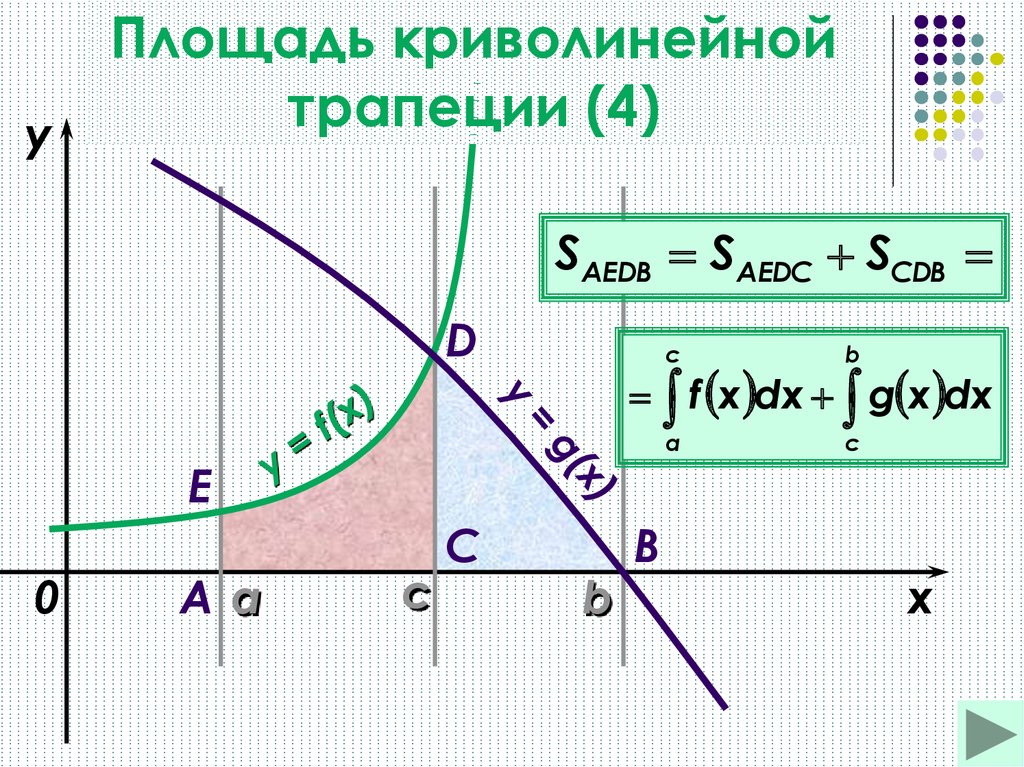
трапеции (4)
SАЕDВ SAEDC SСDB
D
с
b
a
с
f x dx g x dx
Е
0
Aa
с
C
b
B
x

18.

вычислить площадь фигуры,
Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
y
4
0
SАDВ SADС SСDB
D
A
2
4
C
8
B
x

19.

вычислить площадь фигуры,
Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
4
8
x - 2 dx 2
2
2
4
3 4
x 2
8 - хdx
3
4 8 x 8 x
3
2
8
4
4 2 3 2 2 3 4 8 8 8 8 4 8 4 8 4
3
3
3
3
8 32 40
1
13
3 3
3
3