Оптимізаційні методи та моделі. Нелінійні задачі оптимізації. Метод множників Лагранжа. (Тема 12)

1. Оптимізаційні методи та моделі

Університет митної справи та фінансів
Оптимізаційні
методи та моделі
доц. Лебідь О.Ю.
Дніпропетровськ
2016

2. Тема 12: Нелінійні задачі оптиміза- ції. Метод множників Лагранжа

Тема 12: Нелінійні задачі
оптимізаПлан
ції. Метод множників Лагранжа
1.
Умовний
та
безумовний
екстремуми функцій
2. Ідея методу множників Лагранжа
3. Метод множників Лагранжа
4. Приклад
5. Узагальнений метод множників
Лагранжа
6.
Необхідні
умови
існування
сідлової точки
2

3. Методи розв’язання задач нелінійної оптимізації

Методи
розв’язування
задач
нелінійної
оптимізації бувають прямі та непрямі.
За допомогою прямих методів знаходження
оптимальних планів здійснюють у напрямку
найшвидшого збільшення (зменшення) значення
цільової функції. Типовим представником цієї
групи методів є градієнтні. Методика застосування
непрямих методів передбачає зведення задачі до
такої, оптимум якої слід знаходити простішими
методами.
3

4. Математична постановка задачі нелінійної оптимізації

Найпростішими для розв’язування є задачі
нелінійної оптимізації, в яких система обмежень
складається лише з рівнянь.
Знайти
z z ( x1, x2 ,..., xn ) max(min)
(1)
за умов
g i ( x1 , x2 ,..., xn ) bi (i 1, m ),
(2)
x j 0 ( j 1, n) .
(3)
Якщо хоча б одна з функцій ( z ( x1 , x2 ,..., xn ) або
g i ( x1 , x2 ,..., xn ) , i 1, m ) є нелінійною.
4

5. Умовний та безумовний екстремуми функцій

У безумовних нелінійних задач оптимізації
локальний
та
глобальний
екстремуми
визначаються з необхідних та достатніх умов
існування екстремуму функції.
5

6. Умовний та безумовний екстремуми функцій

Необхідна
умова
існування
локального
екстремуму функції двох змінних формулюється:
для того, щоб точка ( x10 , x20 ) була точкою локального
екстремуму, необхідно, щоб функція f ( x1 , x2 ) була
неперервною і диференційовною в околі цієї точки
і перші частинні похідні за змінними x1 та x2 у цій
точці дорівнювали нулю:
f ( x10 , x20 ) f ( x10 , x20 )
0
.
x1
x2
Точка ( x10 , x20 ) називається критичною.
6

7. Умовний та безумовний екстремуми функцій

Достатня
умова
існування
локального
екстремуму функції двох змінних: для того, щоб
0
0
(
x
,
x
критична точка 1 2 ) була точкою локального
екстремуму, достатньо, щоб функція f ( x1 , x2 ) була
визначена в околі критичної точки ( x10 , x20 ) та мала в
цій точці неперервні частинні похідні другого
порядку.
7

8. Умовний та безумовний екстремуми функцій

2
Тоді, якщо
точці
( x10 , x20 )
2 f ( x10 , x20 ) 2 f ( x10 , x20 ) 2 f ( x10 , x20 )
0,
2
2
x1
x2
x1 x2
функція
причому, якщо
f ( x1 , x 2 )
2 f ( x10 , x20 )
0
2
,
x1
тоді
то в
має екстремум,
( x10 , x 20 )
– точка
локального максимуму функції f ( x1 , x2 ) , а якщо
2 f ( x10 , x 20 )
0
2
,
x1
тоді
( x10 , x20 )
–
точка локального
мінімуму функції f ( x1 , x2 ) .
8

9. Умовний та безумовний екстремуми функцій

У разі, якщо
2
2 f ( x10 , x20 )
2
x
1
то в точці
Якщо
2 f ( x10 , x20 ) 2 f ( x10 , x20 )
0,
2
x2
x1 x2
( x10 , x20 ) функція f ( x1 , x 2 ) екстремуму не має.
f
2
( x10 , x 20 )
x12
f
2
( x10 , x20 )
2
x2
2
0
0
( x1 , x2 )
f
x1 x2
2
0,
то питання про існування екстремуму залишається
відкритим.
9

10. Приклад задачі двох змінних умовної нелінійної оптимізації

Знайти
max (min) f ( x1 , x 2 )
(4)
за умови, що
q ( x1 , x2 ) b .
(5)
Найпростіший спосіб розв’язання задачі такого
виду полягає в тому, що спочатку з обмеження (5)
знаходять вираз однієї змінної через іншу.
10

11. Приклад задачі двох змінних умовної нелінійної оптимізації

Наприклад, визначають x2 через x1 . Отриманий
вираз виду x2 g ( x1 ) підставляють у функцію (4), що
після цього стає функцією однієї змінної f ( x1 , g ( x1 )) , і
далі знаходять її безумовний екстремум.
x
Якщо деяка точка 1 є точкою екстремуму
функції f ( x1 , g ( x1 )) , то точка X ( x1 , x2 g ( x1 )) є точкою
умовного екстремуму функції (4) за умови (5).
11

12. Приклад задачі двох змінних умовної нелінійної оптимізації

Однак
не завжди
вдається
відшукати
аналітичний вираз однієї змінної через іншу в умові
(5). Часто це досить важко здійснити або
неможливо. Також іноді складно узагальнити даний
спосіб для функції n змінних, на які накладено m
обмежень. Тому описана досить проста ідея
зведення задачі відшукання умовного екстремуму
функції кількох змінних до задачі на безумовний
екстремум функції однієї змінної не може бути
використана як основа універсального методу
розв’язування задач на умовний екстремум.
12

13. Ідея методу множників Лагранжа

Ідея методу множників Лагранжа полягає в
заміні початкової задачі простішою.
Від початкової
задачі
пошуку умовного
екстремуму переходимо до задачі відшукання
безумовного екстремального значення іншої
функції. Отже, завдяки такому перетворенню
можливе
застосування
методів
класичного
знаходження екстремуму функції кількох змінних.
13

14. Метод множників Лагранжа

Знайти
за умов:
max min Z f x1 ,
qi x1 ,
x2 , ...,
xn
(6)
x2 , ..., x n bi i 1, m ,
(7)
де функції f x1 , x 2 , ..., xn і qi x1 , x2 , ..., xn мають
бути диференційовними.
Задача (6)-(7) полягає в знаходженні екстремуму
функції f (x) за умов виконання обмежень qi , (i 1, m) .
14

15. Метод множників Лагранжа

Переходимо до задачі пошуку безумовного
екстремуму. Теоретично доведено, що постановки
та розв’язання таких задач еквівалентні.
Замінюємо цільову функцію (6) на складнішу. Ця
функція називається функцією Лагранжа і має
такий вигляд:
m
L x1 , x2 ,..., xn , 1 , 2 ,..., m f ( x1 , x2 ,..., xn ) i (bi qi ( x1 , x2 ,..., xn )),
(8)
де i – деякі невідомі величини, що називаються
множниками Лагранжа.
i 1
15

16. Метод множників Лагранжа

Знайдемо частинні похідні і прирівняємо їх до
нуля:
L
x 0,
j
L
0,
i
j 1, n ;
i 1, m .
f ( x1 , x2 ,..., xn ) m qi ( x1 , x2 ,..., x n )
i
0 j 1, n ;
x j
x j
i 1
i 1, m .
bi qi ( x1 , x2 ,..., xn ) 0,
(9)
Друга група рівнянь системи (9) забезпечує
виконання умов (7) початкової задачі нелінійної
оптимізації.
Система (9), як правило, нелінійна.
16

17. Метод множників Лагранжа

Розв’язками (9) є X ( x1 , x2 ,..., xn ) і ( 1 , 2 ,..., m ) –
стаціонарні точки. Оскільки, ці розв’язки отримані
з необхідної умови екстремуму, то вони визначають
максимум, мінімум задачі (6)-(7) або можуть бути
точками перегину (сідловими точками).
Для діагностування стаціонарних точок і
визначення типу екстремуму необхідно перевірити
виконання достатніх умов екстремуму, тобто
дослідити
в
околі
стаціонарних
точок
диференціали другого порядку (якщо для функцій
z f ( x1 , x2 ,..., xn ), qi ( x1 , x2 ,..., xn ) існують другі частинні
похідні і вони неперервні).
17

18. Метод множників Лагранжа

У загальнення достатньої умови існування
локального екстремуму для функції n змінних
приводить до такого правила: за функцією
Лагранжа виду (8) будується матриця Гессе, що має
блочну структуру розмірністю (m n) (m n) :
O P
H
P Q
18

19. Метод множників Лагранжа

де О – матриця розмірністю (m m) , що складається з
нульових елементів,
Р – матриця розмірністю ( m n) , елементи якої
визначаються так:
q1 ( x)
q1 ( x)
...
xn
x1
P ......
...
......
q m ( x)
q m ( x)
...
,
x1
xn
– транспонована матриця до Р розмірністю (n m) ,
Q – матриця розмірністю (n n) виду:
P
2 L( x, )
Q
xi x j , де i 1, m, j 1, n .
19

20. Метод множників Лагранжа

Розглянемо ознаки виду екстремуму розв’язку
системи (9). Нехай стаціонарна точка має
координати X ( x1 , x2 ,..., xn ) і ( 1 , 2 ,..., m ) .
1. Точка X є точкою максимуму, якщо,
починаючи з головного мінору порядку (m+1),
наступні (n–m) головних мінорів матриці Н
утворюють знакозмінний числовий ряд, знак
першого члена якого визначається множником
( 1) m 1 .
2. Точка X є точкою мінімуму, якщо, починаючи
з головного мінору порядку (m+1), знак наступних
(n–m) головних мінорів матриці Н визначається
m
20
множником ( 1) .

21. Приклад

Акціонерне
товариство
з
обмеженою
відповідальністю виділило 1200 Га ріллі під основні
сільськогосподарські культури – озиму пшеницю і
цукрові буряки. У табл. 1 маємо техніко-економічні
показники вирощування цих культур:
Необхідно знайти оптимальні площі
озимої пшениці та цукрових буряків.
посіву
21

22. Приклад

Нехай: х1 – площа ріллі під озимою пшеницею,
сотні Га;
х2 – площа ріллі під цукровими буряками, сотні
Га.
Звернемо увагу на те, що собівартість тонни
пшениці та цукрових буряків залежить від
відповідної площі посіву.
22

23. Приклад

Запишемо економіко-математичну модель цієї
задачі.
Критерієм оптимальності візьмемо максимізацію
чистого доходу:
max f 4(800 12,5 x12 200 x1 1200) x1100
35(300 12,5 x22 150 x2 650) x2 100
400( 12,5 x13 200 x12 400 x1 ) 3500( 12,5 x23 150 x22 350 x2 )
за умов:
x1 x 2 12.
23

24. Приклад

Запишемо функцію Лагранжа:
L( x1 , x2 , 1 ) 400( 12,5 x13 200 x12 400 x1 ) 3500( 12,5 x23 150 x22 350 x2 )
1 (12 x1 x2 ).
Візьмемо частинні похідні і прирівняємо їх до
нуля:
L
2
400
37
,
5
x
1 400 x1 400 1 0,
x1
L
2
3500
37
,
5
x
2 300 x1 350 1 0,
x2
L
12 x1 x2 0.
1
24

25. Приклад

З цієї системи рівнянь визначаємо координати
сідлових точок. З першого та другого рівняння
знаходимо 1 і, прирівнюючи вирази, маємо:
400( 37,5 x12 400 x1 400) 3500( 37,5 x 22 300 x2 350)
(10)
або, скоротивши на 100 обидві частини і розкривши
дужки, отримаємо:
150 x12 1600 x1 1600 1312,5 x22 10 500 x2 12 250 .
(11)
Із останнього рівняння системи маємо: x1 12 x2 .
25

26. Приклад

Підставимо
Отримаємо:
вираз для
x1
у
рівність
(11).
150 12 x2 1600 12 x2 1600 1312,5 x22 10 500 x2 12 250
2
або
150 144 24 x2 x22 19 200 1600 x2 1600
1312,5 x22 10 500 x2 12 250 ;
21 600 3600 x2 150 x22 19 200 1600 x 2 1600
1312,5 x22 10 500 x2 12 250 0.
26

27. Приклад

Отже, 1162 x2 8500 x2 11 450 0 ;
D 72 250 000 53 219 600 19 030 400
2
D 4362 .
8500 4362
5,53
2324
8500 4362
1,78
2324
x2(1)
(553 Га);
x2( 2)
(178 Га).
Відповідно дістаємо:
x1(1) 6,47 (647 Га);
x1( 2) 10,22 (1022 Га).
27

28. Приклад

Тобто отримали дві сідлові точки:
x1(1) 6,47;
(1)
x2 5,53.
x1( 2 ) 10,22;
( 2)
x2 1,78.
Перевіримо за допомогою достатньої умови
існування екстремуму спочатку сідлову точку
X 1 ( x1(1) ; x 2(1) ) .
Матриця Гессе має такий вигляд:
1
1
0
H 1 34100
0
1
.
0
401
625
28

29. Приклад

За вищезазначеним правилом визначаємо головні
мінори, починаючи з 2-го порядку ( m 1 1 1 2 ):
2
0
1 34100
0
1
3 1 34100
1
1
0
1
1
0
401625
,
435725
.
Отже, головні мінори утворюють знакозмінний
ряд та, починаючи з головного мінору 2-го порядку,
m 1
2
(
1
)
(
1
)
наступний мінор визначається знаком
,
(1) (1)
X
(
x
тобто 1
1 ;x2 ) є точкою максимуму.
29

30. Приклад

Обчислимо значення цільової функції в цій
точці:
f ( x1 6,47; x2 5,53) 4(800 532,26 1294 1200)647
35(300 382,26 829,5 650)553 4625863.
Аналогічні
обчислення
для
точки
X 1 ( x1( 2) 10,22; x2( 2) 1,78) показують, що вона не є
екстремальною.
Отже, цільова функція набуде максимального
значення, якщо озима пшениця вирощуватиметься
на площі 647 Га, а цукрові буряки – на площі 553 Га.
30

31. Узагальнений метод множників Лагранжа

Розглянемо таку задачу в загальному вигляді:
max (min) F f ( x1 , x2 ,..., x n ) ,
qi ( x1 , x2 ,..., xn ) bi (i 1,2,..., k );
qi ( x1 , x2 ,..., xn ) bi (i k 1,..., l );
q ( x , x ,..., x ) b (i l 1,2,..., m),
n
i
i 1 2
причому всі функції, що входять у задачу, мають
бути диференційовними хоча б один раз.
31

32. Узагальнений метод множників Лагранжа

Очевидно, що введення в ліві частини
нерівностей системи обмежень задачі додаткових
невід’ємних змінних xn i 0 (i k 1,..., m ) перетворює
початкову задачу в таку, що містить лише
обмеження-рівності, тобто яка за формою та
методом розв’язування збігатиметься з задачею (6)(7).
32

33. Необхідні умови існування сідлової точки

Для розроблення методів розв’язування окремих
типів задач нелінійного програмування важливе
значення має поняття сідлової точки, а також
визначення необхідних і достатніх умов існування
сідлових точок функції Лагранжа L( X , ) у
(n+m)-вимірному
просторі
змінних
( x1 , x2 ,..., xn , 1 , 2 ,..., m ) за довільних умов, які
можуть накладатися на їх знаки.
33

34. Необхідні умови існування сідлової точки

Розглянемо нелінійну задачу:
max F f ( x1 , x1 ,..., xn ) ,
qi ( x1 , x2 ,..., xn ) bi (i 1, m) .
Причому на компоненти векторів X , накладено
обмеження на знаки. Позначимо множину точок,
що задовольняють такі обмеження, через .
Функція Лагранжа для цієї задачі має вигляд:
m
L( X , ) = f ( x1 , x2 ,..., xn ) i (bi qi ( x1 , x2 ,..., xn )) .(12)
i 1
34

35. Необхідні умови існування сідлової точки

( X , ) ( x1 , x2 ,..., xn , 1 , 2 ,..., m )
Точка
називається
сідловою точкою функції Лагранжа (12), якщо для
всіх X , виконується співвідношення:
L( X , ) L( X , ) L( X , ) .
(13)
Для диференційовних функцій f ( X ) та qi ( X )
знайдемо необхідні умови існування сідлової точки.
(
X
,
)
(
x
,
x
,...,
x
,
,
,...,
Сідлова точка
1
2
n
1
2
m)
функції L( X , ) виду (12) за означенням задовольняє
умову:
L( X , ) L( X , ) .
35

36. Необхідні умови існування сідлової точки

Нерівність виконується для всіх точок Х, тобто
також і для тих, у яких лише одна координата
відрізняється від Х*. Допустимо, що це хk, а всі інші
збігаються з координатами сідлової точки
x j x j ( j 1,2,..., k 1, k 1,..., n) .
Оскільки права частина нерівності є фіксованою,
а в лівій частині змінюється лише одна координата
хk, то приходимо до функції однієї змінної
L( X , ) L( xk ) , яку можна зобразити графічно на
координатній площині.
36

37. Необхідні умови існування сідлової точки

Розглянемо спочатку випадок, коли xk 0 , тобто
лише частину координатної площини, для якої
xk 0 .
Можливі такі випадки:
1) коли всі x j 0 , то максимальне значення
функції L(xk) досягатиметься в точці, для якої
L( X , )
0
.
xk
37

38. Необхідні умови існування сідлової точки

2) коли максимум функції L(xk) досягатиметься в
точці xk 0 і розглядувана частинна похідна також
дорівнюватиме нулю:
L( X , )
0
.
xk
38

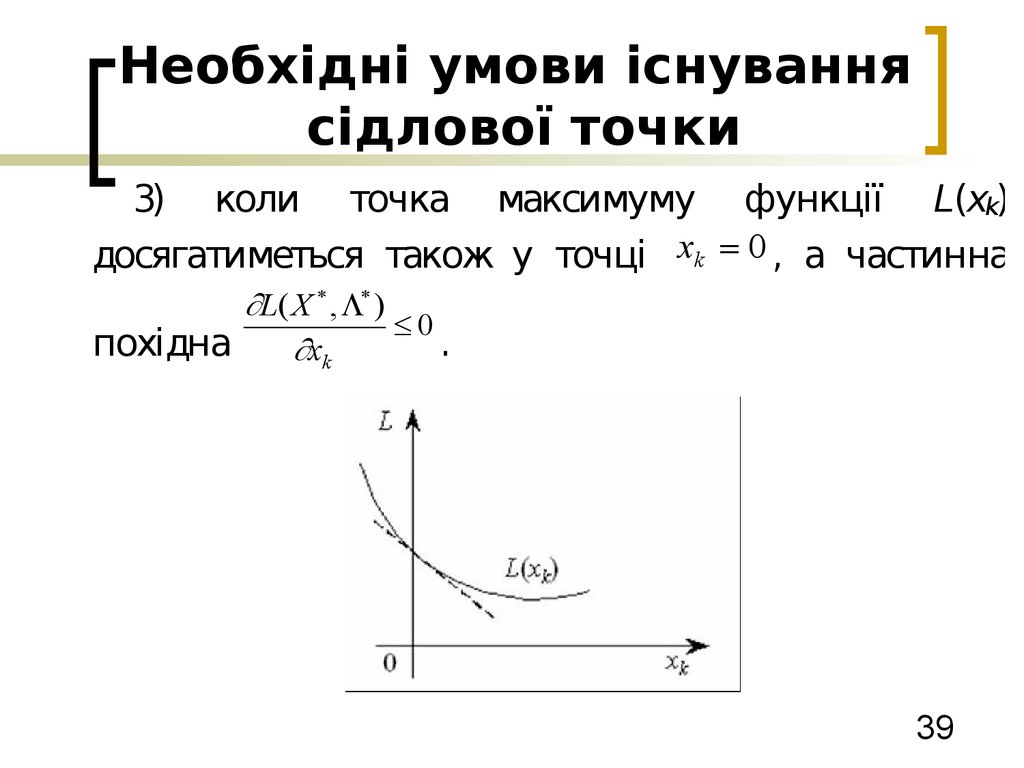
39. Необхідні умови існування сідлової точки

3) коли точка максимуму функції L(xk)
досягатиметься також у точці xk 0 , а частинна
L( X , )
0
похідна
.
xk
39

40. Необхідні умови існування сідлової точки

Узагальнюючи всі три ситуації, маємо:
L ( X , )
0
xj
L( X , )
x (x j ) 0 .
j 1
j
n
для x j 0 та
Розглядаючи другу частину нерівності (13):
L( X , ) L( X , )
аналогічними міркуваннями, що проілюстровані
на рис., встановлюються необхідні умови для
похідних по l функції Лагранжа в сідловій точці.
40

41. Необхідні умови існування сідлової точки

Об’єднуючи всі три випадки для невід’ємних
координат, маємо необхідні умови сідлової точки:
L( X , )
0
для тих індексів j, де x j 0 . (14)
xj
Зауважимо, що для xk 0 маємо ті самі випадки,
які зображено на відповідних рисунках, причому
графіки будуть симетрично відображені відносно
осі Оy, тобто для недодатних координат необхідна
умова має вигляд:
L( X , )
0
для тих індексів j, де x j 0 . (15)
xj
41

42. Необхідні умови існування сідлової точки

І нарешті, якщо на знак хj умови
накладаються, то необхідною умовою є:
L( X , )
0
xj
У загальнення
рівняння:
всіх
,
не
xj
– довільного знака. (16)
випадків приводить до
L( X , )
xj 0
xj
.
(17)
42

43. Необхідні умови існування сідлової точки

Розглядаючи другу частину нерівності (13), за
допомогою аналогічних міркувань встановлюємо
необхідні умови для похідних по i функції
Лагранжа в сідловій точці:
L ( X , )
0
i
L( X , )
0
i
для тих індексів і, де i 0 ,
для тих індексів і, де i 0 ,
(18)
(19)
L( X , )
0
для тих і, де i має довільний знак. (20)
i
43

44. Необхідні умови існування сідлової точки

Отже, справджується рівняння:
L( X , )
i 0
.
i
(21)
Сукупність співвідношень (14)-(21) становить
необхідні умови, які має задовольняти сідлова точка
( X , ) функції Лагранжа для точок, що належать
L
(
X
,
) повинна мати
множині . При цьому
частинні похідні по всіх компонентах векторів X , .
44

45. Список літератури

Основна:
1. Зайченко Ю. П. Дослідження операцій :
підручник / Ю. П. Зайченко. – К. : ВІПОЛ, 2000.
2. Таха Х. Введение в исследование операций /
Х. Таха. – М. : Вильямс, 2001.
3. Ульянченко О. В. Дослідження операцій в
економіці / О. В. Ульянченко. – Х. : Гриф, 2003.
Додаткова:
1.
Вітлінський В. В.
Математичне
програмування
/
В. В. Вітлінський,
С. І. Наконечний, Т. О. Терещенко. – К., 2001.
2.
Кузнецов А. В.
Математическое
программирование / А. В. Кузнецов и др. – М.:
Высшая школа, 1994.
45