Похожие презентации:
Уравнения и неравенства с параметрами
1. Уравнения и неравенства с параметрами
Линейные уравнения2. Уравнение вида Ах=В, где А, В – выражения, зависящие от параметров, а х- неизвестное, называется линейным уравнением с параметрами.
Уравнение вида Ах=В, где А, В – выражения,зависящие от параметров, а х- неизвестное,
называется линейным уравнением с
параметрами.
Решить уравнение с параметрами – значит для всех значений параметров
найти множество всех корней заданного уравнения.
Линейное уравнение исследуется по следующей схеме:
1.
Если А=0, то имеем уравнение 0·х=В. Тогда, если, кроме того, В≠0,
то уравнение не имеет решений, а если В=0, то уравнение имеет вид
0 ·х=0 и удовлетворяется при любом х, т. е. решением уравнения
будет множество всех действительных чисел.
2.
Если А≠0, то уравнение имеет единственное решение х=В/А.
Замечание. Если линейное уравнение или уравнение, сводящееся в
линейному, не представлено в виде Ах=В, то сначала нужно
привести его к стандартному виду и только после этого проводить
исследование.
Если для каких – нибудь значений параметров уравнение не имеет
смысла, то для этих значений параметров оно не имеет решений.
Кроме этого, уравнение может не иметь решений и при других
значениях параметров.
3.
Пример1. Для всех значений параметра kрешить уравнение k 4 x 2k 1
Уравнение уже записано в стандартном виде, поэтому проведем
его исследование по указанной выше схеме.
1. Если k+4=0, т. е. k= -4, то уравнение имеет вид 0 ·х= -7. Это
равенство ни при каком х не выполняется, поэтому уравнение
не имеет решений: хЄǾ.
2. Если k+4≠0, т. е. k≠-4, то обе части уравнения можно делить на
k+4.
Тогда х 2k 1.
k 4
Ответ : если k 4, то х ;
если k 4, то х 2k 1.
k 4
4.
Пример2. Для всех значений параметра арешить уравнение
3
а 1
4
x 3а 4 0
Запишем уравнение в стандартном виде
3 а 1 x 3а 4 0
4
Схема исследования.
1) 3 а 1 0 а 4 . Тогда уравнение имеет вид 0 х 0.
3
4
Это равенство верно при любом х. Следовательно, решением уравнения
будет все множество действительных чисел : х R.
2) 3 а 1 0 а 4 . Тогда х 4 3а 4.
3
3
4
а 1
4
Ответ : если а 4 , то х R
3
если а 4 , то х 4.
3
5.
Пример3. Для всех значений параметра pрешить уравнение p2 1 x p3 1.
1)p2 1 0 p 1.
При p 1 уравнение имеет вид 0 х 2. Следовательно, х .
При p 1 уравнение имеет вид 0 х 0. Следовательно, х R.
2 p 1
p
1
p
3
2 p 1
p
1
p
2
2)p 1 0 p 1. Тогда х
.
p 1
p 1 p 1
p2 1
Ответ : если p 1, то х ; если p 1, то х R;
2 p 1
p
если p 1, то х
.
p 1
6.
Пример 4. При каких значениях параметра а уравнениеа 1 2а имеет положительные решения.
х а а 2
Если а 2, то х .
Если а 2, то уравнение равносильно системе
2а х а а 1 а 2 , 2ах 3а2 а 2,
х а 0
х а.
1)Если а 0,то имеем 0 х 2 х .
2 а 2
3
а
2)Если а 0 и а 2 ,то х
.
2а
Найдем значения параметра а, при которых х а. Имеем :
3а2 а 2 а а2 а 2 0, а 1,
2а
а
0
а 2.
Таким образом, если а 10
; ;2 ,то исходноеуравнение не имеет решения;
2 а 2
3
а
если а 10
; ;2 ,то оно имеет единственное решение х
.
2а
Это решение будет положительным, если параметр а удовлетворяет неравенству
2
3
а
1
а
3а2 а 2 0
3 0.
2а
2а
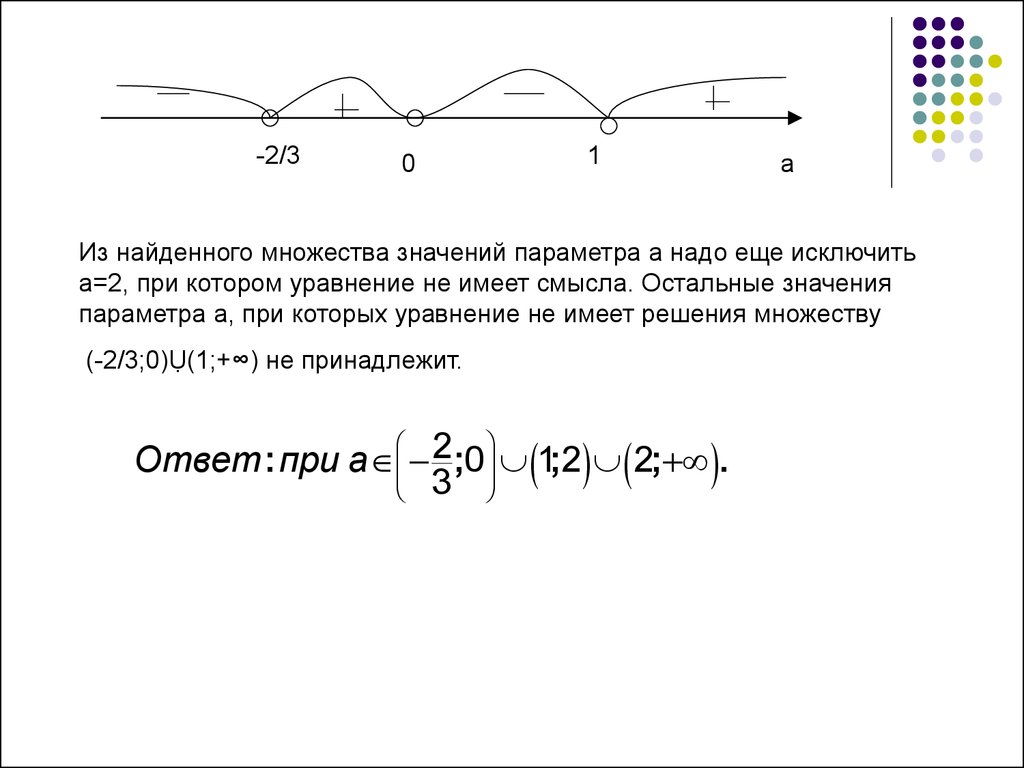
Решим полученное неравенство методом интервалов :
7.
-2/30
1
а
Из найденного множества значений параметра а надо еще исключить
а=2, при котором уравнение не имеет смысла. Остальные значения
параметра а, при которых уравнение не имеет решения множеству
(-2/3;0)Ụ(1;+∞) не принадлежит.
2
Ответ : при а ;0 12
; 2; .
3
8.
Пример 5. При каких значениях параметров а и b уравнение2a b x a b 1 не имеет решений.
В данном случае необходимо и достаточно, чтобы
2a b 0,
b 2a,
b 2a,
a b 1 0 a 2b 1 0 a 1
или,что равносильно,
a b / 2,
a b / 2,
b / 2 1
b 2.
Ответ : при a 1, b 2a или a b / 2, b 2
9. Уравнения и неравенства с параметрами
Квадратные уравнения10. Уравнение вида Ах2 +Вх+С=0, где А, В,С – выражения, зависящие от параметров, а х- неизвестное, называется квадратным уравнением с параметрами.
Уравнение вида Ах2 +Вх+С=0, где А, В,С –выражения, зависящие от параметров, а хнеизвестное, называется квадратным
уравнением с параметрами.
В множестве действительных чисел это уравнение
исследуется по следующей схеме.
1.
Если А=0, то имеем линейное уравнение Вх+С=0.
2.
Если А≠0 и дискриминант уравнения D=В 2 -4АС<0,
то уравнение не имеет действительных решений.
3.
Если, А≠0 и D=0, то уравнение имеет единственное
решение х=-В/2А или, как ещё говорят,
совпадающие корни х1= х2
=-В/2А.
4. Если А≠0 и D>0, то уравнение имеет два различных
корня
х В D
12
,
2A
11.
Пример 6. Найти все значения параметра а, для которых квадратноеуравнение a 1 x2 2 2а 1 х 4а 3 0
а)имеет два различныхкорня;б )не имеет корней; в)имеет один корень.
Данное уравнение по условию является квадратным, поэтому
а 1 0 а 1. Рассмотрим дискриминант уравнения
2
D 4 2a 1 4 a 1 4a 3 4 5a 4
Согласно схеме исследования, имеем :
4
D 0, 4 5a 4 0, a ,
а)
5
a
1
a
1
a 1
4
D 0, a ,
4
б)
5 a ;
a 1
5
a 1
4
D 0, a ,
4
в)
5 a .
a 1
5
a 1
Ответ : если a 4 и а 1,то уравнение имеет два различных корня;
5
если a 4 ,то оно не имеет корней;
5
если a 4 ,то оно имеет один корень.
5
12.
Пример 7. При каких значениях параметра ауравнение a 6 x2 2ах 1 0 имеет единственное решение.
По условию задачи уравнение необязательно является
квадратным, поэтому надо рассмотреть два случая.
1)а 6 0 а 6. При этом получаем линейное уравнение
12х 1 0, которое имеет единственное решение.
Это решение по условию задачи необязательно находить.
2)а 6. В этом случае уравнение является квадратным и
имеет единственное решение,
если дискриминант D 4a2 4(a 6) 4(a2 a 6)
равен нулю, т.е. а2 а 6 0 а 3, а 2
1
2
Ответ : приа 6; 2;3
13.
Пример 8. При каких значениях параметра ауравнение a2 а 2 x2 (а 1)х 1 0 не имеет решений.
Снова надо рассмотреть два случая.
1)а2 а 2 0 а 2, а 1 .
1
2
При а 2 получаем линейное уравнение 3х 1 0,
которое имеет решение.
При а 1 уравнение имеет вид 0 х 2 0 х 1 0,
поэтому не имеет решений.
2)а2 а 2 0 а 2, а 1. В данном случае уравнение
1
2
является квадратным и оно не имеет решений ,
если дискриминант D (a 1)2 4(a2 а 2) 3a2 6a 9
3 а 3 а 1 отрицателен, т. е.
D 0 3 а 3 а 1 0 а 3 а 1 0 а ; 1 3; .
Теперь с учетом первого случая получаем
Ответ : при а ; 1 3; .
14.
Пример 9. При каких значениях параметров а и bуравнение a2 а 6 x 2 (а b 4)х a2 4a 3 0
имеет не менее трех различных решений.
Если квадратное или линейное уравнение имеет более двух
различных решений , то оно обязательно имеет бесконечное
множество решений, совпадающее с R.
Это возможно тогда и только тогда, когда уравнение имеет вид
0 х2 0 х 0 0,т.е.
а2 а 6 0
a 2,a 3
2
1
a 3
a
b
4
0
b
a
4
2
a 1,a 3 b 1
4
а 4а 3 0 3
Ответ : при а 3, b 1.
15.
Пример 10. Для всех значений параметра арешить уравнение а 1 x 2 2ах a 2 0
1)а 1 0 а 1. Уравнение имеет вид 2х 3 0 х 3
2
2)а 1. Найдем дискриминант уравнения D 4а2 4 а 1 а 2 4а 8.
В зависимости от значения D возможны случаи.
D 0 4a 8 0 a 2,
а)
a 2. Уравнение не имеет решений , т.е. х .
a
1
a
1
a
1
D 0 4a 8 0
б)
a 2. Тогда х а 2 2.
а 1 2 1
a 1
a 1
D 0 4a 8 0 a 2,
в)
Уравнение имеет два различных корня х 2а 4а 8 а 2 а .
12
,
2(а 1)
а 1
a 1
a 1
a 1
Ответ : если а 1, то х 2;
3
если а 2, то х 2;
если а 2, то х ;
если а 2 и а 1, то х1,2 а 2 а .
а 1
16. Уравнения и неравенства с параметрами
Квадратные уравнения.Теорема Виета.
17. При решении многих задач, связанных с квадратными уравнениями, содержащими параметры, используются следующие теоремы.
При решении многих задач, связанных сквадратными уравнениями, содержащими
параметры, используются следующие теоремы.
Теорема Виета.
Если х х корни квадратного уравнения Ах 2 Вх С 0,А 0,то
1, 2
В
х х ,
1
2
А
С.
х х
А
1 2
Теорема 1.
Для того, чтобы корни квадратного трехчлена Ах 2 Вх С
были действительны и имели одинаковые знаки, необходимо
и достаточно выполнение следующих условий :
D B2 4AC 0, x x C 0
1 2 A
При этом оба корня будут положительными, если x x В 0,
1 2
A
и оба отрицательны, если x x В 0.
1 2
A
18. При решении многих задач, связанных с квадратными уравнениями, содержащими параметры, используются следующие теоремы.
Теорема 2.Для того, чтобы корни квадратного трехчлена Ах 2 Вх С
были действительны и оба неотрицателы или оба неположительны,
необходимо и достаточно выполнение следующих условий :
D B2 4AC 0, x x C 0
1 2 A
При этом оба корня будут неотрицательны, если x x В 0,
1 2
A
и оба корня будут неположительны, если x x В 0.
1 2
A
Теорема 3.
Для того, чтобы корни квадратного трехчлена Ах 2 Вх С
были действительны и имели разные знаки,
необходимо и достаточно выполнение условия :
x x C 0
1 2 A
При этом условие D B2 4AC 0 выполняется автоматически.
19.
Пример 11. При каких значениях параметра ауравнение x2 2(а 1)х a2 0 имеет действительные корни
сумма квадратов которых равна 4.
По условию уравнение должно иметь действительные корни,т.е.
D 0, и х 2 х 2 4, где х , х корни уравнения.
1 2
1 2
Значит,
D 0
2
D
4
а
1
4а2 8а 4,
2 2
х1 х2 4
2
х 2 х 2 (х х )2 2х х 4 а 1 2а2 2а2 8а 4
1 2
1 2
12
так как по теореме Виета х х 2 а 1 х х а2
1 2
12
1
a
1
8а 4 0
2
a 2
2
а 4
2а 8а 4 4 2а2 8а 0
а 0
отсюда а 0.
Ответ : при а 0
20.
Пример 12. При каких значениях параметра mуравнение x 2 mх 20m 0 имеет действительные корни
отличающиеся друг от друга на 9.
По условию D 0 и х х 9 или х 2 х 9,т.е. х1 х2 9 х1 х2 81
1 2
1
2
х1 х2 4 х1х2 81
Так как D m2 80m, а по формулам Виета х1 х2 m, х1х2 20m,
то имеем
m2 80m 0
m2 80m 81 m 81 m 1
1
2
m2 80m 81
Ответ : при m 811
; .
21. Уравнения и неравенства с параметрами
Квадратные неравенства.22. Неравенства видов Ах2 +Вх+С>0 (≥0), Ах2 +Вх+С<0 (≤0) где А, В,С – выражения, зависящие от параметров, A≠0? а х- неизвестное, называются квадратным не
Неравенства видов Ах2 +Вх+С>0 (≥0), Ах2 +Вх+С<0 (≤0)где А, В,С – выражения, зависящие от параметров, A≠0?
а х- неизвестное, называются квадратным
неравенствами с параметрами.
Неравенство Ах2 +Вх+С>0 исследуется по следующей
схеме.
1.
Если А=0, то имеем линейное неравенство Вх+С>0.
2.
Если А≠0 и дискриминант D>0, то разлагая
квадратный трехчлен на множители, получим
неравенство А(х-х1)(х-х2)>0, где х1,х2-корни
уравнения Ах2 +Вх+С=0.
3.
Если, А≠0 и D=0, то имеем неравенство А(х-х1)2>0.
4.
Если А≠0 и D<0, то при A>0решением будет все
множество действительных чисел R; при А<0
неравенство решений не имеет.
Остальные неравенства исследуются аналогично
23.
Часто при решении квадратных неравенств используютсяследующие свойства квадратного трехчлена Ах2 +Вх+С:
1.
Если A>0 и D<0, то Ах2 +Вх+С>0 при всех х;
2.
Если A<0 и D<0, то Ах2 +Вх+С<0 при всех х.
При решении многих задач, связанных с квадратичной
функцией f(x)= Ах2 +Вх+С, А≠0, в частности, при решении
квадратных неравенств удобно использовать
схематическое изображение графика функции y=f(x)параболы, которая в зависимости от коэффициента А и
дискриминанта D имеет следующие расположения
относительно оси абсцисс.
A>0
D<0
A>0
D=0
A>0
D>0
x1
xв
A<0
D<0
A<0
D=0
xв
A<0
D>0
x1
x2
x2
24.
Пример 13. Для всех значений параметра pнеравенство x2 2(p 1)х p2 0.
Найдем дискриминант
D 4(p 1)2 4p2 8p 4 4 2p 1 .
Возможны случаи.
1)D 0,то есть 2p 1 0 p 1. Так как коэффициент при х 2,равный 1,
2
положителен,то неравенство выполняется при всех х,т. е. х R.
2)D 0 2p 1 0 p 1.
2
2
При этом неравенство имеет вид х 2 х 1 0 x 1 0 x ; 1 1; .
4
2
2 2
3)D 0 2p 1 0 p 1.Тогда квадратный трехчлен, расположенный в левой части
2
неравенства, имеет корни
х p 1 2p 1, х p 1 2p 1,
1
2
причем х x . Разлагая этот трехчлен на множители, имеем :
1 2
х х х х 0, откуда методом интервалов находим :
1
2
25.
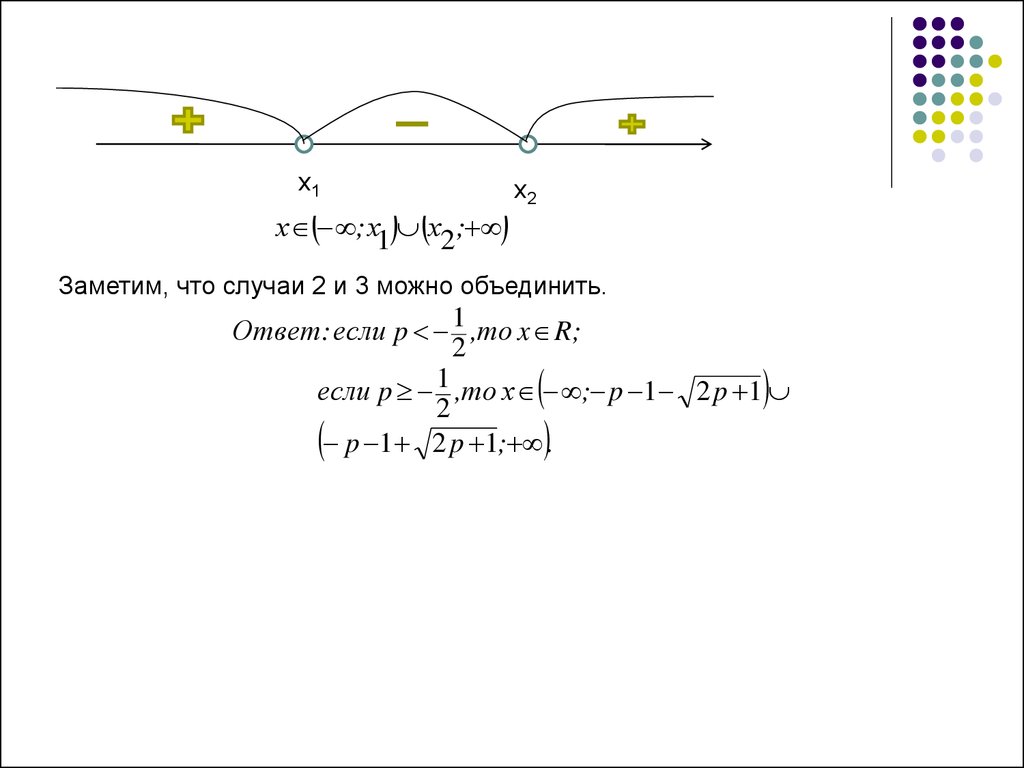
x1х ; х1 х2 ;
x2
Заметим, что случаи 2 и 3 можно объединить.
Ответ: если p 1 ,то x R;
2
если p 1 ,то х ; p 1 2 p 1
2
p 1 2 p 1; .























 Математика
Математика








