Похожие презентации:
Моделирование технологических процессов. Математические модели микроуровня
1. Моделирование технологических процессов
Математические модели микроуровня1
2. Уравнения эллиптического типа
Закон сохранения массы жидкости в выделенном объеме VС силу произвольного выбора объема V подынтегральная
функция должна быть тождественна равна нулю и следует
уравнение неразрывности сплошной среды:
2
3. Уравнения эллиптического типа
Для несжимаемой жидкости плотность является постоянной :Рассмотрим установившееся
течение жидкости, для которого ее
скорость не зависит от времени:
3
4. Уравнения эллиптического типа
Для безвихревое теченияжидкости, существует
потенциал скоростей:
Свойства потенциала скоростей:
градиент потенциала скоростей
определяет скорость жидкости:
4
5. Уравнения эллиптического типа
Для потенциала скоростей,справедливо уравнение Лапласа:
Laplace, Pierre-Simon
(1749–1827), французский
математик, физик и
астроном
или
здесь
оператор Лапласа
Уравнение Лапласа возникает во многих
физических задачах механики,
теплопроводности, электростатики, гидравлики,
квантовой физике, в частности в уравнении
Шрёдингера.
5
6. Уравнения эллиптического типа
Электрическое поле в среде сдиэлектрической проницаемостью
характеризуется напряженностью поля
и по теореме Гаусса для электрического
поля:
Johann Carl Friedrich Gauß;
1777-1855, Гёттинген):
немецкий математик,
механик, физик, астроном
и геодезист.
где
– диэлектрическая
постоянная; – объемная
плотность электрических
зарядов; V – некоторый объем
пространства, ограниченный
замкнутой поверхностью S
6
7. Уравнения эллиптического типа
С помощью теоремыОстроградского-Гаусса
преобразуем последнее
выражение к дифференциальной
форме:
или
7
8. Уравнения эллиптического типа
В силу произвольного
выбора объема V
подынтегральная функция
должна быть тождественна
нулю!
Связь электрического
поля и
электростатического
потенциала:
здесь
оператор Лапласа
8
9. Уравнения эллиптического типа
Для электростатического потенциаласправедливо уравнение Пуассона:
Siméon Denis Poisson
(1781-1840, Франция),
французский математик,
механик и физик.
В декартовой системе координат:
Уравнение Пуассона описывает:
• электростатическое поле,
• стационарное поле температуры,
• поле давления,
• поле потенциала скорости в гидродинамике.
9
10. Краевые задачи для уравнений эллиптического типа
В каждой задачи, связанной с уравнениями Лапласа и Пуассона,искомое решение должно:
1) удовлетворять
уравнению в области
2) удовлетворять некоторому
дополнительному условию на
границе этой области.
10
11. Краевые задачи для уравнений эллиптического типа
В зависимости от вида граничных условий различают следующиевиды граничных задач:
1) Задача Дирихле
здесь S – поверхность ограничивающая область решений;
– точка принадлежащая границе области S.
11
12. Краевые задачи для уравнений эллиптического типа
В зависимости от вида граничных условий различают следующиевиды граничных задач:
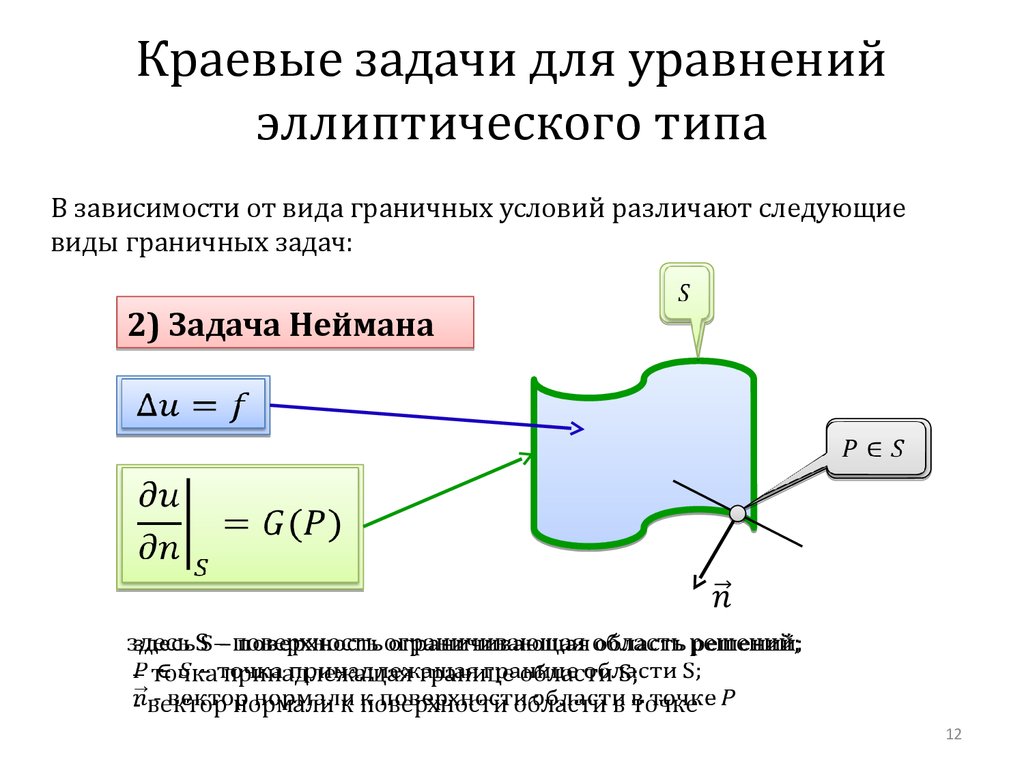
2) Задача Неймана
здесь
S – поверхность ограничивающая область решений;
– точка принадлежащая границе области S;
- вектор нормали к поверхности области в точке
12
13. Краевые задачи для уравнений эллиптического типа
В зависимости от вида граничных условий различают следующиевиды граничных задач:
3) Смешанная задача
здесь
S – поверхность ограничивающая область решений;
– точка принадлежащая границе области S;
- вектор нормали к поверхности области в точке
13
14. Уравнения параболического типа
Процесс передачи теплоты от болеенагретых частей тела к менее нагретым
связан с изменением температуры T в
различных частях рассматриваемой
области пространства.
Поэтому описание процесса
теплопереноса в
макроскопической теории в
общем случае сводится к
определению
нестационарного
температурного поля в
рассматриваемой области
пространства.
14
15. Уравнения параболического типа
Рассмотрим одномерный процесс передачи(1)
теплоты теплопроводностью в плоском слое
изотропного материала, считая, что
температура является функцией лишь одного
пространственного переменного .
0
Плотность материала, его
(2)
удельную массовую теплоемкость и
коэффициент теплопроводности в
общем случае неоднородной среды
будем считать также зависящими
только от одной пространственной
координаты .
(3) Среда неподвижна , а изменение объема
материала, связанное с изменением
температуры, пренебрежимо мало, поэтому
можно считать, что процесс теплопроводности
не связан с совершением механической
работы.
15
16. Уравнения параболического типа
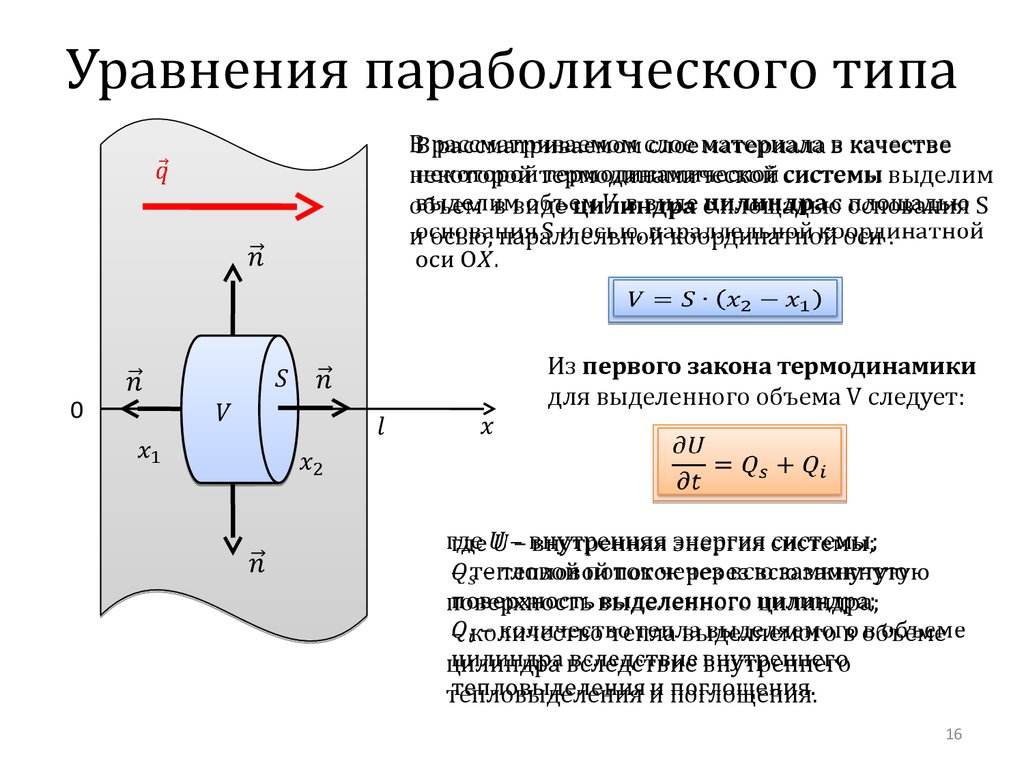
рассматриваемом слое материала в качествеВ
некоторой термодинамической системы выделим
объем в виде цилиндра с площадью основания S
и осью, параллельной координатной оси .
0
Из первого закона термодинамики
для выделенного объема V следует:
U – внутренняя энергия системы;
где
– тепловой поток через всю замкнутую
поверхность выделенного цилиндра;
– количество тепла выделяемого в объеме
цилиндра вследствие внутреннего
тепловыделения и поглощения.
16
17. Уравнения параболического типа
Внутренняя
энергия цилиндра может быть
найдена интегрированием объемной плотности
внутренней энергии по его объему :
0
Изменение объемной плотности
энергии может наблюдаться только
вдоль оси цилиндра (ось ОХ)
17
18. Уравнения параболического типа
Поэтому изменение внутренней энергиицилиндра U за единицу времени (скорость
изменения внутренней энергии):
0
Тепловое
расширение среды
отсутствует, поэтому геометрические
размеры цилиндра не изменяются с
течением времени: площадь основания
цилиндра S и его высота
18
19. Уравнения параболического типа
Тепловой
поток можно найти с помощью
интегрирования по поверхности (граница
раздела выделенного объема) нормальную
составляющую плотности теплового потока:
0
- плотность теплового потока.
Площадь граница раздела
выделенного объема (площадь
поверхности выделенного
цилиндра)
19
20. Уравнения параболического типа
Согласно закону Фурье, при передачетеплоты теплопроводностью
плотность потока тепла составляет:
0
рассматриваемом случае вектор теплового
В
потока имеет лишь одну составляющую (вдоль
оси ОХ)
Jean Baptiste Joseph Fourier (1768-1830, Франция),
французский математик и физик.
20
21. Уравнения параболического типа
Тепловой поток через выделенный объемцилиндра отличен от нуля только в
направлении оси ОХ(т.е. поток проходит лишь
через основания цилиндра):
0
Вектора
нормали к боковой
поверхности цилиндра
перпендикулярны направлению
потока!
21
22. Уравнения параболического типа
На основании закона Фурье, тепловые потокичерез поверхность оснований цилиндра
составляют:
0
Следовательно, суммарный поток тепла через
полную поверхность цилиндра составляет:
22
23. Уравнения параболического типа
Рассмотрим тепловой поток вкачестве первообразной функции
0
Первообрáзной или примитии́вной
функцией данной функции f(x)
называют такую F(x), производная
которой (на всей области определения)
равна f, то есть
F'(x) = f(x). Вычисление первообразной
заключается в нахождении
неопределённого интеграла, а сам
процесс называется интегрированием
23
24. Уравнения параболического типа
Внутри выделенного объема вследствиепротекания эндо- или экзотермических
реакций, прохождения электрического
тока, испарения влаги в пористом
материале и других причин может
выделяться или поглощаться теплота
0
где
- объемная плотность (удельную
мощность) тепловых источников, т.е.
количества тепла которое выделяется
(F > 0) или поглощается (F < 0) за
единицу времени в единице объема.
24
25. Уравнения параболического типа
Внутри выделенного объема вследствиепротекания эндо- или экзотермических
реакций, прохождения электрического тока,
испарения влаги в пористом материале и
других причин может выделяться или
поглощаться теплота
0
В силу симметрии
задачи:
где
- удельную мощность тепловых
источников, т.е. количества тепла которое
выделяется (F > 0) или поглощается (F < 0) за
единицу времени в единице объема.
25
26. Уравнения параболического типа
Таким образом, из первого закона термодинамики (закон сохранения ипревращения энергии) следует:
Подстановка полученных выше соотношений дает:
26
27. Уравнения параболического типа
силу произвольности выбора координат иВ
оснований цилиндра равенство нулю интеграла
возможно лишь при равенстве нулю
подынтегральной функции:
0
Таким образом, в описываемом
процессе передачи теплоты должно
выполняться дифференциальное
соотношение:
27
28. Уравнения параболического типа
Удельная массовая теплоемкостьматериала:
0
где Q – количество
теплоты необходимое для
изменения температуры
тела на 1 градус
Количество теплоты
переданное системе с
объемной плотностью
внутренней энергии
рассматриваемой среды
в общем случае
неоднородной среды
может зависеть от
пространственной
координаты
28
29. Уравнения параболического типа
Установим связь между изменениемудельной внутренней энергии и
изменением температуры:
0
Изменение
удельной внутренней
энергии рассматриваемого объекта
(цилиндра) за единицу времени
связано с изменением температуры
объекта:
29
30. Уравнения параболического типа
Таким образом, одномерный процессраспространения теплоты описывается
уравнением:
0
30
31. Уравнения параболического типа
Для однородного материала снезависящими от температуры
теплофизическими характеристиками
и уравнение можно записать в виде:
0
приведенный
коэффициент
теплопроводности
скорость изменения
температуры в
системе
31
32. Уравнения параболического типа
Полученное уравнение является дифференциальными уравнениемв частных производных параболического типа
Эти уравнения лежат в основе
математических моделей, описывающих:
• процесс передачи теплоты в
неоднородных и однородных телах;
• диффузионный процесс переноса массы
и диффузия частиц (например,
нейтронов) в веществе;
• процессы конвекции;
• процессы движения жидкостей и газов.
32
33. Уравнения параболического типа. Начальные и граничные условия
Чтобы с помощьюуравнения
параболического типа
можно было описать
эволюцию, необходимо
знать распределение
температуры в
начальный момент
времени, т.е. задать
начальное условие.
Для рассматриваемого
одномерного процесса начальное
условие задается в виде
известной зависимости
температуры в начальный
момент времени t = 0:
33
34. Уравнения параболического типа. Начальное условие
Для рассматриваемого одномерного процесса переноса тепланачальное условие задается в виде известной зависимости
температуры в начальный момент времени t = 0:
34
35. Уравнения параболического типа. Граничные условия
Кроме того, требуется знать тепловой режим на поверхности тела,т.е. задать граничные условия во всех точках поверхности тела в
любой момент времени.
В одномерном процессе соответствующие граничные условия
задаются на граничных поверхностях слоя и
Граничные условия в
задачах
теплопроводности
могут быть заданы
различными
способами.
35
36. Уравнения параболического типа. Граничные условия
1) Граничное условие первого рода, когда в каждой точкеповерхности тела задают температуру
Здесь
– поверхность ограничивающая
область решений;
– точка принадлежащая границе
области S
36
37. Уравнения параболического типа. Граничные условия
2) Граничное условие второго рода, когда на поверхности телазадается тепловой поток:
Здесь
– вектор плотности теплового
потока;
- вектор нормали к поверхности
области в точке ;
– точка принадлежащая границе
области
– поверхность ограничивающая
область решений.
37
38. Уравнения параболического типа. Граничные условия
3) Граничное условие третьего рода описывает тепловой режимна поверхности тела, соответствующий конвективному
теплообмену по закону Ньютона с окружающей внешней средой,
имеющей температуру :
– коэффициент теплообмена
(теплоотдачи)
– вектор плотности теплового потока;
- вектор нормали к поверхности области
в точке ;
– точка принадлежащая границе области
тела.
38
39. Уравнения параболического типа. Граничные условия
4) При описании температурных полей в многослойныхструктурах и оболочках на поверхности контакта двух тел
используют граничные условия сопряжения (идеальный
тепловой контакт):
– вектор плотности теплового потока
в 1-ой среде;
– вектор плотности теплового потока
во 2-ой среде;
- вектор нормали к поверхности
Для
идеального
теплового
контакта
эти
условия
Для
идеального
теплового
контакта
эти
условия
области в точке ;
означают
равенство температур и тепловых
означают
– точка принадлежащая границе
области равенство температур и тепловых
потоков
потоковна
наконтактной
контактнойповерхности
поверхности
раздела двух тел.
39
40. Уравнения параболического типа. Граничные условия
5) Граничные условия для неидеального теплового контакта,т.е. когда теплообмен между частями тела затруднен и происходит
по закону конвекционного теплообмена (закон Ньютона):
теплообмена (теплоотдачи)
– коэффициент
Для
неидеального
теплового контакта, т.е. когда
– вектор плотности теплового потока
теплообмен
в 1-ой среде; между частями тела затруднен
температуры
на поверхности
частей системы не равны
– вектор плотности
теплового потока
между
во 2-ой собой
среде; , хотя имеет место равенство тепловых
потоков
.
- вектор нормали
к поверхности
области в точке разность
;
Возникающая
температур определяет
– точка принадлежащая
границе
областипо механизму
теплообмен
между частями
системы
разделаНьютона.
двух тел.
закона
40
41. Уравнения параболического типа. Граничные условия
6) Нелинейное граничное условие формулируется в случае еслиосновным механизмом теплообмена поверхности тела с
окружающей средой является излучение, то по закону Стефана Больцмана:
– степень черноты материала, которая в общем случае
зависит от температуры;
– постоянная Стефана – Больцмана;
– вектор плотности теплового потока;
- вектор нормали к поверхности
области в точке ;
– точка принадлежащая границе области
раздела двух тел.
41
42. Уравнения гиперболического типа
Рассмотрим процесс колебаний тонкой упругой нити (струны), котораяможет свободно изгибаться.
Выделим произвольный участок струны
который при колебаниях струны
деформируется в участок , длина дуги
которого в момент времени составляет:
Рассмотрим только малые
поперечные колебания струны,
считая, что перемещение частиц
струны происходит в одной
плоскости и все точки струны
движутся перпендикулярно оси ОX.
42
43. Уравнения гиперболического типа
Из предположения о малости колебаний следует, что длинавыделенного участка струны в любой момент времени:
Это
означает, что в процессе малых
колебаний удлинением участков
струны можно пренебречь.
В этом случае, согласно закону Гука,
натяжение в каждой точке струны
не будет изменяться.
Robert Hooke (1635-1703, Англия)
естествоиспытатель, учёный-энциклопедист, один
из отцов физики, в особенности экспериментальной.
43
44. Уравнения гиперболического типа
Для
поперечных колебаний струны сумма проекций на ось ОU сил натяжения ,
действующих на концах участка струны :
где
Воспользуемся
геометрическим смыслом
производной – «Производная в точке равна
угловому коэффициенту касательной к графику
функции в этой точке»
44
45. Уравнения гиперболического типа
Из предположения о малости колебаний следует:Таким образом, сумма проекций сил
натяжения на выделенный участок
струны:
Первообрáзной или примитии́вной
функцией данной функции называют
такую , производная которой (на всей
области определения) равна , то есть .
45
46. Уравнения гиперболического типа
Закон динамики поступательного движения(закон Ньютона), который для механической
системы:
здесь
- импульс системы, равный сумме
импульсов всех ее частиц;
- результирующая внешняя сила.
Sir Isaac Newton
(1643-1727, Англия).
Физик, математик,
механик и астроном,
один из создателей
классической физики.
качестве такой механической системы
В
рассмотрим выделенный участок струны
Учитывая, что движение этой системы происходит
в направлении, перпендикулярном оси ОX,
запишем закон Ньютона в проекции на ось ОU:
46
47. Уравнения гиперболического типа
Проекция импульса выделенного участка струны :- линейная плотность
распределения массы в
струне, которая в общем
случае изменяется вдоль
струны.
Sir Isaac Newton
(1643-1727, Англия).
Физик, математик,
механик и астроном,
один из создателей
классической физики.
Следовательно, скорость изменения импульса
выделенного участка струны :
47
48. Уравнения гиперболического типа
Проекция
внешних сил состоит из двух слагаемых: одно из них учитывает
действие сил натяжения на концах выделенного участка струны , а другое суммарную вынуждающую силу , действующую на частицы этого участка.
Таким образом, второй закон
Ньютона для участка струны
запишется в виде интегрального
соотношения:
48
49. Уравнения гиперболического типа
силу произвольности выбора отрезка из уравнения следует, что в любойВ
точке струны в любой момент времени подынтегральное выражение
должно обращаться в нуль, т.е.
Полученное
соотношение
представляет собой
дифференциальное уравнение в
частных производных второго
порядка относительно искомой
функции .
Оно описывает процесс малых
поперечных колебаний струны, и
его называют неоднородным
одномерным волновым уравнением,
или уравнением плоских волн.
49
50. Уравнения гиперболического типа. Задача Коши
Причинами, вызывающими
колебания струны, могут являться
начальные отклонения струны от
равновесного положения или
сообщенный струне начальный
импульс, обусловливающий
некоторое распределение скоростей
частиц струны.
Поэтому необходимо задать начальные условия:
50
51. Методы решения уравнений в частных производных. Метод Фурье
Метод разделения переменных, или методФурье, является одним из основных методов
решения задач математической физики в
ограниченных областях.
Jean Baptiste Joseph Fourier
(1768-1830, Франция),
французский математик и
физик.
Идея метода Фурье основана на линейности и
однородности уравнения и граничных условий.
В этом случае справедлив принцип
суперпозиции для любых частных решений и
уравнения, удовлетворяющих начальным и
граничным условиям, т.е. функция.
также удовлетворяет
уравнению и
граничным условиям
51
52. Методы решения уравнений в частных производных. Метод Фурье
Нетривиальное решение уравненияищется в виде произведения функций,
например:
Jean Baptiste Joseph Fourier
(1768-1830, Франция),
французский математик и
физик.
или
или
52


















































 Математика
Математика Физика
Физика








