Арифметическая и геометрическая прогрессии. Последовательность чисел

1.

Повторение:
прогрессии

2. Прогрессии

Арифметическая прогрессия
Геометрическая прогрессия
Последовательность,
в которой каждый член,
начиная со второго,
равен предыдущему,
сложенному с одним и
тем же числом.
Последовательность
отличных от нуля чисел,
в которой каждый член,
начиная со второго,
равен предыдущему,
умноженному на одно и
тоже число.
Число d - разность прогрессии
Число q - знаменатель прогрессии.
d = a2 - a1 = a3 - a2 = a4 - a3 = ….
q = b 2 : b1 = b 3 : b2 = b 4 : b3 = …

3. Формула n-го члена прогрессии

арифметической
an = a1 + d(n - 1)
геометрической
bn = b1·qn - 1
Дано: a1 = 7, d = 5
Дано: b1 = 3, q = 2
Найти: a4.
Найти: b3.
a4 = 22
b3 = 12

4. Характеристическое свойство

Каждый член
последовательности,
начиная со второго, есть
среднее арифметическое
между предыдущим и
последующим членами
прогрессии
an
a n 1 a n 1
2
х1, х2, 4, х4,14, …
найти: х4
Х4 = 9
Каждый член
последовательности,
начиная со второго, есть
среднее геометрическое
между предыдущим и
последующим членами
последовательности (bn >0)
bn
bn 1 bn 1
b1, b2, 1, b4, 16, … - все члены
положительные числа
найти: b4
b4 = 4

5. Формулы суммы n первых членов

арифметическая
геометрическая
a1 an
Sn
n
2
b1 ( 1 q n )
Sn
,q 1
1 q
2a1 d ( n 1 )
Sn
n
2
Дано:
a1 = 5, d = 4
Найти: S5
S5 = 65
b1 qbn
Sn
,q 1
1 q
Дано: b 1 =
2, q = - 3
Найти: S4
S4 = - 40

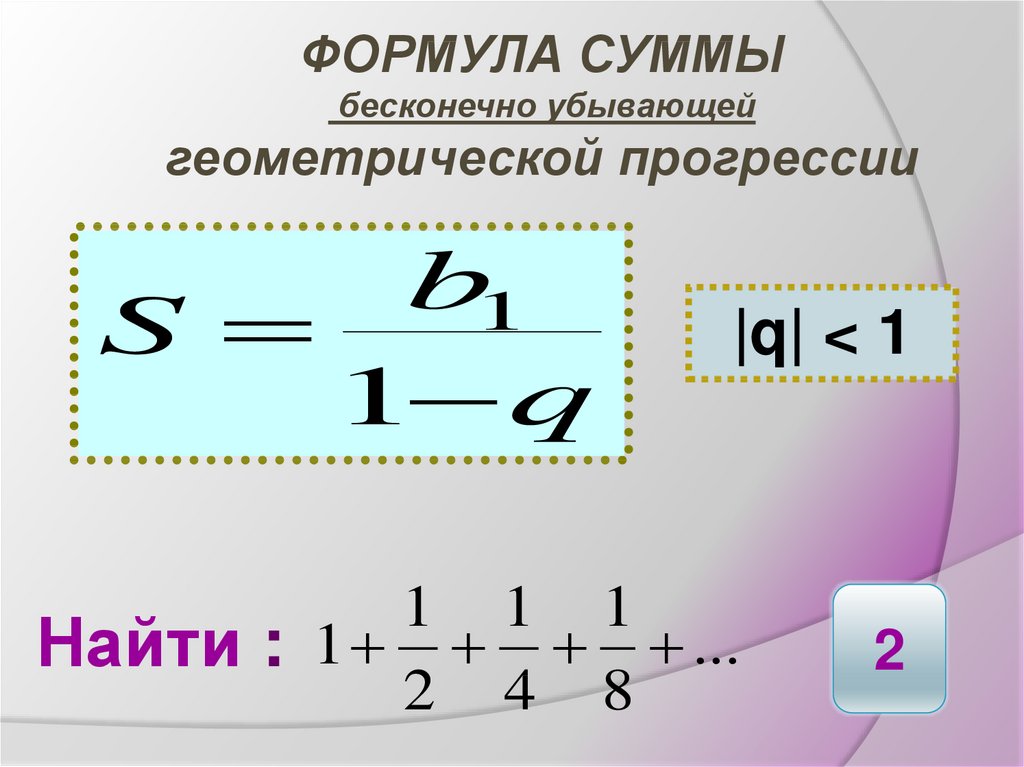
6. ФОРМУЛА СУММЫ бесконечно убывающей геометрической прогрессии

b1
S
1 q
|q| < 1
1 1 1
Найти : 1 ...
2 4 8
2