Машины переменного тока

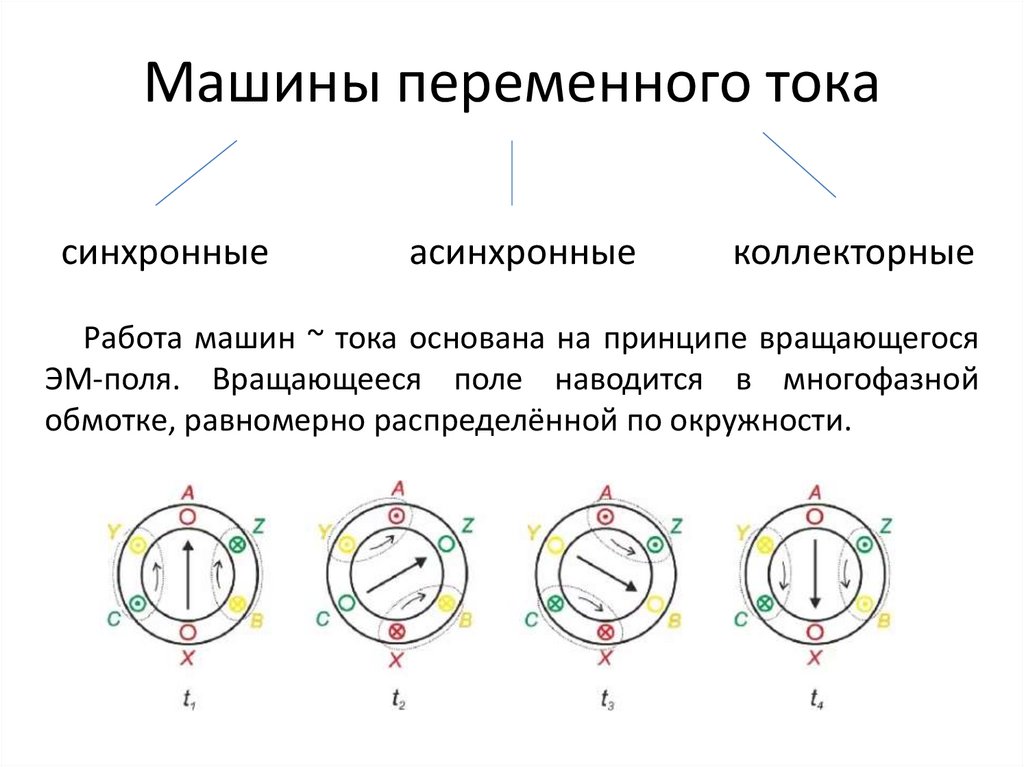
1. Машины переменного тока

синхронные
асинхронные
коллекторные
Работа машин ~ тока основана на принципе вращающегося
ЭМ-поля. Вращающееся поле наводится в многофазной
обмотке, равномерно распределённой по окружности.

2.

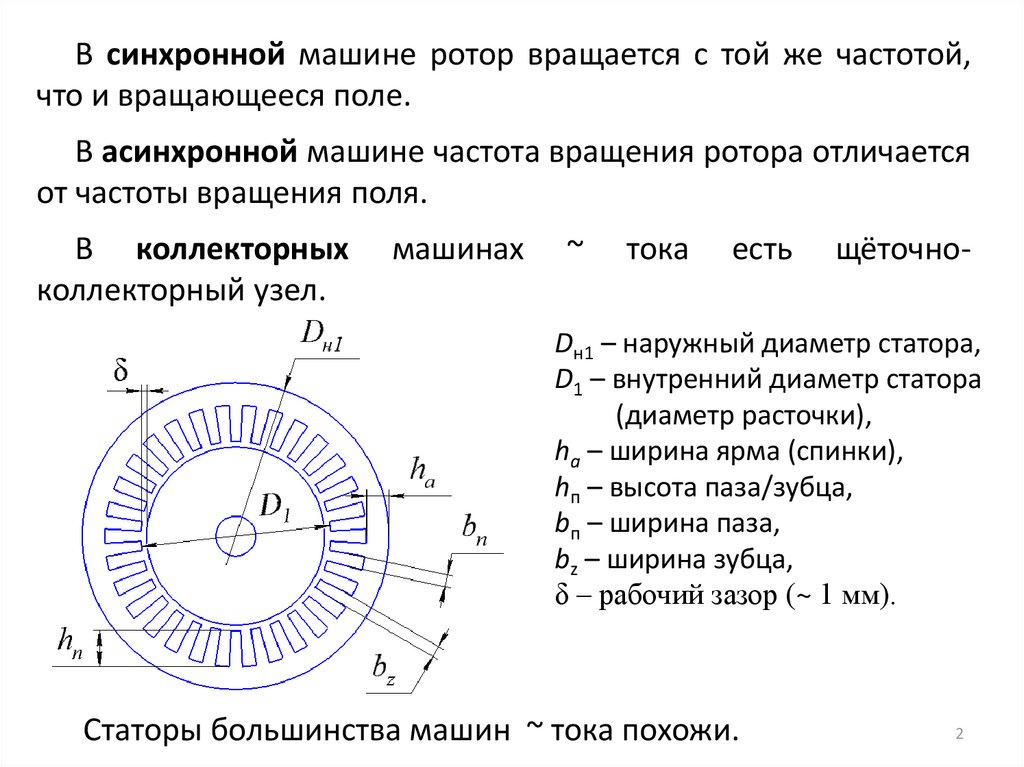
В синхронной машине ротор вращается с той же частотой,
что и вращающееся поле.
В асинхронной машине частота вращения ротора отличается
от частоты вращения поля.
В коллекторных
коллекторный узел.
машинах
~
тока
есть
щёточно-
Dн1 – наружный диаметр статора,
D1 – внутренний диаметр статора
(диаметр расточки),
ha – ширина ярма (спинки),
hп – высота паза/зубца,
bп – ширина паза,
bz – ширина зубца,
δ – рабочий зазор (~ 1 мм).
Статоры большинства машин ~ тока похожи.
2

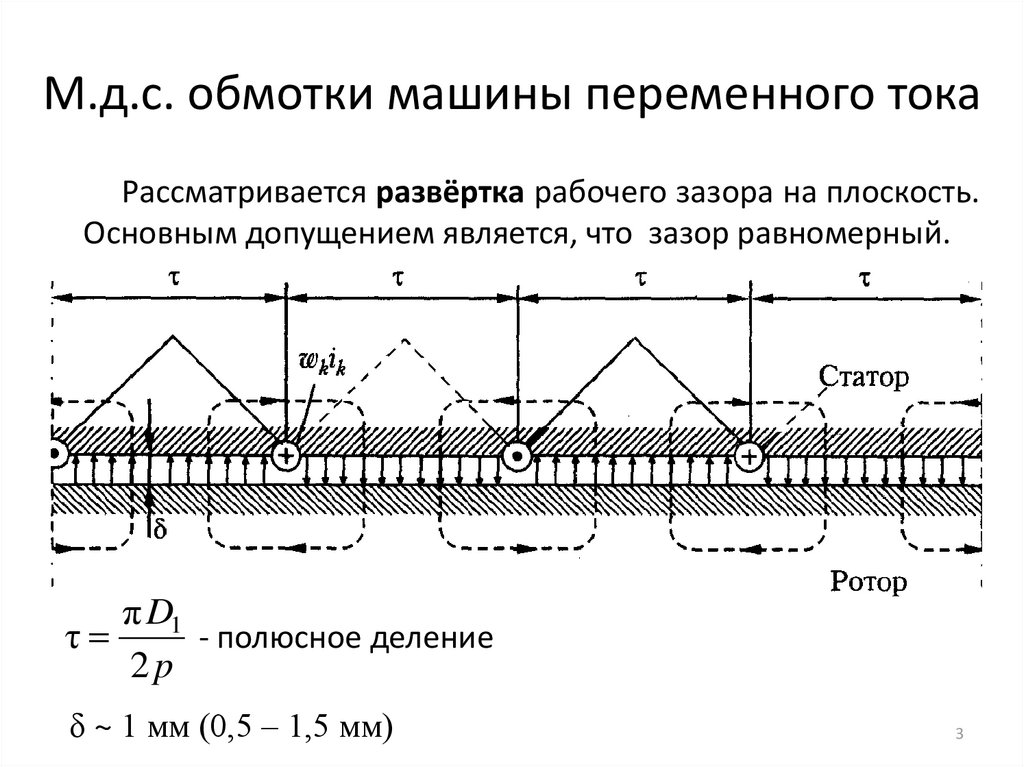
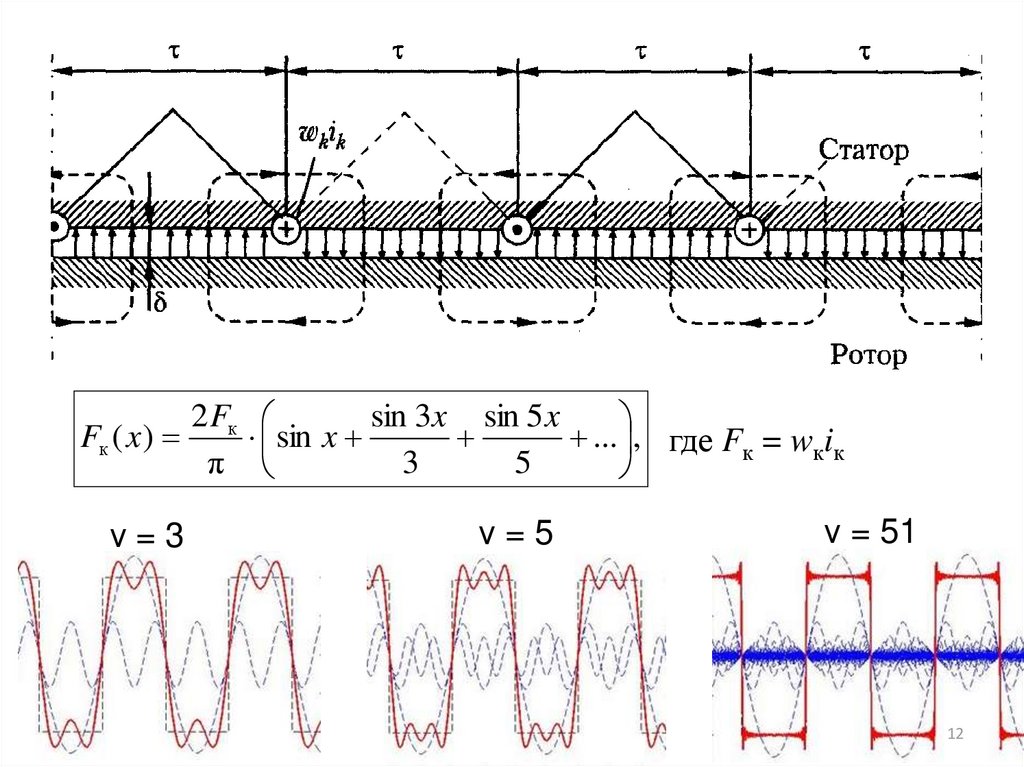
3. М.д.с. обмотки машины переменного тока

Рассматривается развёртка рабочего зазора на плоскость.
Основным допущением является, что зазор равномерный.
π D1
- полюсное деление
τ
2p
δ ~ 1 мм (0,5 – 1,5 мм)
3

4.

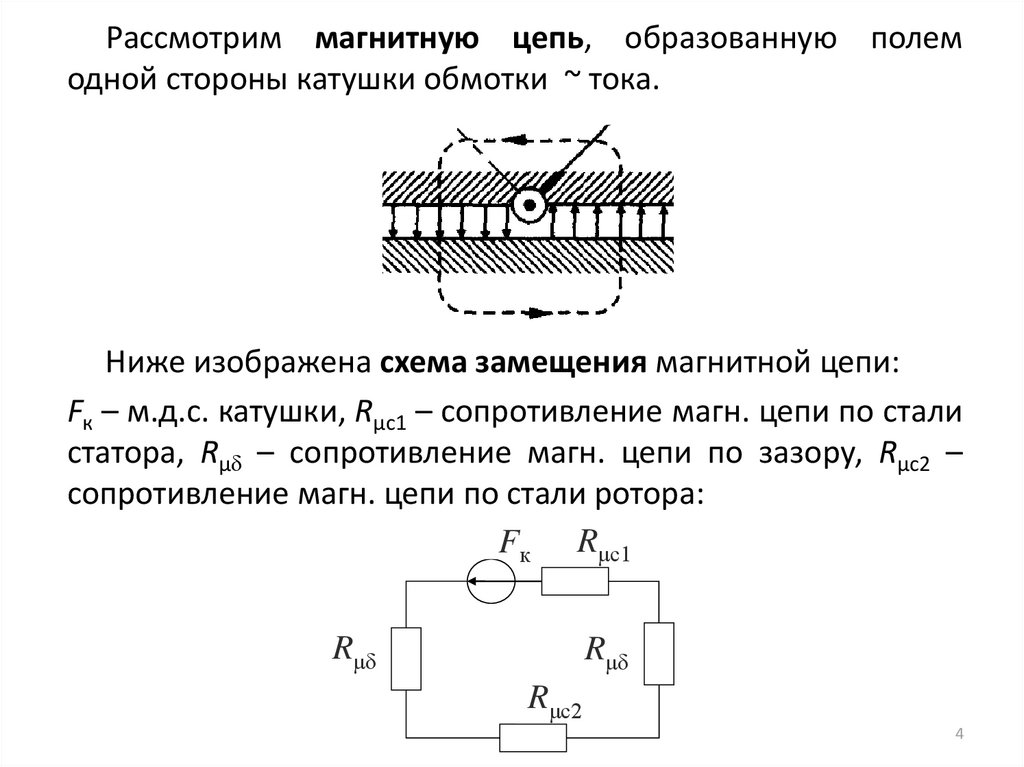
Рассмотрим магнитную цепь, образованную полем
одной стороны катушки обмотки ~ тока.
Ниже изображена схема замещения магнитной цепи:
Fк – м.д.с. катушки, Rμс1 – сопротивление магн. цепи по стали
статора, Rμδ – сопротивление магн. цепи по зазору, Rμс2 –
сопротивление магн. цепи по стали ротора:
Fк Rμс1
Rμδ
Rμδ
Rμс2
4

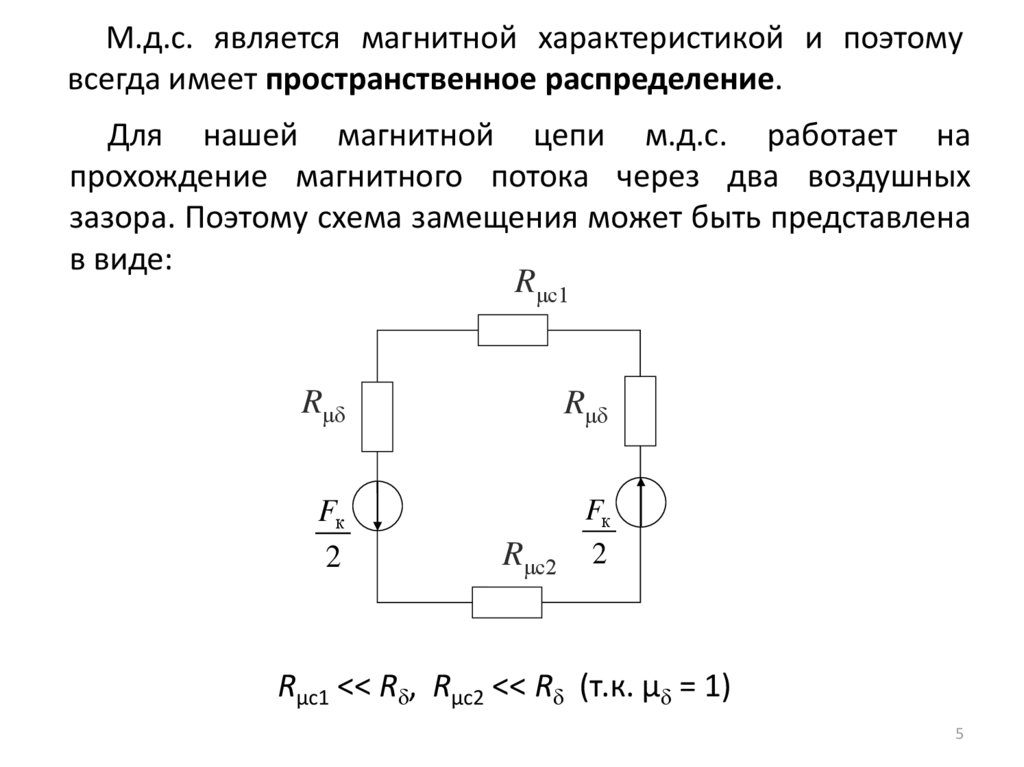
5.

М.д.с. является магнитной характеристикой и поэтому
всегда имеет пространственное распределение.
Для нашей магнитной цепи м.д.с. работает на
прохождение магнитного потока через два воздушных
зазора. Поэтому схема замещения может быть представлена
в виде:
Rμс1
Rμδ
Rμδ
Fк
2
Fк
2
Rμс2
Rμc1 << Rδ, Rμc2 << Rδ (т.к. μδ = 1)
5

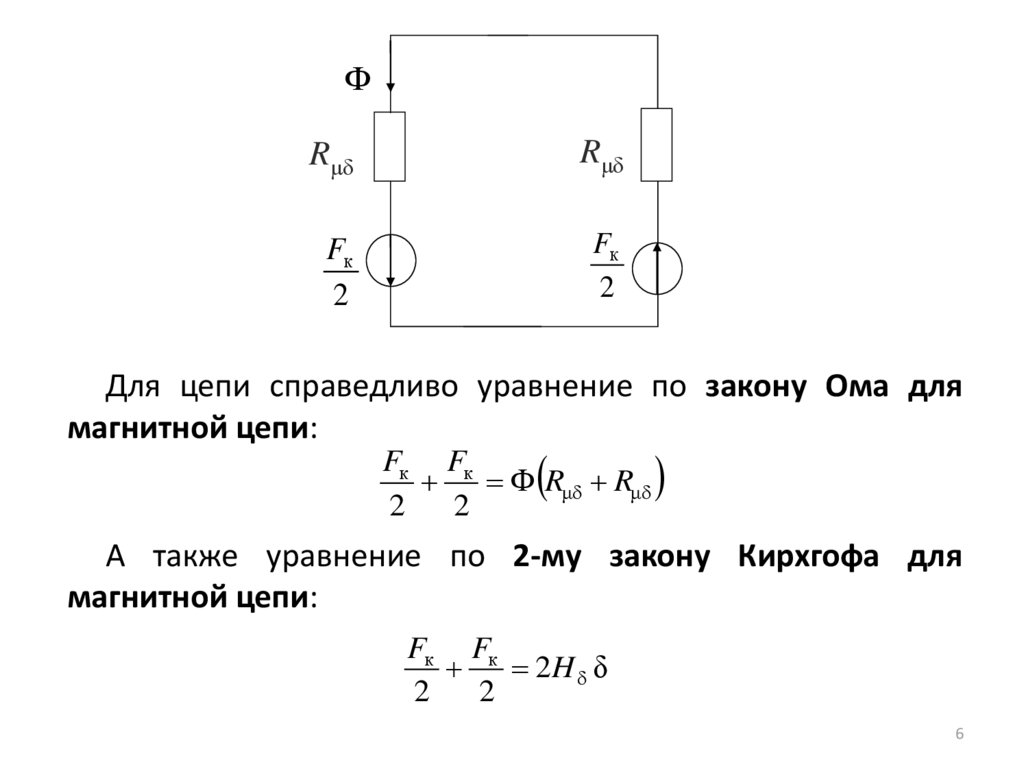
6.

Ф
Rμδ
Rμδ
Fк
2
Fк
2
Для цепи справедливо уравнение по закону Ома для
магнитной цепи:
Fк Fк
Ф Rμδ Rμδ
2
2
А также уравнение по 2-му закону Кирхгофа для
магнитной цепи:
Fк Fк
2H δ δ
2
2
6

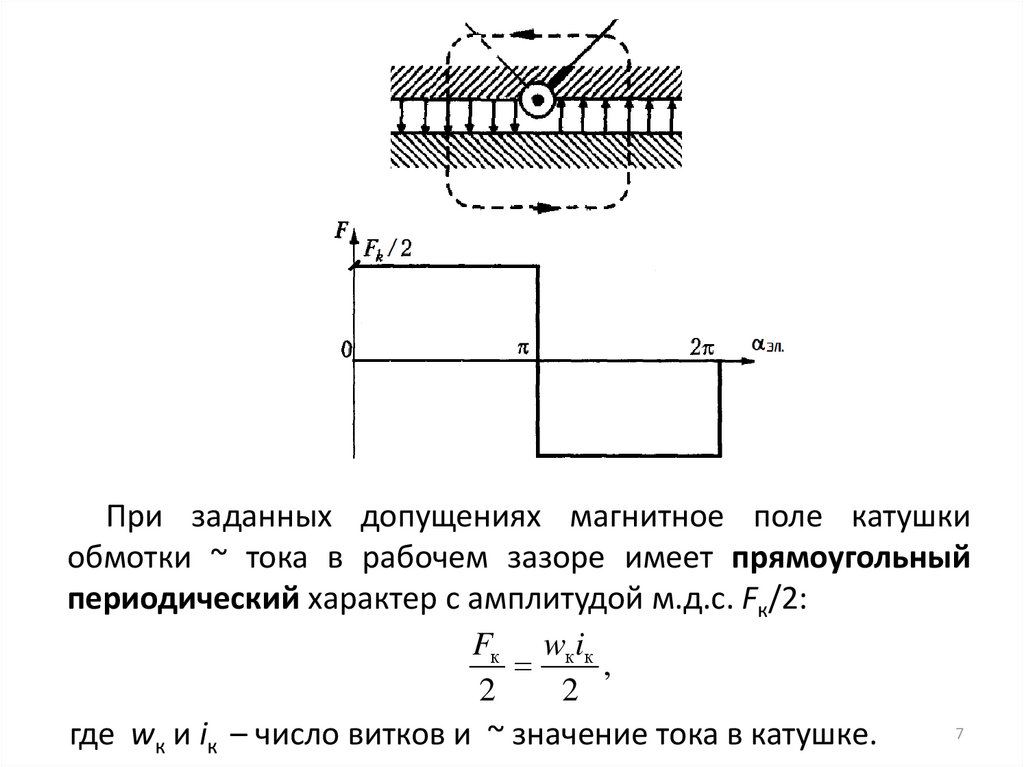
7.

При заданных допущениях магнитное поле катушки
обмотки ~ тока в рабочем зазоре имеет прямоугольный
периодический характер с амплитудой м.д.с. Fк/2:
Fк wкiк
,
2
2
7
где wк и iк – число витков и ~ значение тока в катушке.

8.

Ряд Фурье
Любую периодическую функцию f(x)
можно разложить в тригонометрический ряд
– ряд Фурье:
a0
f ( x ) an cos nx bn sin nx (1)
2 n 1
1768 -1830
- Выражение для коэффициента a0 получается при
интегрировании функции (1) на половине периода:
π
1
a0 f(x)dx
π π
- Выражения для коэффициентов an и bn получаются при
интегрировании на половине периода соответственно
f(x)cosnx и f(x)sinnx:
π
π
1
1
an f(x)cos nx dx, bn f(x)sin nx dx
π π
π π
8

9.

- Если функция f(x) симметрична относительно оси абсцисс,
то коэффициент a0/2 (постоянная составляющая) равен нулю;
- Если функция f(x) нечётная (симметрична относительно
начала координат), то ряд Фурье принимает вид:
f ( x ) bn sin nx
(т.е. an = 0)
n 1
при этом:
π
2
bn f(x)sin nx dx.
π0
9

10.

Наша периодическая прямоугольная функция f(x) нечётная:
π
π
2
2 Fк
Fк
bn f(x)sin nx dx sin nx dx cos nx 0π
π0
π 2 0
πn
Fк
Fк
Fк
n
n
cos nx 1 1 1
1 1 , n 1, 2, ...
πn
πn
πn
Тогда:
Fк 1
f ( x)
1 1 n sin nx
π n 1 n
При чётных n (n = 2, 4, …): f(x) = 0.
10

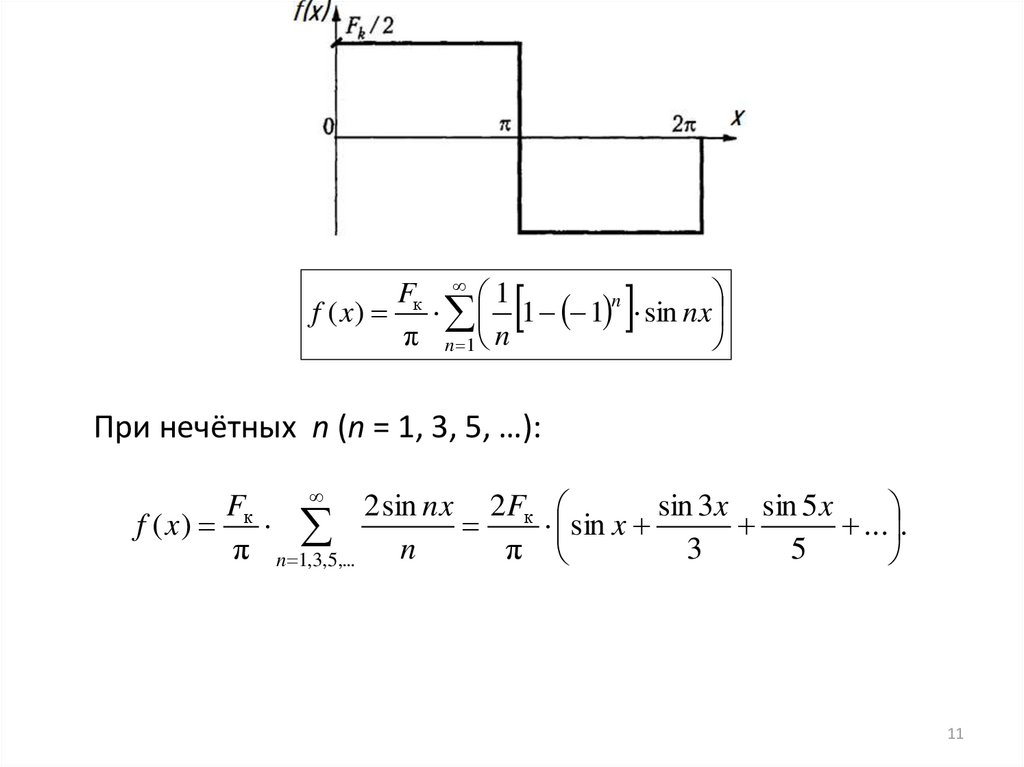
11.

Fк 1
f ( x)
1 1 n sin nx
π n 1 n
При нечётных n (n = 1, 3, 5, …):
Fк
2 sin nx 2 Fк
f ( x)
π n 1,3,5,... n
π
sin 3x sin 5 x
sin x
... .
3
5
11

12.

2 Fк
Fк ( x )
π
ν=3
sin 3x sin 5 x
sin x
... , где Fк = wкiк
3
5
ν=5
ν = 51
12

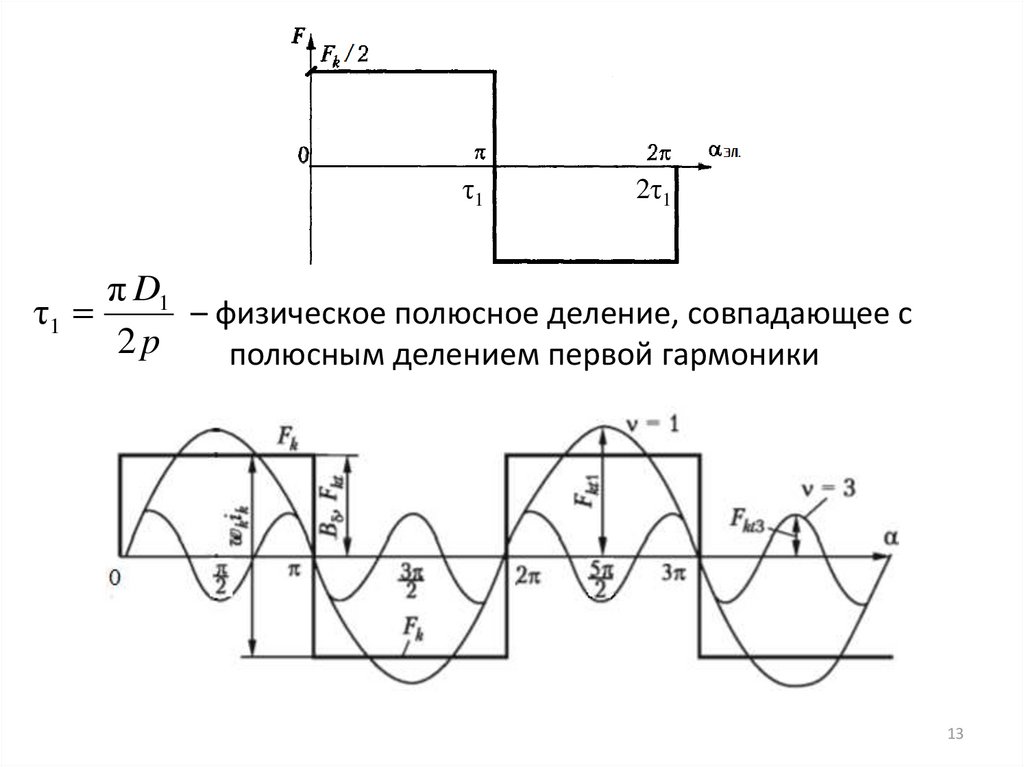
13.

τ1
2τ1
π D1
– физическое полюсное деление, совпадающее с
τ1
2p
полюсным делением первой гармоники
13

14.

М.д.с. катушки переменного тока, выраженная ч/з τ1 :
2 Fк
Fк ( x, τ1 )
π
x
1
3x
1
5x
sin π sin
π sin
π ...
3
τ1
5
τ1
τ1
Т.е. ν - гармоника м.д.с. катушки ~ тока:
2 Fк
νx
Fкν ( x, τ1 )
sin
π
νπ
τ1
(а)
Переменный ток катушки может быть записан в виде:
iк I к max sin ωt
Тогда м.д.с. катушки переменного тока:
Fк wк iк w к I к max sin ωt Fк max sin ωt
(б)
14

15.

2 Fк
νx
Fкν ( x, τ1 )
sin
π
νπ
τ1
Fк Fк max sin ωt
Fкν ( x, τ1 )
νx
sin
π sin ωt,
νπ
τ1
2 Fк max
где Fк max wк I к max
2 wк I к ,
Iк – действующее значение ~ sin-тока в катушке
Амплитуда ν-гармоники м.д.с. катушки ~ sin-тока:
Fкν max
2 Fк max
νπ
2 2 wк I к
wк I к
0,9
.
π
ν
ν
15