Похожие презентации:
Построение сечений многогранника
1. Презентация на тему:
Построение сечениймногогранника.
Выполнила ученица 10 класса
Пименова Ксения.
Учитель математики:
Мазалова Лариса Сергеевна.
2. Содержание
Определение.Примеры
построений сечений.
Задания на построение сечений.
3. Определение
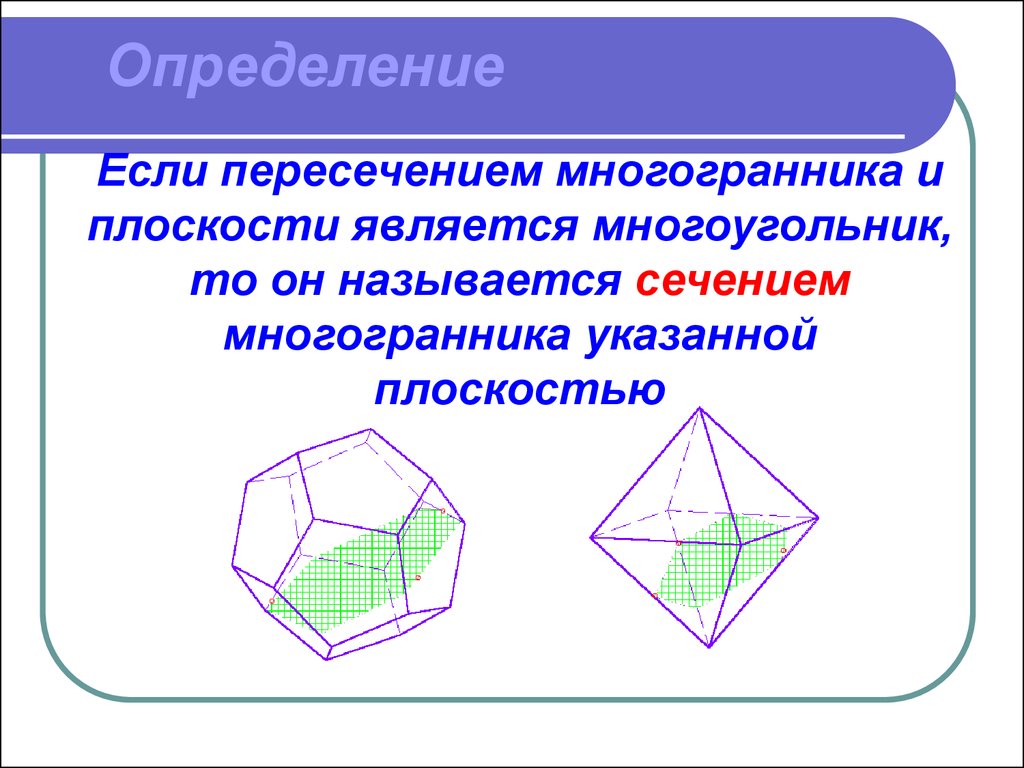
Если пересечением многогранника иплоскости является многоугольник,
то он называется сечением
многогранника указанной
плоскостью
4. Сечение пирамид.
Пирамида – это многогранник,одна из граней которого –
произвольный
многоугольник.
Тетраэдр - это многогранник,
одна из граней которого –
произвольный треугольник.
Так как тетраэдр имеет четыре
грани, то его сечениями
могут быть только
треугольники и
четырехугольники.
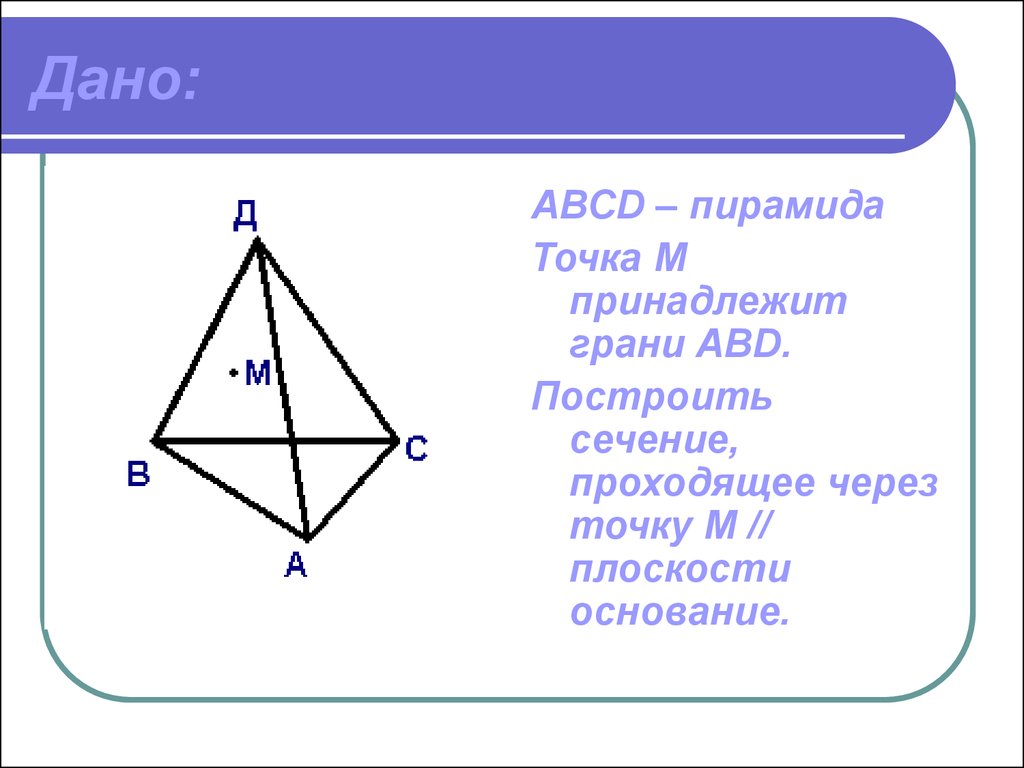
5. Дано:
АВСD – пирамидаТочка М
принадлежит
грани ABD.
Построить
сечение,
проходящее через
точку М //
плоскости
основание.
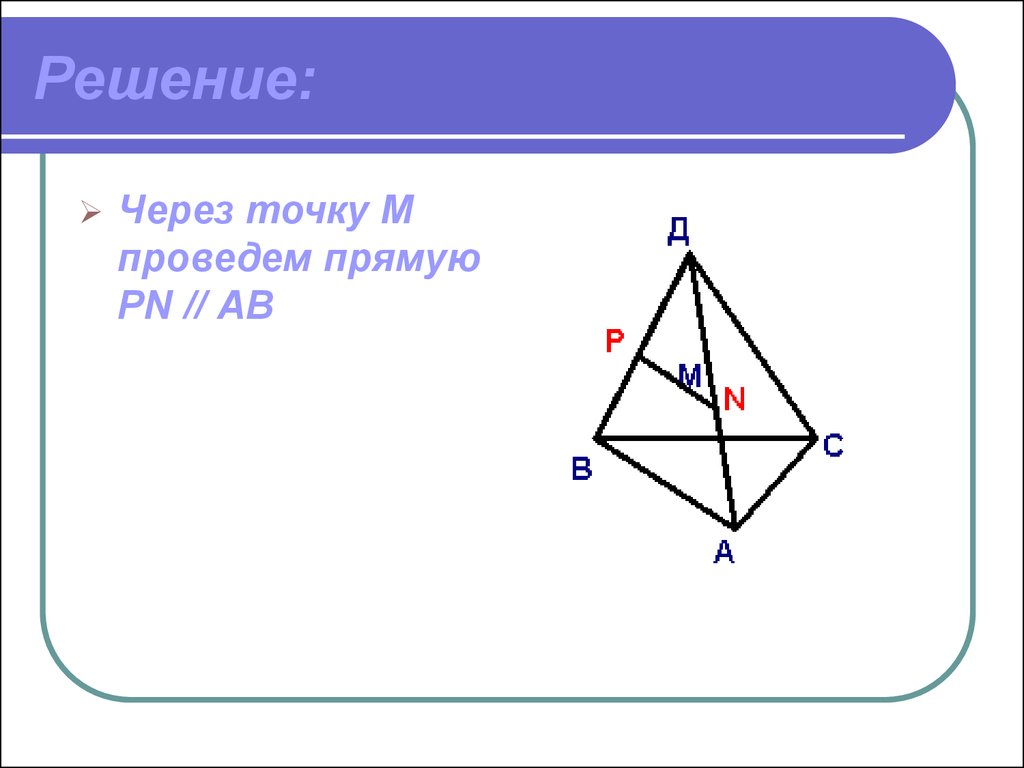
6. Решение:
Через точку Мпроведем прямую
PN // АВ
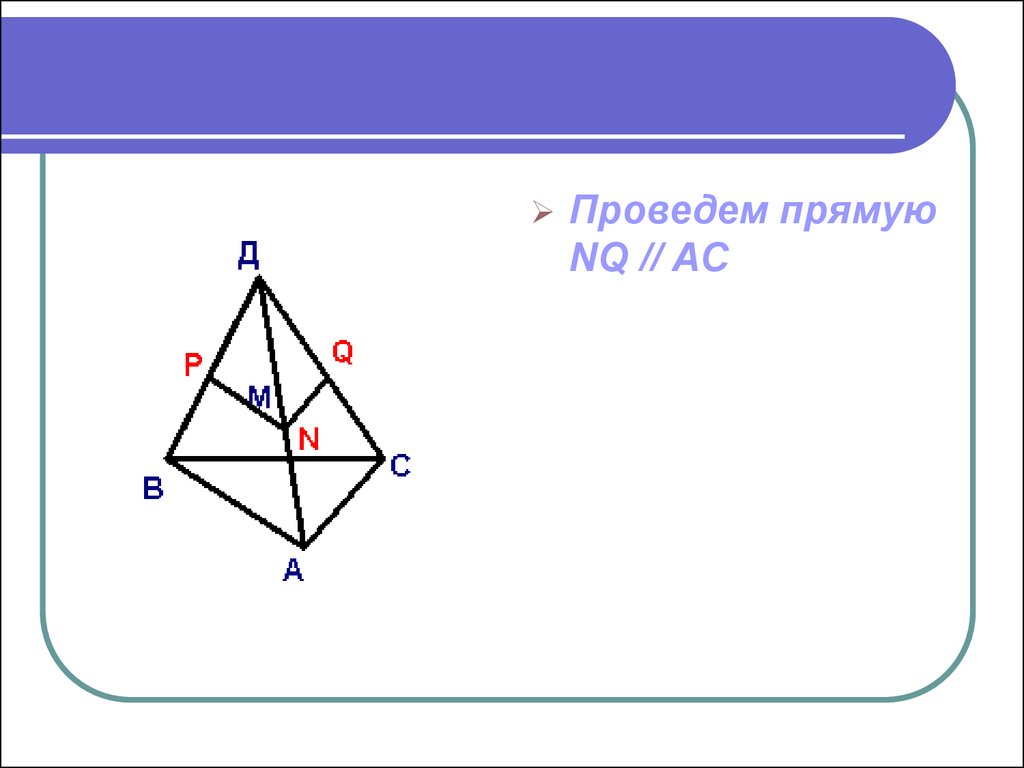
7.
Проведем прямуюNQ // AC
8.
Соединим точки Pи Q.
PNQ- искомое
сечение.
9.
Дано:Пирамида MABCD. Постройте сечение
пирамиды, проходящее через точки P, Q,
R. Известно, что точка P MB, точка R
MA, Q DC.
ВАЖНО!
Если секущая плоскость пересекает
противоположные грани, то она
пересекает их по параллельным
отрезкам.
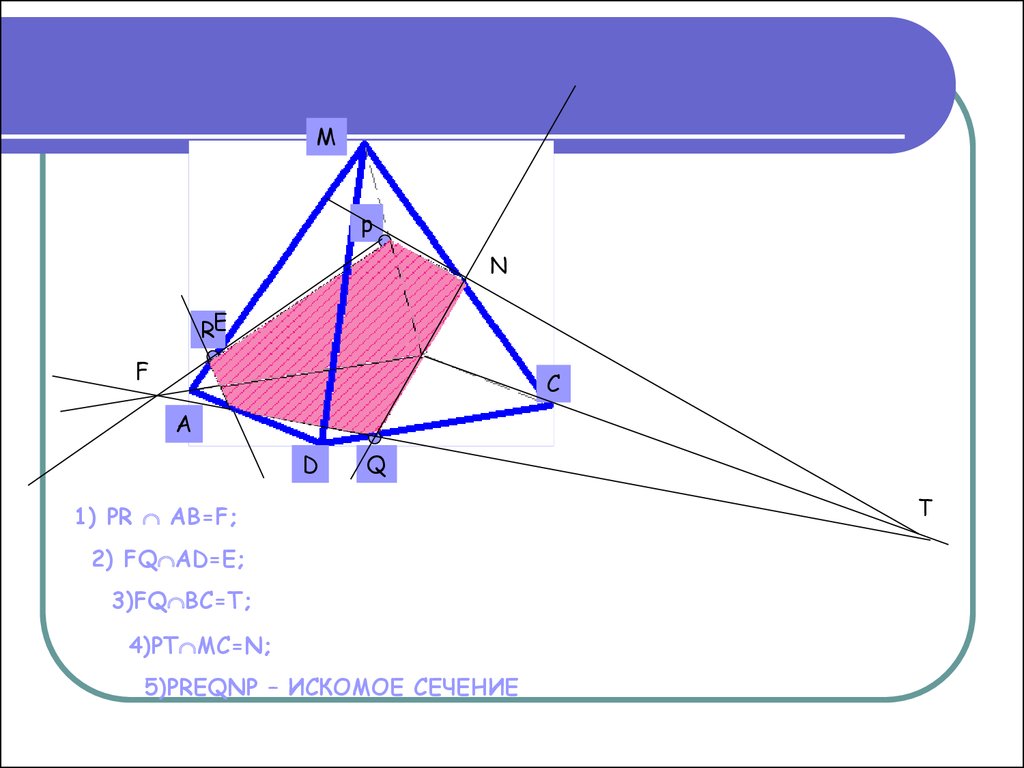
10.
Mp
N
RЕ
B
F
C
A
D
Q
1) PR AB=F;
2) FQ AD=E;
3)FQ BC=T;
4)PT MC=N;
5)PREQNP – ИСКОМОЕ СЕЧЕНИЕ
T
11. Сечение куба
Прямоугольный параллелепипед, укоторого все три измерения равны,
называется кубом.
Куб имеет 6 граней. Его сечениями
могут быть треугольники,
четырехугольники, пятиугольники
и шестиугольники.
12. Дано:
ABCDА1B1C1D1 -куб,точка К
принадлежит
ребру A1В1, точка L
принадлежит
ребру В1C1 , точка
М принадлежит
ребру DC.
Построить:
сечение куба
плоскостью.
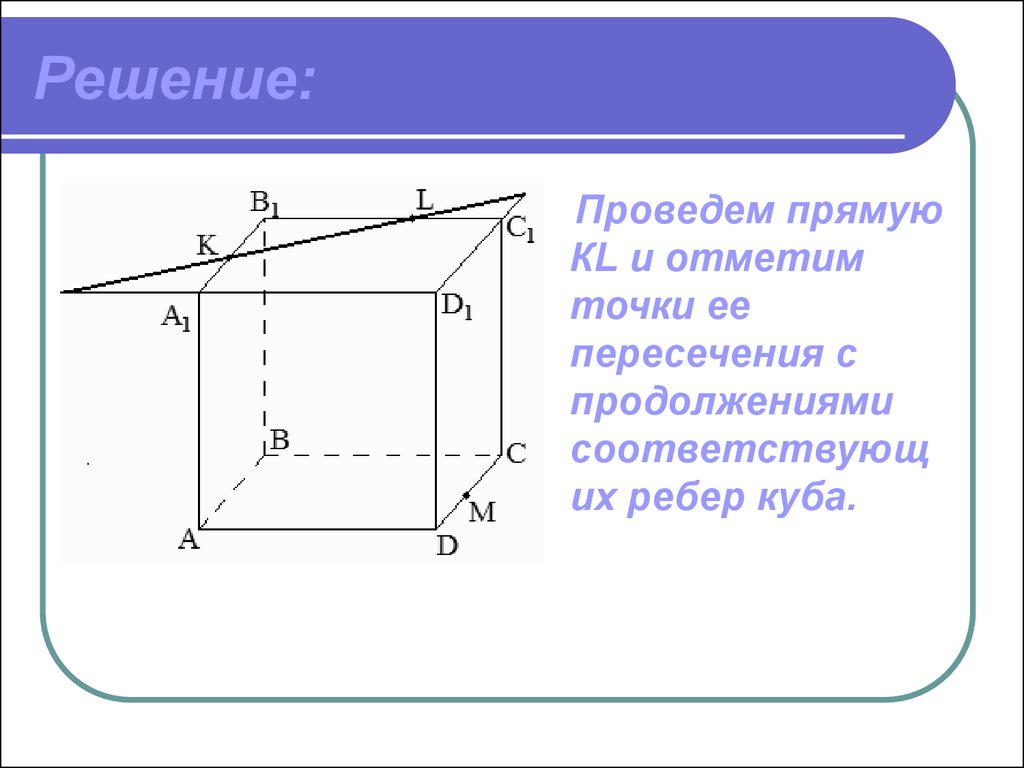
13. Решение:
Проведем прямуюКL и отметим
точки ее
пересечения с
продолжениями
соответствующ
их ребер куба.
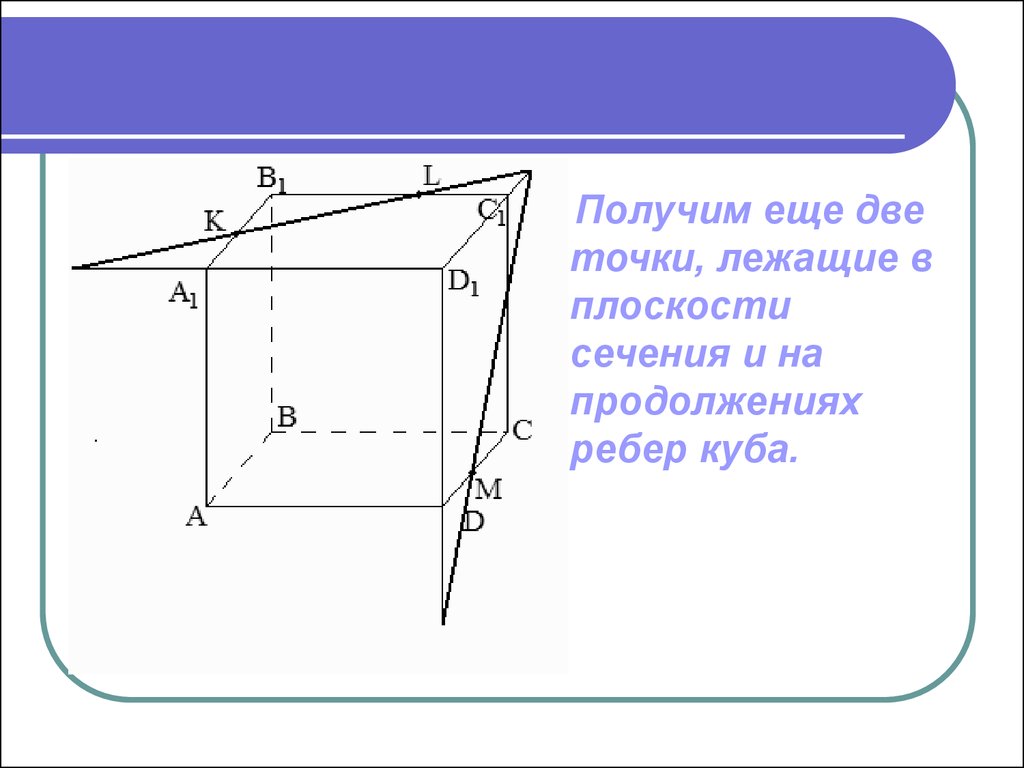
14.
Получим еще дветочки, лежащие в
плоскости
сечения и на
продолжениях
ребер куба.
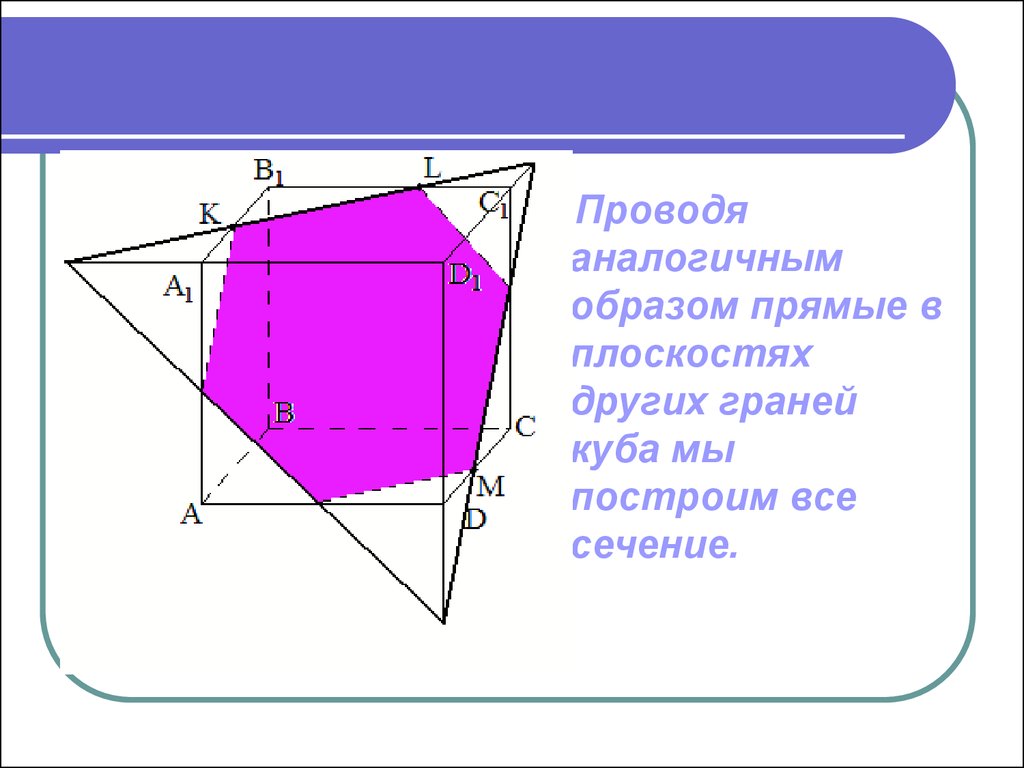
15.
Проводяаналогичным
образом прямые в
плоскостях
других граней
куба мы
построим все
сечение.
16. Дано:
ABCDA1B1C1D1 – куб.Точки PNKQ
принадлежат
ребрам.
Построить сечение
куба плоскостью.
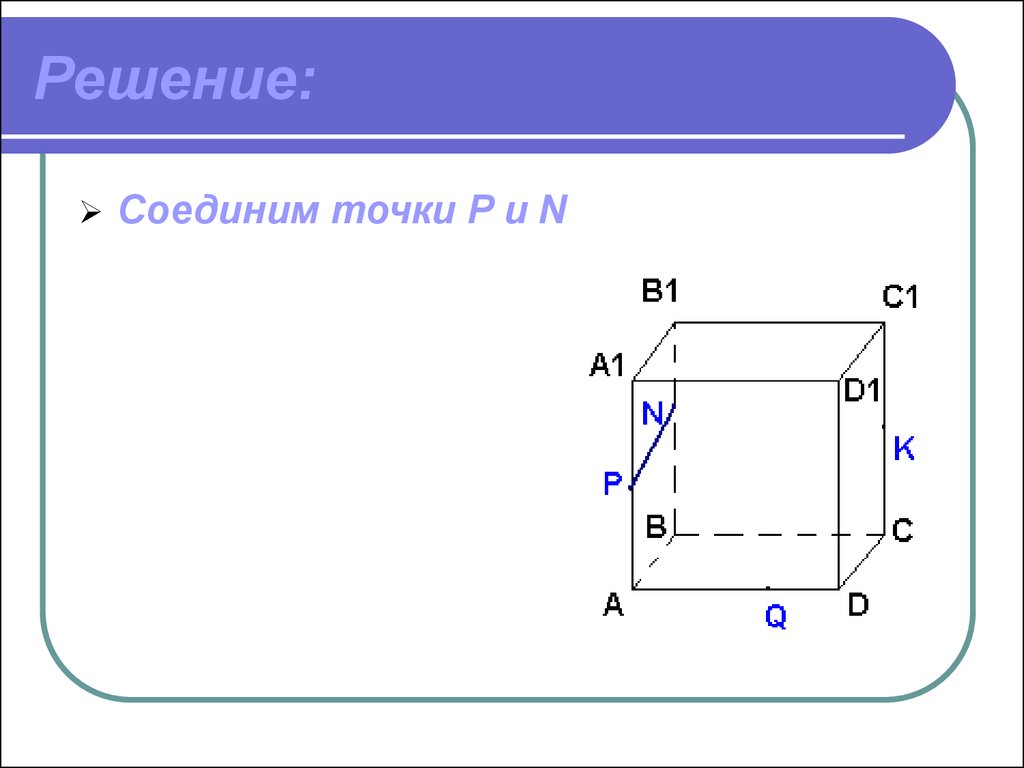
17. Решение:
Соединим точки P и N18.
М – точкапересечения
прямых PQ и DD1
19.
Проведем прямую МК20.
Соединим точки NК.NPQFK – искомое
сечение.
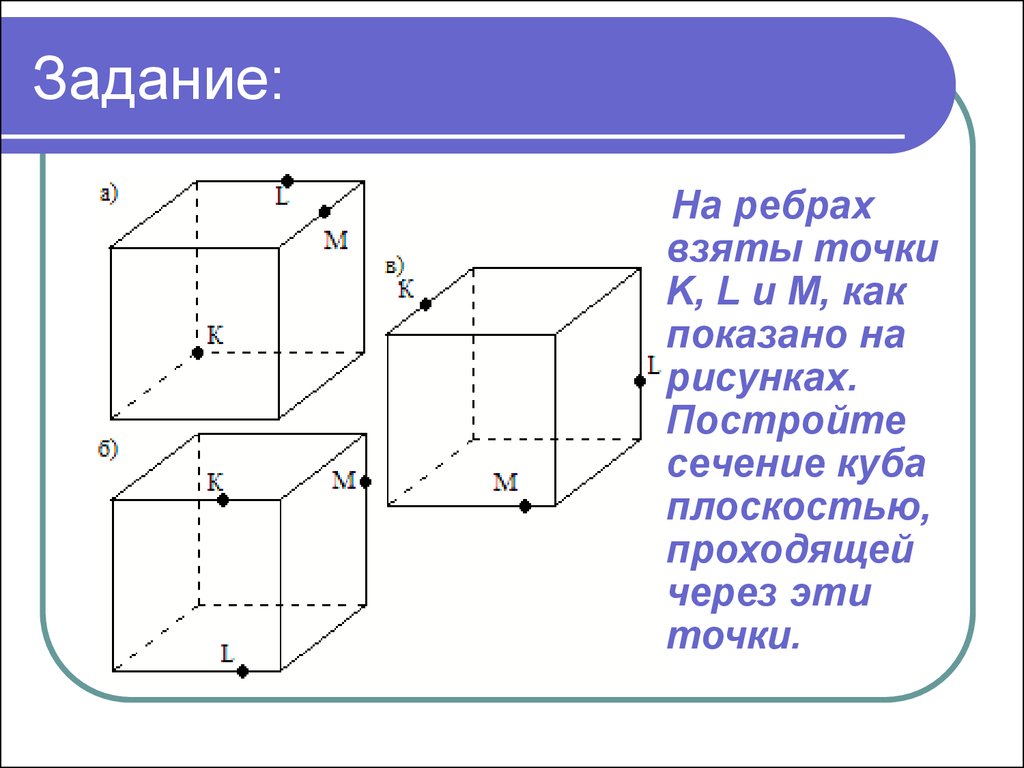
21. Задание:
На ребрахвзяты точки
K, L и M, как
показано на
рисунках.
Постройте
сечение куба
плоскостью,
проходящей
через эти
точки.
22. Ответ к заданию:
23.
24.
«Правильных многогранников вызывающе мало,но этот весьма скромный по численности отряд
сумел пробраться в самые глубины различных
наук»
Л.Кэрролл
25.
Закаждым многогранником
закреплено его значение, НАПРИМЕР:
Тетраэдр является огнём!
26.
куб-земля27.
октаэдр-воздух28. Даже пчёлы знакомы с понятием многогранник!!!
29.
Многогранники в архитектуре.Александрийский
маяк
Великая пирамида в
Гизе



















 Математика
Математика Инженерная графика
Инженерная графика