Похожие презентации:
Метод проекций. Проекции точки
1.
Лекция 1Метод проекций. Проекции точки.
2.
Метод проекцийS
A
А
П – плоскость
проекций;
А – произвольная
точка пространства;
S
проекций;
SA– –центр
проецирующий
луч;
А – проекция точки А
на плоскость
А = SA
проекций
ПП
При проецировании проецирующие лучи проходят через центр проекций
– точку S . Проекция А точки А есть пересечение проецирующего луча
SA с плоскостью проекций П .
3.
Классификация проекцийЦентральные
(конические)
S
Параллельные (цилиндрические)
косоугольные, s П
ортогональные, s П
B
A
B
A
B
s
C
C
А
С
С
C
А
В
В А
A
В
С
При центральном проецировании совокупность проецирующих лучей
образует коническую поверхность. При параллельном проецировании
совокупность проецирующих лучей образует цилиндрическую
поверхность.
s
4.
Ортогональное проецированиеs
A
А1
При ортогональном
проецировании
проецирующие лучи s
перпендикулярны
плоскости проекций П1
и параллельны между
собой
Прямая задача – изобразить на чертеже положение точки. Произвольной
точке пространства А на плоскости проекций соответствует ее
единственное изображение – проекция А1 . Проецирование на одну
плоскость проекций дает решение прямой задачи
5.
Метод МонжаМетод ортогонального проецирования:
• плоскости проекций перпендикулярны
между собой;
• проецирующие лучи перпендикулярны
плоскости проекций.
Для однозначного определения положения точки
в пространстве необходимо задать на чертеже
минимум две ее ортогональные проекции
Комплексный чертеж – это изображение
геометрического образа, полученное при
совмещенных плоскостях проекций
6.
Точка в системе трех плоскостей проекцийПространственная картина
z
П2
x
O
П1 П2 П3
y
Используются три основные взаимно перпендикулярные плоскости
проекций: П1 - горизонтальная; П2 - фронтальная; П3 - профильная.
Плоскостей проекций пересекаются по осям Оx, Оy, Оz декартовой
системы координат
7.
Точка в системе трех плоскостей проекцийПространственная картина
z
Комплексный чертеж
П2
П2
O
x
z
П3
y3 x
П1
П1
y1
y
O
П3
y3
y1
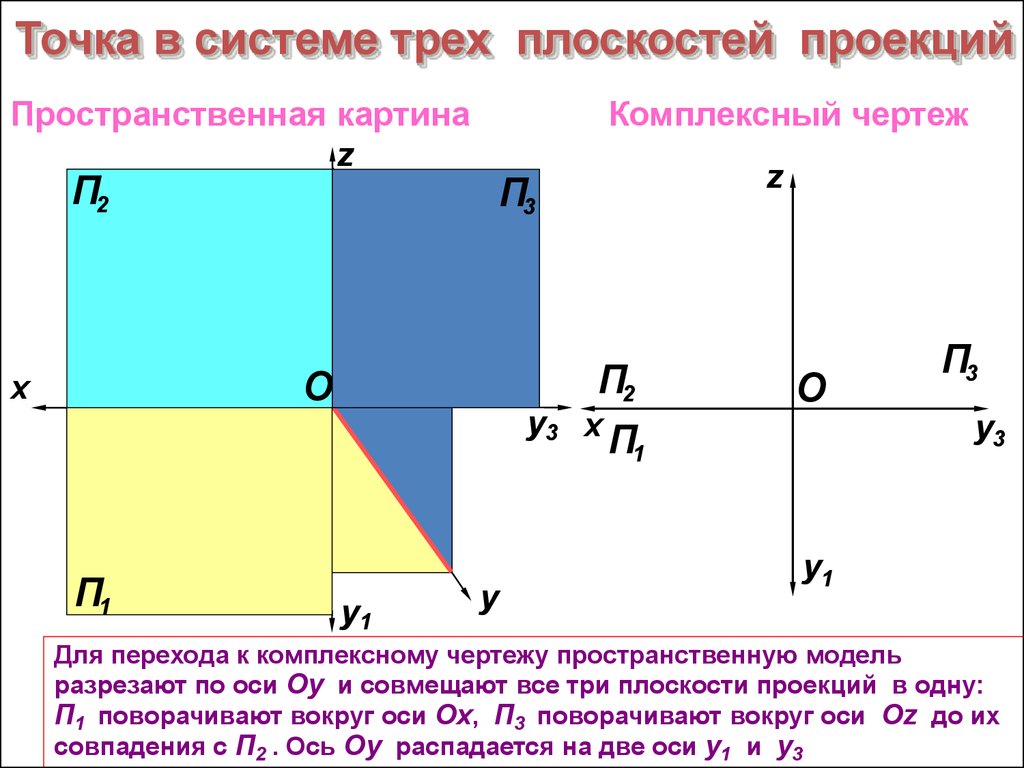
Для перехода к комплексному чертежу пространственную модель
разрезают по оси Оy и совмещают все три плоскости проекций в одну:
П1 поворачивают вокруг оси Оx, П3 поворачивают вокруг оси Оz до их
совпадения с П2 . Ось Оу распадается на две оси y1 и y3
8.
Точка в системе трех плоскостей проекцийПространственная картина
z
П2
А2
Комплексный чертеж
z
Аz
A
x
Аx
O
А1
А3
Аy
П2
O
xП
П3
y3
1
y1
АА1 П1АА
; 2 П2 АА3 П3y
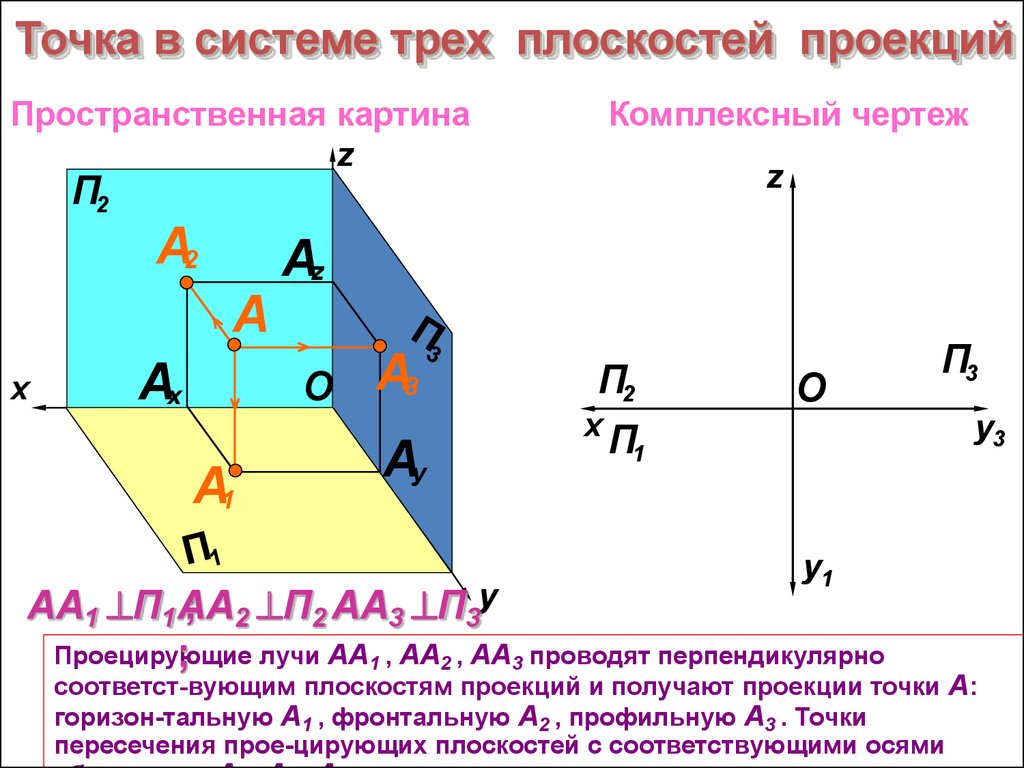
Проецирующие
лучи АА1 , АА2 , АА3 проводят перпендикулярно
;
соответст-вующим плоскостям проекций и получают проекции точки А:
горизон-тальную А1 , фронтальную А2 , профильную А3 . Точки
пересечения прое-цирующих плоскостей с соответствующими осями
9.
Точка в системе трех плоскостей проекцийПространственная картина
z
Комплексный чертеж
П2
А2
Аz
Аx
А1
П1
А2
А3
A
x
z
П3
А3
O
y3
Аy
А1
y1
y
x
Аz
Аx
O
А3
Аy
3
y3
А1 Аy
1
y1
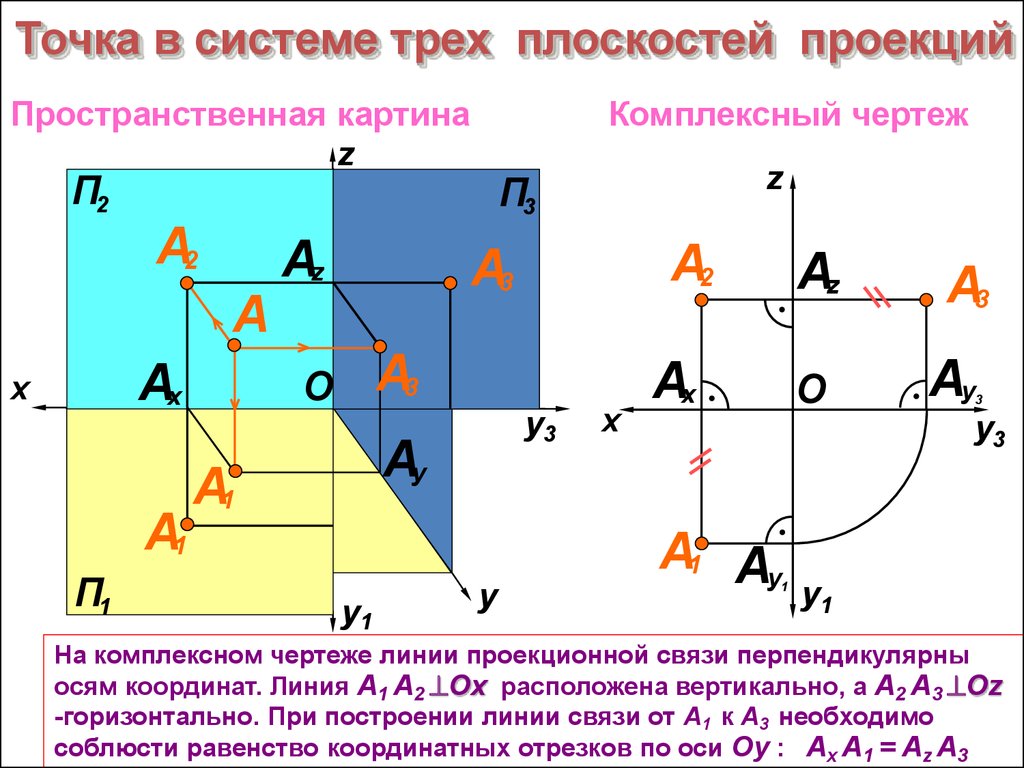
На комплексном чертеже линии проекционной связи перпендикулярны
осям координат. Линия А1 А2 Ох расположена вертикально, а А2 А3 Оz
-горизонтально. При построении линии связи от А1 к А3 необходимо
соблюсти равенство координатных отрезков по оси Оy : Ax A1 = Az A3
10. Безосный чертеж
П2П2
А2
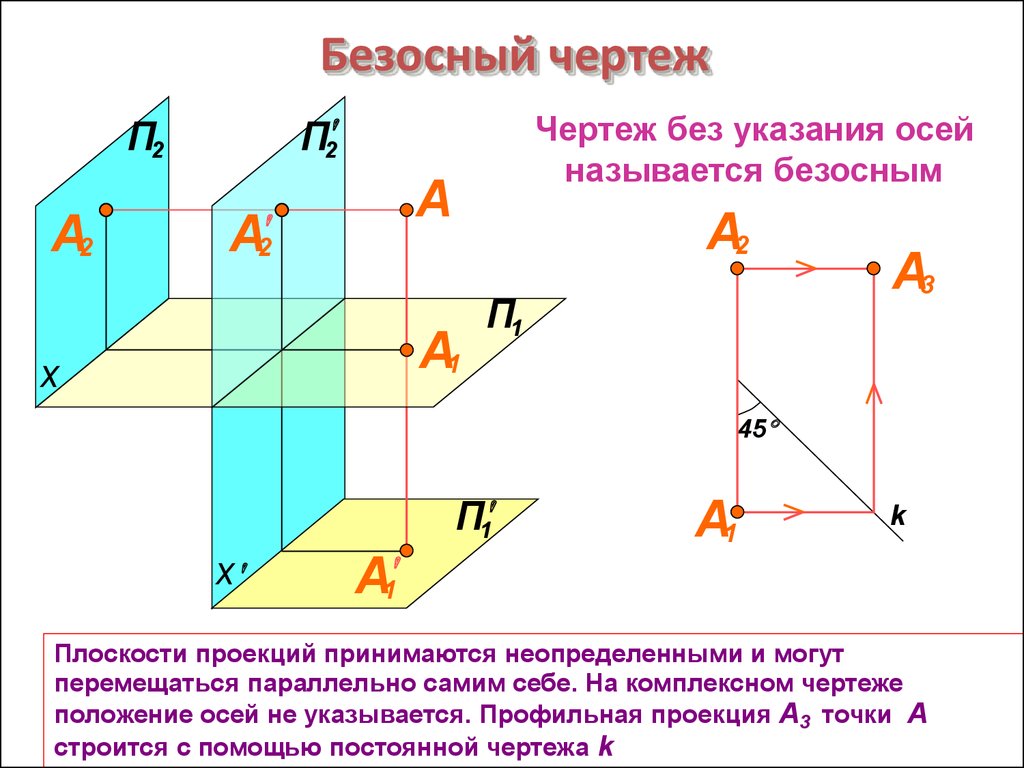
Чертеж без указания осей
называется безосным
А
А2
А2
А1
x
П1
А3
45
П1
x
А1
А1
k
Плоскости проекций принимаются неопределенными и могут
перемещаться параллельно самим себе. На комплексном чертеже
положение осей не указывается. Профильная проекция А3 точки А
строится с помощью постоянной чертежа k
11.
Прямоугольные координаты точкиz
П2
А2
y
x
A(xA ,yA ,zA )
Аz
A xA
Аx A
А1
O
zA
xA = AA3
yA = AA2
zA = AA1
А3
Аy
y
Система трех взаимно перпендикулярных плоскостей проекций - аналог
декартовой системы координатных плоскостей. Координата точки есть
число, выражающее ее расстояние до плоскости проекций. Точка А в
пространстве имеет координаты: абсциссу XA , ординату YA , аппликату ZA
12.
Прямоугольные координаты точкиz
А2
y
А2
zA
A
zA
O
O
x
x
xA
y
A
А1
xA
y
A
А1
А3
zA
y3
y1
На комплексном чертеже численные значения координат откладываются
вдоль соответствующих координатных осей. Каждая проекция точки
определяется двумя координатами: горизонтальная – XA и YA ,
фронтальная - XA и ZA , профильная - YA и ZA .
13.
Конкурирующие точкиКонкурирующими называются точки, лежащие на
одном проецирующем луче.
П2
В2
A2
B2
А2
В
z
A
В1 (A1)
zB > zA
z
x
В1 (A1)
Горизонтально конкурирующие точки А и В лежат на общем
горизонтально-проецирующем луче, поэтому их горизонтальные
проекции совпадают. Точка В выше точки А и расположена ближе к
наблюдателю, ее горизонтальная проекция В1 будет видимой
14.
Конкурирующие точкиВидима та точка, у которой больше координата
П2
В2 (A2)
A y
В
A1
В1
В2 (A2)
x
А1
B1
y
yB > yA
Фронтально конкурирующие точки А и В отличаются только
координатой y , лежат на одном фронтально-проецирующем луче,
поэтому их фронтальные проекции совпадают. Ближе к наблюдателю
расположена точка В, ее фронтальная проекция В2 будет видимой
15. Преобразование чертежа Монжа
16. Способ перемены плоскостей проекций
П2 П4П4 П1
П4 П1=x1
П2
А2
А
zА
x
А1
А4
П4
z П4= z П2
П1
zА
x1
Чертеж:
А2
П2
x
П1
А1
zА
x1
П1 П
4
zА
А4
Заменим исходную фронтальную плоскость проекций П2 на новую
плоскость проекций П4. При этом преобразовании расстояние точек от
плоскости П1 (координата z) остается неизменным
17. Способ вращения вокруг проецирующей прямой
Сущность способа:геометрический образ
вращают вокруг проецирую-щей
оси до частного положения
А – произвольная
точка;
i – ось вращения;i П2
П2
А2
i2
i
x
Чертеж:
A
А1
А2
П2
x
П1
i1
А1
А2
i2
А1
i1
При вращении точка описывает окружность, расположенную в плоскости
уровня. Если ось вращения i П2 , то на П2 траектория движения точки
проецируется в натуральную величину (окружность с центром в точке i2 )
На П1 она проецируется в виде прямой, проекции оси вращения i1
18. Способ вращения вокруг проецирующей прямой
П2i2
А2
x
i
A
А1 i 1
А–
произвольная
точка;
i – ось вращения;
i П1
Чертеж:
А2
П2
x
П1
А1
i2
А2
А1
i1
При горизонтально проецирующем положении оси вращения траектория
движения точки на П1 проецируется в натуральную величину, т.е. в виде
окружности с центром в точке i1 . На П2 она будет проецироваться в
виде прямой линии, перпендикулярной проекции оси вращения i2
19. Способ плоскопараллельного перемещения
Сущность способа: геометрический образ переводится в частное положениеплоскопараллельным движением его точек по плоскостям уровня
П
А 2
Г2 А2
2
x
А – произвольная точка;
Г – плоскость
перемещения;
A
А1
А
Г
А1
Г
П1 ;
Г
П2
Схема:
А2
П2
x
П1
А1
А2 Г
2
А1
При плоскопараллельном перемещении траектория движения горизон-тальной
проекции точки повторяет ее перемещение в плоскости Г. На П2 фронтальная
проекция точки перемещается по следу плоскости Г2 , который параллелен
оси х
20. Способ плоскопараллельного перемещения
П2
x
А2
А2
A
А1
А – произвольная точка;
Ф – плоскость
перемещения;
А Ф
Ф
П2;
Ф
П1
Схема:
А1 Ф1
А2
П2
x
П1
А1
А2
А1 Ф
1
На П2 траектория движения фронтальной проекции точки повторяет ее
перемещение в плоскости Ф, поэтому расположение проекции может быть
произвольным. На П1 горизонтальная проекция точки перемещается по следу
плоскости Ф1 , который параллелен оси х
















 Математика
Математика Инженерная графика
Инженерная графика








