Похожие презентации:
Экологическое моделирование. Модель одновидовых популяции при отсутствии ограничений
1. Экологическое моделирование
Модель одновидовых популяциипри отсутствии ограничений.
2. Модель одновидовых популяции при отсутствии ограничений
В большом пруду разводят рыб. Онине мешают друг другу: пищи, света,
места хватает, хищники отсутствуют,
рыбу вылавливают.
Как будет меняться популяция с
течением времени?
3. Постановка задачі.
Введем обозначения:N0 - количество особей в начале
наблюдения (момент времени t = 0)
N - численность популяции в
произвольный момент времени t
Δ N - прирост численности за Δ t
(достаточно малый)
Δ N / Δ t - средняя скорость прироста
за Δ t
4.
Факторы, влияющие на прирост:А - коэффициент рождаемости
В - коэффициент смертности
Δ N = N * A-N * B = N * (A-B)
A> B A <B
5.
K=A-BКоэффициент прироста количественная
характеристика внутренней
способности популяции к выживанию
6.
В природных условиях:1) коэффициент прироста меняется с
течением времени
2) воспроизведение особей
осуществляется постоянно
7. предположение 1.
При неизменных внешних условиях k постоянная во времени величина.Поэтому:
Ni + 1> Ni
Δ N / Δ t - растет и зависит от Ni
8. Припущення 2.
Зависимость средней скоростиприроста от численности популяции прямо пропорциональна:
Δ NE / Δ t = k * N (1)
или
Δ N = k * N * Δ t (2)
Прирост численности
пропорционален:
1) Ni 2) Δ t
9. Зауваження:
Все утверждения верныдля достаточно малых значений
Δ t nf Δ N
Δ t - условная единица
10. Таким образом из (1) и (2):
k = Δ N / (N * Δ t)K - относительный прирост Δ N / N за
единицу времени
11. ∆ N/ ∆ t = k*N (1)
1798 р.Рівняння Томаса
Мальтуса
“модель Мальтуса”
12. Метод пошагового решения уравнения Мальтуса
13. решение:
При t = 0 N = N 0, ΔN = 0В конце Δt согласно (2) ΔN = k * Nj-1 *
Δt Nj = Nj-1 + ΔN (3)
или Nj = Nj-1 + k * Nj-1 * Δt (4)
(4) (2), (3)
Повторяем 2), 3) для ti = ti-1 + Δt
14. Математична модель одновидової популяції за відсутності обмежень.
∆ N = k*N *∆ t(2)
Ni = Nj-1+∆N (3)
або
Ni = Nj-1+ k*Nj-1*∆t
(4)
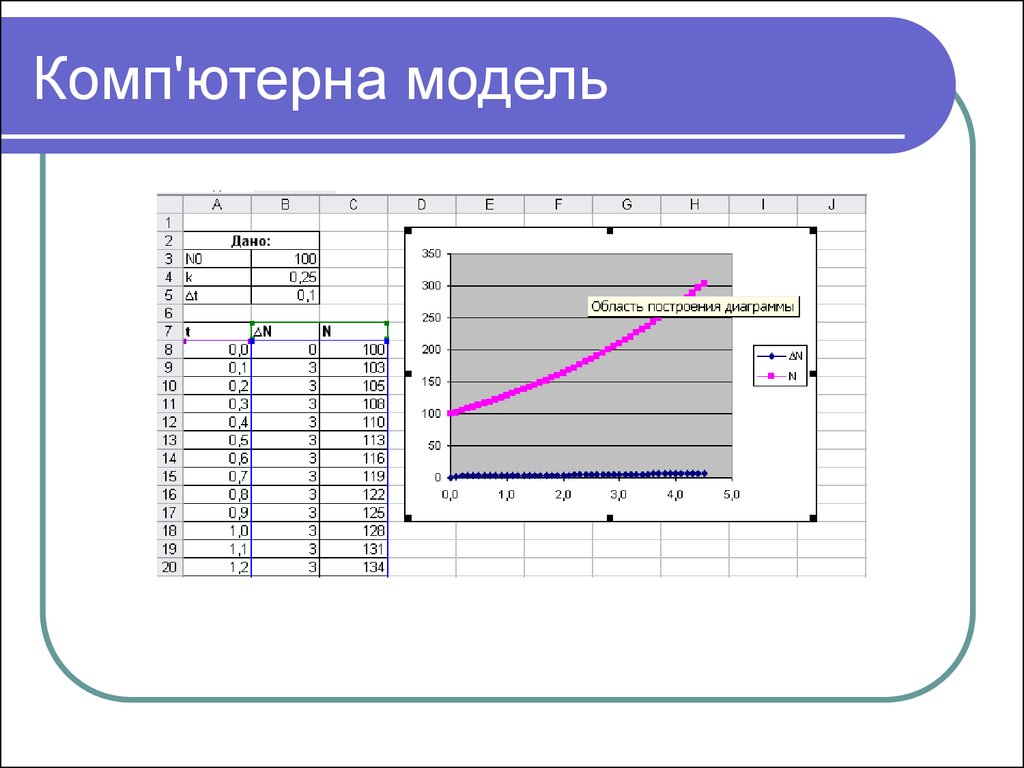
15. Комп'ютерна модель
16. Питання для аналізу моделі:
Як за таблицею встановити, що зростаннячисельності не є лінійним?
Через який час початкова чисельність
подвоїться? Ще раз подвоїться?
Чи через однаковий час подвоюється
чисельність?
Чи виконується така закономірність для ∆N
?
Знайдіть на декількох довільних однакових
проміжках часу Nпочаткова /Nкінцева. Зробить
висновки.
17. Зауваження:
Аналітичне розв'язання рівняння (1):N=N0ekt
E=2.718…
число Ейлера
18. Висновки:
при k>0зростання чисельності популяції
з плином часу
необмежене.
19. Висновки:
Будь-яка модель є адекватною умежах прийнятих припущень.
Результати моделювання можуть бути
хибними за таких причин:
необґрунтованість припущень
екстраполяція моделі
нехтування суттєвими факторами


















 Экология
Экология








