Похожие презентации:
Интерполяционные формулы Гаусса, Стирлинга, Бесселя
1. Интерполяционные формулы Гаусса, Стирлинга, Бесселя
2.
Пусть точка х лежит в окрестности серединыинтервала содержащего 2n+1 равноотстоящих с
шагом h узла интерполирования
x n x ( n 1) ... x 1 x0 x1 ... xn 1 xn
3.
• Для интерполирования функции f(x) в этойточке можно использовать первой (х0<x) или
второй (x0>x) интерполяционными формулами
Гаусса.
x x0
• Обозначим q
h
4.
• Первая интерполяционная формула Гауссаимеет вид:
q(q 1) 2
(q 1)q(q 1) 3
Pn ( x) y0 q y0
y 1
y 1
2!
3!
(q n 1)...(q n 1) 2 n 1
y ( n 1)
(2n 1)!
(q n 1)...(q n) 2 n
y n
(2n)!
5.
• Вторая интерполяционная формула Гаусса имеетвид:
q (q 1) 2
(q 1)q (q 1) 3
Pn ( x) y0 q y 1
y 1
y 2
2!
3!
(q n 1)...(q n 1) 2 n 1
y n
(2n 1)!
(q n 1)...(q n) 2 n
y n
(2n)!
6.
2 n 1y0
Rn ( x)
q(q 1)...(q n)
(n 1)!
7.
• Формула Стирлинга представляет собой среднееарифметическое первой и второй
интерполяционных формул Гаусса:
y 1 y0 q 2 2
q (q 2 12 ) 3 y 2 3 y 1
Pn ( x) y0 q
y 1
2!
2
3!
2
q 2 (q 2 12 ) 4
y 2
4!
2 n 1 y n 2 n 1 y ( n 1)
2
q (q 2 12 )(q 2 22 )...(q 2 (n 1) 2 )
(2n)!
q 2 (q 2 12 )(q 2 22 )...(q 2 (n 1) 2 ) 2 n
y n
(2n)!
8.
2n 22n 2
y
y n
2 n 1
n 1
Rn ( x) h
q(q 2 12 )...(q 2 n2 )
2(2n 1)!
9.
• Формула Бесселя имеет вид:y0 y 1
q (q 1) 2 y 1 2 y0
Pn ( x)
(q 1/ 2) y0
2
2!
2
(q 1/ 2)q(q 1) 3
q( q 1)( q 1)( q 2) 4 y 2 4 y 1
y 1
...
3!
4!
2
2n
2n
q (q 1)(q 1)(q 2)(q 2)...(q n)(q n 1) y n y ( n 1)
(2n)!
2
(q 1/ 2)q(q 1)( q 1)( q 2)( q 2)...( q n)(q n 1) 2 n 1
y n
(2n 1)!
10.
2 n 22 n 2
y
y n
2 n 1
n 1
Rn ( x) h
q(q 2 12 )...(q 2 n2 )(q n 1)
2(2n 1)!
11.
• Формула Стирлинга применяется дляинтерполирования при значениях q, близких к 0. на
q 0, 25
практике ее используют при
12.
Формула Бесселя используется дляинтерполирования при значениях q, близких к 0,5.
Практически она используется при 0.25 q 0.75
13.
• В том случае, когда q = 0.5, формула Бесселя можетбыть переписана в виде:
y0 y 1 1 y 1 y0
3 y 2 y 1
Pn ( x)
...
2
8
2
128
2
2
2
(1 3 5...(2n 1))
( 1)
2n
2 (2n)!
2
n
4
2 n y n 2 n y ( n 1)
2
4
.
- формула интерполирования на середину.
14.
Rn ( x) ( 1)n 1 2 n 2
h
(1 3 5...(2n 1))
2 n 2
2
(2n 2)!
2
15.
• Сплайны.• кубические сплайн-функции — это
специальным образом построенные многочлены
третьей степени.
16.
• Они представляют собой некоторуюматематическую модель гибкого тонкого
стержня.
• Если закрепить его в двух соседних узлах
интерполяции с заданными углами наклонов,
то между точками закрепления этот стержень
примет некоторую форму.
17.
18.
• Пусть форма этого стержня определяется функциейy S ( x)
• между каждой парой соседних узлов интерполяции
функция S(х) является многочленом степени не выше
третьей.
19.
• Запишем ее в видеS ( x) Si ( x) ai bi ( x xi 1) ci ( x xi 1)2 di ( x xi 1)3
xi 1 x xi
20.
• Для определения коэффициентов на всехэлементарных отрезках необходимо
получить 4n уравнений.
21.
Si ( xi 1 ) ai yi 1 ,Si ( xi ) ai bi h ci h2 di h3 yi , (hi xi xi 1 )
Si ( x) bi 2ci ( x xi 1 ) 3di ( x xi 1 ) 2 ,
Si ( x) 2ci 6di ( x xi 1 ),





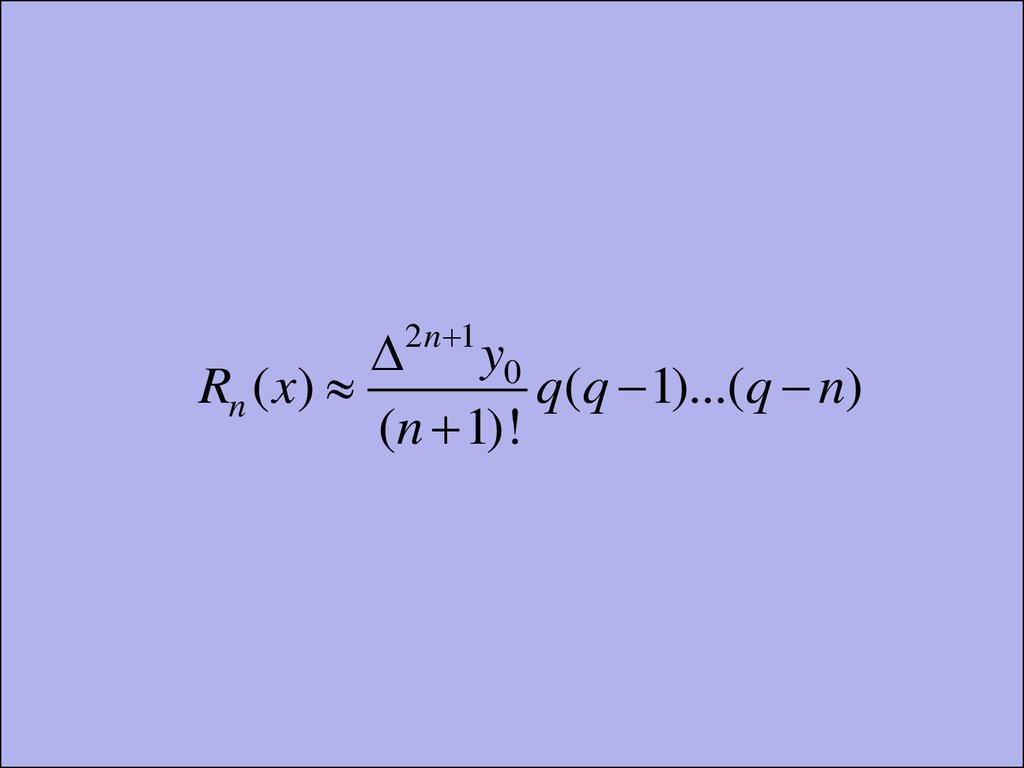















 Математика
Математика








