Похожие презентации:
Термодинамика. Лекция № 12
1.
ЛЕКЦИЯ № 12.Термодинамика.
163
1
2.
ВОПРОСЫ34. Термодинамика. Основное
уравнение молекулярнокинетической теории.
35. Первое начало термодинамики и
его применение к изопроцессам.
Уравнение Пуссона.
Работа в политропическом процессе.
36. Статистическая система и
статистический ансамбль.
Статистический вес.
163
2
3.
Вопрос № 34.Термодинамика.
Основное уравнение молекулярнокинетической теории.
Термодинамическая температура.
163
3
4.
Предварительные сведенияСтатистическая физика – раздел
физики, посвящённый изучению
свойств макроскопических тел,
исходя из свойств образующих тело
частиц и взаимодействий между
ними.
163
4
5.
Термодинамика изучает свойствамакроскопических тел и
протекающие в них процессы, не
вдаваясь в микроскопическую
природу тел.
Макроскопическое тело – тело,
состоящее из большого числа
частиц.
163
5
6.
Статистическая система – системаиз большого числа частиц.
Статистический ансамбль – система
из большого числа статистических
систем с одинаковыми
макропараметрами.
163
6
7.
Элементы термодинамикиТермодинамическая система –
совокупность макроскопических тел,
которые могут обмениваться
энергией между собой и с внешней
средой.
Здесь не описывают систему через
каждую частицу, а характеризуют её
через параметры состояния:
температуру, давление, объём,
плотность, массу и т.д.
163
7
8.
Если система не обмениваетсяэнергией с внешней средой, то она
называется замкнутой или
изолированной.
Неравновесное состояние –
состояние, в котором хотя бы один
из параметров не имеет
определённого значения.
Тепловое равновесие – равенство
температур всех частей системы.
163
8
9.
Равновесное состояние – состояниев котором все параметры состояния
имеют определённые значения, не
изменяющиеся с течением времени.
Термодинамический процесс –
переход системы из одного
состояния в другое.
Квазистатический процесс –
бесконечно медленный процесс,
состоящий из последовательности
равновесных состояний.
163
9
10.
Физические величины:Количество вещества (ν) – число
молей;
Моль - количество вещества,
содержащее число Авогадро частиц
(NA = 6,02213 · 1023 моль–1);
Объём (V, м3);
Давление (p, Па);
Температура (T, Кельвин).
163
10
11.
Статистическая физика описываеткаждую частицу для описания всей
системы, если частиц N, то получим
N * (3коорд + 3скор + 3вращ) уравнений.
Например, в 1 см3 воздуха при
t = 20°С и атмосферном давлении
содержится порядка 3 * 1019
молекул. Следовательно, для
описания этой системы необходимо
27 * 1019 уравнений.
163
11
12.
Термодинамика же оперируетсредними значениями, которые
выражаются в параметрах
состояния: объём (V, м3), давление
(p, Па), температура (T, К). При
огромном числе частиц не будет
заметной разница для каких-либо
частиц в скорости или
расположении.
163
12
13.
Уравнение состояния – этосоотношение, определяющее связь
между параметрами состояния
какого-либо тела.
Идеальный газ – газ,
взаимодействием между молекулами
которого можно пренебречь
(справедливо, когда расстояния
между молекулами много больше
размеров самих молекул).
163
13
14.
Уравнение состояния идеальногогаза
(уравнение МенделееваКлапейрона)
m
pV RT νRT
M
163
14
15.
R = k * NА = 8,31 Дж/моль*К –универсальная газовая постоянная,
k = 1,38 * 10–23 Дж/К – постоянная
Больцмана.
Если использовать концентрацию
(n = N/V), то можно записать
уравнение состояния в следующем
виде
p = nkT.
163
15
16.
Температура – количественнаяхарактеристика внутренней энергии
тела. Эта энергия не относится к
механической энергии.
m0
3
E0 kT
2
2
2
ср.кв.
ср.кв. – средне квадратичная
скорость молекулы, m0 – масса
молекулы.
163
16
17.
С учётом этого выражения можнополучить основное уравнение
молекулярно-кинетической теории
1
2
p nm0 ср.кв.
3
163
17
18.
Температуру тела определяют путёмсравнения с температурой другого
тела или через другие параметры,
которые зависят от температуры.
163
18
19.
Термодинамическая температура –температура определяющая
внутреннюю энергию тела. Если
энергии в молекулах нет, то и
термодинамическая температура
равна нулю. По термодинамической
шкале или по абсолютной шкале это
0 Кельвина (0 К = – 273,15 °С).
163
19
20.
ШкалаЦельсия
Шкала
Кельвина
100°C
373,15 K
0°C
273,15 K
0K
-273,15°C
163
20
21.
16321
22.
35. Первое начало термодинамики иего применение к изопроцессам.
Уравнение Пуссона. Уравнение
политропы.
Работа в политропическом процессе.
163
22
23.
Температура определяетвнутреннюю энергию тела. Эта
энергия слагается из кинетической
энергии поступательного и
вращательного движения молекул,
кинетической и потенциальной
энергии колебательного движения
атомов в молекулах, потенциальной
энергии взаимодействия между
молекулами и внутримолекулярной
энергии.
163
23
24.
Внутреннюю энергию можноизменить двумя способами:
передавая телу некоторое
количество теплоты dQ
(теплопередача) или совершая над
телом работу dA/
ΔU = dQ + dA/
или
dQ = ΔU – dA/ = ΔU + dA.
dA – работа тела при расширении.
163
24
25.
Первое начало термодинамики:количество теплоты, сообщённое
систем, идёт на приращение
внутренней энергии системы и на
совершение системой работы над
внешними телами.
dQ = ΔU + dA.
163
25
26.
Политропический процесс – процессс постоянной теплоёмкостью.
Политропический процесс
описывается уравнением политропы
pV const, TV
n
n 1
const,
1 n
p T const.
n
Здесь n – показатель политропы
n
C Cp
C CV
, C
163
nCV C p
n 1
.
26
27.
С – теплоёмкость 1 моля вещества,Сp – теплоёмкость 1 моля вещества
при постоянном давлении, СV –
теплоёмкость 1 моля вещества при
постоянном объёме.
Уравнение политропы отличается от
уравнение Менделеева-Клапейрона
тем, что вместо трёх параметров
используется только два.
163
27
28.
n0
C
Сp
Изохорический
процесс
СV
Изотермический
процесс
1
Адиабатический
процесс
γ
0
Изобарический
процесс
163
28
29.
Изобарический процесс – процесспри постоянном давлении.
Изохорический процесс – процесс
при постоянном объёме.
Изотермический процесс – процесс
при постоянной температуре.
Адиабатический процесс – процесс в
теплоизолированный (без
теплообмена с окружающей средой).
163
29
30.
Работа в случае изобарическогопроцесса:
A = pΔV.
В случае изохорического процесса
нет изменения объёма, значит нет
перемещения, значит работа будет
равняться нулю: A = 0.
163
30
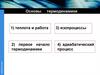
31.
Для вычисления работы вадиабатическом процессе
представим зависимость давления
от объёма с помощью уравнения
Пуассона (политропический процесс
без теплообмена)
γ
p1V1
γ
const
pV const, p V γ
V
V
γ
.
p1, V1 – начальные параметры.
163
31
32.
p1V1 V1A
1
n - 1 V2
163
n 1
32
33.
В случае изотермического процессаполучим следующее выражение
V2
V2
dV
A p V dV p1V1
V
V1
V1
V2
dV
V2
p1V1
p1V1 ln V V
1
V
V1
V2
p1V1 ln
V1
163
33
34.
16334
35.
Вопрос № 36.Статистическая система и
статистический ансамбль.
Статистический вес.
Энтропия.
Изменение энтропии идеального
газа при изопроцессах.
163
35
36.
Статистическая система – системаиз большого числа частиц.
Статистический ансамбль – система
из большого числа статистических
систем с одинаковыми
макропараметрами.
163
36
37.
Рассмотрим некоторыйтермодинамический процесс.
Система перешла из состояния «1» в
состояние «2». Если мы имеем дело
с равновесным (квазистатическим)
процессом, то при изменении
направления равновесного процесса
система будет проходить через те же
равновесные состояния. Поэтому
равновесные процессы называют
обратимыми.
163
37
38.
Необратимый процесс(неравновесный) – процесс, в
котором система не может вернуться
в исходное состояние тем же путём.
p
2
1
V
163
38
39.
О направлении процесса не всегдавозможно говорить, используя
только термодинамические
параметры. Приведём пример.
Имеется изолированная система из
двух частей. Температуры в частях
одинаковы, но давления разные.
Если части объединить, то давления
будут выравниваться. В обратном
направлении процесс не пойдёт,
хотя теоретически это возможно.
163
39
40.
T1 = T2,p1 > p2.
T1 = T2,
p1 = p2.
163
40
41.
Теоретически, это событиевозможно, но вероятность этого
события практически равна нулю.
Отсюда делаем вывод: для
определения процесса в
изолированной термодинамической
системе (т/д), нужно дать
вероятность различных состояний
этой системы.
163
41
42.
Рассмотрим ящик с двумя отделами,в котором лежит один камень или
два, или три и т.д. Посчитаем
количество вариантов расположения
камней и вероятность
осуществления конкретного
расположения.
163
42
43.
Один камень (n = 1),2 способа (N = 21), 2 * ½ = 1.
n = 2, N = 4 = 22,
¼ + ¼ + ¼ + ¼ = 1.
n = 3, N = 8 = 23,
2 * ⅛ + 6 * ⅛ = 1.
163
43
44.
Пять камней (n = 5),N = 32 = 25,
1 = (2 + 10 + 20) * 1/32.
163
44
45.
На рисунках представлены всевозможные микросостояния.
Согласно эргодической гипотезе все
микросостояния равновероятны.
Однако, они относятся к разным
макросостояниям. Каждое
макросостояние может быть
реализовано различными
микросостояниями.
163
45
46.
Состояние термодинамическойсистемы также может быть задано с
помощью макроскопических
параметров (T, p, V). Именно в этом
случае говорят о макросостоянии.
Если система находится в
равновесии, то параметры будут
постоянными, а макросостояние
неизменяющимся.
163
46
47.
Но для разных макросостоянийразное число микросостояний (не
важно какая именно частица
находится в данном месте, главное
что находится), которые могут
меняться, не изменяя
макросостояния. Теоретически могут
быть все макросостояния, но
вероятность некоторых стремится к
0, а некоторых к 1.
163
47
48.
Число различных микросостояний,посредством которых
осуществляется данное
макросостояние, называется
статистическим весом
макросостояния – Ω.
Для одного моля кислорода
(p = 1 атм, t = 20°C)
10
163
6,5*10
24
48
49.
Как видно, число огромное.Энтропия – характеристика
вероятности состояний (или
характеристика числа состояний
системы):
σ ln , S k ln
формула Больцмана.
Для моля кислорода
σ = 1,5 * 1025, S = 200 Дж/К.
163
49
50.
Энтропия – функция состояния,следовательно, её можно выразить
через параметры состояния:
S ν CV ln T R ln V S0 ,
T2
V2
S ν CV ln R ln
T1
V1
S0 – константа.
163
50
51.
Если процесс обратимый, тоdS = dQ/T.
Свойства энтропии
1) В ходе необратимого процесса
энтропия изолированной системы
возрастает;
2) Энтропия изолированной системы,
находящейся в равновесном
состоянии, максимальна.
163
51
52.
Практичнее вычислять не энтропию,а её изменение. Изменение
энтропии:
Изобарический процесс
T2
V2
S ν CV ln R ln
T1
V1
163
52
53.
Изотермический процессV2
S νR ln
V1
Изохорический процесс
T2
S νCV ln
T1
Адиабатический процесс
ΔS = 0.
163
53
54.
16354
55.
ЛЕКЦИЯ № 13.Теорема Карно
Функции распределения
163
55
56.
ВОПРОСЫ37. Второе начало термодинамики.
Тепловая смерть вселенной. Третье
начало термодинамики. Теорема
Карно.
38. Функция распределения
Максвелла.
39. Барометрическая формула
Больцмана. Распределение Гиббса.
163
56
57.
37. Второе начало термодинамики.Тепловая смерть вселенной. Третье
начало термодинамики. Цикл Карно,
его КПД для идеального газа.
Теорема Карно.
163
57
58.
Элементы теории вероятностиВероятность – отношение событий с
i-м исходом Ni к полному числу
испытаний N, при N стремящемся к
бесконечности
Ni
p lim
N N
Пример: Вероятность выпадения «6»
при бросании кубика равна 1/6.
163
58
59.
Если события зависимы(вероятность выпадения
и «1» и «6»),
то вероятности умножаются,
1/6 * 1/6.
Если события независимы
(вероятность выпадения
или «1» или «6»),
то вероятности складываются,
1/6 + 1/6.
163
59
60.
Эргодичность (эргодическаягипотеза) – все вероятности
появления того или иного события
равны.
То есть, если бросить кубик 6000
раз, то все числа выпадут по 1000
раз.
163
60
61.
Однако, при бросании 6000 разкубика, грань «6» выпадет не 1000
раз. Это число будет или меньше
или больше из-за флуктуаций.
Флуктуации – случайные отклонения
от наиболее вероятного
распределения.
Типичные значения флуктуаций
характеризуются следующей
величиной
σ N
163
61
62.
Если произвести 600 бросанийкубика, то число «6» выпадет
100 100 100 10
раз.
В 1 см3 воздуха содержится 2,7·1019
молекул, значит мы там обнаружим
2,7 10 5,2 10
19
9
молекул
163
62
63.
Очевидно, что флуктуации темнезаметнее, чем большее число
испытаний
σ
1
lim
lim
0
N N
N N
163
63
64.
Второе начало термодинамики –энтропия изолированной
термодинамической системы может
только возрастать либо по
достижении максимального
значения, оставаться постоянной
(убывать не может).
Это начало по другому называют
законом возрастания энтропии.
163
64
65.
Если процесс обратимый, тоэнтропия не изменяется
dQ
dS
, dS 0.
T
Если процесс необратимый, то
dQ
dS
, dS 0.
T
Эти уравнения можно объединить
(неравенство Клаузиуса)
dQ
dS
, dS 0.
T
163
65
66.
Исходя из законов термодинамики(второе начало термодинамики)
Клаузиус пришёл к выводу, что рано
или поздно установится равновесие.
Всякие процессы прекратятся. Этот
вывод известен как тепловая смерть
вселенной.
Но на данный момент вселенную не
рассматривают как замкнутую
систему, следовательно, второе
начало здесь не применимо.
163
66
67.
Тепловая смерть вселенной нереализуема ещё по одной причине,
из-за флуктуаций. Вселенная
огромна, следовательно, флуктуации
принимают очень большие значения,
хотя, на общем фоне они не будут
заметны.
163
67
68.
Третье начало термодинамики(теорема Нернста) – энтропия
любого тела стремится к нулю при
стремлении к нулю температуры
(недостижимость абсолютного нуля).
lim S 0
T 0
163
68
69.
Теорема Карно – коэффициентполезного действия всех обратимых
машин, работающих в идентичных
условиях (т.е. при одной и той же
температуре нагревателя и
холодильника), одинаков и
определяется только температурами
нагревателя и холодильника.
163
69
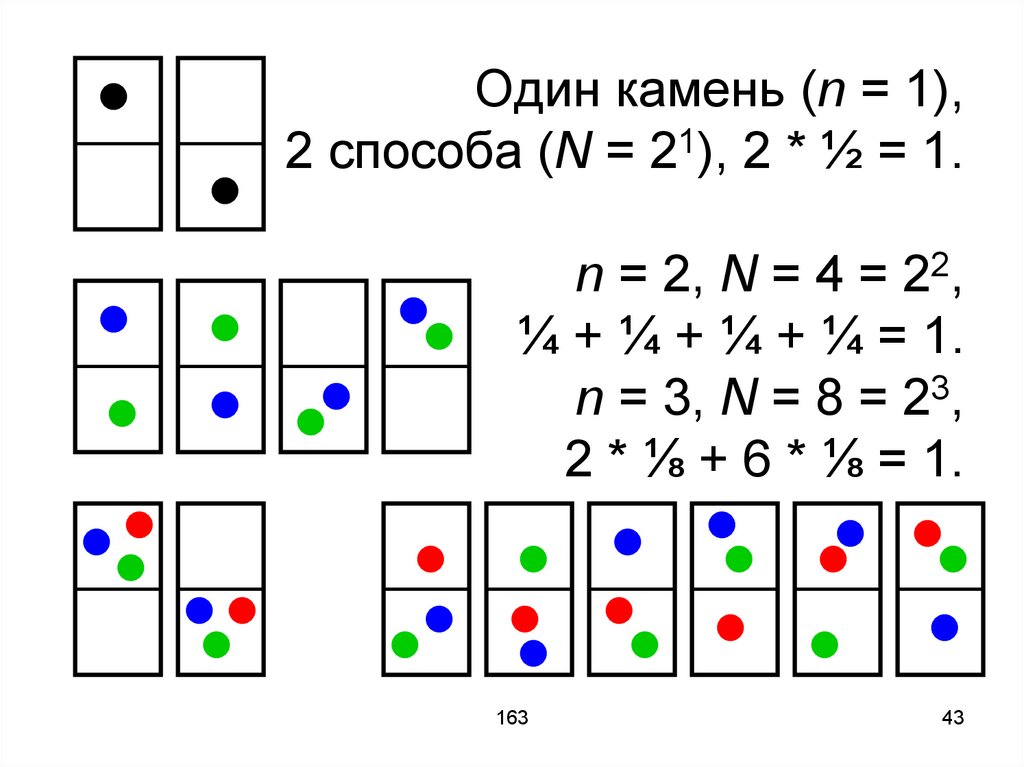
70.
Цикл Карно – цикл, состоящий издвух изотермических процессов и
двух адиабатических процессов.
Этот цикл можно назвать
изоэнтропийным – это обратимый
цикл, энтропия в этом цикле не
изменяется.
163
70
71.
PT
1
Qн
2
4
3
V
163
1
2
4
3
Qх
S
71
72.
На участке 1-2 рабочее телополучает энергию Qн от нагревателя
с температурой T1 (Tн).
На участке 2-3 тело продолжает
расширяться и совершать работу.
На участке 3-4 рабочее тело отдаёт
часть тепла холодильнику Qх с
температурой T2 (Tх).
На участке 4-1 тело сжимается и
переходит в исходное состояние.
163
72
73.
Коэффициент полезного действия(КПД) для реальной тепловой
машины и для идеальной тепловой
машины
Qн Qх
Tн Tх
η
, η
.
Qн
Tн
163
73
74.
16374
75.
38. Функция распределенияМаксвелла. Наиболее вероятная,
средняя и среднеквадратичная
скорости молекул.
163
75
76.
Распределение МаксвеллаРаспределение по составляющей
скорости – плотность вероятности
для распределения частиц по ʋx:
1
2
m0
m0
φ x
exp
2 πkT
2kT
2
x
здесь m0 – масса молекулы,
k = 1,38 · 10–23 Дж/К постоянная
Больцмана.
163
76
77.
φ(ʋx)1,2
1
0,8
0,6
0,4
ʋx
0,2
0
0
5
10
15
20
25
30
35
40
45
ʋx ʋx+dʋx
163
77
78.
Функции φ(ʋx), φ(ʋy), φ(ʋz)статистически независимы, поэтому
можно их считать равными друг
другу.
Для получения распределение по
вектору скорости воспользуемся
формулой
2
2
x
2
y
163
2
z
78
79.
Распределение по вектору скоростиf φ x φ y φ z φ x
3
3
2
m0
m0
exp
2πkT
2kT
2
163
79
80.
Распределение по модулю скорости(распределение Максвелла)
2
F 4 π f
3
2
m0
m0
4 π
exp
2 πkT
2kT
2
163
2
80
81.
16381
82.
Функция F(ʋ) – функция вероятности.Именно, F(ʋ)dʋ – есть вероятность
найти молекулу со скоростью в
интервале (ʋ, ʋ + dʋ). Если
домножить на число молекул N, то
получим число молекул,
обладающих скоростью в интервале
(ʋ, ʋ + dʋ). Полная вероятность
F d 1
0
163
82
83.
Наивероятнейшая скорость(находится из производной функции
по скорости dF(ʋ)/dʋ = 0)
2kT
вер
m0
Средняя скорость
8kT
F d
πm0
0
Среднеквадратичная скорость
ср.кв.
3kT
F d
m0
0
2
163
83
84.
16384
85.
Вопрос № 39.Барометрическая формула
Больцмана. Распределение Гиббса.
163
85
86.
Барометрическая формула(формула Больцмана)
Mgh
p p0 exp
,
RT
Mgh
n n0 exp
.
RT
163
86
87.
Здесь p, n – давление иконцентрация на высоте h, p0, n0 –
давление и концентрация на уровне
моря (h = 0), T – температура газа,
g = 9,80667 м/с2 – ускорение
свободного падения, M – молярная
масса, R = 8,31 Дж/моль*К –
универсальная газовая постоянная.
163
87
88.
Распределение ГиббсаДля полного описания состояния
термодинамического равновесия
физической системы (любого тела)
используется распределение
Гиббса, которое позволяет
определить все макроскопические
параметры системы, т. е. найти
уравнение состояния, и флуктуации.
163
88
89.
В классической механике состояниесистемы N частиц полностью задано
6N – переменными (импульсами и
координатами: dx,dy,dz,dpx,dpy,dpz).
Значения этих переменных можно
откладывать по осям абстрактной
6N-мерной системы координат.
Такое пространство называют
фазовым, в котором каждому
состоянию системы соответствует
одна точка.
163
89
90.
В квантовомеханическомраспределении производят
распределение по уровням энергии
εi.
Уровни энергии бывают кратными
(вырожденными) – если существует
несколько состояний молекулы с тем
же значением энергии,
отличающихся друг от друга
значениями других физических
величин.
163
90
91.
Простые (невырожденные) – всезначения энергии разные.
Будем полагать все уровни
невырожденными.
Найдём такое распределение
частиц, которому соответствует
максимальное значение
статистического веса Ω и,
следовательно, максимальное
значение энтропии.
163
91
92.
Учтём также следующие условия.Постоянство количество частиц:
N1 + N2 + … + Nm = N = const,
Постоянство энергии:
N1 ε1+ N2 ε2 + … + Nm εm = E = const,
здесь Ni – число частиц в i-м
состоянии, εi – энергия частиц в i-м
микросостоянии.
163
92
93.
Пропуская вывод, запишем данноераспределение частиц по энергиям
Ni N 0exp ε i kT
Это распределение МаксвеллаБольцмана
или каноническое распределение
Гиббса.
Здесь N0 – число частиц в
микросостоянии где ε = 0, N i –
среднее число частиц в состоянии с
энергией εi.
163
93
94.
Функции распределения ФермиДирака и Бозе-Эйнштейна163
94
95.
Согласно современной квантовоймеханике все элементарные и
сложные частицы разделяются на
два класса:
163
95
96.
1-й класс: электроны, протоны,нейтроны и все частицы с
полуцелым спином. Эти частицы
подчиняются статистике ФермиДирака. Они называются
фермионами.
2-й класс: фотоны, π- и К-мезоны и
все частицы с целым спином. Они
подчиняются статистике БозеЭйнштейна и называются бозонами.
163
96
97.
В статистике Ферми-Диракапринимается, что в каждом
квантовом состоянии может
находиться не более одной частицы.
Бозоны в любом квантовом
состоянии могут находиться в любом
количестве.
Рассмотрим примеры
распределения.
163
97
98.
Распределение Больцмана(классические частицы). 2 частицы в
3-х разных варианта (три ячейки). 9
возможных вариантов, вероятность
одного способа (состояния) 1/9.
А
А
Б
Б
А
Б
Б
А
Б
АБ
Б
А
163
А
АБ
АБ
98
99.
Распределение Бозе-Эйнштейна.2 частицы в 3-х разных варианта (три
ячейки). 6 возможных вариантов,
вероятность одного способа
(состояния) 1/6.
●
●
●
163
99
100.
Распределение Ферми-Дирака.2 частицы в 3-х разных варианта (три
ячейки). 3 возможных варианта,
вероятность одного способа
(состояния) 1/3.
163
100
101.
Число способов, которыми можнораспределить Ni число частиц по Zi
квантовым состояниям i-го слоя,
будет:
Фермионы
Zi!
Gi
Ni ! Z i Ni !
Бозоны
Z i N i 1 !
Gi
N i ! Z i 1 !
163
101
102.
Законы распределенияФермионы
Ni
1
ni
Zi
exp ε i μ kT 1
Бозоны
Ni
1
ni
Zi
exp ε i μ kT 1
ni – среднее число частиц
приходящееся на одно квантовое
состояние.
163
102
103.
μ – химический потенциал,определяется из условия
нормировки
Zi
Zi ni exp ε μ kT 1 N
i
здесь N – полное число частиц.
163
103
104.
СправкаЭлементы комбинаторики
Перестановка
Pn n!
Размещения из n по m (n ≥ m)
n!
A
n m !
m
n
Сочетания из n по m (n ≥ m)
n!
C
т! n m !
m
n
163
104
105.
163105
106.
Вопрос № 40.Степени свободы. Внутренняя
энергия системы. Теплоёмкость,
уравнение Майера. Теорема о
равнораспределении энергии по
степеням свободы. Недостаточность
классического представления о
теплоёмкости газов.
163
106
107.
Закон равнораспределенияБольцмана: на каждую степень
свободы молекулы приходится в
среднем одинаковая кинетическая
энергия, равная ½ kT.
163
107
108.
Средняя энергия молекулыE0 = i/2 kT,
i = nпост + nвр + 2 nколеб – число
степеней свободы – наименьшее
число независимых координат,
которое необходимо для
однозначного задания положения
молекулы в пространстве.
163
108
109.
Внутренняя энергия идеального газаi
i
U N E0 NkT νRT
2
2
Теплоёмкость молярная – это
количество энергии, необходимое
для нагревания одного моля
вещества на один градус кельвина.
163
109
110.
Теплоёмкость молярная припостоянном объёме
U
i
CV
R
νT 2
Теплоёмкость молярная при
постоянном давлении
i 2
Cp
R
2
Показатель адиабаты
163
Cp i 2
γ
CV
i
110
111.
Уравнение МайераC p CV R
Теплоёмкость одного моля при
постоянном давлении больше
теплоёмкости одного моля при
постоянном объёме на величину R.
Физический смысл R – это работа
одного моля идеального газа при
нагревании на один градус кельвина.
163
111
112.
Реальная теплоёмкость отличаетсяот теоретических расчётов. Более
точные значения даёт квантовая
теория.
Поступательная энергия не
квантуется, поэтому три
поступательные степени свободы
присутствуют всегда, при любой
температуре.
163
112
113.
Вращательная и колебательнаяэнергии квантуются. Квант
вращательной энергии много
меньше кванта колебательной
энергии. Поэтому при разных
температурах одна и та же молекула
обладает разным количеством
степеней свободы. Благодаря
распределению по скоростям у
разных молекул разное количество
степеней свободы.
163
113
114.
2ΔEкол
ΔEвр
1
163
114
115.
163115
116.
Удельная теплоёмкость Н2, Ср2500
Ср*0,01, кДж/кг*К
2000
1500
1000
500
0
0
1000
2000
3000
4000
5000
6000
7000
T, К
163
116
117.
Удельная теплоём кость Н2, Ср1500
1480
Ср*0,01, кДж/кг*К
1460
1440
1420
1400
1380
1360
1340
1320
1300
0
200
400
600
800
1000
T, К
163
117
118.
163118
119.
ЛЕКЦИЯ 14.Реальные газы. Уравнение Ван-дерВаальса.
163
119
120.
ВОПРОСЫ41. Реальные газы. Уравнение Вандер-Ваальса. Изотермы Ван-дерВаальса. Критическая точка.
42. Фазы и условия равновесия фаз.
Фазовые превращения. Уравнение
Клапейрона-Клаузиуса.
43. Поверхностные явления.
Коэффициент поверхностного
натяжения. Формула Лапласа.
Смачивание.
163
120
121.
Вопрос № 41.Реальные газы. Уравнение Ван-дерВаальса. Изотермы Ван-дерВаальса. Критическая точка.
163
121
122.
Уравнение состояния идеальногогаза
pV = m/M RT
описывает поведение достаточно
разреженных газов. Реально,
приходится учитывать следующие
факторы:
1) молекулы имеют некоторый
объём;
2) молекулы взаимодействуют друг с
другом.
163
122
123.
Наиболее точно описываетповедение реальных газов
уравнение Ван-дер-Ваальса:
a
p 2 V b RT ,
V
2 a
p ν 2 V νb νRT .
V
Для одного моля и для ν молей.
163
123
124.
Здесь b выражает объём молекулодного моля, a выражает силу
взаимодействия молекул.
163
124
125.
Изотермы Ван-дер-ВаальсаПолучим зависимость давления p от
объёма V при постоянной
температуре. Для удобства
перепишем уравнение Ван-дерВаальса в следующем виде.
a ab
pV pb 2 RT .
V V
163
125
126.
Продифференцируем выражениеВан-дер-Ваальса дважды (T = const)
a 2ab
dp V b p 2 3 dV 0,
V
V
a 2ab a V 2b
pэкстр 2 3
,
3
V
V
V
Vэкстр 3b.
163
126
127.
Во второй производной мы пришли кзначению критического объёма
(экстремум функции)
Vк = 3b.
Используя это выражение получим
значения критического объёма и
критической температуры
pк = a/27b2, Tк = 8a/27bR.
163
127
128.
В точке К кривая экстремумов(первая производная) сама имеет
экстремум (здесь min и max Ван-дерВаальсовской кривой изотермы
сливаются, изотерма в этой точке
горизонтальна и имеет перегиб). При
температурах, больших
температуры критической, изотермы
становятся монотонными.
163
128
129.
163129
130.
163130
131.
ppк
b
2b 3b
163
V
131
132.
Горизонтальный участок проводитсятаким образом, чтобы площади,
ограниченные кривой и
горизонтальной линией были равны.
Внутренняя энергия и энтропия газа
Ван-дер-Ваальса
ν a
U νCVT
,
V
S ν CV ln T R ln V b S0 .
2
163
132
133.
163133
134.
Вопрос № 42.Фазы и условия равновесия фаз.
Фазовые превращения. Уравнение
Клапейрона-Клаузиуса.
163
134
135.
Фазовые превращенияУравнение Ван-дер-Ваальса хорошо
описывает переход вещества из
одного агрегатного состояния в
другое – фазовое превращение.
Фаза – совокупность однородных,
одинаковых по своим свойствам
частей системы.
163
135
136.
Фазовый переход 1-го рода –переход вещества из одной фазы в
другую с поглощением или
выделением некоторого количества
теплоты, теплоёмкость меняется
скачком.
Фазовый переход 2-го рода –
переход из одной кристаллической
модификации в другую,
теплоёмкость меняется плавно.
163
136
137.
Испарение – переход жидкости в газ.Конденсация – переход газа в
жидкость.
Сублимация (возгонка) – переход
твёрдого тела в газообразное
состояние.
Плавление/отвердевание
(кристаллизация) – переход из
твёрдого состояния в
жидкое/переход из жидкого
состояния в твёрдое.
163
137
138.
Рассмотрим герметичный сосуд снекоторым количеством жидкости.
Наиболее быстрые (энергичные,
горячие) молекулы могут покинуть
жидкость и перейти в пар (газовое
состояние). При этом жидкость
охлаждается. Некоторые молекулы
из пара могут перейти в жидкость.
Жидкость при этом нагревается.
163
138
139.
Если число молекул, покинувшихжидкость равно числу молекул
вернувшихся за один и тот же
период, то говорят о
термодинамическом равновесии
жидкости с её паром, а пар
называют насыщенным.
163
139
140.
Зависимость давления насыщенногопара от температуры. Tp – тройная
точка.
p
pкр
К
Tp
Tкр
T
163
140
141.
На изотерме Ван-дер-ваальсовскогогаза процессу испарения или
конденсации соответствует
горизонтальный участок. Его
проводят так, чтобы S1 = S2.
Условие равновесия
mж Vг V y
mг V Vж x
163
141
142.
VжS1
S2
x
y
V
163
Vг
142
143.
В случае испарения или конденсациисправедливо уравнение
Клапейрона-Клаузиуса
dp S2 S1
q
dT V2 V1 T V
здесь q – теплота фазового
перехода для 1 моля.
163
143
144.
Фазовые диаграммы1) Переход из одной фазы в другую
без расслаивания на две фазы,
вещество остаётся однородным;
2) перегретая жидкость;
3) перенасыщенный пар.
163
144
145.
12
3
163
145
146.
Tp – тройная точка на фазовойдиаграмме определяет условия, при
которых могут находиться в
равновесии одновременно три фазы
вещества.
Критическая точка – точка,
соответствующая условиям, при
которых исчезают отличия между
жидкостью и её паром.
(1 бар = 105 Па ≈ 1 атм)
163
146
147.
pТв. т.
Ж
Tp
К
Газ
T
163
147
148.
163148
149.
163149
150.
163150
151.
Вопрос № 43.Поверхностные явления.
Коэффициент поверхностного
натяжения. Формула Лапласа.
Смачивание.
163
151
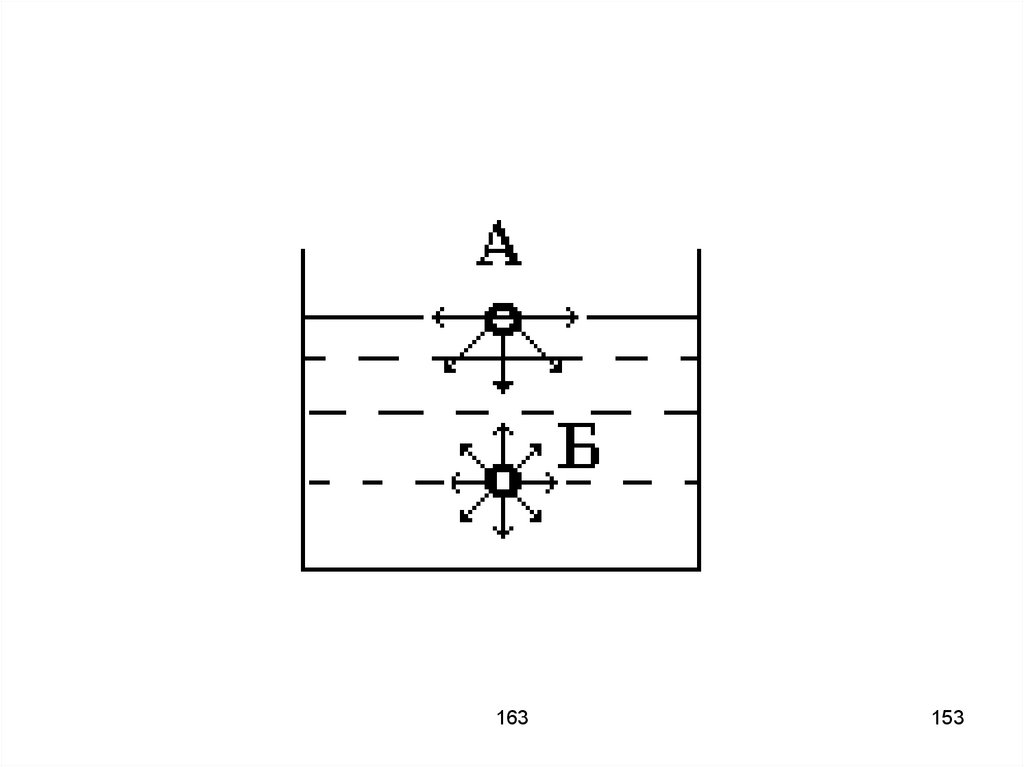
152.
Равнодействующая сил притяжения,действующих на молекулу
поверхностного слоя, направлена
внутрь жидкости. Это означает, что
такая молекула обладает некоторой
избыточной энергией. Суммарная
энергия таких молекул
пропорциональна площади
поверхности, а энергия – объёму.
163
152
153.
163153
154.
Поэтому поверхностные явленияособую роль играют, когда
отношение поверхности к объёму
велико (т.е. малые размеры и/или
малые объёмы).
Основной характеристикой является
коэффициент поверхностного
натяжения – σ, Н/м.
163
154
155.
Коэффициент поверхностногонатяжения равен отношению силы,
действующей на некоторый участок
перпендикулярно к нему, к величине
этого участка или
это отношение работы по
изменению поверхности жидкости к
изменению величины поверхности.
F
A
σ
S
163
155
156.
Формула ЛапласаВычислим добавочное давление в
пузырьке жидкости через энергию на
примере цилиндра.
Изменим радиус цилиндра r на Δr.
Изменение поверхности и
поверхностной энергии
2πr 2π r ,
W 2π σ r.
163
156
157.
Изменение объёмаπr 2πr r
2
Работа сил избыточного давления
(она же есть изменение энергии
ΔA = – ΔW)
A p V p 2πr r
W 2π σ r p 2πr r
p σ r
163
157
158.
Добавочное давление для сферы2σ
p
r
Для произвольной поверхности
1 1
p σ
r1 r2
плоскости, в которых измеряют
радиусы кривизны r1 и r2, взаимно
перпендикулярны.
163
158
159.
СмачиваниеПри рассмотрении явлений на
границе раздела различных сред
нужно рассматривать суммарную
поверхностную энергию всех трёх
тел – вся система принимает
конфигурацию, соответствующую
минимуму суммарной энергии
(поверхностной, в поле сил тяжести
и т.п.).
163
159
160.
В частности, сумма сил, в проекциина твёрдое тело, должна равняться
нулю, или, согласно рисункам,
σт,г σт,ж σж,г cosθ, σт,ж σт,г σж,г cosθ.
σж,г
σж,г
θ
σт,г
σт,ж
163
θ
σт,г
σт,ж
160
161.
Если σт,г > σж,г + σж,г, то полноесмачивание – жидкость
неограниченно растекается по
поверхности твёрдого тела.
Если σт,ж > σт,г + σт,ж, то полное
несмачивание – поверхность, по
которой жидкость граничит с
твёрдым телом, стягивается в точку,
жидкость отделяется от твёрдой
поверхности.
163
161
162.
Капиллярные явленияКапилярные явления – поднятие
жидкости (или опускание) на
определённую высоту в тонкой
трубке за счёт сил поверхностного
натяжения.
Сила тяжести компенсируется силой
натяжения
2σ
2πrσ gρhπr h
ρgr
2
163
162
163.
163163































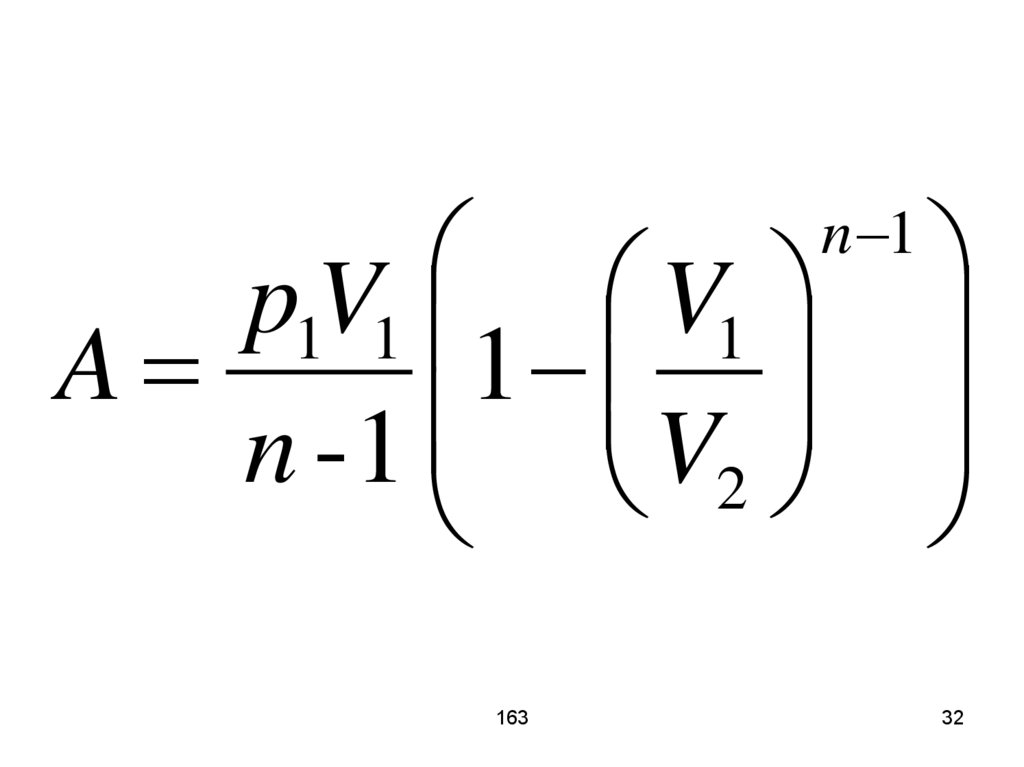
































































































































 Физика
Физика