Помехоустойчивые коды

1.

ПОМЕХОУСТОЙЧИВЫЕ
КОДЫ
1

2.

Введение
■ Подавляющее число современных систем связи работает при передаче самого
широкого спектра сообщений (от телеграфа до телевидения) в цифровом виде.
■ Из-за помех в каналах связи сбой при приеме любого элемента вызывает
искажение цифровых данных
2

3.

Стандартные протоколы обмена
информации в сетях
■ предусматривают введение обязательного поля для
размещения помехоустойчивого (корректирующего) кода.
■ Если в результате обработки принятого пакета обнаружится несоответствие
принятого и вновь вычисленного помехоустойчивого кода, с большой долей
вероятности можно утверждать, что среди принятых бит имеются ошибочные.
■ Передачу такого пакета нужно будет повторить (в расчете на случайный характер
помех).
3

4.

стандартами международных
организаций ITU-T и МОС установлено
■ , что вероятность ошибки при телеграфной связи не должна превышать 3x10-5 (на
знак),
■ а при передаче данных – 10-6 (на единичный элемент, бит).
■ На практике допустимая вероятность ошибки при передаче данных может быть
еще меньше – 10-9.
■ В то же время каналы связи (особенно проводные каналы большой протяженности
и радиоканалы) обеспечивают вероятность ошибки на уровне 10-3...10-4 даже при
использовании фазовых корректоров, регенеративных ретрансляторов и других
устройств, улучшающих качество каналов связи.
4

5.

Введение избыточности в
передаваемую информацию
является кардинальным способом снижения вероятности ошибок при
приеме является.
■ В системах передачи информации без обратной связи данный способ
реализуется в виде помехоустойчивого кодирования, многократной передачи
информации или одновременной передачи информации по нескольким
параллельно работающим каналам.
■ Помехоустойчивое кодирование доступнее, при прочих равных условиях
позволяет обойтись меньшей избыточностью и за счет этого повысить скорость
передачи информации.
5

6.

Цена введения кода
■ расширение используемой полосы частот и
■
уменьшение информационной скорости передачи.
6

7.

ИСТОРИЧЕСКИЙ
ОБЗОР
Помехоустойчивых кодов

8.

1946 г
«Работы по теории информации и кибернетике» К. Шеннона, где
■ сформулирована теорема Шеннона и
■ показано, что построение каналов связи с очень хорошими характеристиками
является дорогостоящим мероприятием, а экономически выгоднее использовать
избыточное, т.е. помехоустойчивое кодирование.
8

9.

Два направления развития теории
помехоустойчивого кодирования
■ Алгебраическое (слайды 12-18)
■ Вероятностное
Данные исследования привели к открытию алгоритмов последовательного
декодирования применительно к классу древовидных кодов, которые относятся к
классу сверточных кодов (СК), которые в свою очередь, являются дальнейшим
развитием непрерывных кодов.
9

10.

АЛГЕБРАИЧЕСКИЕ
коды

11.

1947г.
Хэммингом были построены
■ алгебраический блоковый (блочный) и
■ теория построения линейных блоковых кодов.
11

12.

1949г.
■ Абрамсон построил еще два блоковых кода
12

13.

1959 г. Хоквингейм
I960 г. Боузе и Чоудхури
предложили теорию построения линейных блоковых кодов, корректирующие
■ как независимые ошибки,
■ так и пакетные ошибки.
Эти коды получили название БЧХ-кодов.
13

14.

1960-61 гг. Рид и Соломон
независимо друг от друга разработали теорию построения линейных блоковых
кодов,
■ корректирующие пакетные ошибки
■ и группирующиеся пакеты ошибок,
■ при этом кодирование информации может быть выполнено как в двоичном поле
Галуа GF(2),
■ так и в недвоичном поле Галуа GF(2m ), m³2.
Эти коды получили название кодов Рида-Соломона или РС-кодов.
14

15.

1964 г. Прейндж
■ предложил теорию построения циклических кодов (ЦК) существенно упростивших
как алгоритм кодирования, так и алгоритм декодирования групповых кодов.
15

16.

1966 г. Файр
■ предложил теорию построения ЦК, корректирующих одиночные пакеты ошибок
произвольной кратности (длины), измеряемой в двоичных символах.
16

17.

1967 г. Форни, Блох и Зяблов
■ разработали теорию построения каскадных кодов, корректирующие
одновременно как независимые ошибки, так и пакетные ошибки.
17

18.

1967 г.
■ Витерби разработал для СК эффективный вероятностный алгоритм
декодирования, названный позднее алгоритмом Витерби (АВ).
■ С 1970 г. два направления исследований вновь стали пересекаться , в том
плане, что теорией построения СК занялись математики-алгебраисты,
представившие теорию построения СК в новом математическом изложении.
18

19.

ТЕОРИЯ
Теорема шеннона

20.

Двоичный симметричный канал (ДСК)
простейший канал с шумом
■ ДСК - это двоичный канал, по которому можно передать один из двух символов
(обычно это 0 или 1).
■ Передача не идеальна, поэтому принимающий в некоторых случаях получает другой
символ.
■ В теории связи множество проблем сводится к ДСК.
20

21.

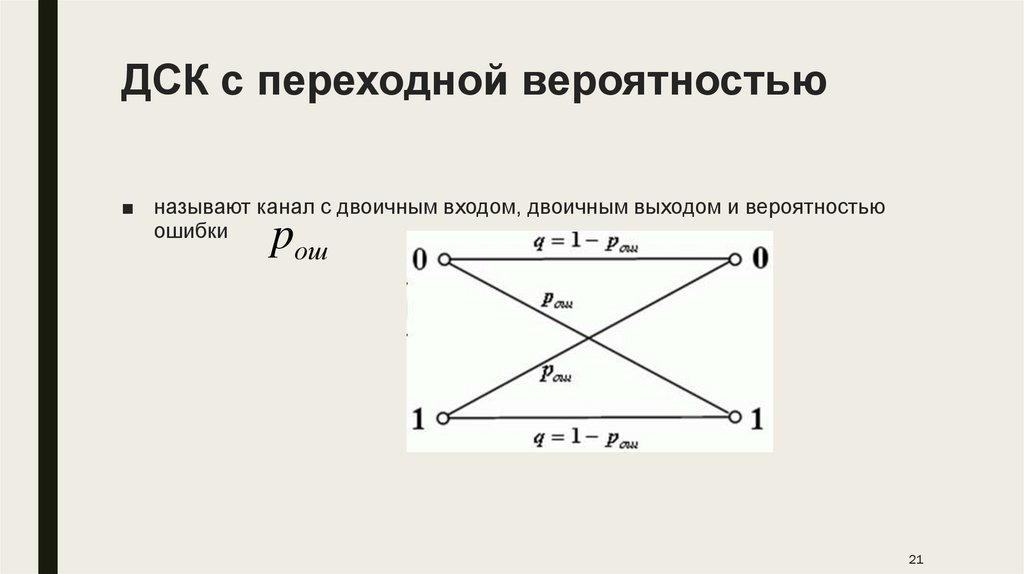
ДСК с переходной вероятностью
■ называют канал с двоичным входом, двоичным выходом и вероятностью
ошибки
pош
21

22.

ДСК с переходной вероятностью
■ канал характеризуется набором возможных входов, набором возможных
выходов и набором условных вероятностей возможных выходов при условии
возможных входов
22

23.

Пропускная способность канала
■ метрическая характеристика, показывающая соотношение предельного
количества проходящих единиц информации в единицу времени через канал
■ Наибольшая возможная в данном канале скорость передачи информации
называется его пропускной способностью.
■ Пропускная способность канала есть скорость передачи информации при
использовании «наилучших» (оптимальных) для данного канала источника,
кодера и декодера, поэтому она характеризует только канал.
23

24.

Пропускная способность ДСК
C 1 H ( pош )
24

25.

Теорема Шеннона
■ При любой производительности источника сообщений, меньшей, чем
пропускная способность канала, существует такой способ кодирования, который
позволяет обеспечить передачу всей информации, создаваемой источником
сообщений, со сколь угодно малой вероятностью ошибки;
25

26.

Теорема Шеннона
■ Не существует способа кодирования, позволяющего вести передачу
информации со сколь угодно малой вероятностью ошибки, если
производительность источника сообщений больше пропускной способности
канала
26

27.

Суть
■ Доказывается только существование искомого способа кодирования,
■ Т.е. находят среднюю вероятность ошибки по всем возможным способам
кодирования и показывают, что она может быть сделана сколь угодно малой.
■ При этом существует хотя бы один способ кодирования, для которого вероятность
ошибки меньше средней.
27

28.

H ( x) V x H ( x)
Источник создает информацию
■ со скоростью
Vxбукв в секунду и энтропией каждой буквы в среднем H (x)
Т.е. производительность равна
H ( x) Vx H ( x)
(бит/сек).
28

29.

Вспомним т. Шеннона об
эффективном кодировании
■ Сообщения, составленные из букв некоторого алфавита, можно закодировать
так, что среднее число двоичных символов на букву будет сколь угодно близко к
энтропии источника этих сообщений, но не меньше этой величины
■ И предел эффективного кодирования
H ( x) lср log 2 M
lср H (x)
29

30.

В соответствии с теоремой Шеннона
об эффективном кодировании
■ т.е., возвращаясь к слайду 6, в первом приближении можно получить, что
производительность канала равна произведению скорости букв в секунду на
среднее число двоичных символов на букву
H ( x) Vx lср
30

31.

При наличии помех пропускная
способность канала связи падает,
■ Помня что в ДСК
C 1 H ( pош )
И учитывая условие пропуска информации по каналу
H ( x) C Vk
■ Получаем пропускную способность канала
C x Vk [1 H ( Pош )]
31

32.

Требование теоремы Шеннона для
помехоустойчивого кодирования
Vx lср H ( x) Ck Vk [1 H ( Pош )]
■ Где
lср - средняя длина кодовой комбинации для записи одной буквы
■ В сравнении с эффективным кодирование это значение увеличивается до
теоретического предела (в реальности нет )
lср1
lср
1 H ( Pош )
32

33.

ОБЩИЕ ПРИНЦИПЫ
ИЗБЫТОЧНОСТИ
Помехоустойчивых кодов

34.

К основным свойствам
помехоустойчивых кодов
■ относят их способность обнаруживать и исправлять ошибки в передаче
сообщений по дискретному каналу с помехами.
■ Рассмотрим возможность их применения для обнаружения ошибок в двоичных
кодовых комбинациях.
34

35.

Предположим, что
■ исходные кодовые комбинации состоят из k символов (разрядов).
■ Всего таких комбинаций может быть N = 2k, и их называют разрешенными.
■ Идея построения помехоустойчивого кода состоит в увеличении числа разрядов в
кодовых комбинациях с k до n (n k). При этом n – k вспомогательных символов
служат для обнаружения или исправления ошибок.
■ Общее число возможных комбинаций станет равным N0 = 2n.
■ Остальные (N0 – N) = 2n – 2k комбинаций для передачи информации не
используются и называются запрещенными.
35

36.

Если на приемной стороне
установлено, что
■ принятая комбинация относится к группе разрешенных комбинаций, то она
регистрируется неискаженной.
■ В противном случае делается вывод, что принятая комбинация искажена.
■ Однако это справедливо лишь для таких помех, когда исключена возможность
перехода одних разрешенных комбинаций в другие.
36

37.

Код с проверкой на четность
■ Для его построения необходимо ко всем 2k комбинациям безызбыточного кода
добавить по одному разряду и заполнить его проверочным символом 0 или 1 по
правилу четности числа единиц.
■ Увеличивая число дополнительных разрядов, и заполняя их (по определенным
правилам) проверочными символами 0 или 1, можно усилить корректирующие
свойства кода способностью исправлять как одиночные, так и ошибки более
высокой кратности.
37

38.

Пример. Покажем возможность
обнаружения ошибок при приеме
двоичных символов.
■ Пусть k = 2. При безызбыточном двоичном кодировании в этом случае можно
образовать четыре кодовые комбинации (2k = 4): k1 = 00; k2 = 01; k3 = 10; k4 =
11.
■ Любая одиночная ошибка приведет к тому, что одна из комбинаций будет
принята за другую. Введем один дополнительный разряд, т.е. n = 3, тогда общее
количество комбинаций: 23 = 8:
■ 000; 001; 010; 011; 100; 101; 110; 111.
■ Используем как разрешенные для передачи только те четыре комбинации, число
единиц в которых четно (они подчеркнуты), а остальные четыре (с нечетным
числом единиц) будем считать запрещенными.
38

39.

000; 001; 010; 011; 100; 101; 110;
111.
■ Теперь одиночная ошибка на любой позиции разрешенной кодовой комбинации
может быть обнаружена.
■
Действительно, одиночная ошибка в разрешенной кодовой комбинации делает
общее число единиц в этой комбинации нечетным, т.е. переводит разрешенную
комбинацию в запрещенную. Это является признаком ошибки.
■ Проверяя число единиц в каждой принятой комбинации, можно установить,
какие из этих комбинаций содержат ошибку.
39

40.

КОДЫ ХЭММИНГА
Подвид Блочных линейных кодов

41.

Блочными являются коды,
■ представляющие собой последовательности длиной n кодовых элементов, из
которых m элементов являются информационными, а остальные n – m
контрольными или проверочными.
■ Блочные коды обычно обозначаются так: (n, m) — код.
■ Например, код (7, 4) — это блочный код длины 7, который содержит 4
информационных и 3 проверочных позиции.
41

42.

Принципы построения кода Хемминга
■ Существует несколько разновидностей кода Хемминга, характеризуемых
различной корректирующей способностью. Работаю все по одному принципу.
■ Избыточная часть кода строится таким образом, чтобы при декодировании
можно было бы установить не только факт наличия ошибок в принятой
комбинации, но и указать номер позиции, в которой произошла ошибка. Это
достигается за счет многократной проверки (суммирования по по модулю 2)
принятой комбинации на четность.
■ Количество проверок равно количеству k избыточных символов.
42

43.

Принципы построения кода Хемминга
■ Каждой проверкой должны охватываться часть информационных символов и
один из избыточных символов. При каждой проверке получают двоичный
контрольный символ. Если результат проверки дает четное число, то
контрольному символу присваивается значение 0, если нечетное — 1.
■ В результате всех проверок получается k-разрядное двоичное число,
составленное из контрольных символов (сумм), называемое синдромом кода и
указывающее номер искаженного символа. Для исправления ошибки достаточно
лишь изменить значение данного символа на обратное.
43

44.

Определение количества
проверочных символов для кода Х.
k (n m) log 2 (n 1),
если
d 3
44

45.

Примерами таких кодов являются
коды типа
■ (3, 1), (5, 2), (6, 3), (7, 4), (9, 5), (10, 6), (11, 7) и т.д.
■ В таких кодах значения проверочных символов и номера их позиций
устанавливаются одновременно с выбором контролируемых групп кодовой
комбинации.
45

46.

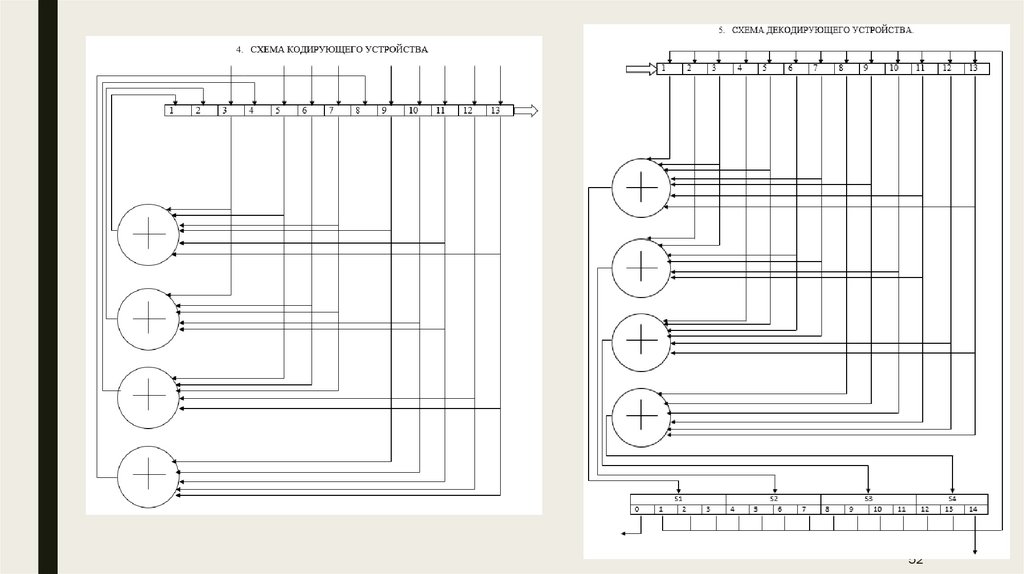
Пример
Рассмотрим с помощью табл. двоичную запись номеров разрядов 13-разрядного
числа n, используемого в коде Хэмминга (13, 9).
НО ВНАЧАЛЕ РАССМОТРИМ БАЗОВЫЕ ПОНЯТИЯ:
■ ПРОВЕРОЧНЫЕ СИМВОЛЫ
■ КОНТРОЛЬНЫЕ СУММЫ
■ СИНДРОМ ОШИБКИ
46

47.

Проверочные символы
■ С целью упрощения операций кодирования и декодирования целесообразно
выбирать такое размещение проверочных символов в кодовой комбинации, при
котором каждый из них включается в минимальное число проверяемых групп
символов.
■ В связи с этим удобно размещать контрольные символы на позициях 1, 2, 4, 8,
16, …, номера которых встречаются только в одной из проверяемых групп.
Позиции с номерами, равными степеням двойки.
Действительно, символы A1, A2, A4, A8 встречаются только в одной из проверяемых
групп. Именно на этих позициях в коде Хэмминга располагаются проверочные
символы 1, 2, 3, 4, …
Тогда информационные символы будут располагаться на позициях A3, A5, A6, A7, A9,…
47

48.

Таблица номеров разрядности
48

49.

Контрольные суммы
■ При выборе контролируемых групп символов нужно исходить из следующих правил:
■ Контрольные суммы составляются так, чтобы в сумму Si входили символы Ai кодового
слова, имеющие единицу в i — разряде двоичной записи их порядкового номера в
пределах n — разрядной кодовой комбинации.
■ в первую контрольную сумму S1 должны входить символы A1, A3, A5, A7, A9, A11, A13,
содержащие единицу в первом разряде кодовой комбинации, т.е. первой проверкой
должны быть охвачены символы с нечетными номерами.
■ контрольный бит с номером N контролирует все последующие N бит через каждые N бит,
начиная с позиции N.
49

50.

Синдром ошибки
■ Как видно из табл., в первую контрольную сумму S1 должны входить символы A1, A3, A5, A7, A9,
A11, A13, A15, содержащие единицу в первом разряде кодовой комбинации, т.е. первой
проверкой должны быть охвачены символы с нечетными номерами.
■ Второй проверкой для формирования S2 охватываются 2-я проверочная и 3-я
информационная позиции кода, и далее A6, A7, A10, A11, A14, A15, A18, A19 и т.д. каждые два
информационных разряда, через два.
■ Аналогично третьей проверкой S3 охватываются 4-я проверочная, 5-я, 6-я, 7-я
информационные позиции кода, и далее A12, A13, A14, A15, A20, A21, A22, A23 и т.д. каждые
четыре информационные разряда, через четыре.
■ Совокупность значений проверок S4 S3 S2 S1 представляет собой двоичное число, которое
называют синдром ошибки. В коде Хемминга значение синдрома ошибки эквивалентно
номеру изменённой позиции, в которой произошла одиночная ошибка, исказившая код.
50

51.

ВЫЧИСЛЕНИЕ ПРОВЕРОЧНЫХ
СИМВОЛОВ
■ Значения проверочных символов 1, 2, 3, 4 должны выбираться таким
образом, чтобы обратить в нуль контрольные суммы S1, S2, S3, S4.
51

52.

52