Похожие презентации:
Интегрирование некоторых иррациональных функций (лекция 01)
1.
§ 6. Интегрирование некоторых иррациональных функций1) Случай R x, k x , l x , m x ,... dx .
Пусть n – наименьшее кратное всех показателей k, l, m, … целые числа. Это означает, что:
n
n
n
r1 , r2 , r3 ,... ,
k
l
m
где r1, r2, r3, … – целые числа. В этом случае используют замену
переменной
x u n , dx nu n 1du .
dx
Пример. Найти
.
3
x x
В данном случае n 2 3 6 . Используем замену переменной:
x u 6 , x u 3 , 3 x u 2 , dx 6u 5 du .
Тогда получим
2.
dx6u 5 du
u 3 du
u 3 1 1 du
x 3 x u 3 u 2 6 u 1 6 u 1
3
2
du
u
u
2
6 u u 1 du 6
6
u ln u 1 C
u 1 3
2
x 3 x 6
6
6
x ln x 1 C .
2
3
ax b ax b
,m
,... dx .
2) Случай R x, k
px q px q
В этом случае используют замену переменной:
ax b
qu n b
aq bp
n
n 1
u , x
,
dx
nu
du .
n
2
n
px q
a pu
a pu
3.
3) Случайdx
.
ax bx c
Здесь необходимо рассмотреть два случая: a 0 и a 0 .
Результат интегрирования будет совершенно различный.
1
Пусть a 0 . После вынесения за знак интеграла
, интеграл
a
dx
приводится к виду
. Выделяя полный квадрат в
2
x px q
dx
подкоренном выражении, получим интеграл
,
2
p
4q p 2
x
2
4
который выражается через логарифмы.
2
4.
Пусть a 0 . После вынесения за знак интегралаинтеграл приводится к виду
dx
1
,
a
. Выделяя полный
x 2 px q
квадрат
в подкоренном
выражении, получим интеграл
4q p 2
dx
0 выражается
, который в случае
2
4
4q p 2
p
x
4
2
через арксинус.
dx
4) Случай
.
2
x ax bx c
1
В этом случае замена x приводит интеграл к виду 3.
u
5.
5) СлучайAx B
dx .
ax bx c
Интеграл после выделения в числителе производной
подкоренного выражения разбивается на два интеграла, один из
которых является интегралом от степенной функции, а второй
является интегралом вида 3.
2
ax bx c 2ax b
1
Ax B A 2ax b 2aB Ab
2a
Ax B
A 2ax b dx
2aB Ab
dx
ax 2 bx c dx 2a ax 2 bx c 2a ax 2 bx c
2
6) Случай
ax 2 bx c dx .
Выделением полного квадрата в подкоренном выражении
интеграл приводится к одному из трех следующих видов:
u 2 1du, u 2 1du, 1 u 2 du .
6.
§ 7. Интегрирование некоторых трансцендентных функцийТрансцендентными называют элементарные функции, не
являющиеся алгебраическими. Они образованы с помощью
возведения в иррациональную степень, логарифмирования,
использования
тригонометрических
и
обратных
тригонометрических операций.
Пример. Функция y ln x 2 2 – трансцендентная.
Интегралы от трансцендентных функций в общем случае не
выражаются в элементарных функциях.
1) Случай P x e ax dx , где P x – многочлен.
Интеграл вычисляется интегрированием по частям или
методом неопределенных коэффициентов. Во втором случае
результат ищут в виде
ax
ax
P
x
e
dx
Q
x
e
C, a 0 ,
где Q(x) – многочлен той же степени, что и P(x).
7.
Пример. Вычислить2x
xe
dx .
2x
2x
2x
e
e
e
1 2x
2x
xe
dx
x
dx
x
e C
2
2
2 4
Будем использовать метод неопределенных коэффициентов,
для чего положим
2x
2x
xe
dx
Ax
B
e
C.
Дифференцируя левую и правую часть этого уравнения, получим
xe 2 x Ae 2 x Ax B 2e 2 x или x A 2 B 2 Ax .
Так как левая часть этого уравнения должна быть равна правой
части при любом x, необходимо положить
A 2B 0 , 2 A 1,
1
1
откуда получим A , B .
2
4
Следовательно, интеграл равен
1 2x
1
2x
xe
dx
x
e C .
4
2
8.
2) СлучайP x cos xdx, P x sin xdx , где P x – многочлен.
Интеграл вычисляется интегрированием
методом неопределенных коэффициентов.
Пример. Вычислить x cos xdx .
по
частям
или
Интегрируя по частям, получим
u x , du dx , cos xdx dv , sin x v , udv uv vdu
x cos xdx x sin x sin xdx x sin x cos x C .
Используя метод неопределенных коэффициентов, положим
x cos xdx Ax B sin x Ex D cos x C .
Дифференцируя левую и правую часть этого уравнения, получим
x cos x A sin x Ax B cos x E cos x Ex D sin x
или
x cos x A Ex D sin x Ax B E cos x .
Так как левая часть этого уравнения должна быть равна правой
части при любом x, необходимо положить
9.
откуда получимA 1, B E 0, A D 1 .
Следовательно, интеграл равен
x cos xdx x sin x cos x C
3) Случай
R sin x, cos x dx .
Здесь используется тригонометрическая подстановка
x
1 u2
2u
2du
tg u , sin x
, cos x
, dx
.
2
2
2
2
1 u
1 u
1 u
dx
Пример. Вычислить интеграл
.
3 5 cos x
Используя тригонометрическую подстановку, получим
dx
2du
du
1 1
1
dt
3 5 cos x
2
2
4 2 u 2 u
4 u
1 u
2
1 u 3 5
2
1 u
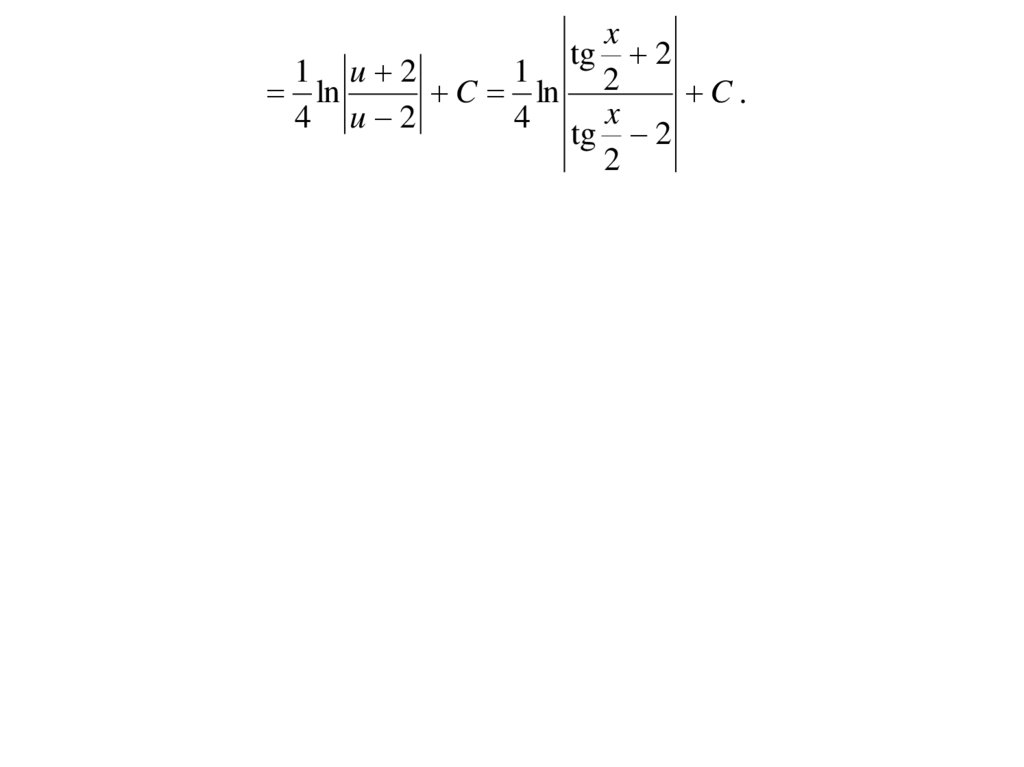
10.
xtg 2
1 u 2
1
ln
C ln 2
C.
x
4 u 2
4 tg 2
2

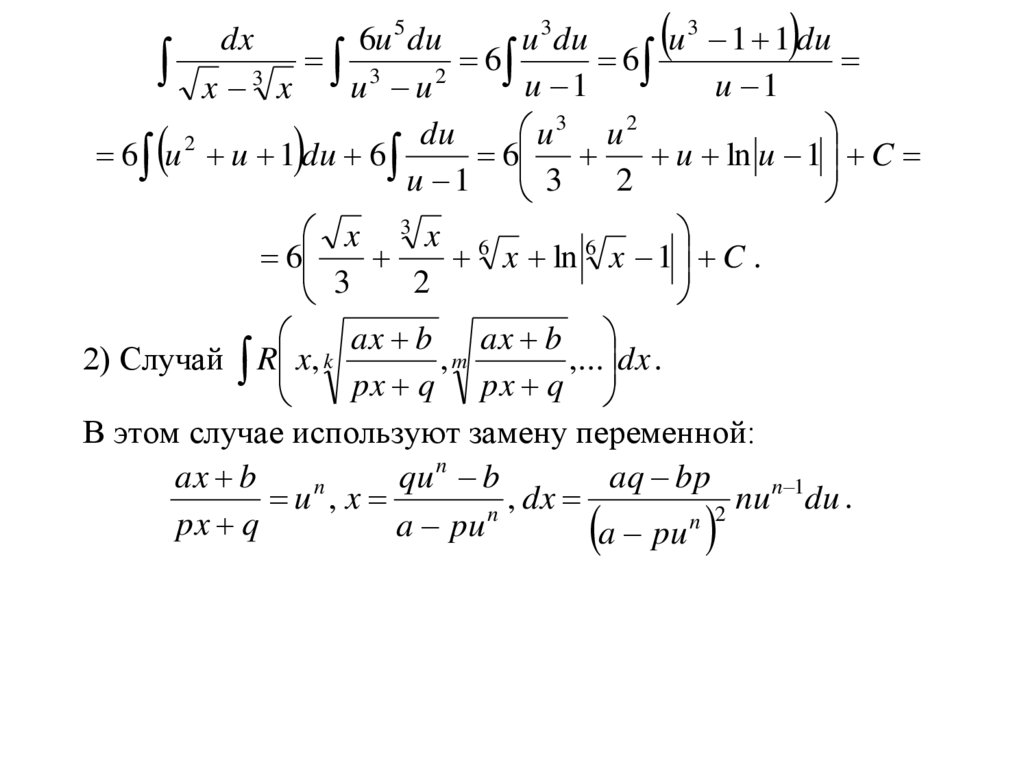







 Математика
Математика








