Случайные погрешности

1.

Случайные погрешности
Случайные погрешности неопределенны по своему значению и знаку и поэтому не могут
быть исключены из результатов измерений, как систематические погрешности.
Случайной называют такую величину, которая в результате опыта может
принимать то или иное значение, неизвестно заранее - какое именно.
Дискретные случайные величины – принимающие отделенные друг от
друга значения, которые можно заранее перечислить.
Непрерывные случайные величины - величины, возможные значения
которых непрерывно заполняют некоторый промежуток.

2.

m
x 1 , x 2 , x 3 , … xN
n1, n2, n3, … nm
∑ xi nk
N
x =∑ xi
k=1
x =
N
i=1
m
∑ nk
=N
k=1
Fk =
nk
N
m
При N →∞
Fk → pk
∑ pk
=1
k=1
pk – вероятность появления значения дискретной случайной величины

3.

Законом
случайной
распределения (законом
величины
распределения
называется
всякое
вероятности)
соотношение,
устанавливающее связь между возможными значениями случайной
величины и соответствующими им вероятностями.
X
X1
X2 X3
…
Xm
p
p1
p2
…
pm
p3
pk
x1 x2
xm
xk

4.

Числовые характеристики случайной величины:
Математическое ожидание
N
M(x) = x1 p1 + x2 p2 + …+ xN pN =∑ xi pi
i=1
оценкой математического ожидания является среднее арифметическое
Дисперсия - математическое ожидание квадрата отклонения случайной величины
от ее математического ожидания
N
D(x) = M [X – M(x)]2 =∑ [xi - M(x)]2 pi
i=1
Среднее квадратическое отклонение (СКО)
σx = √ D

5.

Непрерывная случайная величина имеет бесчисленное множество
возможных значений,
Для количественной характеристики распределения вероятности
непрерывной случайной величины пользуются не вероятностью события
X=x , а вероятностью события X x, где x – некоторая текущая
переменная
Функция распределения вероятности случайной величины X:
F(X) =P ( X x )
F(X) - интегральная функция распределения
или интегральный закон распределения

6.

Некоторые общие свойства функции распределения:
1. Функция распределения F(x) – неубывающая функция своего
аргумента,
т.е. при x2 x1
2. При x -
F(x2) F(x1)
F( - ) = 0,
т.е. на минус бесконечности функция распределения равна нулю.
3. При x + F(+ ) = 1,
т.е. на плюс бесконечности функция распределения равна единице.
Вероятность попадания случайной величины X в интервал [x1, x2]
P [ x1 X x2 ] = F(x2) - F(x1)

7.

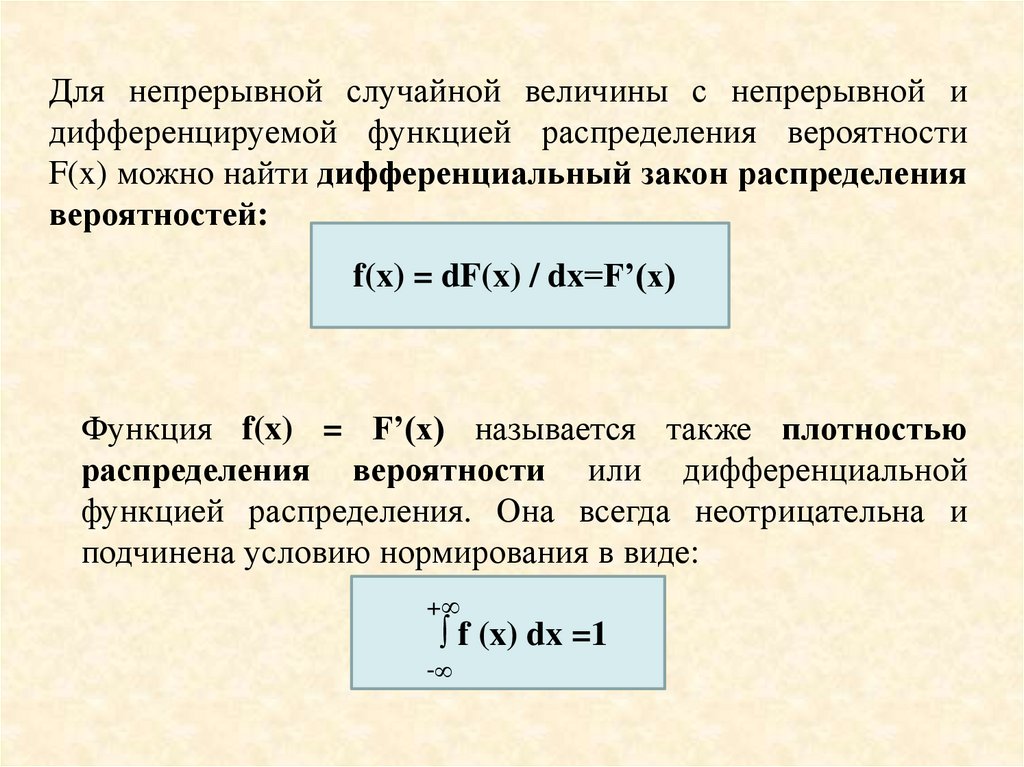
Для непрерывной случайной величины с непрерывной и
дифференцируемой функцией распределения вероятности
F(x) можно найти дифференциальный закон распределения
вероятностей:
f(x) = dF(x) / dx=F’(x)
Функция f(x) = F’(x) называется также плотностью
распределения вероятности или дифференциальной
функцией распределения. Она всегда неотрицательна и
подчинена условию нормирования в виде:
+
f (x) dx =1
-

8.

C
использованием
дифференциальной
функции
распределения
вероятность попадания случайной величины X в интервал [x1, x2]
равна :
x2
∫
P [ x1 X x2 ] = f(x) dx
x1
Перечень стандартных дифференциальных функций распределения
абсолютных погрешностей установлен ГОСТ 8.011-72.

9.

Равномерный
закон
возможные значения
распределения
случайной
случайной
величины
величины
находятся
в
-
пределах
некоторого конечного интервала, причем в пределах этого интервала все
значения случайной величины обладают одной и той же плотностью
вероятности.
1
f ( x)
x2 x1
f(x)
при x1 x x2
,
1/(x2 – x1)
x1
x2
x
f ( x) 0
,
при x x1
x x2

10.

Нормальное распределение случайной величины
(распределение Гаусса)
При нормальном законе распределения случайной величины функция
плотности вероятности имеет следующий вид:
2
( x mx )
1
f ( x)
exp
2
2 x
x 2
mx – математическое ожидание (среднее значение) случайной величины X,
x - среднее квадратическое отклонение (СКО) случайной величины X
относительно mx.

11.

Центральная предельная теорема теории вероятностей:
реальное распределение случайных погрешностей
(случайной величины) будет близко к нормальному
всякий раз, когда результаты наблюдений формируются
под влиянием большого числа независимо действующих
факторов, каждый из которых оказывает лишь
незначительное воздействие по сравнению с суммарным
воздействием всех остальных.

12.

f(x)
F(x)
1
1
x 2
-x
x
x

13.

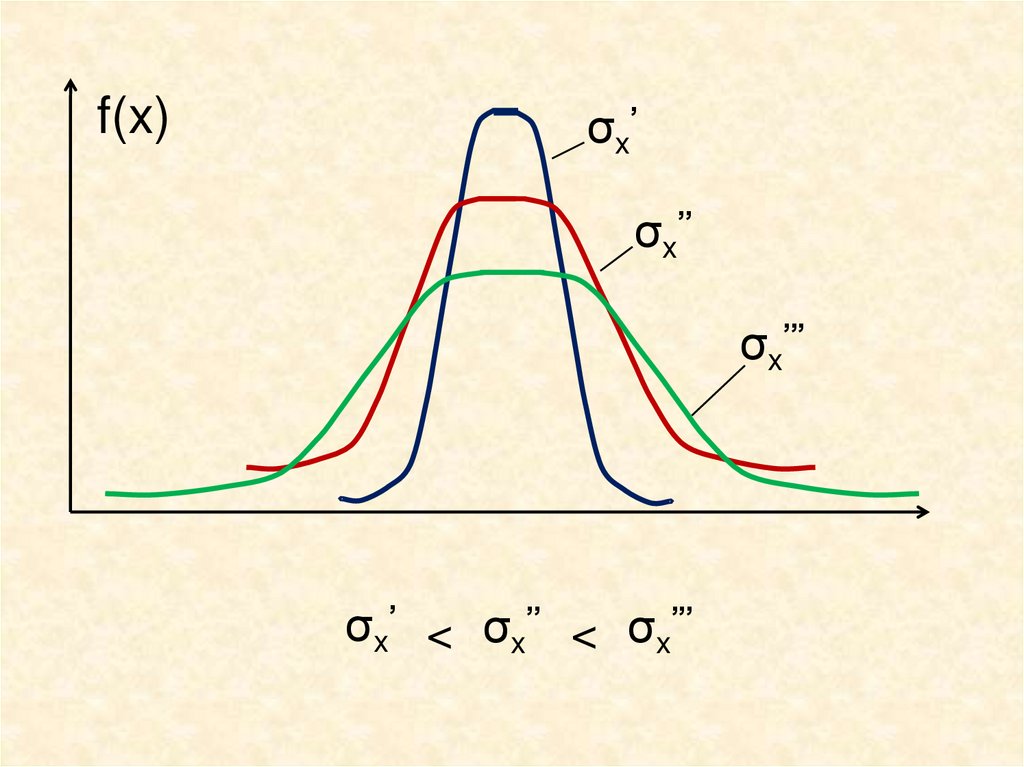
f(x)
σx’
σx’’
σx’’’
σx’ < σx’’ < σx’’’

14.

f ( x)
1
x
x mx
t
x
f ( x)
1
x
t2
exp
2
2
t2
1 2
exp dt F (t 2 ) F (t1 ) 2 F (t ) 1
2 t1
2
t
p [ x1 X x2 ]
( x mx ) 2
exp
2
2 x
2

15.

При n 30
Распределение Стьюдента
1
Г (n / 2)
t
f (t , n)
1
(n 1) Г [( n 1) / 2] n 1
2
где
n / 2
Г – гамма-функция
При n 30
распределение Стьюдента переходит в нормальное распределение
P [ x1 X x2 ] = 2 F (t, n) - 1
F (t, n) – интегральная функция Стьюдента,
значения которой табулированы

16.

Числовые характеристики закона распределения
начальные моменты
(усредняются значения, отсчитываемые от начала координат)
Моменты
центральные моменты
(усредняются значения, отсчитываемые от центра распределения)
Общее правило образования начальных моментов:
k
X
x
k
f ( x)dx
k – номер момента;
f(x) – функция распределения плотности вероятности

17.

Первый начальный момент - математическое ожидание
X
x f ( x)dx
≡ М(x) или
mx
Математическое ожидание служит для определения на числовой оси
среднего значения случайной величины, т.е. области вокруг которой
группируются значения случайной величины.

18.

Основные свойства математического ожидания:
1. М(а) =а; где а=const Математическое ожидание неслучайного
числа равно самому числу.
2. M(ax) = a M(x) Постоянный множитель можно выносить за знак
математического ожидания.
3. M(x+y-z) = M(x) + M(y) – M(z) Математическое ожидание суммы
независимых случайных величин равно алгебраической сумме их
математических ожиданий.
4. M(xyz) = M(x) M(y) M(z)
Математическое ожидание
произведения независимых случайных величин равно
алгебраической сумме их математических ожиданий.
5. M[x – M(x)] =0 Математическое ожидание отклонения случайной
величины от ее математического ожидания равно нулю.

19.

Если начало координат перенесено в центр закона
распределения вероятности, то такое распределение
называется центрированным.
Общее правило образования центральных моментов:
(X X )
k
( x x)
k
f ( x)dx

20.

( X X ) ( x x) f ( x)dx
k
k
1. Первый центральный момент равен нулю
2. Второй центральный момент – называется дисперсией
D(x) или σx2
x ( X X ) ( x x) f ( x)dx
2
2
2

21.

Основные свойства дисперсии:
1. D(a) =0, a=const
Дисперсия неcлучайного числа равна нулю.
2. D(ax) = a2 D(x)
Постоянный множитель можно выносить за
знак дисперсии, возводя его при этом в квадрат.
3. D(x + y - z) = D(x) + D(y) + D(z)
Дисперсия алгебраической
суммы независимых случайных величин равна арифметической
сумме их дисперсий.
4. D(x) = M(x2) – M2(x)
Дисперсия случайной величины равна
разности между математическим ожиданием ее квадрата и
квадратом математического ожидания.

22.

Чем больше дисперсия, тем значительнее рассеяние результатов
измерения относительно среднего значения.
В метрологии в качестве меры рассеяния используют
среднее квадратическое отклонение (СКО), которое по размерности
совпадает с измеряемой величиной.
x D(x)
или
x x
2
Третий центральный момент служит для оценки асимметрии плотности
распределения вероятности,
Четвертый центральный момент используется для оценки
заостренности функции плотности распределения вероятности

23.

Закон распределения суммы двух независимых случайных
величин, каждая из которых имеет свое распределение,
называется композицией
f(x1)
f(x2)
f(x1+x2) - композиция

24.

Примеры образования композиций законов распределения
f(x1)
x1
a
f(x2)
b
a-b
x2
f(x1 + x2)
x1 + x2
a+b

25.

Примеры образования композиций законов распределения
f(x1)
x1
a
f(x2)
a
x2
f(x1 + x2)
x1 + x2
2a

26.

Примеры образования композиций законов распределения
f(x1)
x1
a
f(x2)
a
x2
f(x1 + x2)
x1 + x2
2a

27.

Оценки, получаемые по данным измерений - случайные величины,
их значения зависят от числа измерений.
Оценки должны быть состоятельными, несмещенными и эффективными.
Оценка называется состоятельной, если при увеличении числа измерений она
стремится к истинному значению оцениваемой величины.
^
Q → Qист при n →
Оценка называется несмещенной, если ее математическое ожидание равно
истинному значению оцениваемой величины.
^
M(Qi) = Qист
Оценка называется эффективной, если из нескольких возможных несмещенных
оценок она имеет наименьшую дисперсию.
^
D(Qi) = min

28.

Для
независимых
прямых
равноточных
измерений,
подчиненных
центрированному симметричному закону распределения вероятности,
среднее арифметическое является состоятельной, несмещенной и
эффективной оценкой истинного значения измеряемой величины.
1 n
Q Qi
n i 1

29.

Для нормального закона распределения оценку СКО отдельных
результатов измерений в серии из n независимых равноточных измерений
вычисляют по формуле:
1 n
2
S
(
Qi
Q
)
(n 1) i 1
S- средняя квадратическая погрешность (СКП)
результатов единичных показаний в ряду измерений
σ^ x

30.

x
^
S
SQ
n
x
^
n
СКП среднего арифметического в n раз меньше, чем СКП результата
единичного измерения.
При этом если результаты единичного измерения подчиняются
нормальному закону распределения вероятности, то и среднее
арифметическое подчиняется нормальному закону с тем же
математическим ожиданием.
Для равномерного закона распределения
x1 x2
x
2
x
x 2 x1
2 3