Сравнение нескольких групп: дисперсионный анализ. Лекция 5

1. ЛЕКЦИЯ 5

2
A
2
e
s
F
s
СРАВНЕНИЕ НЕСКОЛЬКИХ
ГРУПП: ДИСПЕРСИОННЫЙ
АНАЛИЗ

2. 5.1. Параметрические и непараметрические критерии

3.

Биология сегодня – экспериментальная
наука, а решение экспериментальных задач
не обходится без сравнений.
Сравнение позволяет установить,
насколько наблюдаемые различия
существенны (т.е. доказать, что
определенный фактор оказывает влияние на
изучаемый признак).

4.

Статистический тест – процедура расчета
критерия значимости.
Критерий значимости – количественная
характеристика, позволяющая оценить
статистическую значимость различий
между выборками.

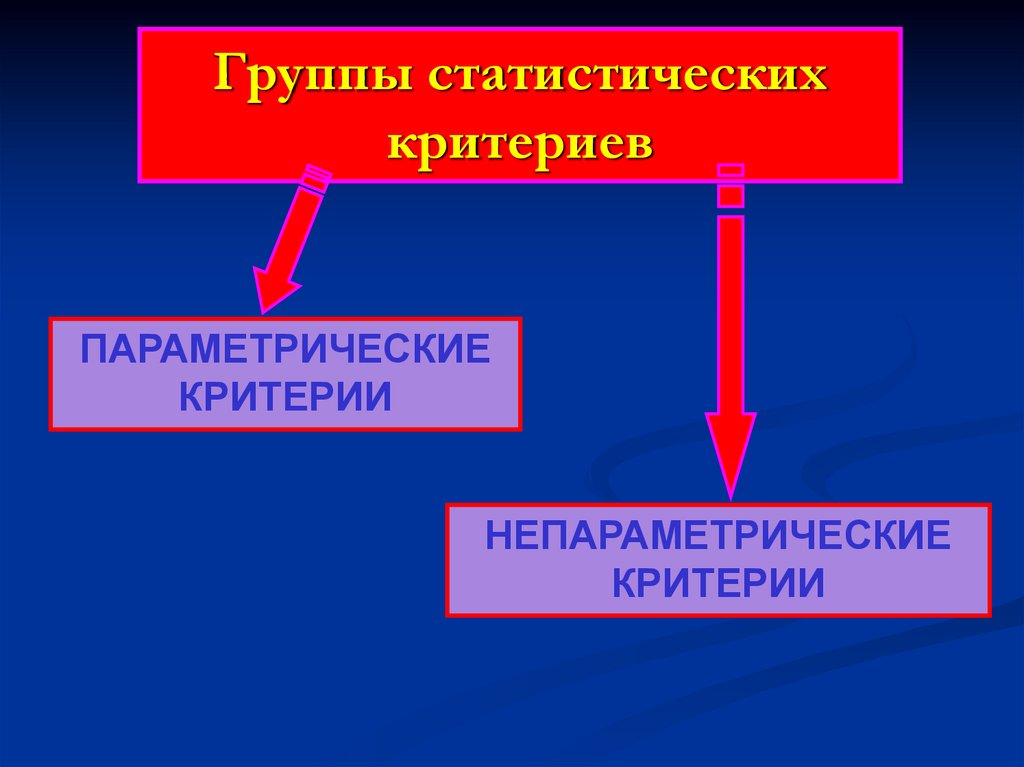
5. Группы статистических критериев

ПАРАМЕТРИЧЕСКИЕ
КРИТЕРИИ
НЕПАРАМЕТРИЧЕСКИЕ
КРИТЕРИИ

6.

ПАРАМЕТРИЧЕСКИЕ
КРИТЕРИИ
расчет основан на
параметрах,
характеризующих
распределение
выборочных единиц,
требуют нормального
распределения данных,
n>20
НЕПАРАМЕТРИЧЕСКИЕ
КРИТЕРИИ
не требуют, чтобы
данные подчинялись
нормальному закону
распределения

7. Почему параметрическим критериям следует отдавать предпочтение???

В сравнении с
непараметрическими,
параметрические критерии
обладают большей мощностью,
т.е. способностью выявлять
различия между выборками.

8. 5.2. Дисперсионный анализ: постановка задачи

9. Дисперсионный анализ (ANOVA, от англ. analysis of variance)

Предназначен для одновременного
сравнения арифметических средних
нескольких выборок (2 и более).
Разработан Рональдом Фишером в
20-х гг. прошлого столетия.

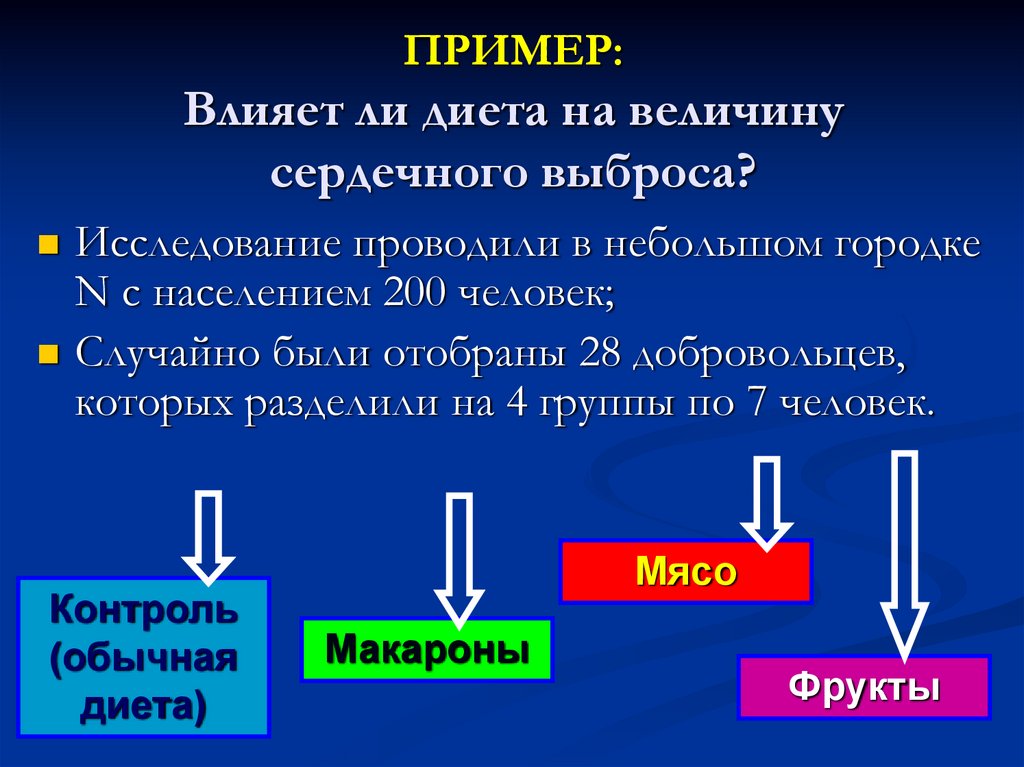
10. ПРИМЕР: Влияет ли диета на величину сердечного выброса?

Исследование проводили в небольшом городке
N с населением 200 человек;
Случайно были отобраны 28 добровольцев,
которых разделили на 4 группы по 7 человек.
Контроль
(обычная
диета)
Мясо
Макароны
Фрукты

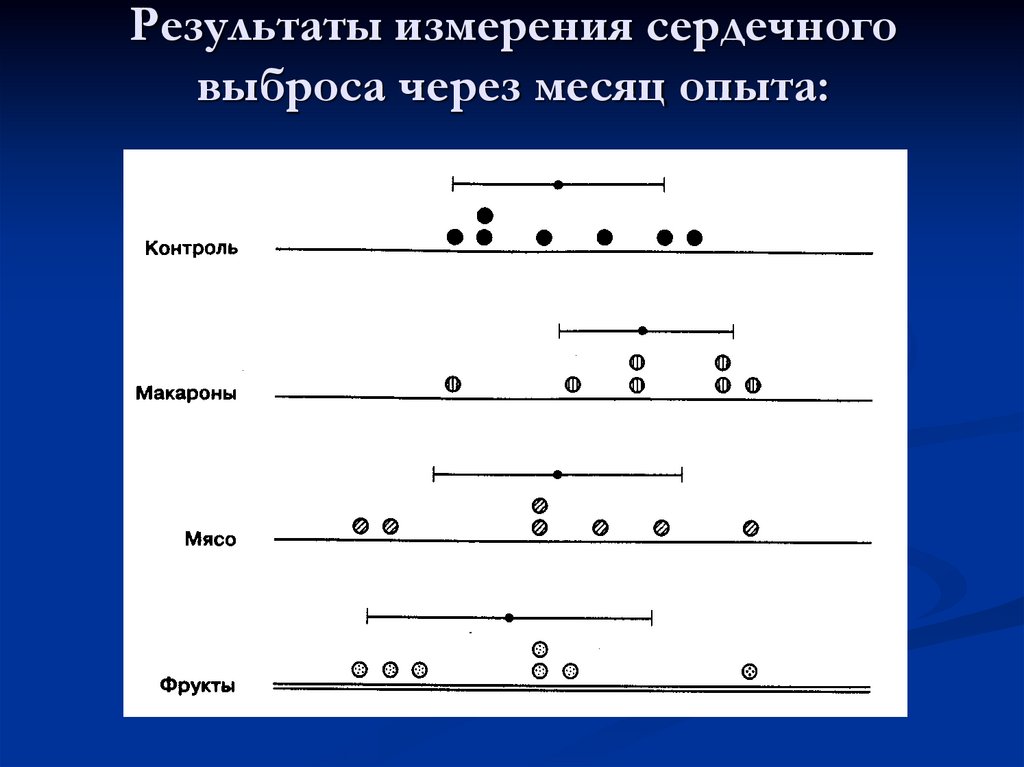
11. Результаты измерения сердечного выброса через месяц опыта:

12. С чего начать анализ?

Перед выполнением любого статистического
теста формулируется т.н. нулевая гипотеза
(Н0)
В нашем случае Н0: диета не оказывает
никакого влияния на величину сердечного
выброса,
т.е. наблюдаемая разница между средними
значениями выброса в экспериментальных
группах несущественна и вызвана случайными
факторами.

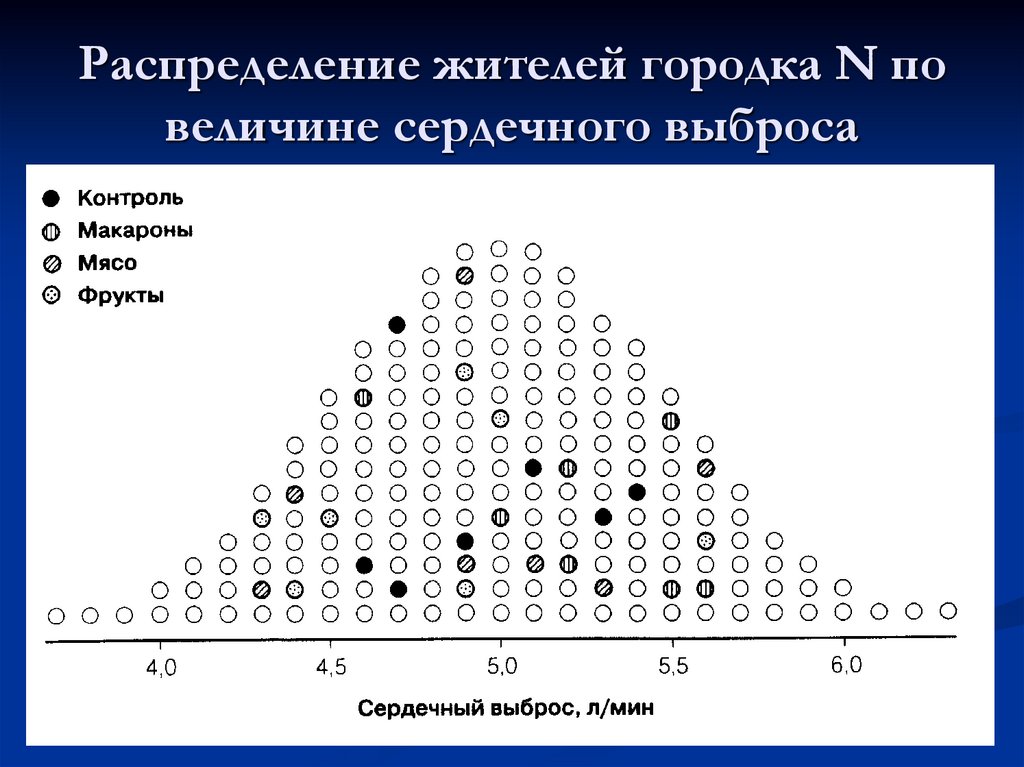
13. Распределение жителей городка N по величине сердечного выброса

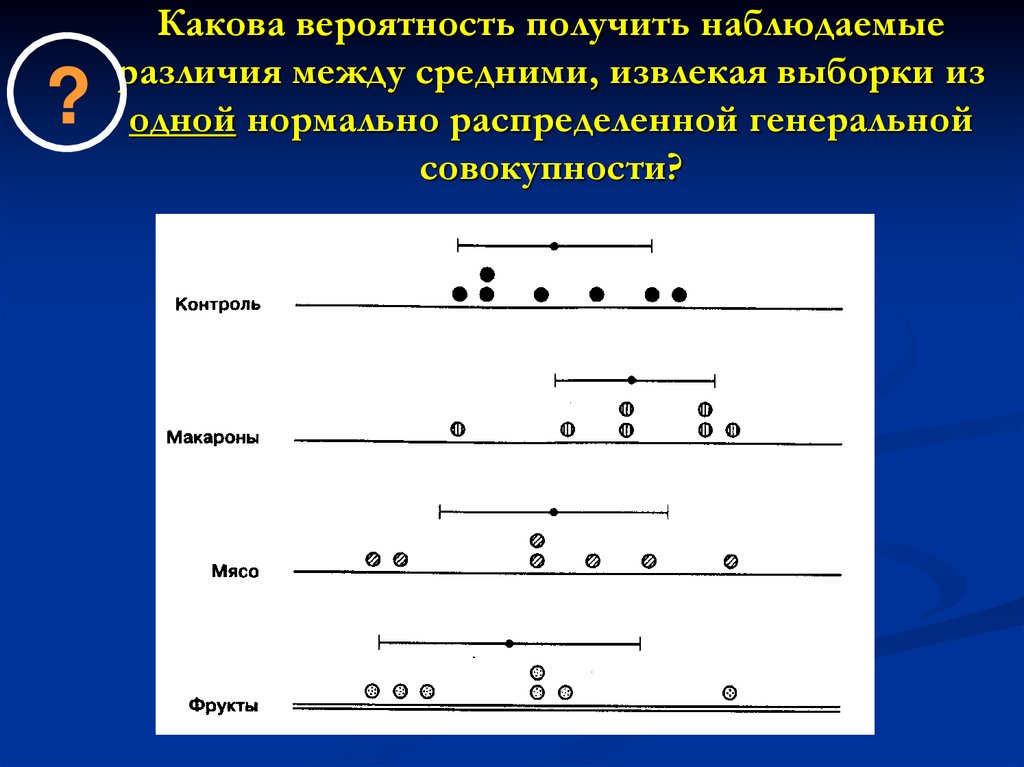
14. Какова вероятность получить наблюдаемые различия между средними, извлекая выборки из одной нормально распределенной генеральной

?
Какова вероятность получить наблюдаемые
различия между средними, извлекая выборки из
одной нормально распределенной генеральной
совокупности?

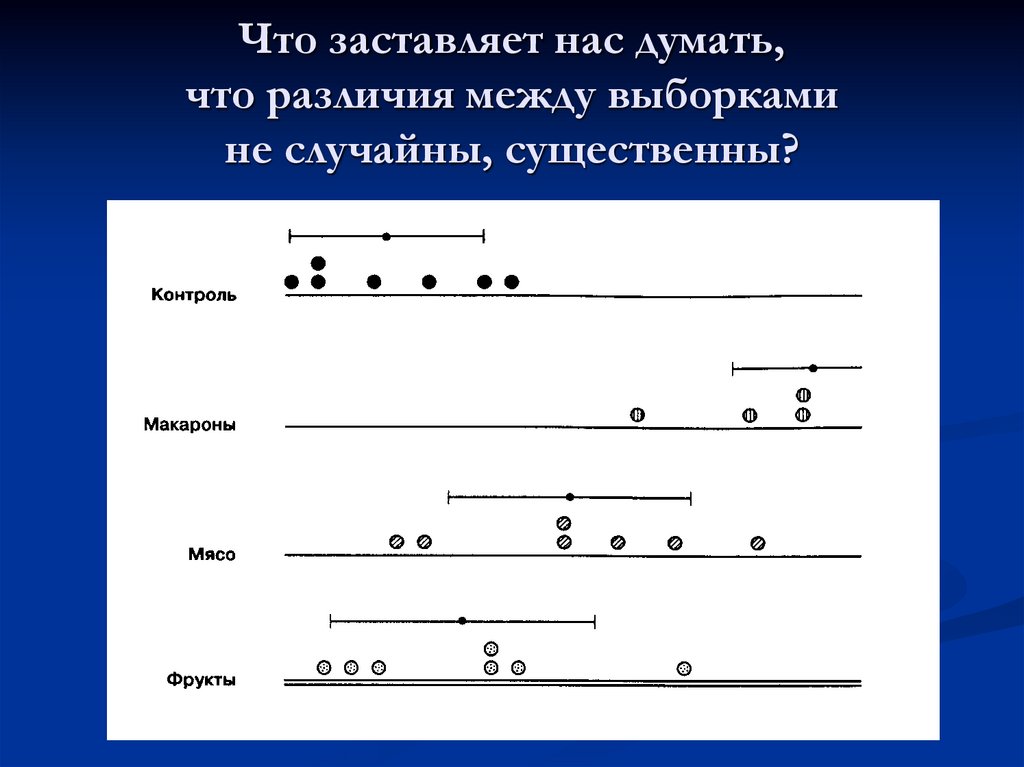
15. Что заставляет нас думать, что различия между выборками не случайны, существенны?

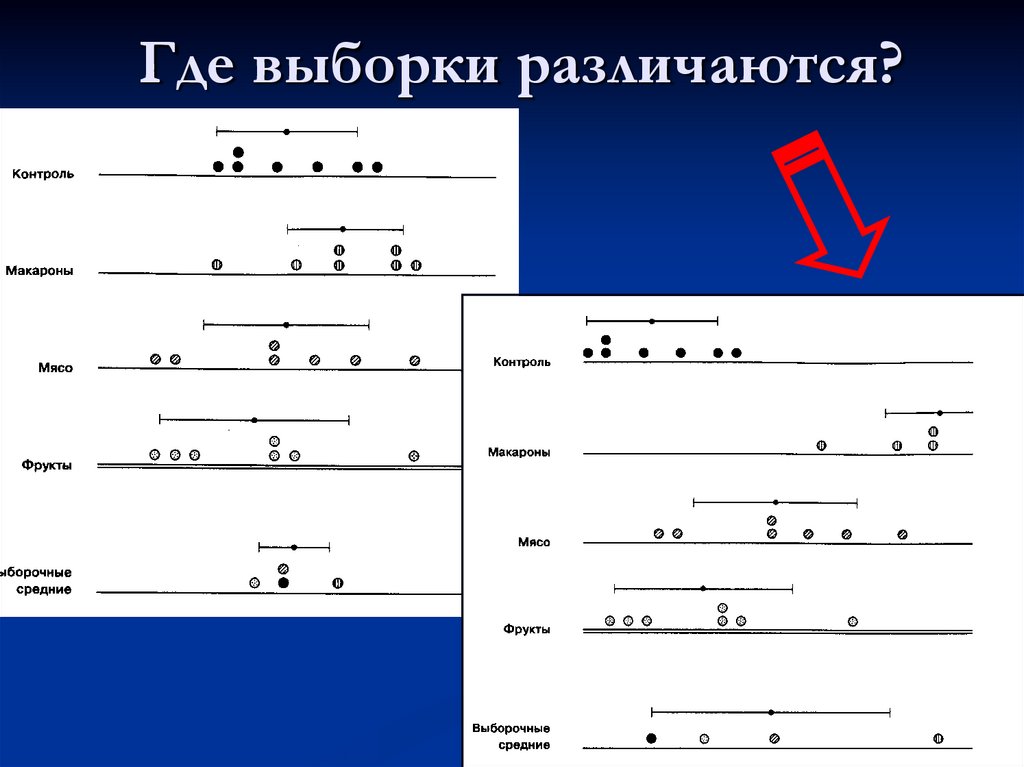
16. Где выборки различаются?

17. Еще один пример различающихся выборок

18. Разброс значений выборочных средних и разброс значений внутри групп можно оценить при помощи дисперсии

Дисперсия правильно
характеризует разброс в случае
нормального распределения =>
параметрический метод

19. 5.3. Две оценки дисперсии в ANOVA

20. Дисперсию генеральной совокупности можно оценить двумя способами:

На основе выборочных дисперсий;
По разбросу выборочных средних.
(!) Если выборки принадлежат одной
генеральной совокупности, оба способа
оценки дисперсии дадут примерно
одинаковые результаты => Н0

21. Если два способа оценки дисперсии генеральной совокупности дают разные результаты, то принимаем альтернативную гипотезу НА:

Маловероятно, что мы получили бы
наблюдаемые различия между групповыми
средними, если бы они были просто
случайными выборками из одной
нормально распределенной генеральной
совокупности.

22. Находим внутригрупповую (=остаточную, шумовую) дисперсию:

1
Находим внутригрупповую
(=остаточную, шумовую)
дисперсию:
s2вну = ¼(s2кон + s2мак + s2мяс + s2фру)

23. Оцениваем дисперсию генеральной совокупности по разбросу выборочных средних – межгрупповую (факториальную) дисперсию:

2
Оцениваем дисперсию генеральной
совокупности по разбросу выборочных
средних – межгрупповую (факториальную)
дисперсию:
Так как σx = σ / √n, то: σ2 = nσ2x
Используя выборочные средние, получаем:
s2меж = ns2x ,
где s2x – квадрат стандартного отклонения
выборки из выборочных средних.

24. Сравниваем межгрупповую и внутригрупповую оценки дисперсии

3
Сравниваем межгрупповую и
внутригрупповую оценки дисперсии
2
F=s
меж
2
/s
вну

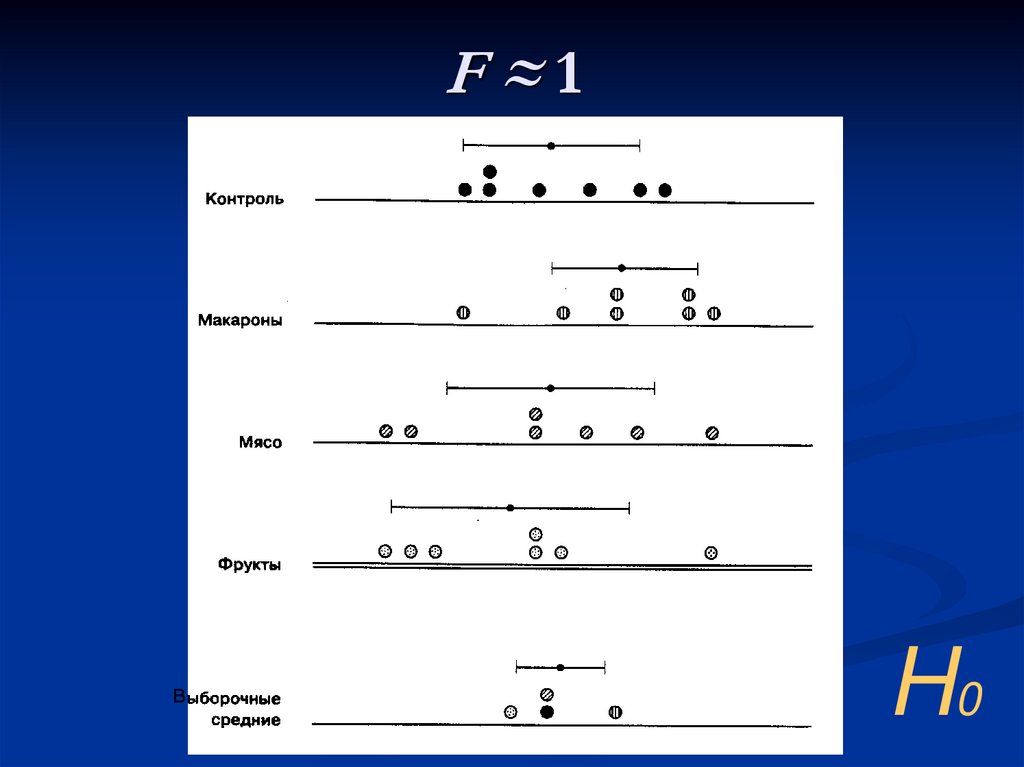
25. F ≈ 1

F≈1
в
H0

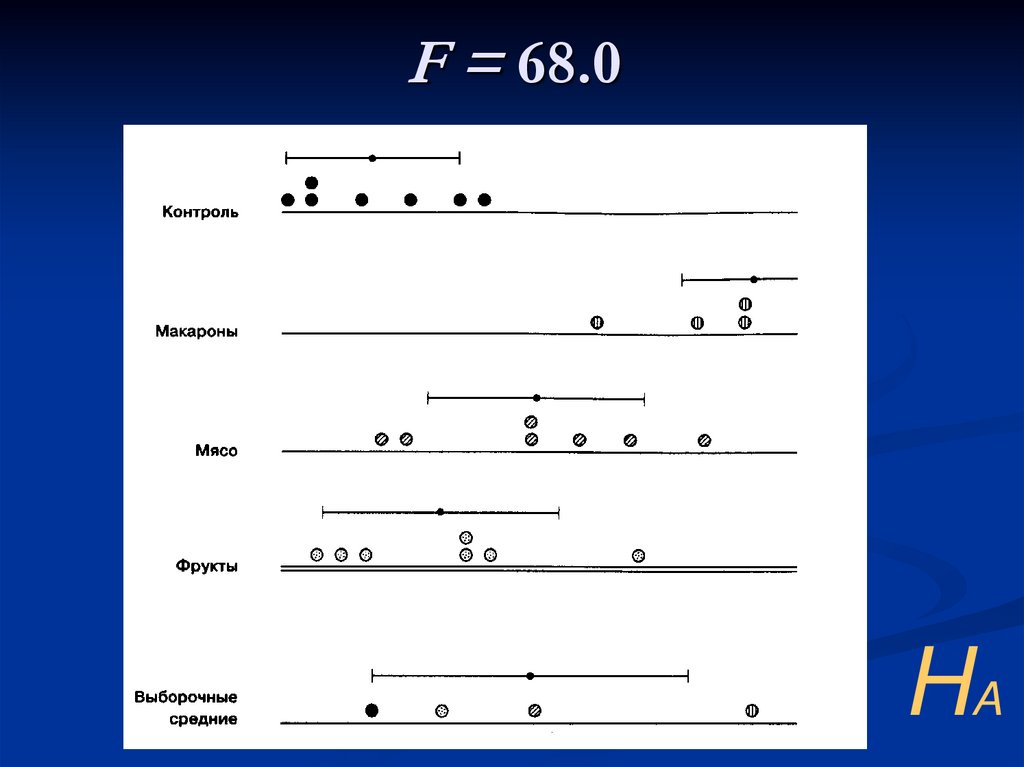
26. F = 68.0

HA

27. 5.4. Критическое значение F-критерия

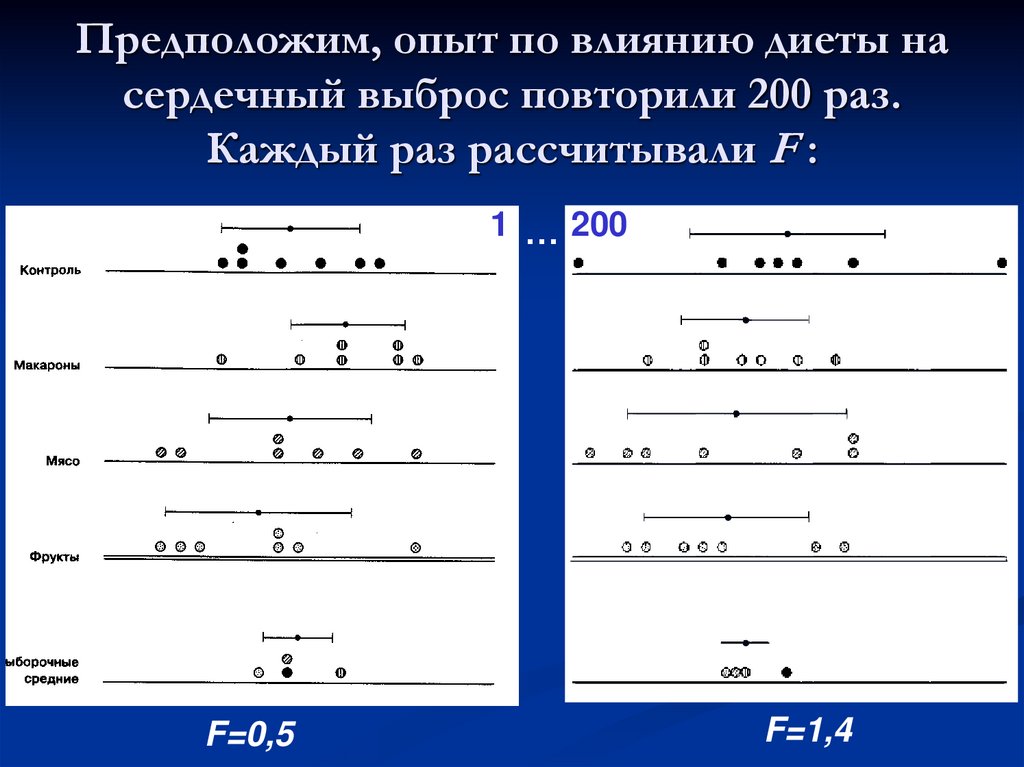
28. Предположим, опыт по влиянию диеты на сердечный выброс повторили 200 раз. Каждый раз рассчитывали F :

.
1 … 200
.
.
.
.
F=0,5
F=1,4

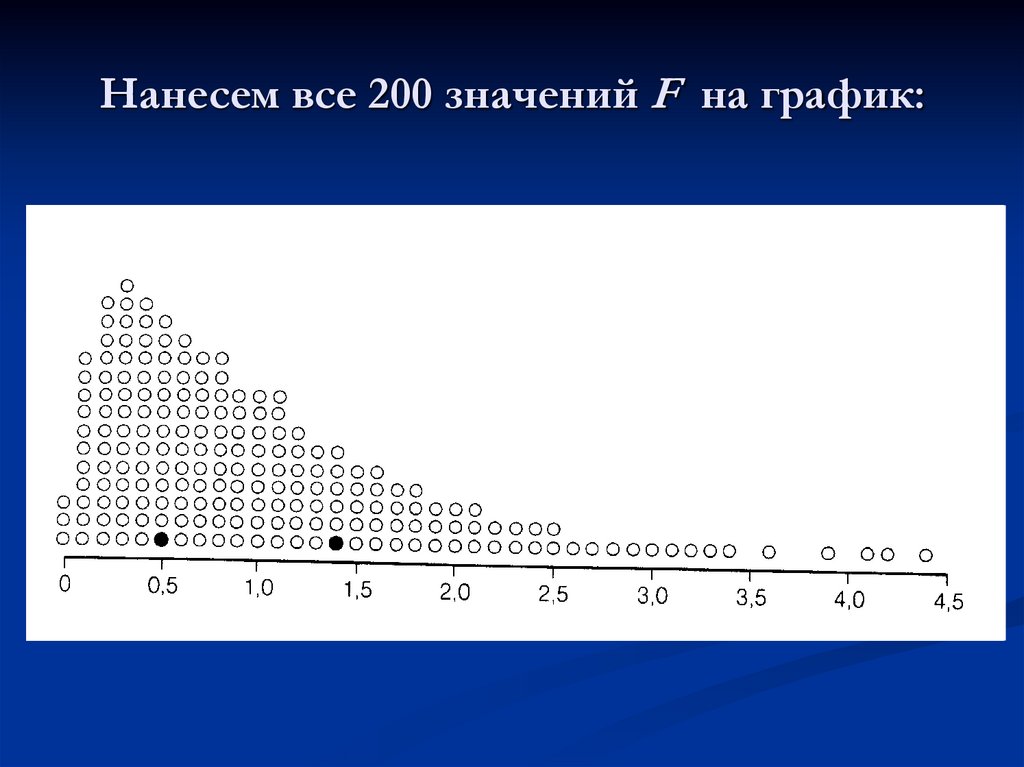
29. Нанесем все 200 значений F на график:

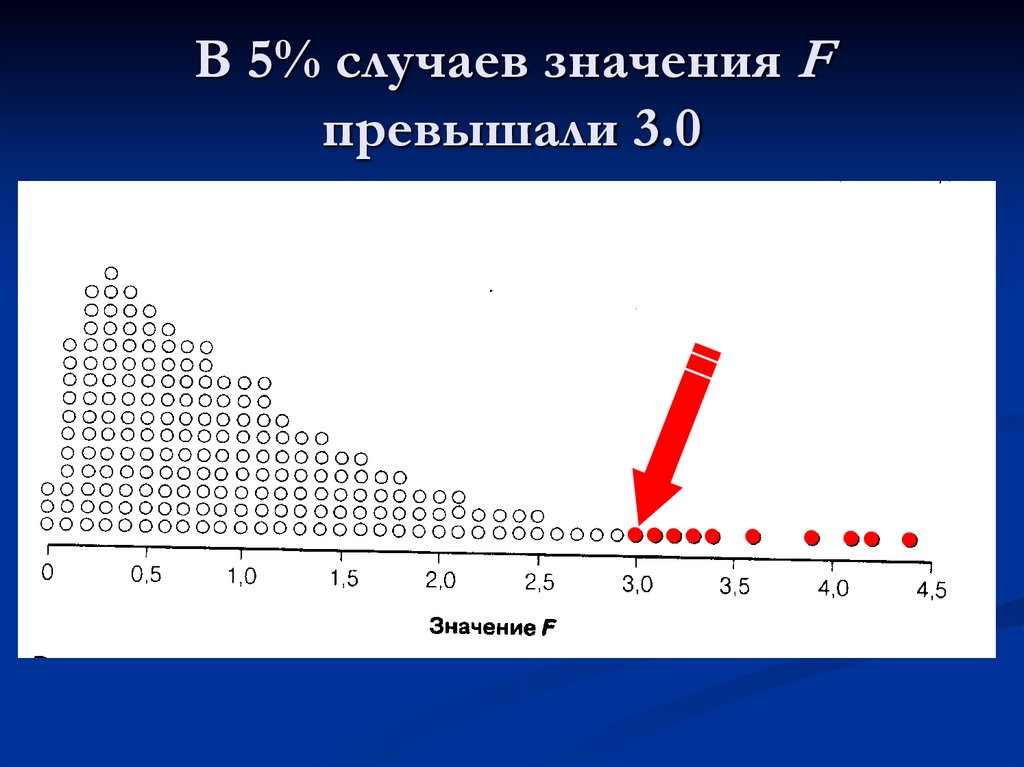
30. В 5% случаев значения F превышали 3.0

31.

Значение любого статистического
критерия, начиная с которого мы
отвергаем нулевую гипотезу,
называется критическим
значением.

32.

Р – вероятность
справедливости нулевой
гипотезы.
рассчитывают в ходе выполнения теста

33.

Максимальная приемлемая вероятность
ошибочно отвергнуть верную нулевую
гипотезу называется уровнем
значимости (α).
Уровни значимости,
используемые в биологии:
α = 0.05 (5%) – чаще всего
α = 0.01 (1%)
α = 0.001 (0.1%)

34. Интерпретация Р:

Если Р > α, то сохраняем H0
Если Р < α, то принимаем HA
ЗАПОМНИТЬ
НА ВСЮ ЖИЗНЬ!!!

35. Статистические ошибки:

I рода: отрицание нулевой
гипотезы, когда она фактически
истинна;
II рода: принятие нулевой
гипотезы, когда она на самом
деле не верна.

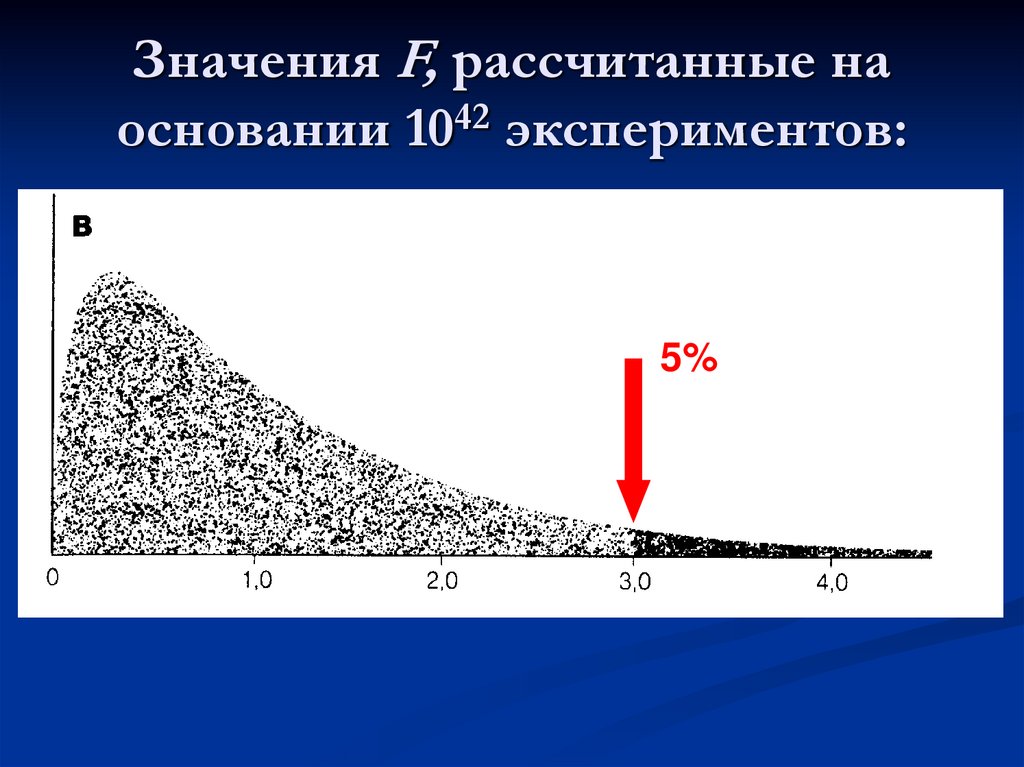
36. Значения F, рассчитанные на основании 1042 экспериментов:

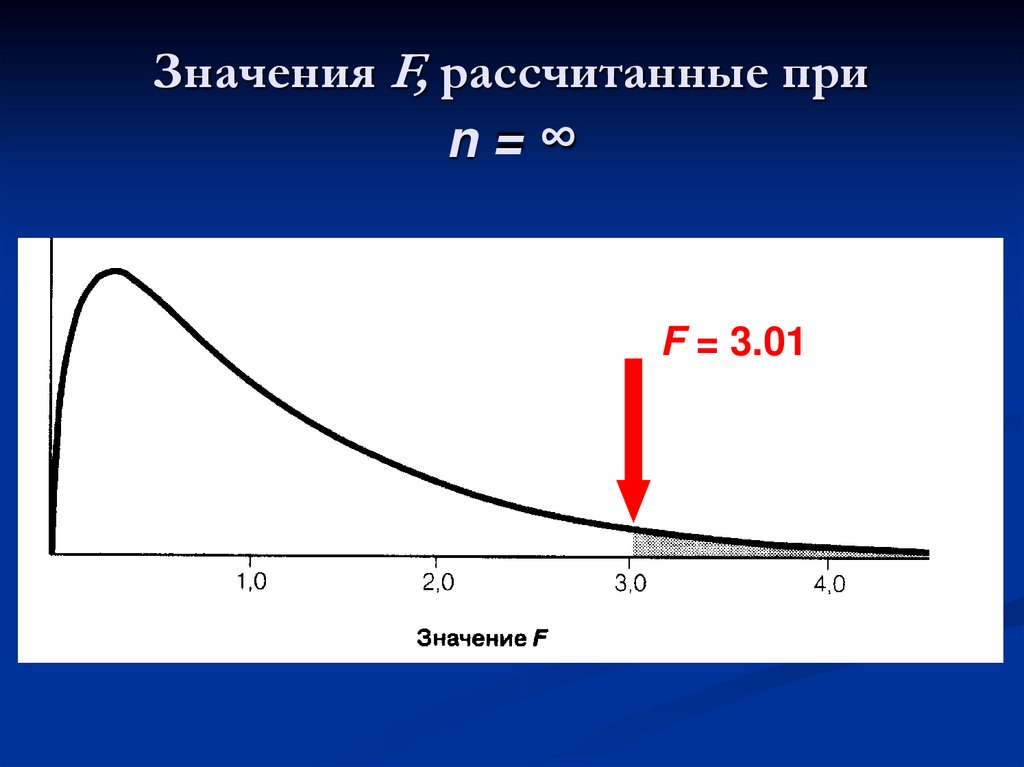
5%

37. Значения F, рассчитанные при n = ∞

Значения F, рассчитанные при
n=∞
F = 3.01

38. Чем определяется критическое значение F ?

Критическим уровнем
значимости (α) ;
Внутригрупповым и
межгрупповым числом степеней
свободы

39. Как рассчитать внутри- и межгрупповое число степеней свободы ?

υмеж = т – 1
υвну = m(n – 1)
В примере с диетами:
υмеж = 4 – 1 = 3
υвну = 4(7 – 1) = 24

40. Условия применения рассмотренного варианта дисперсионного анализа:

Каждая выборка независима от других;
Каждая выборка случайным образом
извлечена из исследуемой совокупности;
Совокупность нормально распределена;
Дисперсии сравниваемых выборок
однородны (статистически
не различаются).

41. 5.5. Трансформация данных

42. Логарифмическое преобразование данных

помогает в тех случаях, когда значения средних
арифметических положительно связаны с
величинами дисперсии
x log x
x log( x 1)

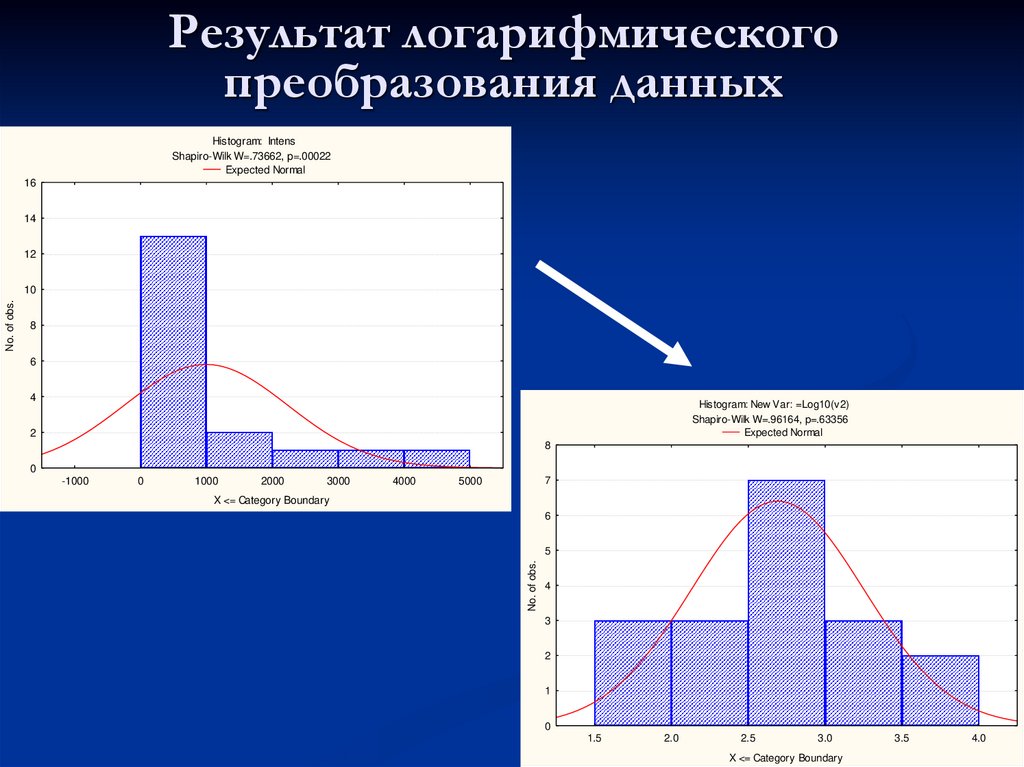
43. Результат логарифмического преобразования данных

Histogram: Intens
Shapiro-Wilk W=.73662, p=.00022
Expected Normal
16
14
12
8
6
4
Histogram: New Var: =Log10(v2)
Shapiro-Wilk W=.96164, p=.63356
Expected Normal
2
8
0
-1000
0
1000
2000
3000
4000
7
5000
X <= Category Boundary
6
5
No. of obs.
No. of obs.
10
4
3
2
1
0
1.5
2.0
2.5
3.0
X <= Category Boundary
3.5
4.0

44. Преобразование данных, распределенных по закону Пуассона или биномиальному закону

x x
x x 0.5

45. Преобразование данных, распределенных по закону Пуассона или биномиальному закону

3
x x
8
x x x 1

46. Преобразование Бокса-Кокса (Box-Cox transformation)

x
( x 1)

47. Угловое преобразование

применяется в случае с процентными
данными и долями
x arcsin x