Похожие презентации:
Элементы теории множеств. Лекция 2
1.
Основы системного анализа иматематической обработки информации
Представление
информации
средствами
множеств и математической логики
Лекция 2.
Элементы теории множеств
теории
2.
Начиная с XX века, появляетсятенденция к общей математизации наук.
Одним из проявлений этой тенденции
является
обращение
к
теории
множеств.
Больцано, Кантор, Веерштрасс
основоположники теории множеств
–
3.
Множество – совокупность объектов какой-либоприроды, воспринимаемых как единое целое.
Рассуждения об абстрактных множествах не
зависят от природы элементов.
В современной математике понятие множества
считается одним из основных. Универсальность
этого понятия в том, что под него можно подвести
любую совокупность предметов. Здесь годится все
— марки, числа, люди, точки, звезды, векторы,
тигры, функции и т.д.
Даже сами множества могут объединяться во
множества. Например, математики говорят про
множество фигур на плоскости, про множество тел
в пространстве, но каждую фигуру, каждое тело они
мыслят как множество точек.
4.
Можно привести следующие примеры множеств:1)учебники по математике;
2)студенты в группе;
3)преподаватели в аудитории;
4)точки плоскости.
Предметы, из которых состоит множество,
называются его элементами (например, буква К—
элемент множества букв русского алфавита).
Множество {дни недели} состоит и зэлементов:
понедельник, вторник, среда, четверг, пятница,
суббота, воскресенье.
Обозначения: А, В, С, …
a А – элемент a принадлежит множеству А.
b B – элемент b не принадлежит множеству B.
5.
Множество, количество элементов которого выражается некоторымчислом, называется конечным.
Примеры конечных множеств:
1)студенты-отличники в университете;
2)песчинки в мешке с песком.
Множество, содержащее бесконечное число элементов, называется
бесконечным.
Например, множество звезд во Вселенной.
Множество, которое не содержит ни одного элемента, называется
пустым и обозначается символом ∅.
Можно привести следующие примеры пустых множеств:
1)люди, имеющих рост 5см;
2)натуральные числа, расположенные в натуральном ряду между
числами 6 и 7.
В пустом множестве количество элементов выражается числом 0,
следовательно, оно конечное.
Иногда бывает трудно сказать, пусты ли те или иные множества.
Например, до сих пор неизвестно, пусто ли множество всех живых
динозавров на земном шаре. Если чудовище озера Лох-Несс
действительно окажется динозавром, то это множество не пусто.
6.
Способы задания множествПеречисление всех элементов множества
А= {1, 3, а, с};
В={река Волга, город Москва, планета
Меркурий};
Задание множества характеристическим
свойством элементов
A={a / прилагательные русского языка}
В такой записи правило, задающее
множество, отделено вертикальной чертой
Задание множества с помощью диаграммы
(круги Эйлера
или диаграммы Вена)
7.
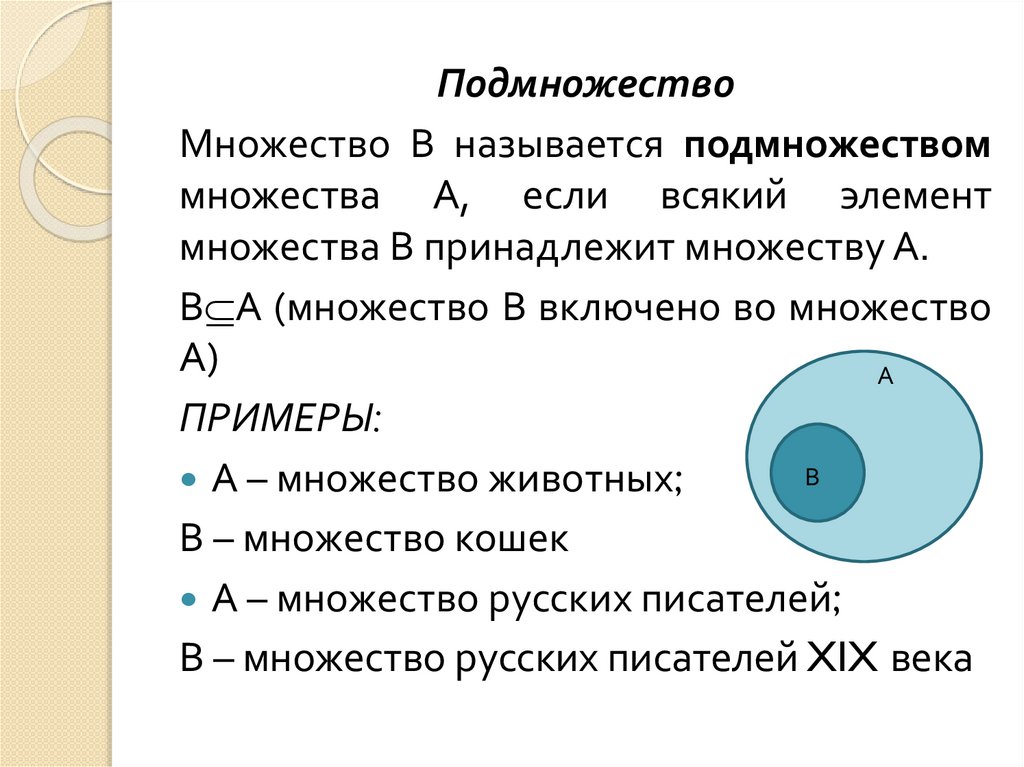
ПодмножествоМножество В называется подмножеством
множества А, если всякий элемент
множества В принадлежит множеству А.
В А (множество В включено во множество
А)
А
ПРИМЕРЫ:
В
А – множество животных;
В – множество кошек
А – множество русских писателей;
В – множество русских писателей XIX века
8.
Пустоемножество
является
подмножеством
любого
другого
множества
ПРИМЕР: Найти все подмножества
множества А={a, b, c}
РЕШЕНИЕ:
А1= , А2={a}, А3={b}, А4={c}, А5={a, b},
А6={a,c}, А7={b, c}, А8={a, b, c}
9.
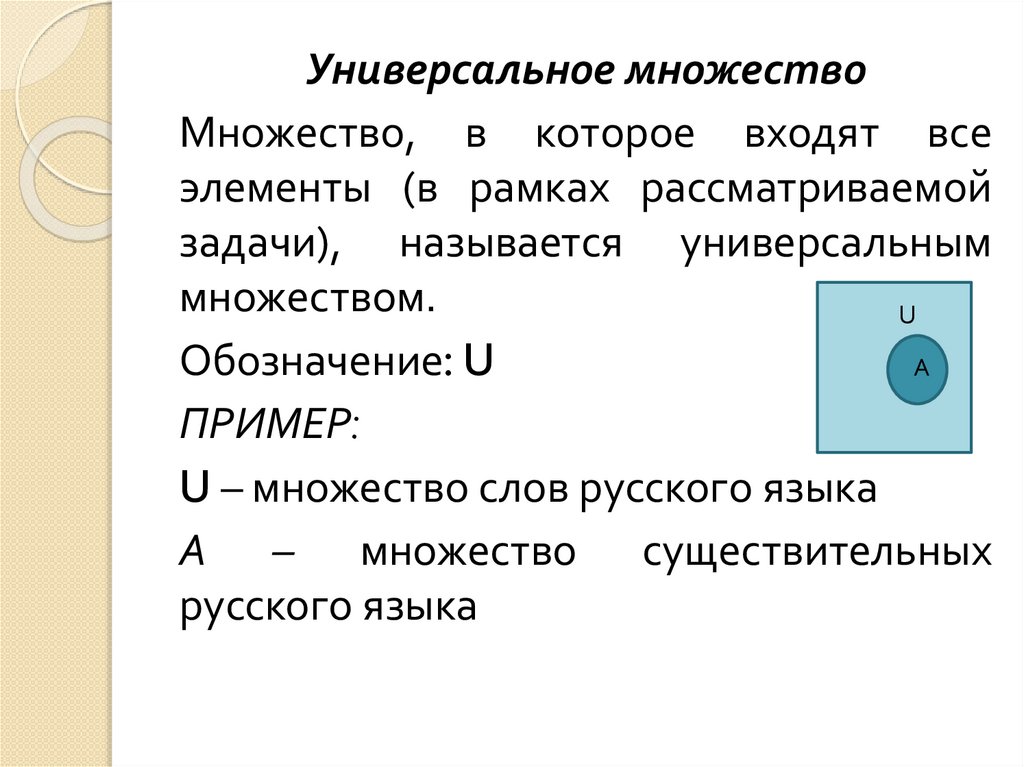
Универсальное множествоМножество, в которое входят все
элементы (в рамках рассматриваемой
задачи), называется универсальным
множеством.
U
Обозначение: U
А
ПРИМЕР:
U – множество слов русского языка
А – множество существительных
русского языка
10.
Отношения между множествамиМножества А и В не имеют общих
элементов
B
A
a А a B и b B b A
Пример: А – множество гласных букв
русского алфавита;
В – множество согласных букв русского
алфавита.
11.
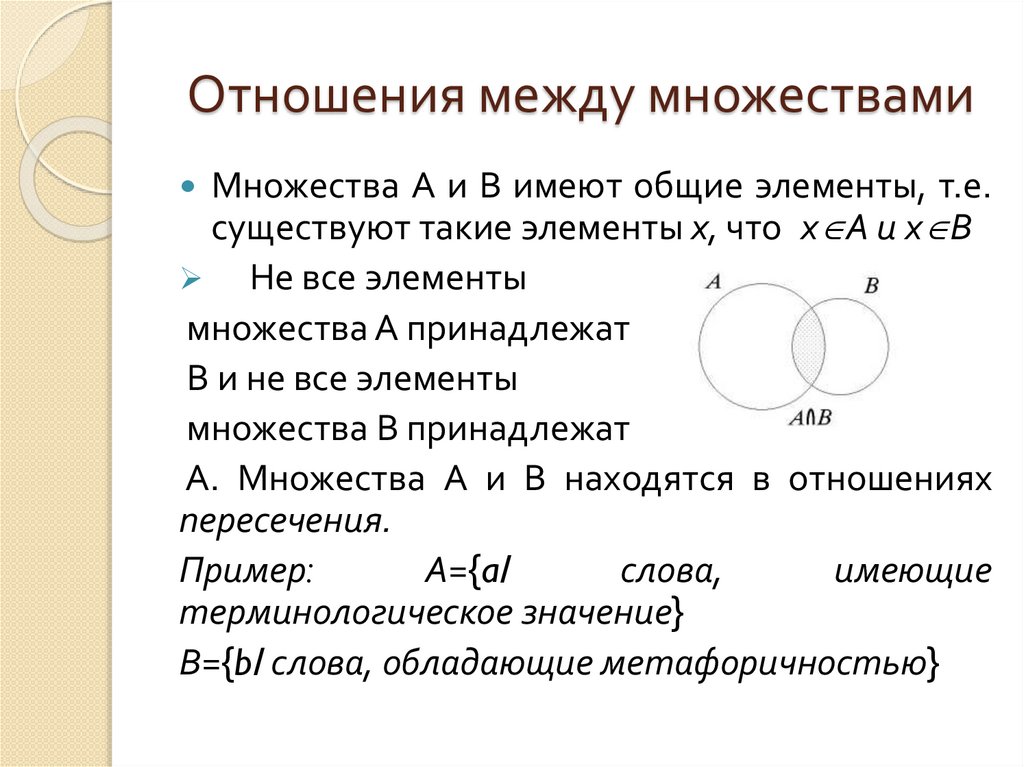
Отношения между множествамиМножества А и В имеют общие элементы, т.е.
существуют такие элементы х, что х А и х В
Не все элементы
множества А принадлежат
В и не все элементы
множества В принадлежат
А. Множества А и В находятся в отношениях
пересечения.
Пример:
А={a/
слова,
имеющие
терминологическое значение}
В={b/ слова, обладающие метафоричностью}
12.
Отношения между множествамиВсе элементы
множества В принадлежат А ,
множество А может содержать элементы, не
принадлежащие множеству В. Множества А и
В находятся в отношениях включения.
В А (множество В включено во множество А)
Все элементы множества А принадлежат В и все
элементы множества В принадлежат А.
Множества А и В находятся в отношениях
равенства.
Свойства отношения равенства множеств
1. А=А (рефлексивность)
2. А=В В=А (симметричность)
3. А=В и В=С А=С (транзитивность)
13.
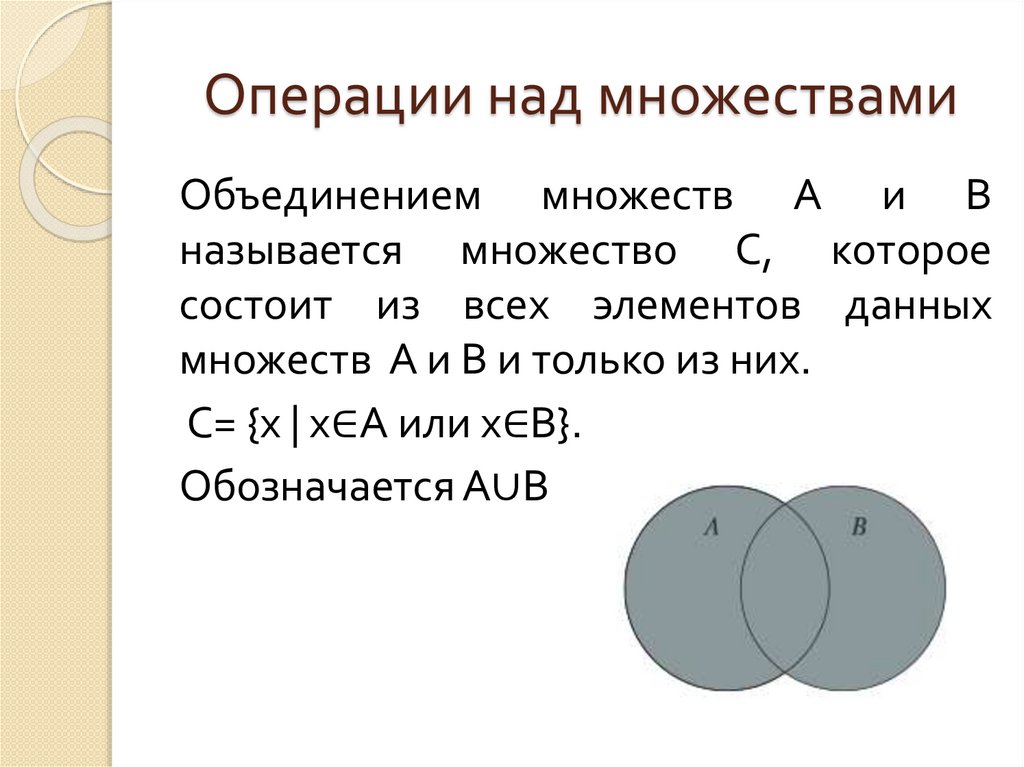
Операции над множествамиОбъединением множеств А и В
называется множество С, которое
состоит из всех элементов данных
множеств А и В и только из них.
С= {х | х∈А или х∈В}.
Обозначается А∪В
14.
Практически объединение множеств можно найти так:взять все элементы первого множества и приписать к
ним элементы из второго множества, которых нет в
первом.
ПРИМЕР: А={a, b, c, d, I, k, m, p}
B={b, c, I, n, o, p}
A B={a, b, c, d, I, k, m, p, n, o}.
Если А — множество студентов, не сдавших первый
экзамен, В — второй, тоА∪В — множество студентовзадолжников после двух экзаменов (не исключено, что ктотонесдал оба экзамена).
Свойства операции объединения множеств:
1.
А В=В А (коммутативность)
2.
А (В С)=(А В) С (ассоциативность)
3.
А А=А (иденпотентность)
4.
А =А
5.
А U=U
6.
Если А В, то А В=В.
15.
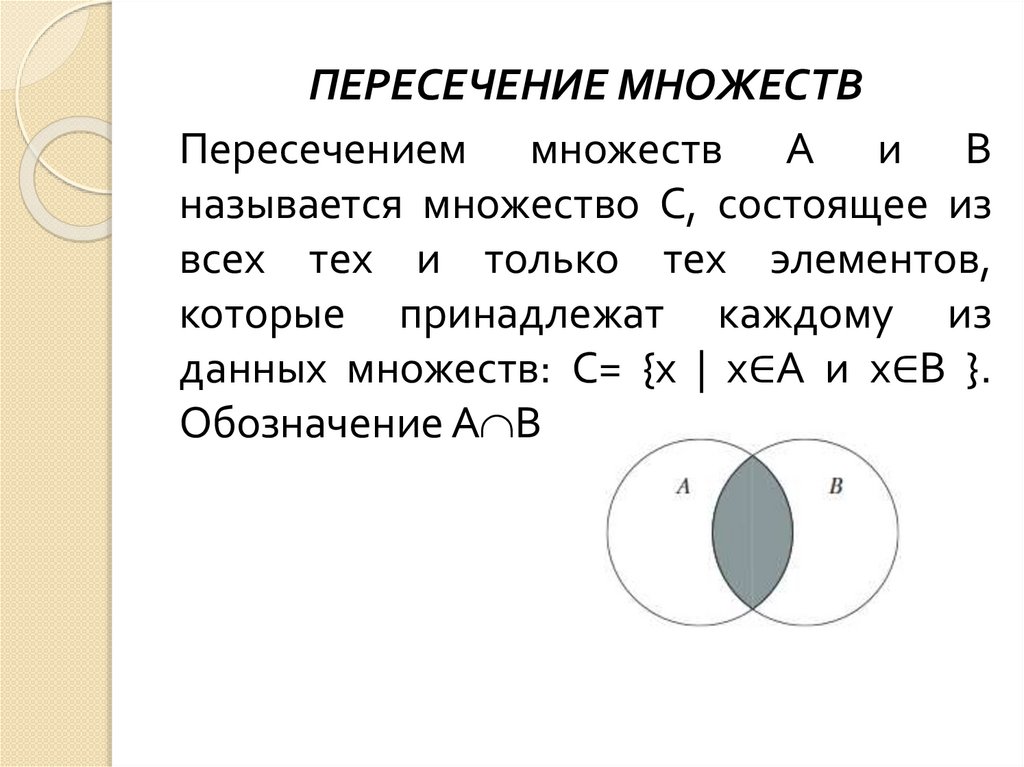
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВПересечением множеств А и В
называется множество С, состоящее из
всех тех и только тех элементов,
которые принадлежат каждому из
данных множеств: С= {х | х∈А и х∈В }.
Обозначение А В
16.
Пусть A= {1; 2; 3}, B= {2; 3; 4; 5}, D= {10; 11},тогда A∩B= {2; 3}, A∩D= ∅
Свойства операции пересечения
множеств
1. А В=В А (коммутативность)
2. А (В С)=(А В) С (ассоциативность)
3. А А=А (иденпотентность)
4. А =
5. А U=А
6. А (В С)=(А В) (А С)
7. А (В С)=(А В) (А С)
17.
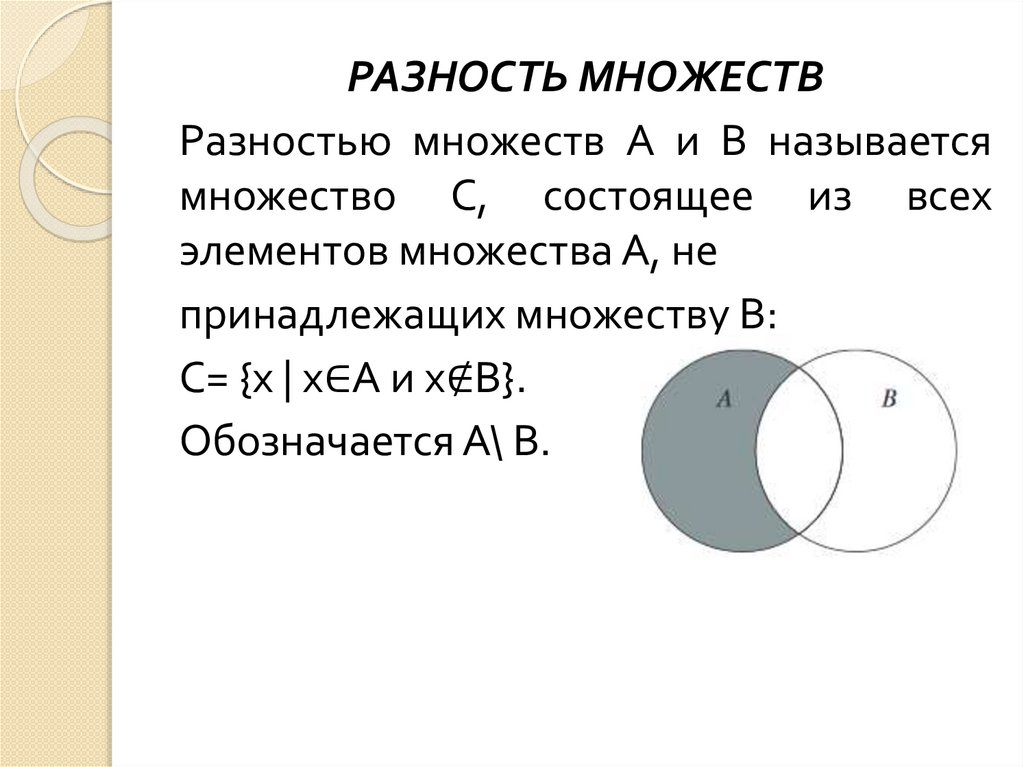
РАЗНОСТЬ МНОЖЕСТВРазностью множеств А и В называется
множество С, состоящее из всех
элементов множества А, не
принадлежащих множеству В:
С= {х | х∈А и х∉В}.
Обозначается А\ В.
18.
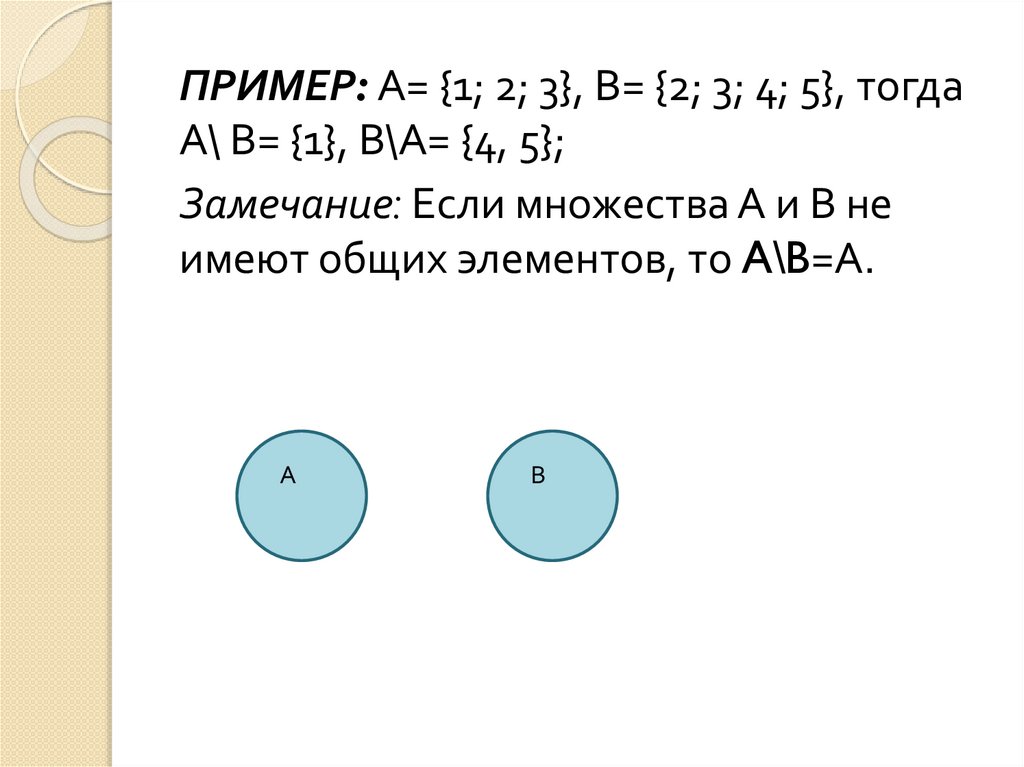
ПРИМЕР: A= {1; 2; 3}, B= {2; 3; 4; 5}, тогдаА\ В= {1}, В\А= {4, 5};
Замечание: Если множества А и В не
имеют общих элементов, то A\B=А.
А
В
19.
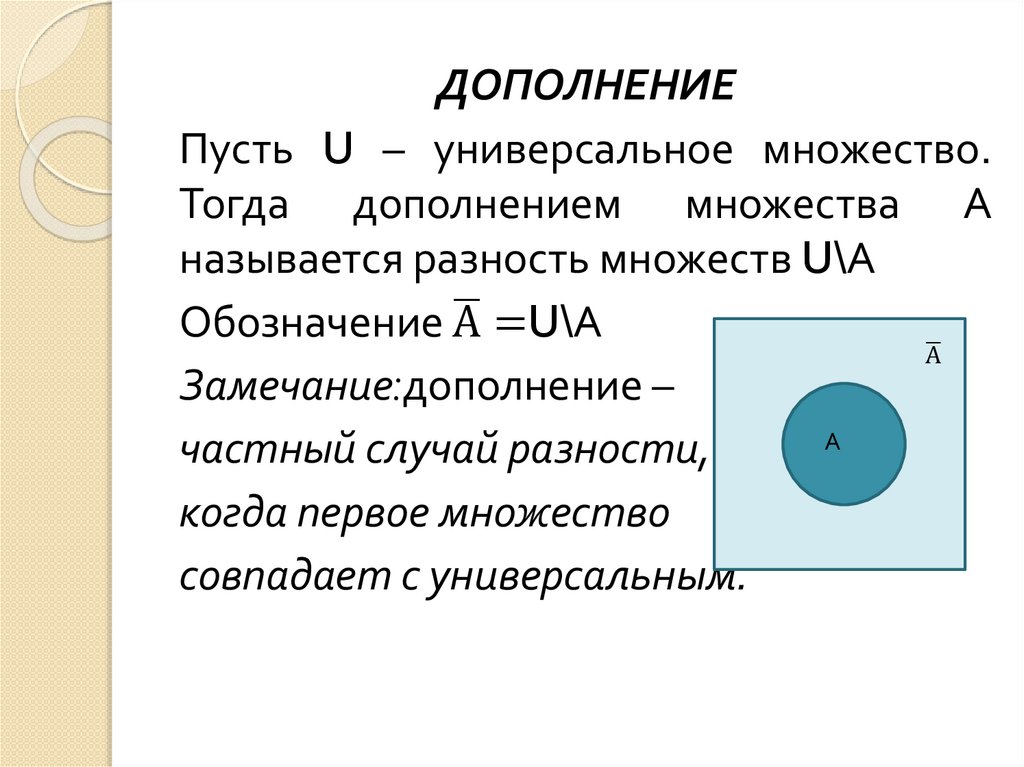
ДОПОЛНЕНИЕПусть U – универсальное множество.
Тогда дополнением множества А
называется разность множеств U\А
ഥ =U\А
Обозначение А
ഥ
А
Замечание:дополнение –
А
частный случай разности,
когда первое множество
совпадает с универсальным.
20.
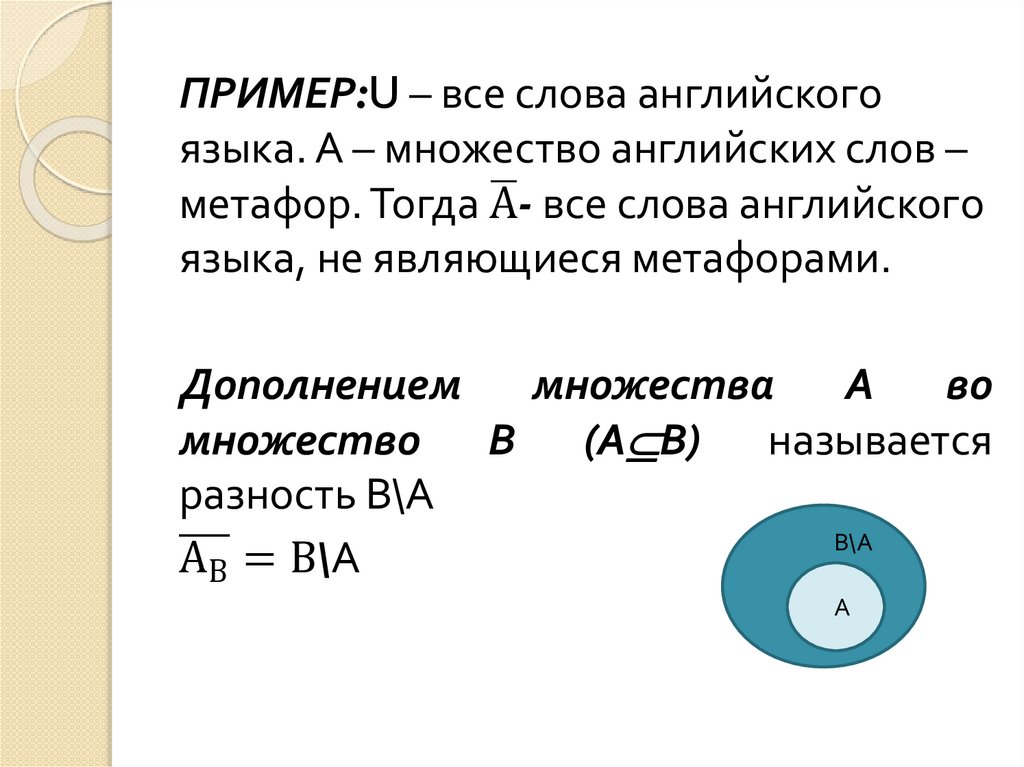
ПРИМЕР:U – все слова английскогоязыка. А – множество английских слов –
ഥ- все слова английского
метафор. Тогда А
языка, не являющиеся метафорами.
Дополнением
множества
А
во
множество В (А В) называется
разность В\А
В\А
АВ = В\А
А
21.
ПРЯМОЕ ИЛИ ДЕКАРТОВОПРОИЗВЕДЕНИЕ МНОЖЕСТВ
Упорядоченной
парой
называется
двухэлементное множество, в котором
строго указано, какой элемент считать
первым, какой – вторым.
Обозначение: (a, b).
Прямым или декартовым произведением
множеств А и В называется множество
А В={(a, b)/ a A, b B}, состоящее из всех
упорядоченных пар, у которых первый
элемент из множества А, а второй – из
множества В}
22.
ПРИМЕР:А={умный,
красивый,
успешный, счастливый}, В={добрый,
веселый}
А В={(умный,
добрый),
(умный,
веселый),
(красивый,
добрый),
(красивый,
веселый),
(успешный,
добрый),
(успешный,
веселый),
(счастливый, добрый), (счастливый,
веселый)}
23.
Число элементов объединения, разности и декартовапроизведения двух конечных множеств
Пусть А и В – конечные множества.
m(A) – число элементов множества А
m(B) – число элементов множества В
А В=
m(A B)=m(A)+m(B)
m(A\B)=m(A)
A
B
24.
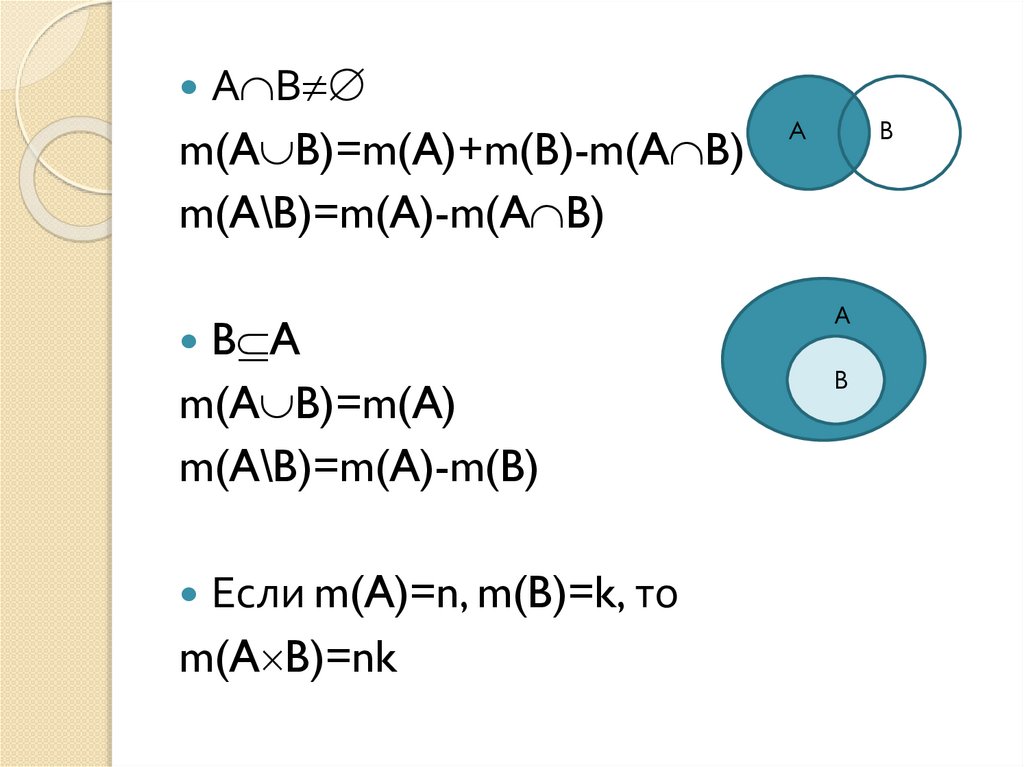
А Вm(A B)=m(A)+m(B)-m(A B)
m(A\B)=m(A)-m(A B)
B A
m(A B)=m(A)
m(A\B)=m(A)-m(B)
Если m(A)=n, m(B)=k, то
m(A B)=nk
A
B
А
B
25.
ПРИМЕР: В классе 25 человек. Из них 15 человекпосещают спецкурс по английскому языку, 14
человек посещают спецкурс по немецкому
языку, 6 человек не ходят на спецкурсы. Сколько
человек посещает два спецкурса?
РЕШЕНИЕ:
U- множество учеников
А – множество учеников, посещающих спецкурс
по английскому языку
В - множество учеников, посещающих спецкурс
по немецкому языку
С – множество учеников, не посещающих
спецкурсы
D – множество учеников, посещающих два
спецкурса
26.
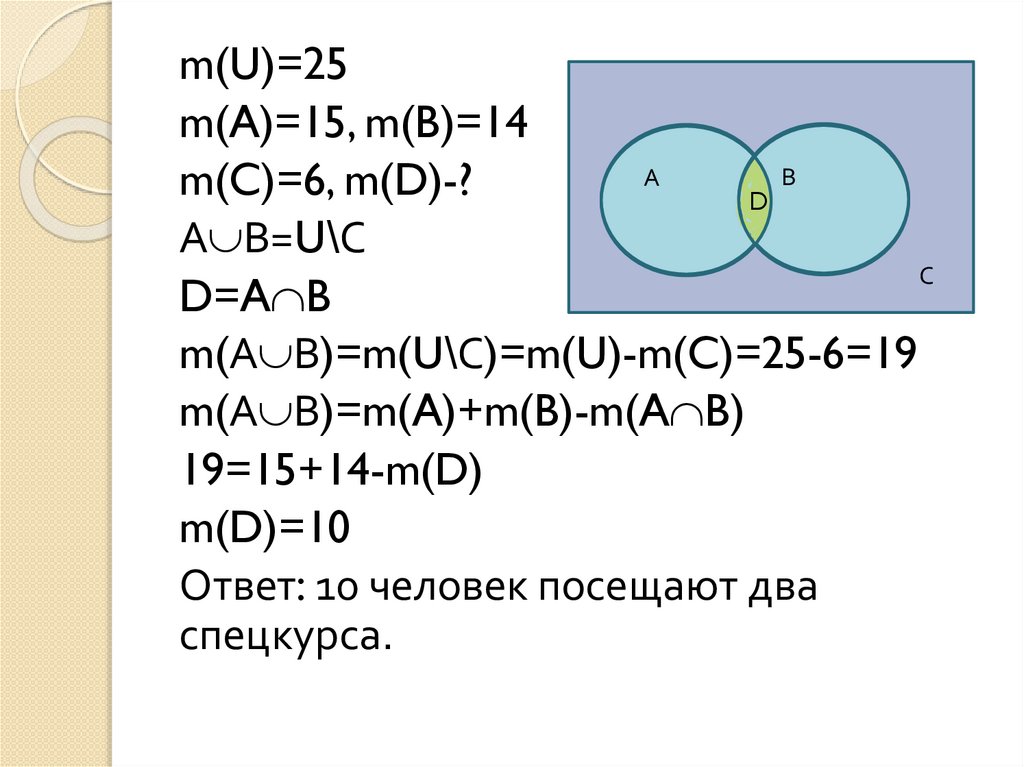
m(U)=25m(A)=15, m(B)=14
В
А
m(C)=6, m(D)-?
D
А В=U\С
С
D=A B
m(А В)=m(U\С)=m(U)-m(C)=25-6=19
m(А В)=m(A)+m(B)-m(A B)
19=15+14-m(D)
m(D)=10
Ответ: 10 человек посещают два
спецкурса.


















 Математика
Математика








