Деревья и их простейшие свойства

1.

Деревья и их
простейшие свойства
Данилов Д.А. 2ИС

2.

Деревом называется связный граф без контуров
(а значит, и без циклов). Граф (несвязный), состоящий
из нескольких деревьев иногда называют лесом.
Напомним, что вершина в графе называется
висячей, если ее степень равна единице.
Дерево должно обязательно иметь висячую
вершину, так, как если бы степень всех вершин
в дереве была бы больше или равна 2, то по
самой первой лемме граф должен иметь цикл,
что противоречит определению дерева.

3.

Теорема. Если граф G является деревом, то число его ребер (т)
и число его вершин (п) связаны соотношением т = п – 1.
На самом деле верно и обратное утверждение, которое
является частью более общей теоремы, отражающей
простейшие свойства дерева.
Теорема. Следующие 4 условия
равносильны:
граф G является деревом;
число ребер (т) и число
вершин в графе (п) связаны
соотношением т = п – 1;
любые две вершины в графе
могут быть связаны (простым)
путем, и этот путь единствен;
граф G связен и не содержит контуров.

4.

Деревья
Связные графы, в которых существует одна и только одна цепь,
соединяющая каждую пару вершин, называются деревьями. Дерево
можно определить и как связный граф, не содержащий циклов.
Пример. Кубок по настольному теннису разыгрывается по
олимпийской системе. Встречи проводятся без "ничьих".
К очередному туру допускается только победившая в предыдущем туре команда.
Проигравшие команды выбывают из игры. Для завоевания кубка команда должна
победить во всех турах. На участие в розыгрыше кубка поданы заявки от 16 команд.

5.

Непосредственно с него считываются:
1.
Число всех участников розыгрыша кубка (число вершин нижнего "яруса").
2.
Число этапов проведения розыгрыша (число "ярусов" из вершин в дереве, не
считая нижнего).
3.
Число команд, участвующих в 1/8 финала, в 1/4 финала, в 1/2 финала (число
вершин, соответственно, в четвертом сверху ярусе, в третьем сверху ярусе, во втором
сверху ярусе).
4.
Число матчей, которые придется сыграть командам для выявления обладателя
кубка (число вершин в графе без нижнего "яруса"). Хотя это число легко определяется и
без дерева. (В каждом матче выбывает одна команда. Для того чтобы была выявлена
команда-победительница, остальные должны выбыть из соревнования. Поэтому число
матчей равно числу команд без одной, а именно 15).

6.

Удобно считать, что граф, состоящий из одной изолированной вершины,
тоже является деревом. Для каждой пары вершин дерева существует
единственный соединяющий их путь. Лесом называется несвязный граф,
представляющий объединение деревьев. Всякое ребро в дереве и в лесе
является мостом (признак 3).

7.

Артур Кэли

8.

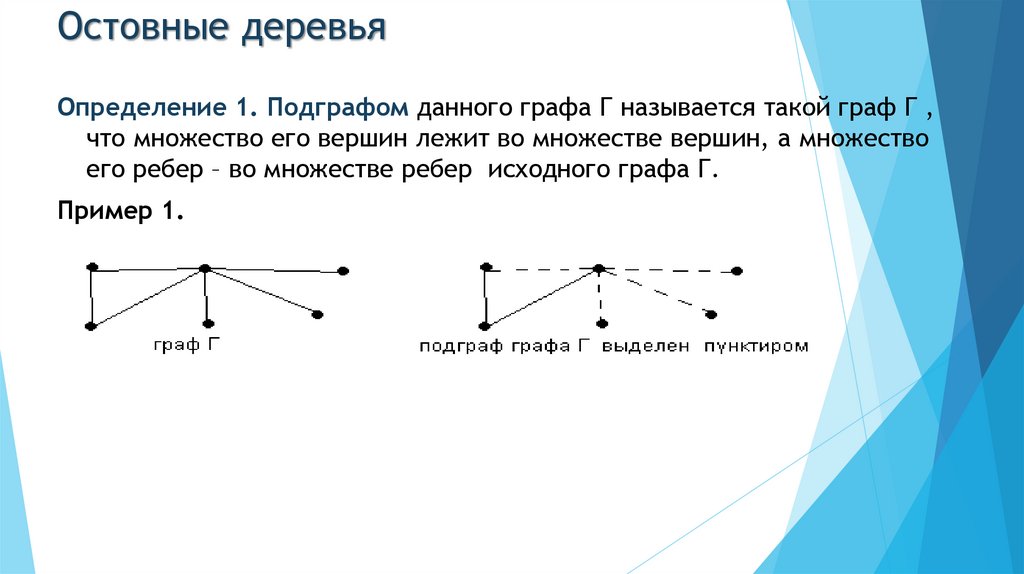
Остовные деревья
Определение 1. Подграфом данного графа Г называется такой граф Г ,
что множество его вершин лежит во множестве вершин, а множество
его ребер – во множестве ребер исходного графа Г.
Пример 1.

9.

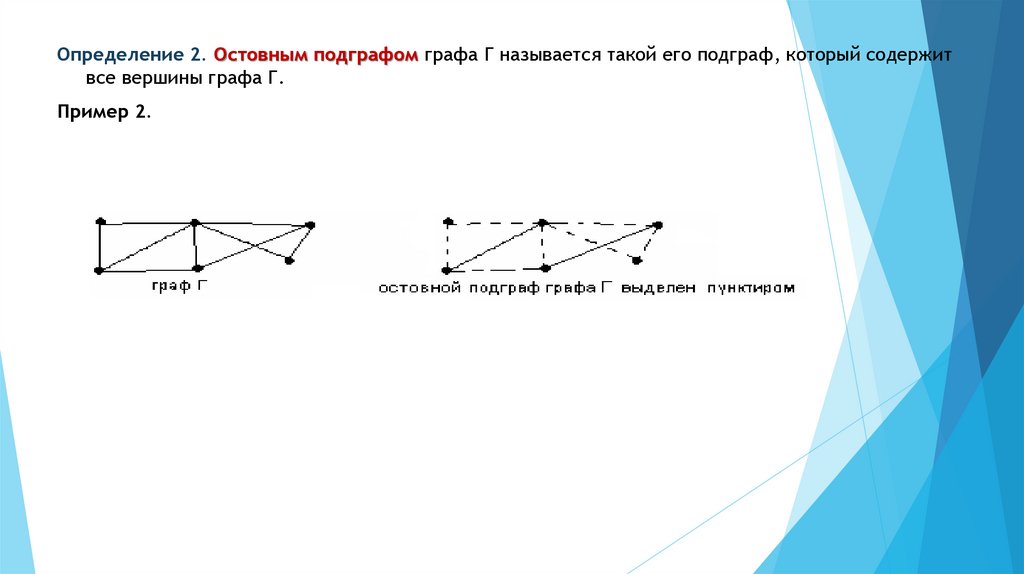
Определение 2. Остовным подграфом графа Г называется такой его подграф, который содержит
все вершины графа Г.
Пример 2.

10.

Определение 3. Остовной подграф, являющийся деревом, называется
остовным деревом.
Пример 3.

11.

Алгоритм построения остовного дерева
графа G
Выбираем в графе G произвольную вершину v1, которая образует подграф
G1 , являющийся деревом. i=1
Если i=n, n- число вершин, то задача решена и Gi – искомое остовное
дерево. Иначе переходим к шагу 3.
Строим граф Gi+1,добавляя к графу Gi новую вершину vi+1 смежную в G с
некоторой вершиной vj графа Gi , и ребро
(vi+1 , vj). Присваиваем i=i+1 и и переходим к шагу 2.

12.

Задачи А. Кэли.
Необходимо соединить n городов железнодорожными линиями так, чтобы
не строить лишних дорог. Известна стоимость строительства для
каждой пары городов. Какова должна быть сеть дорог, соединяющая
все города и имеющая минимальную возможную стоимость?
В терминах теории графов. Рассмотрим граф Г, в котором вершины –
города, ребра – соединяющие пару городов дороги. Каждому ребру
назначим вес – стоимость строительства дороги на этом участке.
Нужно построить связный граф, содержащий все вершины, с
минимальным весом.
Очевидно, что этот граф должен быть деревом – в противном случае,
можно было бы удалить одно ребро, не нарушая связности и уменьшая
сумму весов его ребер.

13.

Деревья в теории вероятностей
Задача
В урне 2 белых и 4 черных шара. Один азартный человек держит пари с другим, что среди
вынутых 3-ех шаров будет ровно 1 белый. В каком отношении находятся шансы спорящих?
Решение (традиционное).
Испытание - вынимание трех шаров.
Событие «А»- достать ровно один белый и два черных шара.
C 63
Число всех исходов
6!
20
3!(6 3)!
Один белый шар можно достать в С21 случаях , а два черных - С42 , тогда по основному правилу
A C21 C42 12
комбинаторики
12
3
Отсюда Р(А)= 20 5
3
2
следовательно Р(A) = 1 - Р( А) = 1 - 5
5
Ответ: отношение шансов спорящих равно 3:2.

14.

Деревья в теории вероятностей
Решение (наглядное)

15.

Деревья в теории вероятностей
Задача
Слово «МАТЕМАТИКА» разделено на отдельные буквы, из них
произвольным образом отбираются и выкладываются по порядку четыре
буквы. Какова вероятность получения слова «МАМА»?
Решение. Составим вероятностное дерево исходов.
Корневая вершина-начало испытания.
Вес ребра - вероятность появления следующей буквы
«А»- вероятность получения слова «МАМА».
2 3 1 2
1
P ( A)
10 9 8 7
420