Прикладная механика. Лекция 4. Сопротивление материалов

1. Прикладная механика Раздел: Сопротивление материалов

Лекция 4
Преподаватель: доцент,
Кандидат технических наук,
Костюк Елена Геннадиевна

2.

Связь между модулем сдвига и модулем упругости при растяжении
– Модуль сдвига и модуль упругости при растяжении являются
физическими постоянными материала, характеризующими жесткость в
каждом из этих двух видов деформации. Поскольку удлинение диагонали
элемента, вызванное сдвигом, может быть получено также растяжением
этого волокна под действием нормальных напряжений, эти константы
должны быть связаны между собой некоторым соотношением:
Удлинение диагонали элемента вследствие деформации сдвига (dy = dz):
■
ds y cos 45 .
0
ds dy cos 45 0.
ds (ds cos 45 0 ) cos 45 0 ds cos 2 45 0.
Удлинение диагонали элемента
ds ds cos 2 45 0
ds.
вследствие деформации растяжения
G
2G
(σ1 = , σ3 = - ):
ds 1
1
(1 )
1
( 1 23 ) ( ( ))
.
ds
E
E
E
(1 )
ds
ds.
E
(1 )
1
.
E
2G
Таким образом существует соотношение
между модулем сдвига и модулем
упругости при растяжении с участием
коэффициента Пуассона.
E
G
.
2(1 )

3. Напряжения при кручении

max
T
Ip
Полярный момент инерции характеризует, влияние
размеров и форма поперечного сечения вала на его
способность сопротивляться угловым деформациям
d
d /2
2 3 d I p
0
d 1
Для
круглого
Для трубчатого
Ip
,
Ip
сечения
32
сечения
32
здесь a = d1 /d, d1 –внутренний диаметр трубы, d – наружный диаметр трубы
Полярный момент инерции выражается в м4 (мм4, см4).
I
Полярный момент сопротивления характеризует влияние геометри- W p p
макс
ческих размеров и формы поперечного сечения вала на его прочность.
d 3 Для круглого
d 3 1 4 Для трубчатого
Wp
Wp
сечения
сечения
16
16
4
4
4
Максимальные касательные напряжения max прямо
пропорциональны крутящему моменту T в опасном сечении
и обратно пропорциональны полярному моменту
сопротивления сечения Wp:
T
max
Wp

4.

5. Условие прочности при кручении

Наибольшие касательные напряжения, возникающие в
скручиваемом брусе не должны превышать соответствующих
допускаемых значений
по 3 теории
кр
прочности
Tмакс
2
кр Допускаемые
по 4 теории
Wp
напряжения
кр
3 прочности
Из условия прочности вытекает три типа задач при кручении
16Tм акс
Для круглого
d 3
1. Задача проектного
расчета
р
16Tмакс
d 3
1 4 р
2. Задача проверочного
расчета
3. Определение
допускаемого момента
Tмакс
кр
Wp
T кр W p
сечения
Для трубчатого
сечения

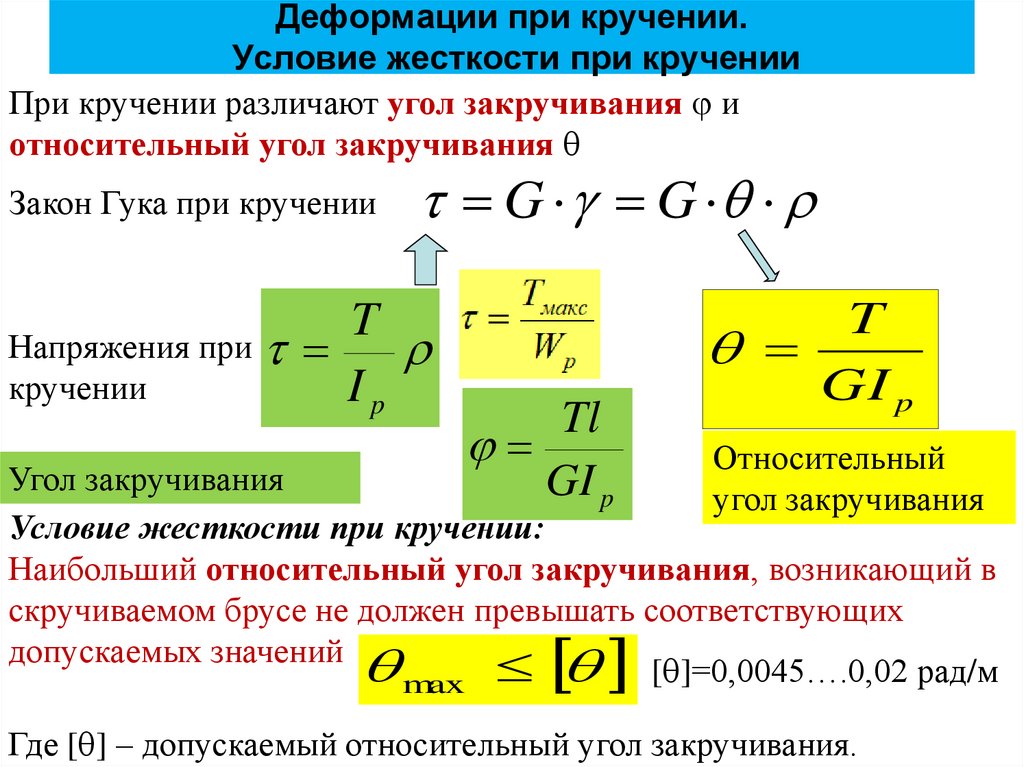
6. Деформации при кручении. Условие жесткости при кручении

При кручении различают угол закручивания и
относительный угол закручивания
Закон Гука при кручении
G G
T
Напряжения при
кручении
Ip
Tl
GI p
T
GI p
Относительный
угол закручивания
Угол закручивания
Условие жесткости при кручении:
Наибольший относительный угол закручивания, возникающий в
скручиваемом брусе не должен превышать соответствующих
допускаемых значений
max [ ]=0,0045….0,02 рад/м
Где [ ] – допускаемый относительный угол закручивания.

7. Потенциальная энергия деформации

2
T
T
Tl
T
l
Полная потенциальная
U
энергия деформации
2
2 GI p 2GI p
Удельная потенциальная энергия (полная)
1
u
12 22 32 2 1 2 2 3 1 3
2E
(σ1 = , σ3 = - )
1
1 2
2
2
u
2 2
2E
E
Удельная потенциальная энергия
изменения объема
Удельная потенциальная энергия изменения
формы
1 2
1 2 2
2
2
2
2
u
uV
1 2 3 ф
1
2
3 1 2 2 3 3 1
3Е
6E
1
1 2 2 2 3 2 3 1 2
6Е
При кручении
1 ;
2 0;
3

8.

Изгиб
Под изгибом понимают такой вид деформации, при которой в
поперечном сечении бруса действует изгибающий момент, от
действия последнего происходит искривление оси бруса.
Различают два вида плоского изгиба: чистый и поперечный изгиб.
Под плоским чистым изгибом
понимают деформацию, когда в
поперечных сечениях участка бруса
действует только один силовой
фактор отличный от нуля и
одинаковый во всех сечениях – это
изгибающий момент
F2
F1
RB
RA
М
А
М
В
F2
F1
Q
RB
RA
М
М
В
А
Q
Под плоским поперечным изгибом
понимают такой вид деформации,
при которой в поперечном сечении
бруса действует два силовых
фактора: изгибающий момент М и
поперечная сила Q

9.

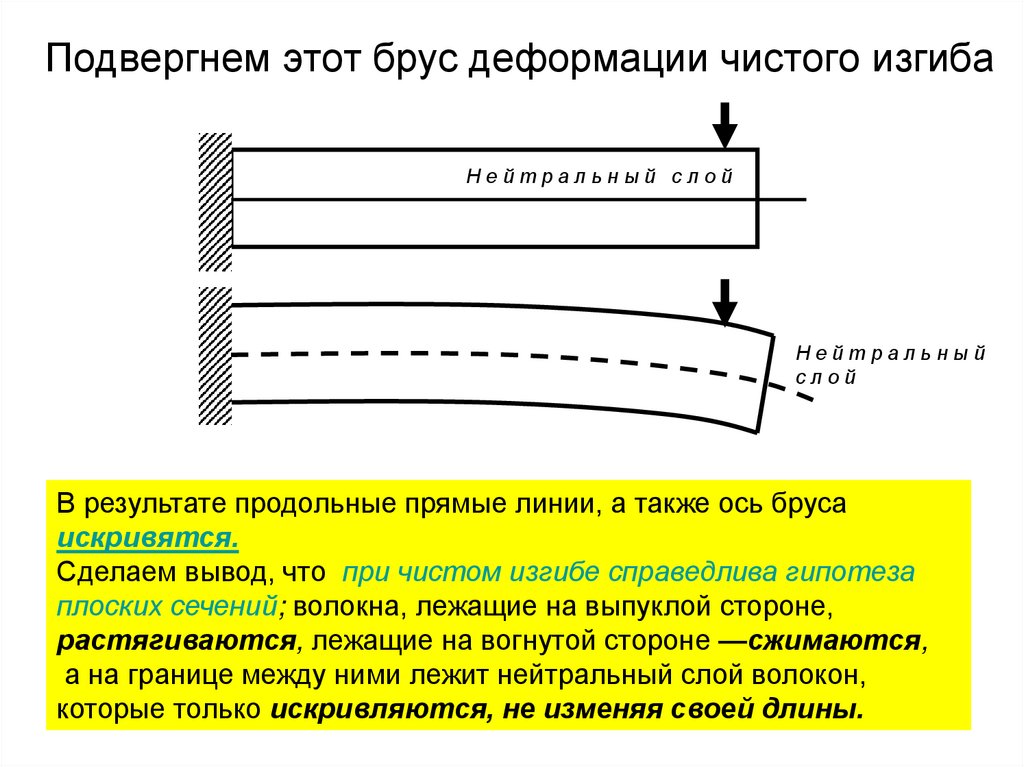
Подвергнем этот брус деформации чистого изгиба
Нейтральный слой
Нейтральный
слой
В результате продольные прямые линии, а также ось бруса
искривятся.
Сделаем вывод, что при чистом изгибе справедлива гипотеза
плоских сечений; волокна, лежащие на выпуклой стороне,
растягиваются, лежащие на вогнутой стороне —сжимаются,
а на границе между ними лежит нейтральный слой волокон,
которые только искривляются, не изменяя своей длины.

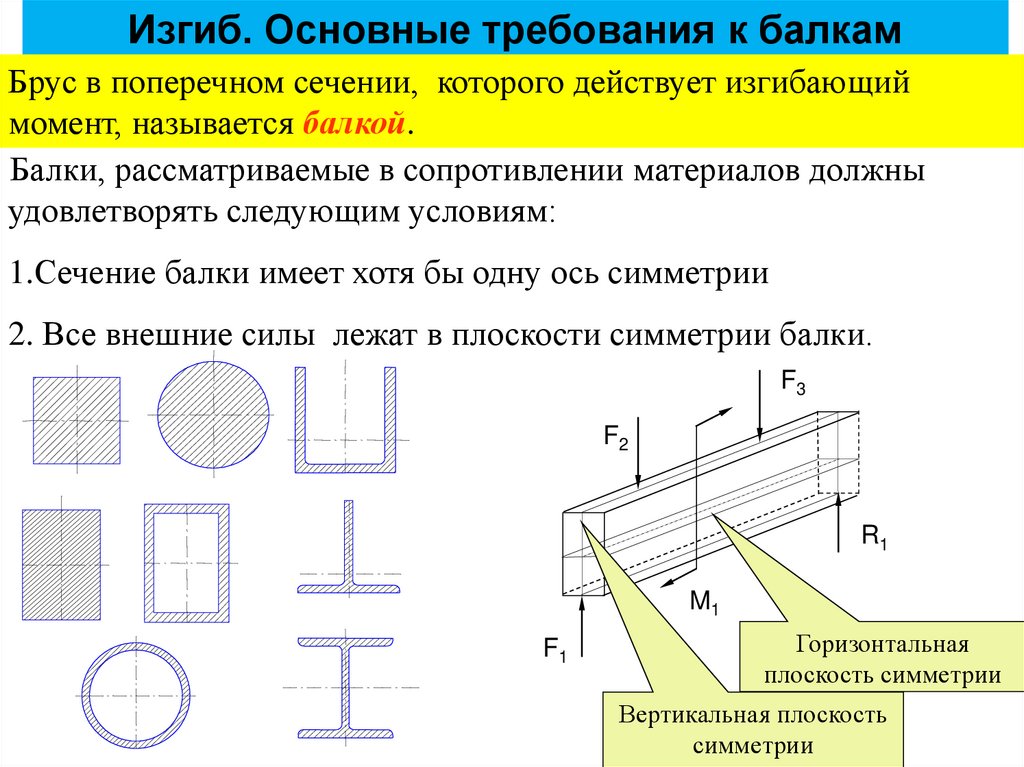
10. Изгиб. Основные требования к балкам

Брус в поперечном сечении, которого действует изгибающий
момент, называется балкой.
Балки, рассматриваемые в сопротивлении материалов должны
удовлетворять следующим условиям:
1.Сечение балки имеет хотя бы одну ось симметрии
2. Все внешние силы лежат в плоскости симметрии балки.
F3
F2
R1
M1
F1
Горизонтальная
плоскость симметрии
Вертикальная плоскость
симметрии

11. Правило знаков для внутренних силовых факторов

Поперечная сила считается положительной, если равнодействующая внешних сил, приложенная слева от выбранного сечения
направлена вверх и отрицательной, если она направлена вниз.
Изгибающий момент условимся считать в сечении
положительным, если внешняя нагрузка, приложенная к
рассматриваемой отсеченной части, приводит к растяжению в
данном сечении нижних волокон балки и отрицательной - в
противном случае.
Положительная поперечная сила
Q
Q
Отрицательная поперечная сила
Q
Q
Положительный момент
М
М
Отрицательный момент
М
М

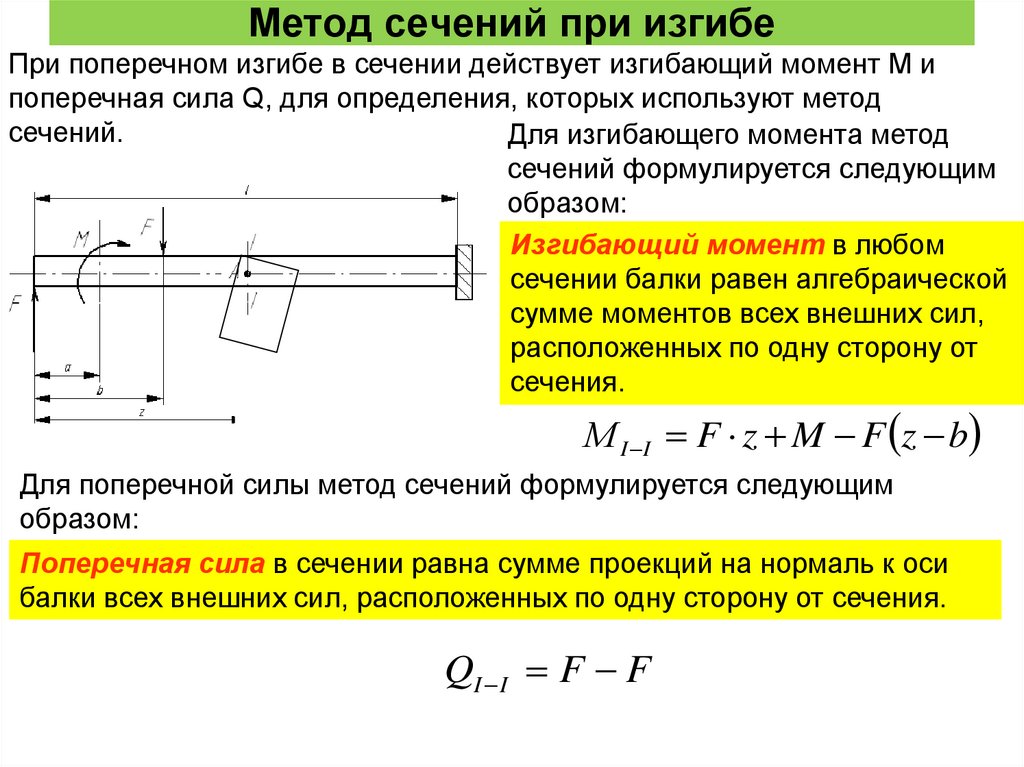
12. Метод сечений при изгибе

При поперечном изгибе в сечении действует изгибающий момент М и
поперечная сила Q, для определения, которых используют метод
сечений.
Для изгибающего момента метод
сечений формулируется следующим
образом:
Изгибающий момент в любом
сечении балки равен алгебраической
сумме моментов всех внешних сил,
расположенных по одну сторону от
сечения.
М I I F z M F z b
Для поперечной силы метод сечений формулируется следующим
образом:
Поперечная сила в сечении равна сумме проекций на нормаль к оси
балки всех внешних сил, расположенных по одну сторону от сечения.
QI I F F

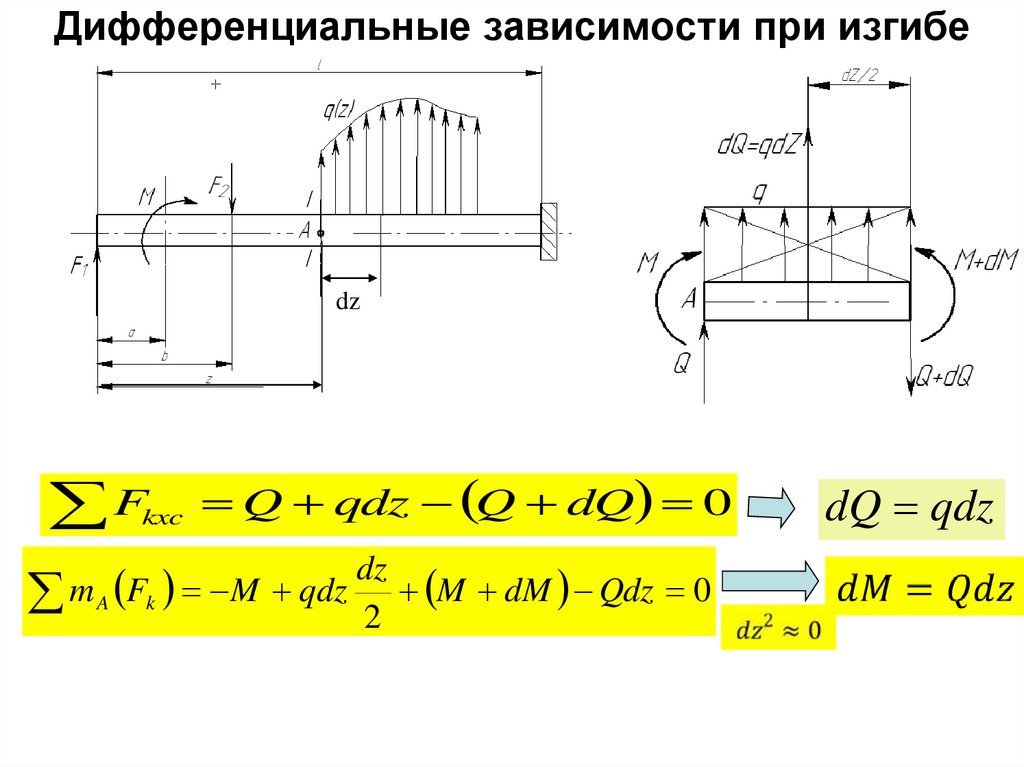
13. Дифференциальные зависимости при изгибе

dz
F
kxc
Q qdz Q dQ 0
dz
m A Fk M qdz 2 M dM Qdz 0
dQ qdz

14. Дифференциальные зависимости при изгибе

Fkxc Q qdz Q dQ 0
dz
m A Fk M qdz 2 M dM Qdz 0
Первая производная от поперечной силы по
длине балки равна интенсивности
распределенной нагрузки, перпендикулярной к ее
оси.
Первая производная от изгибающего момента
по длине балки равна поперечной силе.
dQ
q
dz
dM
Q
dz
2
dQ d M
q
dz
dz 2
Вторая производная от изгибающего
момента по длине балки равна
интенсивности распределенной нагрузки,
перпендикулярной к ее оси.

15.

Правила контроля эпюр
а
RB
R
A
а
b
F
R
A
b
F
R
B
F
RB
F
RA
RB
RA
RA
a
RA
a
1. В сечении, в котором к балке приложена сосредоточенная внешняя
сила, перпендикулярная к оси балки эпюра поперечных сил Q делает
скачок на величину этой силы и с ее знаком.
2. В сечении, где приложена сосредоточенная внешняя сила эпюра изгибающих
моментов делает резкое изменение угла наклона смежных участков эпюры (излом
эпюры). Излом эпюры направлен навстречу вектору силы.

16.

а
b
RA
R
M
RA
B
R
B
RA
a
M
q
R
A
l
R
В
RA
2
q l /8
RB
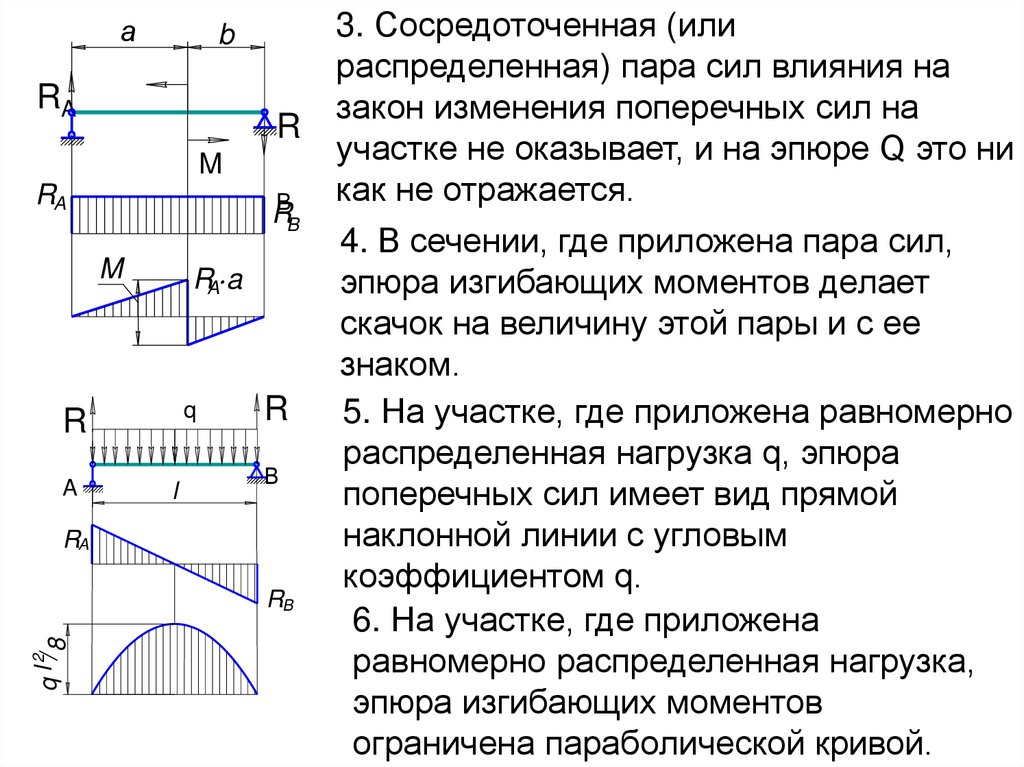
3. Сосредоточенная (или
распределенная) пара сил влияния на
закон изменения поперечных сил на
участке не оказывает, и на эпюре Q это ни
как не отражается.
4. В сечении, где приложена пара сил,
эпюра изгибающих моментов делает
скачок на величину этой пары и с ее
знаком.
5. На участке, где приложена равномерно
распределенная нагрузка q, эпюра
поперечных сил имеет вид прямой
наклонной линии с угловым
коэффициентом q.
6. На участке, где приложена
равномерно распределенная нагрузка,
эпюра изгибающих моментов
ограничена параболической кривой.

17.

а
RA
a
а
F
l
RA
F
a
F
F
RB
RB
RA
F
RA
RB
RB
RA
a
RA
a
RB
a
7. На участке, где поперечная сила равна нулю, наблюдается деформация
чистого плоского изгиба, при котором изгибающий момент является
постоянной величиной (М=const).

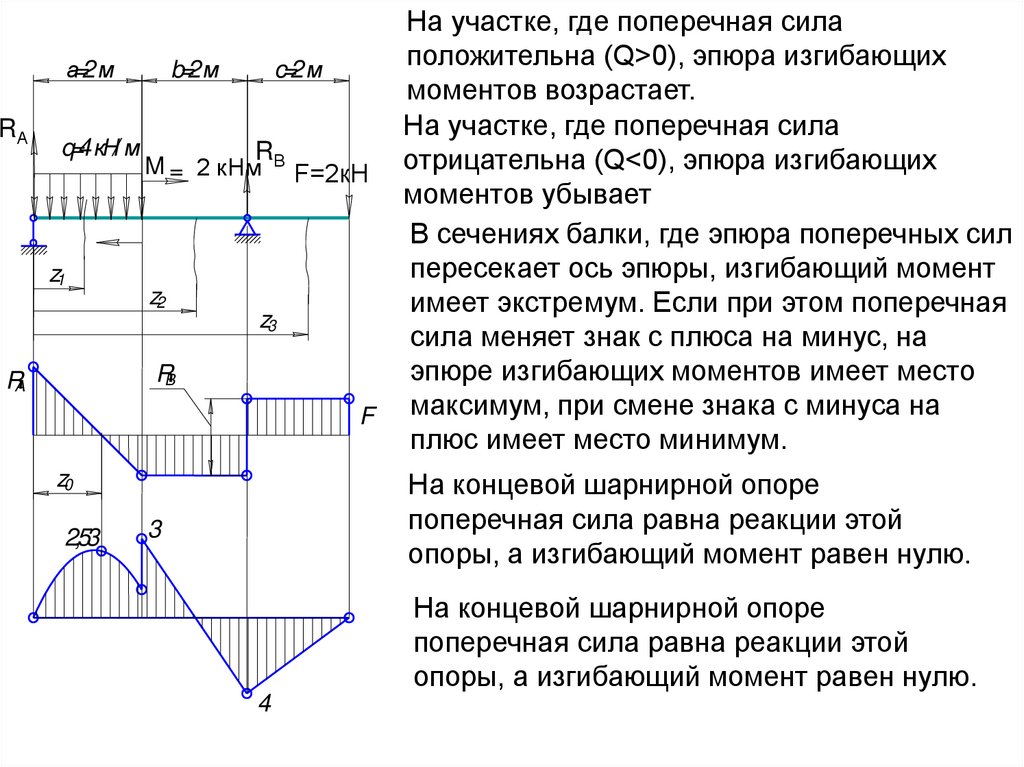
18. Порядок построения эпюр Q и М

а=2 м
RA
b=2 м
q=4 кН/ м
M=2кНм
1. Определяем реакции опор
c=2 м
Сумма моментов всех сил относительно
опоры В:
m F R a b qa a / 2 b M Fc 0
RB
B
F=2кН
RA
k
A
Реакция в опоре А:
qa a / 2 b M Fc 4 2 1 2 2 2 2
4,5 кН
a b
2 2
Сумма моментов всех сил относительно опоры А:
m F R a b qa a / 2 b M Fc 0
À
k
Â
Реакция в опоре В:
qa a / 2 M F a b c 4 2 1 2 2 6
RB
5,5
4,5кНкН
a b
2 2
Проверка:
F R qa R F 4,5 4 2 5,5 2 0
ky
A
B

19.

а=2 м
b=2 м
2. Разбиваем балку на участки
c=2 м
Уравнения для поперечной силы
RA q = 4 кН/ м M 2 кНм
=
RB
F=2к
Н
z1
z2
z3
F
z0
Q1=RA-q z1
Прямая наклонена оси эпюры
при z1=0, Q1=RA-=4,5 кН;
при z1=2 м, Q1(2)=RA-qz=4,5-4∙2=3,5 кН.
Координаты сечения в котором поперечная
сила равна нулю:
RB
RA
1 участок 0≤z1≤a=2 м.
Q1=RA-q z0 =0,
z 0=RA/q=4,5/4=1,125 м
2 участок 2 м ≤z2≤a=4 м.
Q2=RA-q а Прямая параллельная оси эпюры
при z2=2, Q2(2)=RA-2q=4,5-4∙2=-3,5 кН;
3 участок 4 м ≤z3≤a=6 м.
Q3=RA-q а+RB
Прямая параллельная оси эпюры
при z3=4, Q3(4)=RA-2q + RB =4,5-4∙2+5,5=2 кН;

20.

а=2 м
b=2 м
1 участок 0≤z1≤2 м
RA q=4 кН/ м
z1
Уравнения для изгибающего момента
c=2 м
M=2кНм
z2
RB
F=2 к Н
При z1=0, M1(0)=0. Квадратная парабола
При z1=z0=1,125 м
z3
M1(1,125)=4,5∙1,125-4∙1,1252/2=2,53 кН∙м.
RB
RA
M1=RA∙z1 -q∙z12/2
F
При z1=2 м, М1(2)=4,5∙2-4∙22/2=1 кН∙м;
z0
2,53
3
2 участок 2≤z2≤4 м
M2=RA∙z2 -q∙a∙(z2-a/2)+М Убывающая наклонная прямая
1 к∙Нм
При z2=2, M2(2)=4,5∙2-4∙2(2-1)+2=3 кН∙м.
4
При z2=4 м M2(4)=4,5∙4-4∙2(4-1)+2=-4 кН∙м.
3 участок 4≤z3≤6 м
M3=RA∙z3 - q∙a∙(z3-a/2) + М + RB(z3-4)
Возрастающая наклонная прямая
При z3=4 м M3(4)=4,5∙4-4∙2(4-1)+2 =-4 кН∙м;
При z3=6 м М3(6)=4,5∙6-4∙2(6-1)+2+5,5(6-4)=0

21.

а=2 м
RА
q=4 кН/ м
z1
b=2 м
c=2 м
R
M = 2 кНм В F=2кН
z2
z3
RB
RA
F
На концевой шарнирной опоре
поперечная сила равна реакции этой
опоры, а изгибающий момент равен нулю.
z0
2,53
На участке, где поперечная сила
положительна (Q>0), эпюра изгибающих
моментов возрастает.
На участке, где поперечная сила
отрицательна (Q<0), эпюра изгибающих
моментов убывает
В сечениях балки, где эпюра поперечных сил
пересекает ось эпюры, изгибающий момент
имеет экстремум. Если при этом поперечная
сила меняет знак с плюса на минус, на
эпюре изгибающих моментов имеет место
максимум, при смене знака с минуса на
плюс имеет место минимум.
3
На концевой шарнирной опоре
поперечная сила равна реакции этой
опоры, а изгибающий момент равен нулю.
4

22.

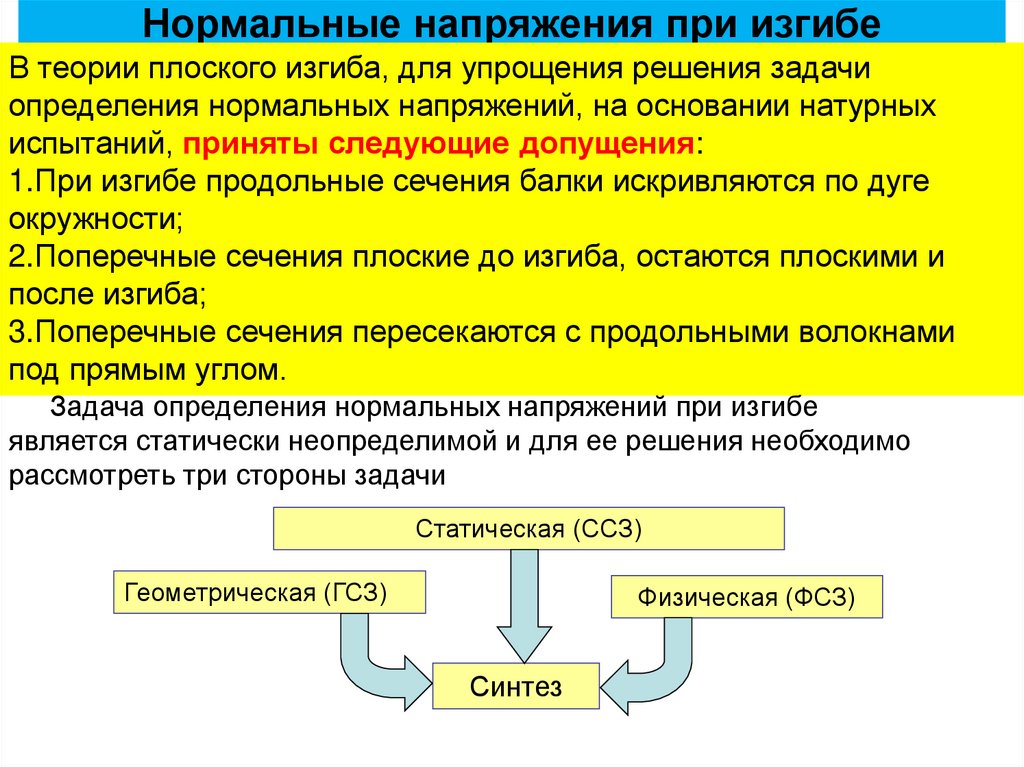
Нормальные напряжения при изгибе
В теории плоского изгиба, для упрощения решения задачи
определения нормальных напряжений, на основании натурных
испытаний, приняты следующие допущения:
1.При изгибе продольные сечения балки искривляются по дуге
окружности;
2.Поперечные сечения плоские до изгиба, остаются плоскими и
после изгиба;
3.Поперечные сечения пересекаются с продольными волокнами
под прямым углом.
Задача определения нормальных напряжений при изгибе
является статически неопределимой и для ее решения необходимо
рассмотреть три стороны задачи
Статическая (ССЗ)
Геометрическая (ГСЗ)
Физическая (ФСЗ)
Синтез

23. Статическая сторона задачи

1 участок
2 участок
3 участок
а
l
a
RB
RA
F
z1
Опорные реакции
m F F a l R l Fa 0
mB Fк F (a l ) RAlB Fa 0
A
к
B
F a l Fa
F a l Fa
F RB
F
l
F
l
Проверка Fкy F RA RB F F F F F 0
RA
Эпюры поперечных сил и изгибающих моментов
z2
1 участок 0 ≤ z1 ≥ a
z3
Q1 F
M1 F z1 При z1=0, М1(0)=0
При z1=а, М1(а)=F·a
2 участок a ≤ z2 ≥ (a+l) Q2 F RA F F 0
Эпюра поперечных сил
F
M 2 F z2 F z2 a При z2=а, М2(а)=F·a
При z2=а+l, М2(а+l)=F·(a+l) -F(a+l-a)=Fa
Эпюра изгибающих моментов
Fa
Fa
F
3 участок (a+l) ≤ z3 ≥ (2a+l)
Q3 F RA RB F F F F
M 3 F z3 F z3 a F z3 a l
При z3=а+l, М3(а+l)=F·(a+l) -F(a+l-a)=Fa
При z3=2а+l, М2(2а+l)=F·(2a+l) -F(2a+l-a)=0

24. Статическая сторона задачи

Если к балке приложен положительный изгибающий момент, то в этом случае,
верхние ее волокна укорачиваются, а нижние удлиняются. Длина нейтрального
волокна остается неизменной.
Нейтральный слой
RB
F
x
y
RA
F
y
Нейтральный линия
dA
z
Совокупность волокон, не меняющих своей
длины при изгибе балки, называется
нейтральным слоем.
Линия, по которой поперечное сечение балки
пересекается с нейтральным слоем балки,
называется нейтральной линией сечения.
x
Нейтральный
слой
Мx
Qy dA 0 M x y dA 0 M y x dA 0
A
A
A

25. Геометрическая сторона задачи

Длина отрезка на нейтральном слое
a0b0 dz
Центр
изгиба
Длина отрезка на слое удаленном от
нейтрального на расстояние y
a1b1 y
Удлинение отрезка после деформации
ab a1b1 a0b0 y y
Относительная деформация
dz
F
a0
a1
b0
b1
F
y
a1b1 a0 b0 y
a0 b0

26. Физическая сторона задачи

При чистом изгибе в поперечных сечениях балки действуют единственный
силовой фактор изгибающий момент, поперечные силы отсутствуют, а
следовательно отсутствуют и касательные напряжения.
Под действием нормальных напряжений часть волокон балки удлиняется,
другая часть укорачивается и для них можно записать закон Гука при
растяжении:
a1b1 a0 b0 y
a0 b0
с
y
x
р
Нейтральная
линия
E
E
y

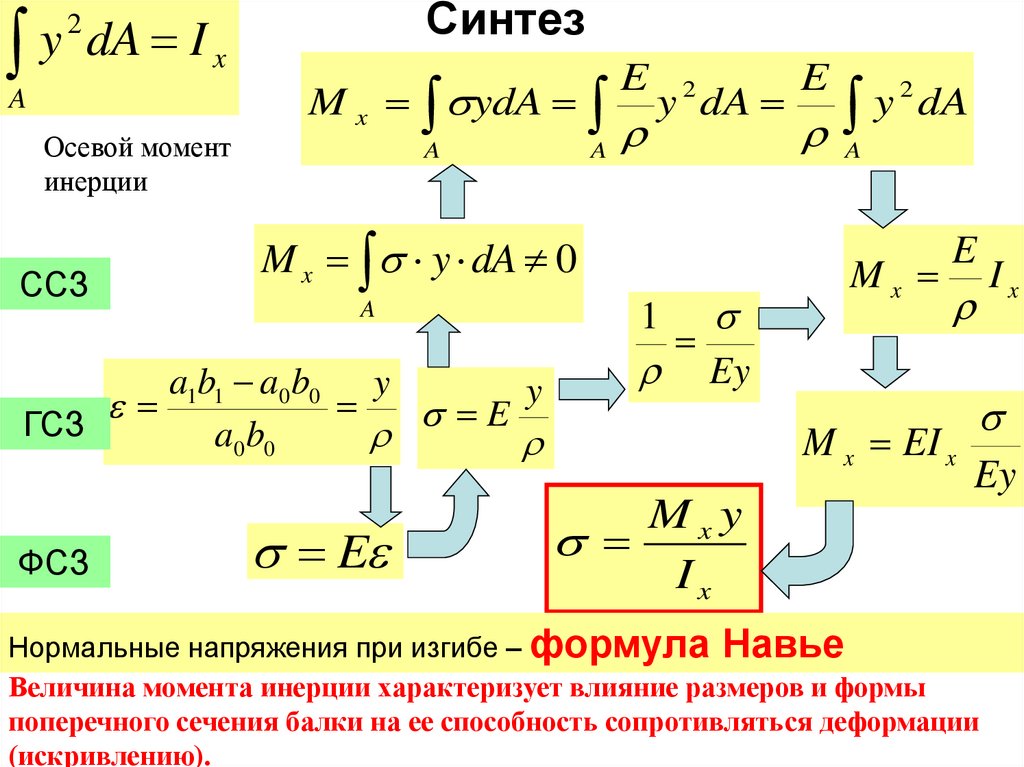
27. Синтез

2
y
dA
I
x
A
Осевой момент
инерции
ССЗ
Синтез
M x ydA
A
M x y dA 0
A
a1b1 a0 b0 y
y
E
ГСЗ
a0 b0
ФСЗ
A
E
E
y dA
2
Ey
1
E
2
y
dA
A
Mx
E
Ix
M x EI x
Ey
Mxy
Ix
Нормальные напряжения при изгибе – формула Навье
Величина момента инерции характеризует влияние размеров и формы
поперечного сечения балки на ее способность сопротивляться деформации
(искривлению).

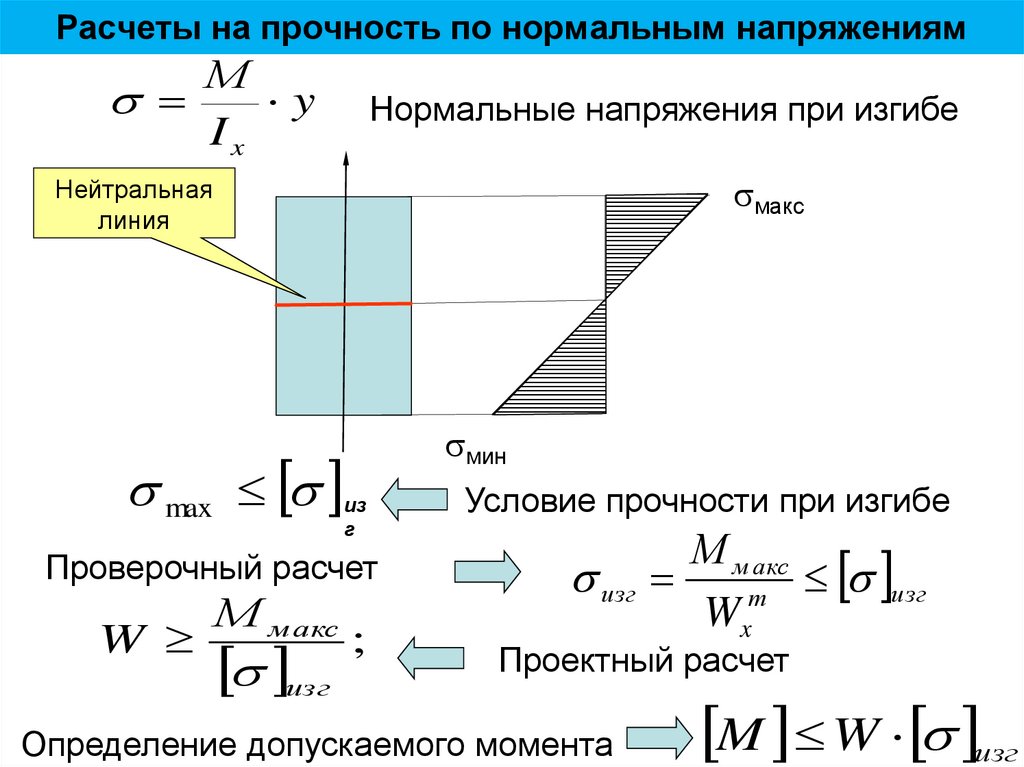
28. Расчеты на прочность по нормальным напряжениям

М
y
Ix
Нормальные напряжения при изгибе
макс
Нейтральная
линия
мин
max
из
г
Проверочный расчет
W
М м акс
изг
;
Условие прочности при изгибе
М м акс
изг
изг
т
Wx
Проектный расчет
Определение допускаемого момента
M W изг

29.

Расчеты на прочность по касательным напряжениям
В общем случае при поперечном изгибе балок произвольного профиля могут
возникать две компоненты полного касательного напряжения в сечении.
Компонента zx для такого сечения не может быть найдена методами
сопротивления материалов. Касательные напряжения zy, возникающие в
поперечном сечении, связаны с поперечной силой, действующей
Qy zy dA.
в этом сечении бруса, интегральной зависимостью:
A
из этого уравнения найти касательные напряжения для
известной поперечной силы нельзя
Выделим малый элемент двумя
нормальными к оси бруса и заменим
действие отброшенных частей
нормальными напряжениями и касательными
напряжениями. Под их действием элемент
находится в равновесии.
При действии поперечной силы изгибающий
момент в сечении, отстоящем на расстоянии
dz от другого сечения, имеет приращение
dMx.
Mx
Ix
Согласно зависимости
нормальные напряжения также
получают приращения:
y
dM x
d
y.
Ix

30.

Отсечем от рассматриваемого элемента некоторую ее часть
горизонтальной плоскостью и заменим ее действие касательными
напряжениями (нормальные напряжения в соответствии с гипотезой об
отсутствии сдавливания продольных волокон не рассматриваются).
Оставшийся элемент по-прежнему находится в равновесии. Уравнение
равновесия в проекции на ось z :
Z i 0; - ( z d z )dA z dA yz dA 0.
Aотс
Aотс
A1
или -
d z dA yz dA 0.
Aотс
A1
Здесь Aотс – площадь отсеченной части
поперечного сечения, A1 – площадь
горизонтального сечения элемента,
равная bdz.
Перенесем первый интеграл в
правую часть и подставим в него
выражение для нормальных
напряжений:
dM
yz dA
A1
Aотс
x
Ix
ydA.

31.

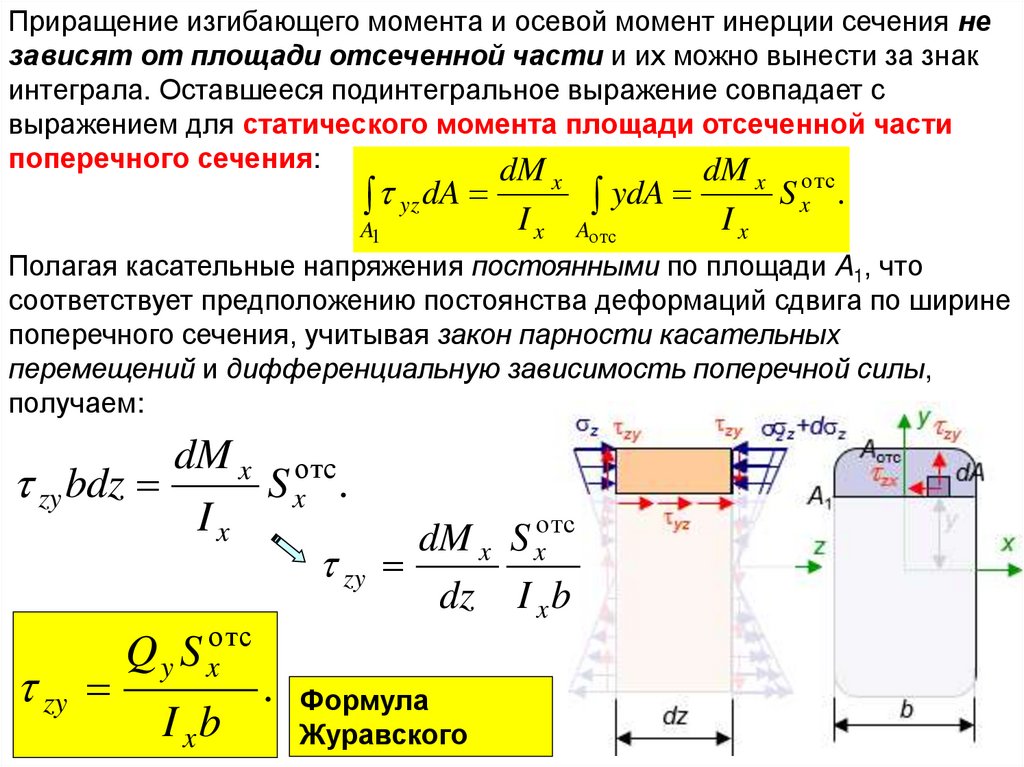
Приращение изгибающего момента и осевой момент инерции сечения не
зависят от площади отсеченной части и их можно вынести за знак
интеграла. Оставшееся подинтегральное выражение совпадает с
выражением для статического момента площади отсеченной части
поперечного сечения:
dM
dM
yz dA
A1
x
Ix
ydA
Aотс
x
Ix
S xотс .
Полагая касательные напряжения постоянными по площади A1, что
соответствует предположению постоянства деформаций сдвига по ширине
поперечного сечения, учитывая закон парности касательных
перемещений и дифференциальную зависимость поперечной силы,
получаем:
dM x отс
zy bdz
Sx .
Ix
dM x S xотс
zy
dz
zy
Q y S xотс
I xb
. Формула
Журавского
I xb

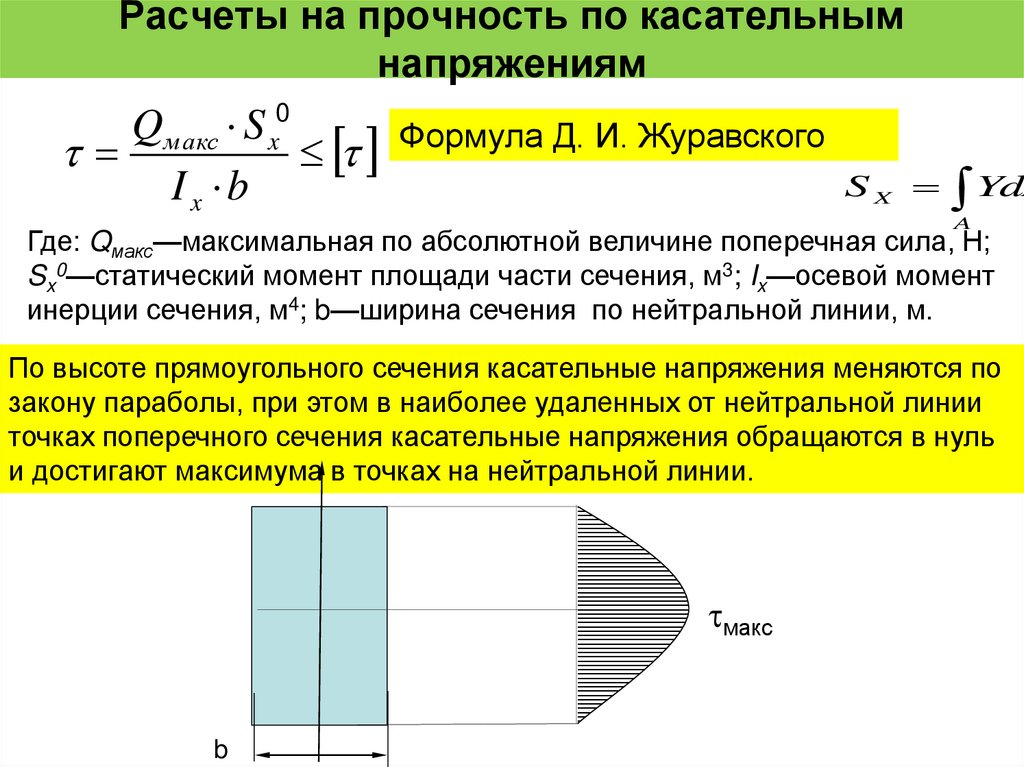
32. Расчеты на прочность по касательным напряжениям

Qм акс S x0
Формула Д. И. Журавского
S X YdA
Ix b
A
Где: Qмакс—максимальная по абсолютной величине поперечная сила, Н;
Sx0—статический момент площади части сечения, м3; Ix—осевой момент
инерции сечения, м4; b—ширина сечения по нейтральной линии, м.
По высоте прямоугольного сечения касательные напряжения меняются по
закону параболы, при этом в наиболее удаленных от нейтральной линии
точках поперечного сечения касательные напряжения обращаются в нуль
и достигают максимума в точках на нейтральной линии.
макс
b

33. Расчеты на прочность при изгибе

При поперечном изгибе материал балки находится в неоднородном
напряженном состоянии. Крайние (наиболее удаленные от
нейтральной линии) точки сечения находятся в линейном
напряженном состоянии и испытывают деформации растяжения
или сжатия. Нейтральное волокно находится в плоском
напряженном состоянии чистого сдвига, а все другие точки
находятся в произвольном плоском напряженном состоянии.
t
1
σ мин
F
мак
2
3
σ маачк
Mмакс =F
4
L
мин
τ
мин
1
τ
мак
мак
τ
τ
2
3

34. Расчеты на прочность при изгибе

Опасной называется точка, где материал
находится в более напряженном состоянии.
1. Опасной может быть наиболее удаленная от
нейтрального слоя точка опасного сечения, где
нормальные напряжения достигают наибольшей
величины;
2. Опасной может быть точка нейтрального слоя
сечения, в котором действует наибольшая
поперечная сила, где касательные напряжения
достигают наибольшей величины;
3. Опасной может быть точка, в которой и τ, хотя и не
принимают наибольших значений, но в своей
комбинации создают наиболее не выгодное
сочетание, то есть в этой точке действуют
наибольшие эквивалентные напряжения.

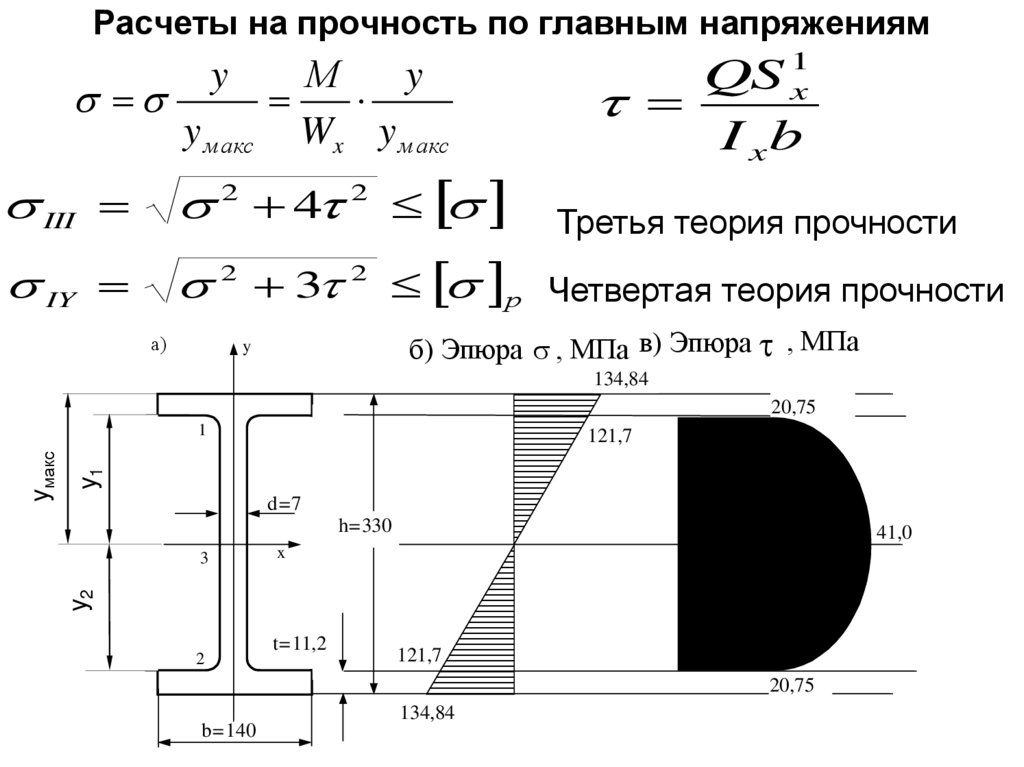
35. Расчеты на прочность по главным напряжениям

М
y
y м акс Wx y м акс
y
QS 1x
I xb
III
2 4 2
IY
2 3 2 р Четвертая теория прочности
а)
Третья теория прочности
б) Эпюра , МПа в) Эпюра , МПа
y
134,84
20,75
y1
121,7
d=7
h=330
3
41,0
x
y2
yмакс
1
2
t=11,2
121,7
20,75
134,84
b=140

36. Перемещения при изгибе

Под расчетом на жесткость понимают оценку упругой податливости балки
под действием приложенных нагрузок и подбор таких размеров
поперечного сечения, при которых перемещения не будут превышать
установленных нормами пределов.
f м акс f
l
Условие жесткости при изгибе
400...800
Перемещение центра тяжести сечения по направлению перпендикулярному к оси балки, называется прогибом.
Прогиб обозначается буквой w
Наибольший прогиб в пролете или на консоли балки, называется стрелой
прогиба и обозначается буквой f.
Угол, , на который каждое сечение поворачивается по отношению к
своему первоначальному положению и есть угол поворота.
Угол поворота считается положительным, при повороте сечения против
хода часовой стрелки
d
Угол поворота сечения равен значению производной от
прогиба по координате Z в этом же сечении, то есть:
dz

37. Уравнение упругой линии балки

d
2
M ( z)
2
EI x
d z
Существуют три метода решения дифференциального
уравнения упругой линии балки. Это метод непосредственного
интегрирования, метод Клебша и метод начальных
параметров.
Метод непосредственного интегрирования
Проинтегрировав уравнение упругой линии балки первый раз,
получают выражение для определения углов поворота:
d
dM ( z )
EI x
EI x ( z )
C
dz
dz
Интегрируя второй раз, находят выражения для определения прогибов:
dM ( z ) 2
EI x ( z )
Cz D
2
d z
Значения постоянных интегрирования С и D определяют из начальных
условий на опорах балки

38. Уравнение упругой линии балки

Метод Клебша
Для составления уравнений необходимо выполнить
следующие основные условия:
•начало координат, для всех участков, необходимо
расположить в крайнем левом конце балки;
•интегрирование дифференциального уравнения упругой
линии балки проводить, не раскрывая скобок;
•при включении в уравнение внешнего сосредоточенного
момента М его необходимо помножить на (Z-a)0 где а координата сечения, в котором приложен момент;
•в случае обрыва распределенной нагрузки ее
продлевают до конца балки, а для восстановления
действительных условий нагружения вводят
«компенсирующую» нагрузку обратного направления

39. Уравнение упругой линии балки

Метод начальных параметров
d
M ( z)
2
EI x
d z
2
Для углов поворота:
2
2
3
M pi z d i 1 M i z ai
Ri z d i
Fi z bi
qi z ci
0
2 EI x
EI x
EI x
1
2
6
Для прогибов:
3
2
3
4
M pi z d i
Ri z d i
Fi z bi
qi z ci
1 M i z ai
w w0 0 z
6 EI x
2 EI x
EI x
2
6
24
2
Где — угол поворота сечения, w — прогиб, 0 — угол поворота в начале
координат, w0 — прогиб в начале координат, di — расстояние от начало
координат до i-той опоры балки, ai — расстояние от начало координат до
точки приложения сосредоточенного момента Mi , bi — расстояние от
начало координат до точки приложения сосредоточенной силы Fi , сi —
расстояние от начало координат до начала участка распределенной
нагрузки qi , Ri и Мрi — реакция и реактивный момент в опорах балки.

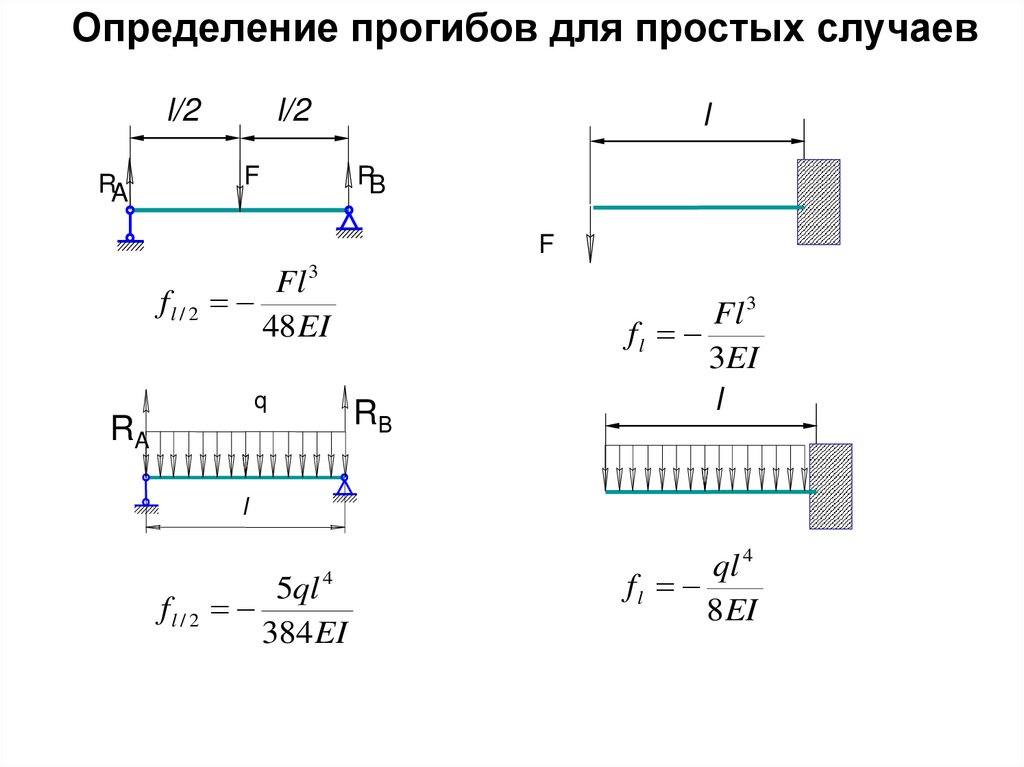
40. Определение прогибов для простых случаев

l/2
RA
l/2
F
l
RB
F
Fl 3
fl / 2
48 EI
q
RA
RВ
Fl 3
fl
3EI
l
l
5ql 4
fl / 2
384 EI
ql 4
fl
8 EI

41. УДАЧИ!!!!!