Множественная регрессия

1.

Множественная регрессия

2.

Вопросы
1. Классическая модель множественной линейной регрессии
2. Оценка параметров модели по методу наименьших квадратов
3. Анализ вариации зависимой переменной. Коэффициент детерминации и
скорректированный коэффициент детерминации
4. Гипотезы
5. Проверка адекватности линейной регрессионной модели на основе
статистических тестов.
6. Проверка значимости оценок параметров модели по t-критерия Стьюдента
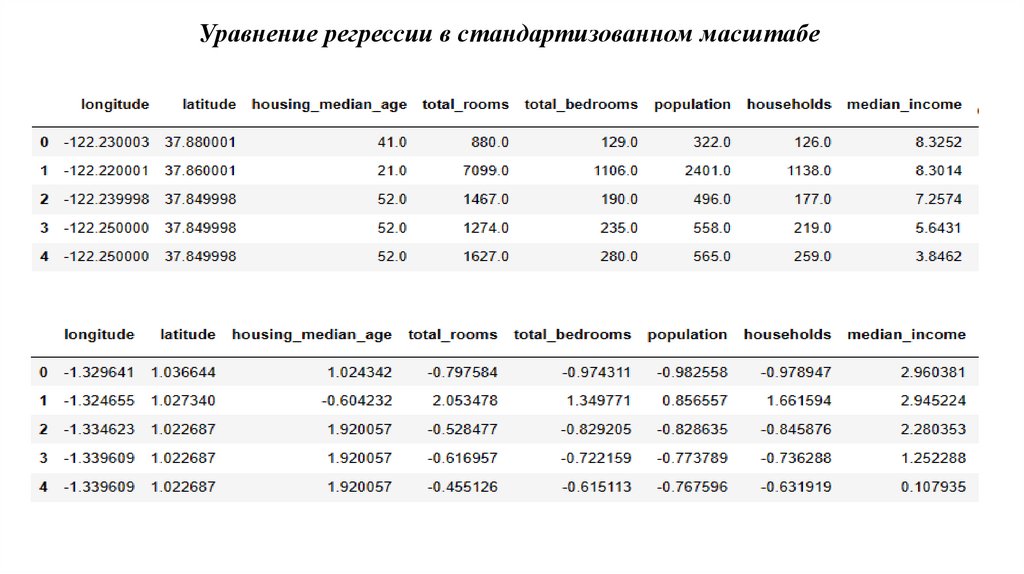
7. Уравнение регрессии в стандартизованном масштабе
8. Частные корреляции
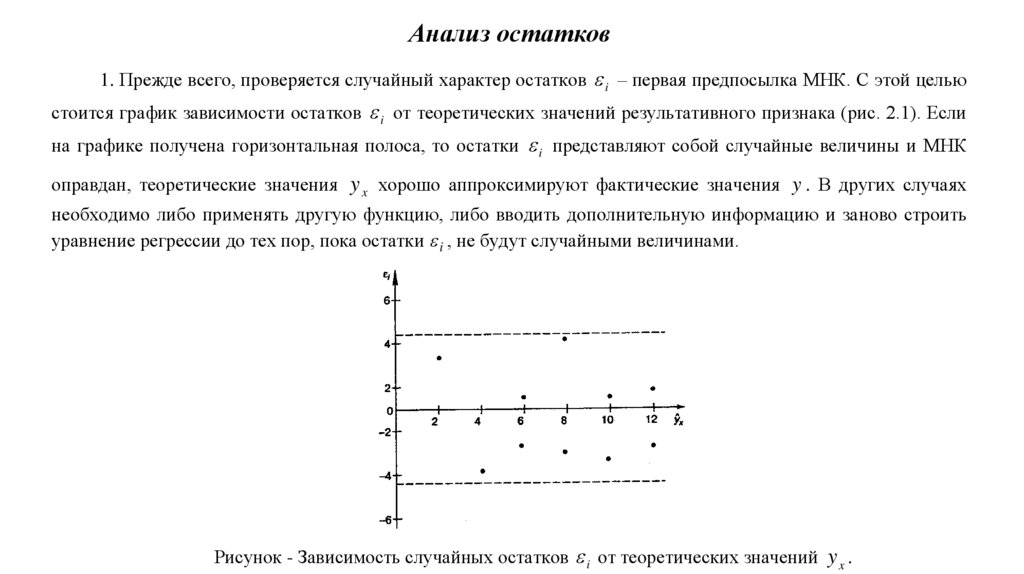
9. Анализ остатков
10. Прогнозирование в регрессионных моделях.

3.

Классическая модель множественной линейной регрессии
Естественным обобщением модели парной регрессии является модель множественной регрессии (multiple
regression model):
y f ( x1 , x 2 , , x m ) .
Модель множественной линейной регрессии имеет вид:
y 0 1 x1 2 x 2 m x m
(1)
yi 0 1 xi1 2 xi 2 m xim i ,
(2)
или для отдельного i -го наблюдения:
где x ik – значение регрессора x k в i -м наблюдении, i 1, n , k 1, m . Далее будем рассматривать модели
множественной линейной регрессии.
Предпосылки, лежащие в основе модели множественной линейной регрессии, являются естественным обобщением
соответсвующих предпосылок модели парной регрессии.

4.

Классическая модель множественной линейной регрессии
Предпосылка 1. Модель является линейной относительно параметров. Спецификация модели имеет вид
(2).
Предпосылка 2.1. В модели переменная i есть случайная величина, а объясняющие переменные xi1 , xi 2 , , xim
– детерминированные величины, то есть предполагается, что они измерены без ошибок, i 1, n .
Предпосылка 2.2. Векторы xk ( x1k , x2k , , xnk ) , k 1, m , – линейно независимы в R n . Данное условие означает
отсутствие мультиколлинеарности.
Предпосылка 3. Математическое ожидание случайного члена i в любом наблюдении равно нулю:
M ( i ) 0 , i 1, n .
Случайные ошибки в среднем не оказывают влияния на зависимую переменную.

5.

Классическая модель множественной линейной регрессии
Предпосылка 4. Гомоскедастичность – дисперсия случайного члена i постоянна для всех наблюдений:
D( i ) D( j ) 2 , i, j 1, n .
Предпосылка 5.
Отсутствие автокорреляции – случайные составляющие i и
j
являются
некоррелированными:
0, i j,
cov( i , j ) M ( i j ) 2
, i j.
Предпосылка 6. Случайные составляющие i имеют нормальное распределение:
i N (0; 2 ) , i 1, n .
При выполнении перечисленных предпосылок модель называется нормальной линейной регрессионной
моделью.

6.

Классическая модель множественной линейной регрессии
Гипотезы, лежащие в основе множественной регрессии, удобно записать в матричной форме, которая
облегчает расчетные процедуры и главным образом будет использоваться в дальнейшем.
Пусть:
- Y ( y1 , y 2 , , y n ) – вектор-столбец наблюдений зависимой переменной;
- ( 0 , 1 , , m ) – вектор-столбец параметров (неизвестных коэффициентов, подлежащих оцениванию по
выборке);
-
( 1 , 2 , , n ) – вектор-столбец случайных составляющих (случайный член);
-
1
1
X
1
x11
x 21
x n1
x1m
x2m
– матрица значений объясняющих переменных, которая называется информационной
x nm
матрицей или матрицей плана эксперимента. Столбцами матрицы
x k ( x1k , x 2 k , , x nk ) – вектор наблюдений регрессора x k , k 1, m .
X
являются векторы регрессоров:

7.

Классическая модель множественной линейной регрессии
-
1
1
X
1
x11
x 21
x n1
x1m
x2m
– матрица значений объясняющих переменных, которая называется информационной
x nm
матрицей или матрицей плана эксперимента. Столбцами матрицы X являются векторы регрессоров:
x k ( x1k , x 2 k , , x nk ) – вектор наблюдений регрессора x k , k 1, m .
Следует обратить внимание, что в матрицу X дополнительно введен столбец, все элементы которого равны
1, то есть условно полагается, что в модели (2) свободный член 0 умножается на фиктивную переменную
x0 (1, 1, , 1) , принимающую значение 1 для всех наблюдений. Добавление в модель такой компоненты, как
вектор случайных составляющих, необходимо в связи с практической невозможностью оценить связь между
переменными со стопроцентной точностью.
В матричной форме линейная модель допускает представление в виде:
Y X .

8.

Классическая модель множественной линейной регрессии
Предпосылки 1–6 в матричной записи выглядят следующим образом:
Предпосылка 1. Спецификация модели имеет вид Y X .
Предпосылка 2. Вектор – случайный вектор; матрица X – детерминированная матрица, которая имеет
максимальный ранг, равный m 1 , то есть столбцы матрицы плана X линейно независимы.
Предпосылка 3. Математическое ожидание вектора случайных составляющих равно нулю:
M 0 ,
где 0 0 n 1 – вектор-столбец из нулей.
Предпосылки 4–5. Гомоскедастичность и отсутствие автокорреляции вектора случайных составляющих:
V M T 2 En ,
где E n – n n единичная матрица.
Предпосылка 6. Случайный член подчиняется n -мерному нормальному закону распределения с нулевым
средним значением и ковариационной матрицей 2 E n :
N n 0; 2 En .

9.

Оценка параметров модели по методу наименьших квадратов
Решая систему относительно ̂ , получим явный вид оценок параметров :
ˆ ( X X ) 1 X Y .
(3)
При получении (3) мы воспользовались предположением о невырожденности матрицы X X , то есть
det( X X ) 0 или rank( X X ) m 1 , что еще раз подчеркивает необходимость выполнения предпосылки 2.2 об
отсутствии мультиколлинеарности.
Формула (3) – это формула расчета оценок ̂ параметров множественной линейной регрессии по МНК.

10.

Анализ вариации зависимой переменной. Коэффициент детерминации и
скорректированный коэффициент детерминации
Определим полную сумму квадратов (total sum of squares) отклонений yt от выборочного среднего
значения y :
n
SST ( yi y ) 2
i 1
.
Полную сумму квадратов можно представить как
SST SSR SSE ,
n
где SSR ( yˆi y ) 2 – сумма квадратов, обусловленная включенными в модель объясняющими
i 1
переменными (regression sum of squares),
n
SSE ( yi yˆi )2 – сумма квадратов остатков (error sum of squares), y – выборочное среднее наблюдений
i 1
переменной yt .
Это представление справедливо только в случае, если уравнение множественной линейной регрессии
содержит свободный член 0 .
Коэффициент детерминации, – это величина, определяемая по формуле
ESS RSS
R2 1
.
TSS TSS

11.

Анализ вариации зависимой переменной. Коэффициент детерминации и
скорректированный коэффициент детерминации
Он характеризует качество подгонки регрессионной модели к наблюдаемым значениям y i . Отметим, что
коэффициент R 2 корректно определен только в том случае, если свободный член (константа) включен в
уравнение регрессии.
Коэффициент детерминации указывает на долю вариации зависимой переменной, объясняемую
включенными в модель факторами. Он принимает значения между 0 и 1. Если R 2 0 , то это означает, что модель
не улучшает качество предсказания yt по сравнению с тривиальным yˆ t y . Если R2 1, то это означает точную
подгонку уравнения, т.е. все et 0 . Однако на R 2 нельзя ориентироваться как на главный критерий при
сравнении двух различных структур модели. Коэффициент детерминации целесообразно использовать только
совместно с дополнительным анализом регрессионного уравнения.
При сравнении качества двух регрессий на основе статистики R 2 следует помнить:
1. R 2 возрастает при увеличении числа факторных переменных.
2. R 2 изменяется даже при простейшем преобразовании зависимой переменной. Поэтому сравнивать по
значению R 2 можно только регрессии с одинаковыми зависимыми переменными.
3. Если взять число факторов, равное числу наблюдений, то можно добиться R 2 1 , но это вовсе не будет
означать наличие содержательной зависимости y от факторов.
4. R 2 зависит от крутизны поверхности регрессии. В одномерном случае при увеличении угла наклона
прямой регрессии к оси абсцисс величина R 2 может быть близка к единице при плохом качестве прогноза по
уравнению регрессии.

12.

Анализ вариации зависимой переменной. Коэффициент детерминации и
скорректированный коэффициент детерминации
Для того чтобы не допустить возможного преувеличения на основе R 2 тесноты связи y с факторными
переменными, при возрастании их числа используют скорректированный (adjusted) коэффициент
детерминации, который содержит поправку на число факторов:
2
Rкор
1
ESS /( n m 1)
.
TSS /( n 1)
Свойства скорректированного коэффициента детерминации
2
1. Rкор
1 (1 R 2 )
n 1
.
n m 1
2
2. R 2 Rкор
, m 1.
2
3. С ростом числа факторов m скорректированный коэффициент Rкор
растет медленнее, чем коэффициент
R2 .
2
4. Чем больше m , тем больше различие между R 2 и Rкор
.

13.

Анализ вариации зависимой переменной. Коэффициент детерминации и
скорректированный коэффициент детерминации
При сравнении альтернативных регрессионных моделей, отличающихся количеством объясняющих
переменных, предпочтительнее использовать скорректированный (нормированный) коэффициент детерминации. Он
позволяет учесть при оценке качества модели соотношение количества наблюдений и количества оцениваемых
параметров модели.
Скорректированный коэффициент детерминации применяется для решения двух типов задач:
– оценка тесноты связи между объясняемой и объясняющей переменной. Необходимо обратить внимание
на близость к нескорректированному коэффициенту детерминации. Модель считается качественной, если
показатели велики и несильно отличаются друг от друга.
– сравнение моделей с различным числом параметров. При прочих равных условиях, предпочтение
отдается той модели, у которой скорректированный коэффициент детерминации больше.
Следует отметить, что скорректированный коэффициент детерминации нельзя использовать в формулах,
где применяется обычный коэффициент детерминации, поскольку скорректированный коэффициент
детерминации нельзя интерпретировать как долю вариации объясняемой переменной, обусловленную вариацией
факторов, включенных в модель.
Замечание. Не следует абсолютизировать значимость коэффициента детерминации. Существует
достаточно примеров неправильно специфицированных моделей, имеющих высокий коэффициент
детерминации.

14.

Разложение коэффициента множественной детерминации на коэффициенты
отдельной детерминации
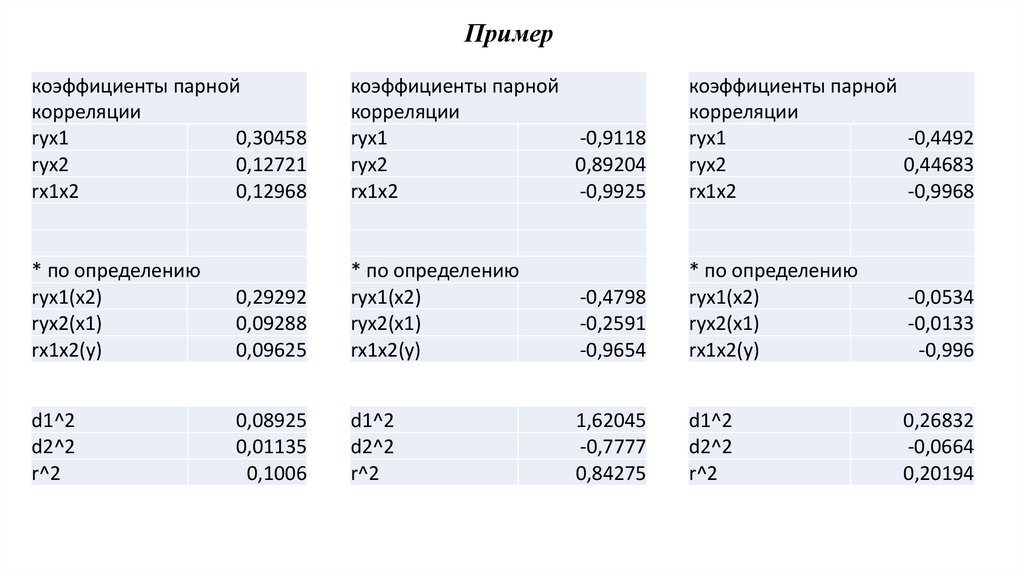
Для выяснения доли влияния каждого фактора на показатель используются коэффициенты отдельной
детерминации.
2
Коэффициентом отдельной детерминации d j для фактора X j называется произведение коэффициента
корреляции rx
j
*
между
фактором
и
показателем
и
стандартизированного
параметра
регрессии.
X
a
Y
y
j
j.
d 2j ryx j a*j
где a*j
aˆ j x j
y
,
– стандартизированный параметр регрессии.
Сумма коэффициентов отдельной детерминации равен коэффициенту множественной детерминации, то
есть
m
R норм d 2j
2
j 1
.

15.

Проверка значимости уравнения регрессии
Для проверки значимости уравнения регрессии используют F -критерий. Нулевая гипотеза состоит в том,
что коэффициенты при всех регрессорах равны нулю, то есть проверяется гипотеза
H 0 : 1 0, 2 0, ..., m 0 .
Следовательно, F -статистика, определяемая по формуле, имеет распределение Фишера:
R2 n m 1
F
2
1 R
m
RSS n m 1
RSS / m
ESS
m
ESS / (n m 1)
(Yˆ y )Τ (Yˆ y ) 1
2
σ
m F (m; n m 1),
Τ
e e
1
σ2 n m 1
(4)
и ее можно использовать для проверки гипотезы. Гипотеза H 0 отвергается, например, при уровне
значимости , если F F ( ; m; n m 1) , где F ( ; m; n m 1) – % -я точка распределения Фишера F (m; n m 1)

16.

Проверка значимости уравнения регрессии
Замечание. Число степеней свободы остаточной суммы квадратов ESS равно разности между числом
наблюдений и числом линейных связей между ними, участвующими в определении ESS ( yi yˆi )2 , то есть
n (m 1) n m 1 (для определения ŷ i требуется решить систему m 1 линейных уравнений для определения
_
оценок ˆ 0 , ˆ 1 , , ˆ m ). Для множественной регрессии сумма TSS ( yi y ) 2 имеет n 1 степеней свободы, так как в
этой сумме все наблюдения связаны одной связью (при определении значения y ). Для суммы RSS ( yˆi y )2 число
степеней свободы равно (m 1) 1 m , так как в выражение ŷi входят m 1 оценок неизвестных параметров и одна
линейная связь, определяемая y .
Статистику (4) используют для проверки гипотезы о статистической значимости коэффициента
детерминации:
H0 : R2 0 .
Это равнозначно проверке значимости уравнения регрессии и полностью совпадает с описанной выше
проверкой.
Если уравнение регрессии незначимо, то есть все коэффициенты при регрессорах для генеральной
совокупности равны нулю, то на этом анализ уравнения регрессии заканчивается. Если же нулевая гипотеза
H 0 : 1 0, 2 0, ..., m 0
отвергается, то представляют интерес проверка значимости отдельных коэффициентов регрессии и
построение интервальных оценок для значимых коэффициентов.

17.

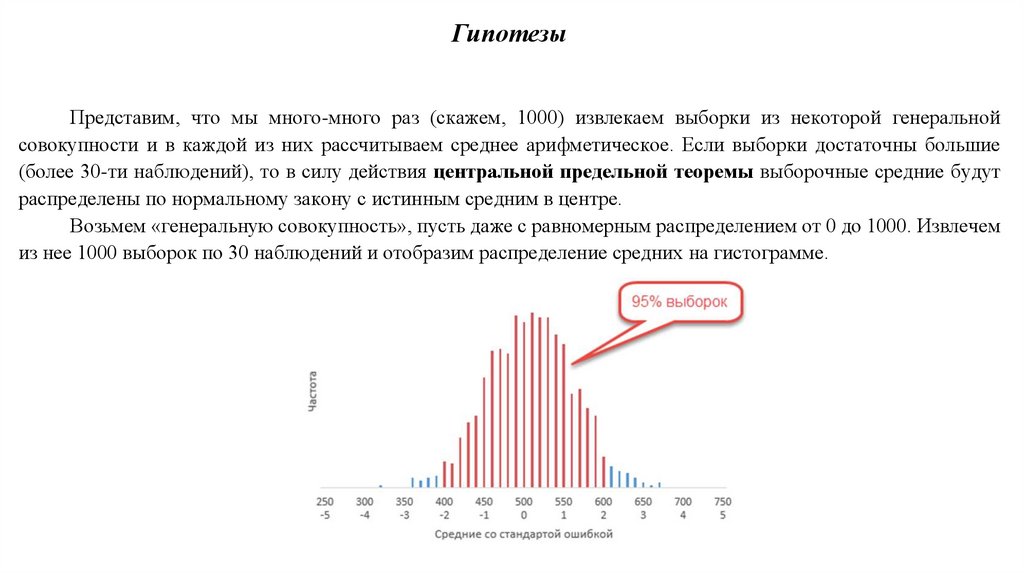
Гипотезы
Представим, что мы много-много раз (скажем, 1000) извлекаем выборки из некоторой генеральной
совокупности и в каждой из них рассчитываем среднее арифметическое. Если выборки достаточны большие
(более 30-ти наблюдений), то в силу действия центральной предельной теоремы выборочные средние будут
распределены по нормальному закону с истинным средним в центре.
Возьмем «генеральную совокупность», пусть даже с равномерным распределением от 0 до 1000. Извлечем
из нее 1000 выборок по 30 наблюдений и отобразим распределение средних на гистограмме.

18.

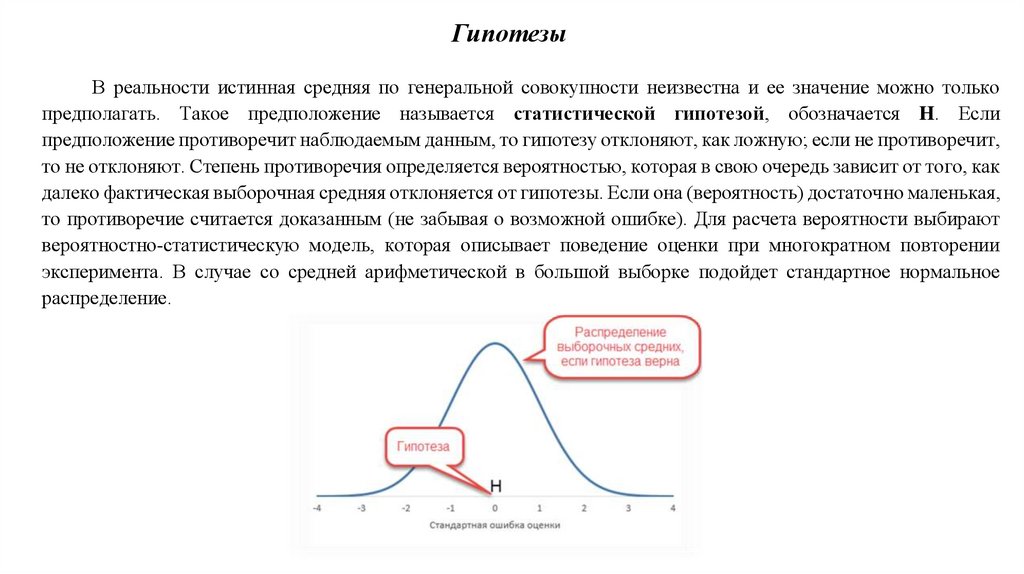
Гипотезы
В реальности истинная средняя по генеральной совокупности неизвестна и ее значение можно только
предполагать. Такое предположение называется статистической гипотезой, обозначается H. Если
предположение противоречит наблюдаемым данным, то гипотезу отклоняют, как ложную; если не противоречит,
то не отклоняют. Степень противоречия определяется вероятностью, которая в свою очередь зависит от того, как
далеко фактическая выборочная средняя отклоняется от гипотезы. Если она (вероятность) достаточно маленькая,
то противоречие считается доказанным (не забывая о возможной ошибке). Для расчета вероятности выбирают
вероятностно-статистическую модель, которая описывает поведение оценки при многократном повторении
эксперимента. В случае со средней арифметической в большой выборке подойдет стандартное нормальное
распределение.

19.

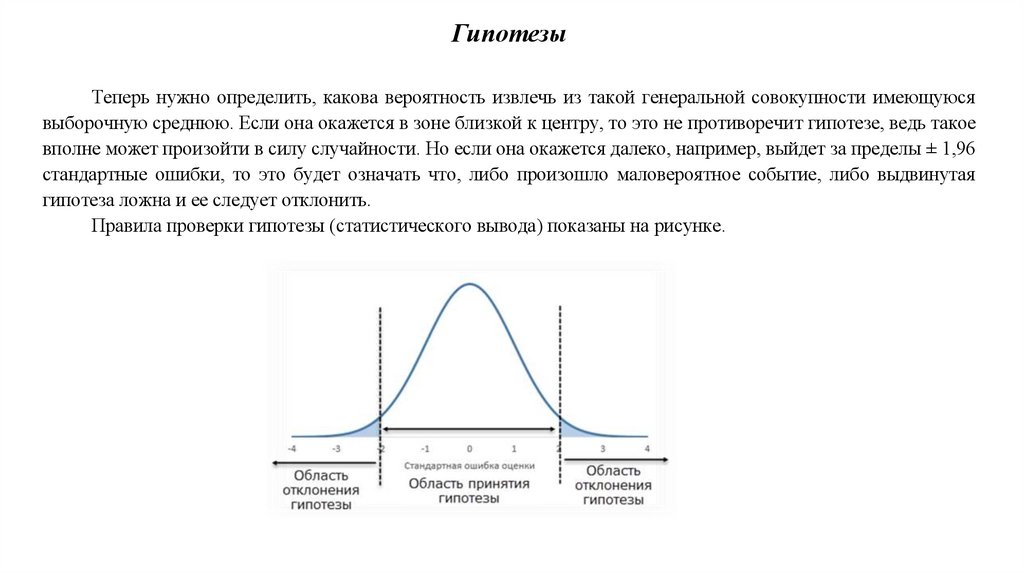
Гипотезы
Теперь нужно определить, какова вероятность извлечь из такой генеральной совокупности имеющуюся
выборочную среднюю. Если она окажется в зоне близкой к центру, то это не противоречит гипотезе, ведь такое
вполне может произойти в силу случайности. Но если она окажется далеко, например, выйдет за пределы ± 1,96
стандартные ошибки, то это будет означать что, либо произошло маловероятное событие, либо выдвинутая
гипотеза ложна и ее следует отклонить.
Правила проверки гипотезы (статистического вывода) показаны на рисунке.

20.

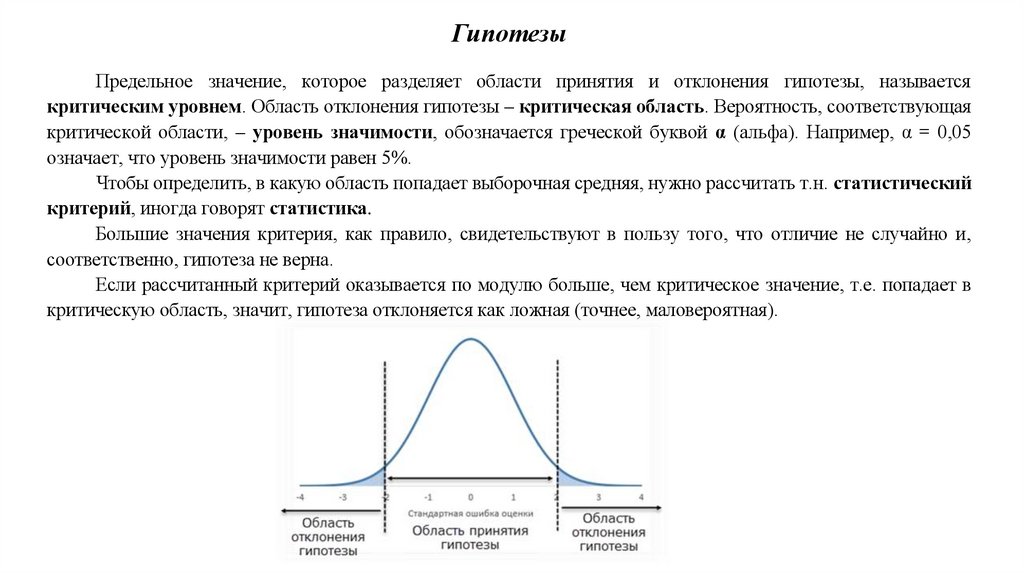
Гипотезы
Предельное значение, которое разделяет области принятия и отклонения гипотезы, называется
критическим уровнем. Область отклонения гипотезы – критическая область. Вероятность, соответствующая
критической области, – уровень значимости, обозначается греческой буквой α (альфа). Например, α = 0,05
означает, что уровень значимости равен 5%.
Чтобы определить, в какую область попадает выборочная средняя, нужно рассчитать т.н. статистический
критерий, иногда говорят статистика.
Большие значения критерия, как правило, свидетельствуют в пользу того, что отличие не случайно и,
соответственно, гипотеза не верна.
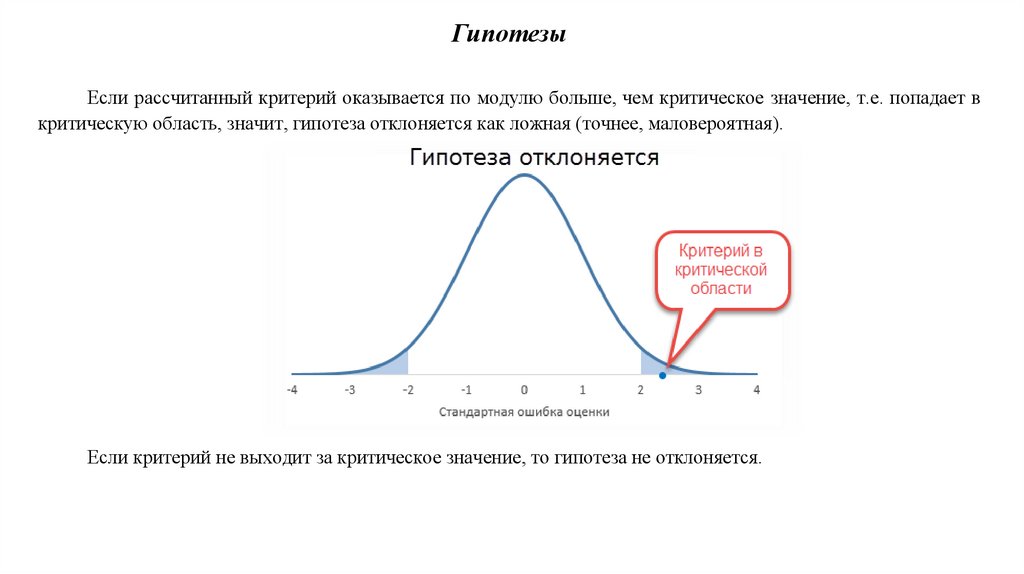
Если рассчитанный критерий оказывается по модулю больше, чем критическое значение, т.е. попадает в
критическую область, значит, гипотеза отклоняется как ложная (точнее, маловероятная).

21.

Гипотезы
Если рассчитанный критерий оказывается по модулю больше, чем критическое значение, т.е. попадает в
критическую область, значит, гипотеза отклоняется как ложная (точнее, маловероятная).
Если критерий не выходит за критическое значение, то гипотеза не отклоняется.

22.

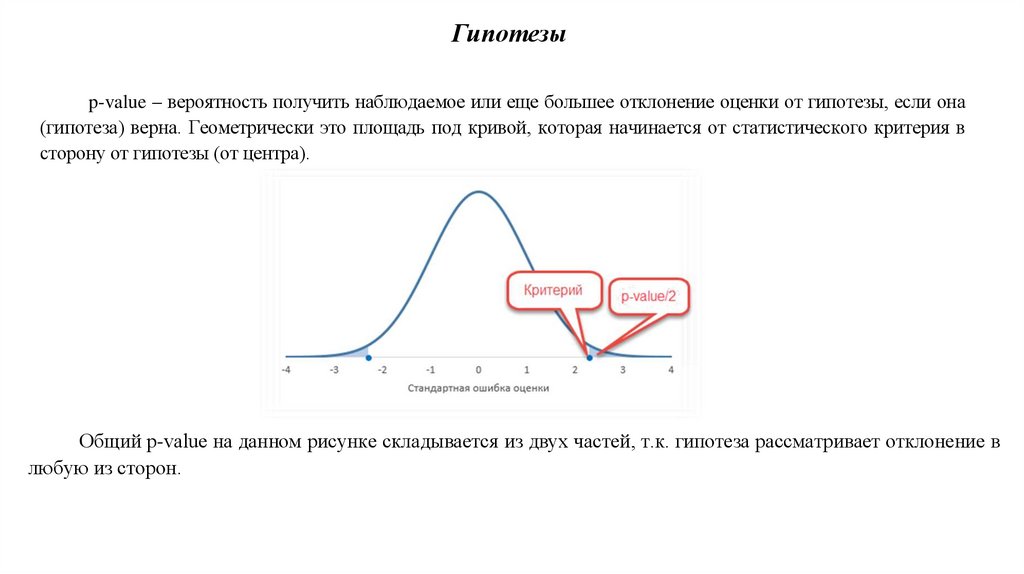
Гипотезы
p-value – вероятность получить наблюдаемое или еще большее отклонение оценки от гипотезы, если она
(гипотеза) верна. Геометрически это площадь под кривой, которая начинается от статистического критерия в
сторону от гипотезы (от центра).
Общий p-value на данном рисунке складывается из двух частей, т.к. гипотеза рассматривает отклонение в
любую из сторон.

23.

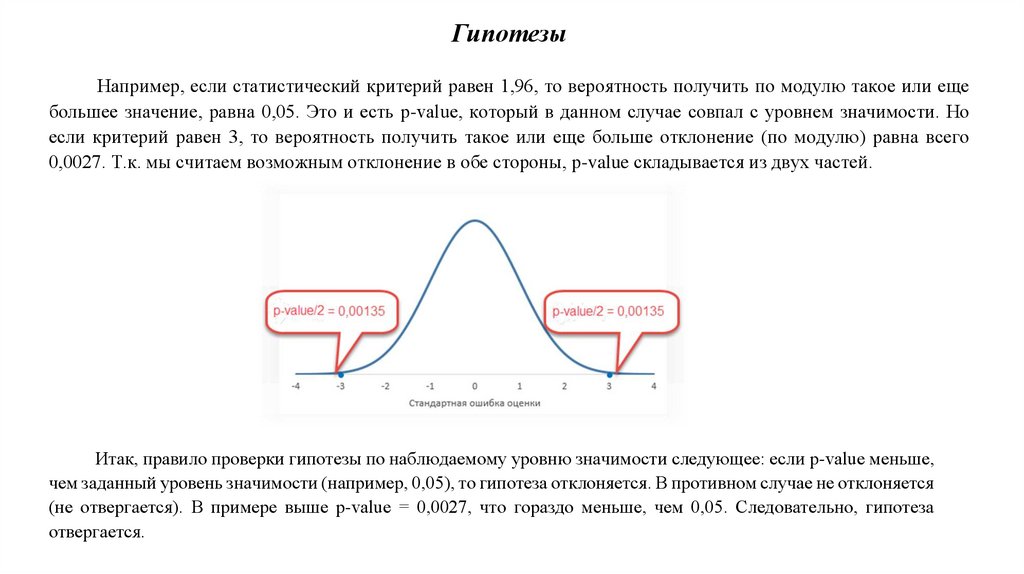
Гипотезы
Например, если статистический критерий равен 1,96, то вероятность получить по модулю такое или еще
большее значение, равна 0,05. Это и есть p-value, который в данном случае совпал с уровнем значимости. Но
если критерий равен 3, то вероятность получить такое или еще больше отклонение (по модулю) равна всего
0,0027. Т.к. мы считаем возможным отклонение в обе стороны, p-value складывается из двух частей.
Итак, правило проверки гипотезы по наблюдаемому уровню значимости следующее: если p-value меньше,
чем заданный уровень значимости (например, 0,05), то гипотеза отклоняется. В противном случае не отклоняется
(не отвергается). В примере выше p-value = 0,0027, что гораздо меньше, чем 0,05. Следовательно, гипотеза
отвергается.

24.

Гипотезы
Проверяемая гипотеза называется основной или нулевой. Она подразумевает некоторый status quo, когда
между проверяемыми данными нет отличий. Гипотеза остается в силе, если оценка отклонятся не слишком
далеко и находится в зоне возможных случайных колебаний.
Кроме основной (нулевой) гипотезы рассматривают альтернативную или конкурирующую. Формально,
альтернативная гипотеза – это любое предположение о параметрах распределения, не совместимое с нулевой
гипотезой. Однако на практике разнообразие проверяемых и альтернативных гипотез довольно ограничено.
Например, основная гипотеза (нулевая) заключается в том, что средняя равна некоторому значению, а
альтернативная – не равна этому значению.
Нулевая гипотеза обозначается H0, альтернативная Ha. Краткая запись условия задачи при использовании
двухстороннего критерия имеет следующий вид.
H0: μ = a
Ha: μ ≠ a
Если рассматривается односторонний критерий, то запись может иметь такой вид.
H0: μ ≤ a
Ha: μ > a
При отклонении нулевой гипотезы, автоматически принимается альтернативная.

25.

Гипотезы
Следует отметить, что предметом доказательства, как правило, является именно конкурирующая гипотеза.
То есть проверяя равенство средних в двух выборках, исследователя интересует их различие, которое должно
подтвердить влияние некоторого воздействия на предмет исследования (новое лекарство, новых способ
обработки материала и др.). Если есть влияние, то будет и различие, если нет, то средние будут отличаться не
очень сильно, в пределах случайных колебаний оценок.
Заострим внимание на корректности статистических выводов. Вместо выражения «гипотеза не
отклоняется» часто говорят «гипотеза принимается». В целом, это выражение также приемлемо, если его
понимать правильно, т.е. если считать, что принимается именно гипотеза (одно из возможных объяснений), а не
конкретное утверждение. Но понимают его часто неправильно, подразумевая, что в случае не отклонения
гипотезы принимается сама идея гипотезы. Например, если гипотеза о равенстве вероятностей в двух выборках
не отклоняется, то делают заключение, что, мол, вероятности действительно равны. Такое заключение ошибочно.
На самом деле принятие гипотезы означает, что она не противоречит данным и может рассматриваться до
тех пор, пока не будет доказано обратное. Принятие гипотезы не может доказать ее правильность, для этого есть
лишь один способ: исследовать все анализируемое явление в целом, собрав генеральную совокупность. По
выборке можно только опровергнуть маловероятные или невозможные предположения, противоречащие
фактическим данным, сузив тем самым круг для поиска истины.

26.

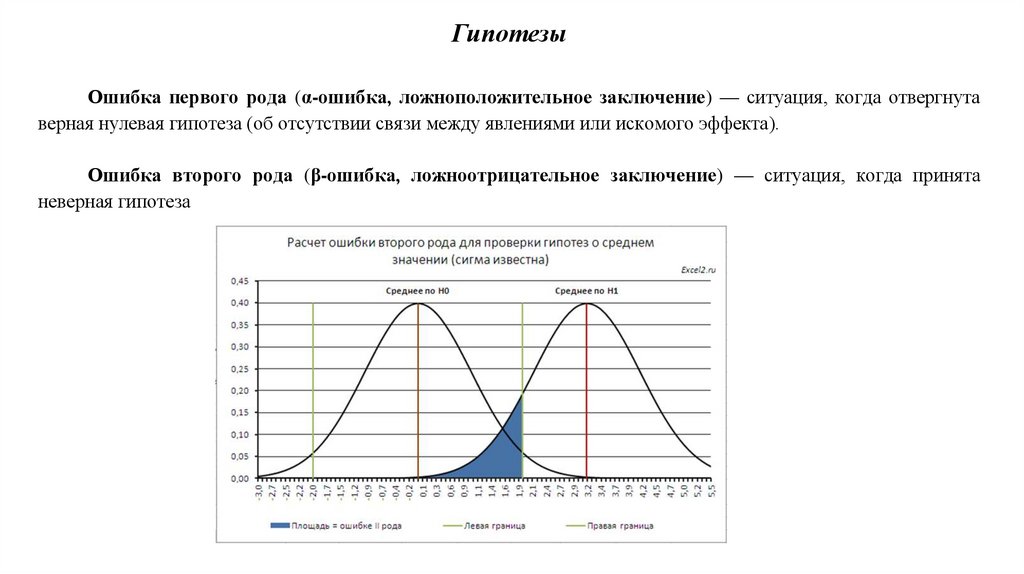
Гипотезы
Ошибка первого рода (α-ошибка, ложноположительное заключение) — ситуация, когда отвергнута
верная нулевая гипотеза (об отсутствии связи между явлениями или искомого эффекта).
Ошибка второго рода (β-ошибка, ложноотрицательное заключение) — ситуация, когда принята
неверная гипотеза

27.

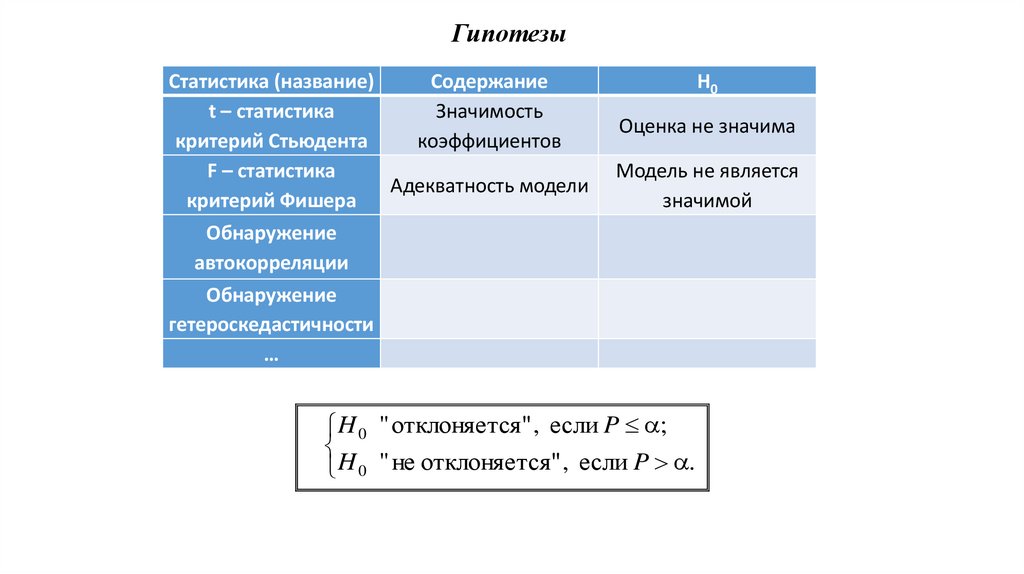
Гипотезы
Статистика (название)
Содержание
t – статистика
Значимость
критерий Стьюдента
коэффициентов
F – статистика
Адекватность модели
критерий Фишера
Н0
Оценка не значима
Модель не является
значимой
Обнаружение
автокорреляции
Обнаружение
гетероскедастичности
…
H 0 " отклоняется" , если P ;
H 0 " не отклоняется" , если P .

28.

Проверка адекватности линейной регрессионной модели на основе
статистических тестов.
Алгоритм тестирования по F-критерию Фишера
Шаг 1. Формулировка нулевой и альтернативной гипотез
Н0: aˆ0 aˆ1 aˆm 0 , то есть ни один фактор модели не влияет на показатель, или все параметры модели
незначимы.
НА: хотя бы одно значение â j отличное от нуля, то есть aˆ j 0, j 0; m .
Шаг 2. Выбор подходящего уровня значимости
Уровнем значимости называется вероятность сделать ошибку 1-го рода, то есть отклонить правильную
гипотезу. Величина P 1 называется уровнем доверия или доверительной вероятностью.
В электронных таблицах Ехсеl по умолчанию принимается 0,05 ( P 0,95) . Это означает, что мы рискуем
отклонить правильную гипотезу в 5% случаев, а в 95% случаев наши выводы будут верными.
Шаг 3. Расчет расчетного значения F-критерия
Расчетное значение F-критерия, так называемое F-отношение, определяется по формуле:
F расч
R2
1 R
2
n m 1
,
m
где R 2 – коэффициент множественной детерминации.
Примечание. При использовании электронных таблиц Ехсеl расчетное значение F-критерия можно найти

29.

n m 1
F
,
Проверка адекватности линейной
регрессионной
модели на основе
расч
2
m
1 R
R2
статистических тестов.
где R 2 – коэффициент множественной детерминации.
Примечание. При использовании электронных таблиц Ехсеl расчетное значение F-критерия можно найти
в таблице Дисперсионный анализ вывода итогов пакета Анализ данных - регрессии.
Шаг 4. Определение по статистическим таблицам F-распределения Фишера критического значения
F-критерия
Критическое значение F-критерия находят по статистическим таблицам F-распределения Фишера за
соответствующими значениями:
– доверительной вероятности Р;
– степеней свободы k1 m и k 2 n m 1 .
Шаг 5. Сравнение расчетного значения F-критерия с критическим и интерпретация результатов
тестирования
Если F расч Fкр , то нет оснований отклонить нулевую гипотезу о том, что ни один фактор модели не
является значимым, то есть с принятой надежностью можно утверждать, что модель неадекватна;
Если F расч Fкр , то нулевая гипотеза о незначительности факторов отклоняется есть с принятой
надежностью можно утверждать, что модель адекватна.

30.

Проверка значимости оценок параметров модели по t-критерия Стьюдента
Алгоритм тестирования по t-критерию Стьюдента
Шаг 1. Формулировка нулевой и альтернативной гипотез
H 0 : aˆ 0 0, j 0; 2 , – оценка j-го параметра является статистически незначимой, и j-й фактор никак не
влияет на показатель y;
H 1 : aˆ 0 0, j 0; 2 – оценка j-го параметра является статистически значимой, и j-й фактор никак влияет
на показатель y.
Шаг 2. Выбор подходящего уровня значимости
Уровень значимости избирается аналогично F-критерия.
Шаг 3. Расчет расчетного значения t-критерия
Расчетные значения t-критерия определяются по формулам:
aˆ
ˆtaˆ j , j 0; m
j
ˆ aˆ j
.
При анализе двухфакторной модели расчетные значения t-критерия определяются по формулам:
aˆ
aˆ
aˆ
tˆaˆ 0 0 ,
tˆaˆ1 1 ,
tˆaˆ 2 2
ˆ aˆ 0
ˆ aˆ1
ˆ aˆ 2
.

31.

Проверка значимости оценок параметров модели по t-критерия Стьюдента
Шаг 4. Определение по статистическим таблицам t-распределения Стьюдента критического
значения t-критерия
Критическое значение t-критерия находят по статистическим таблицам t-распределения Стьюдента по
соответствующим значениями:
– доверительной вероятности Р;
– числом степеней свободы k n m 1 .
Шаг 5. Сравнение расчетного значения t-критерия с критическим и интерпретация результатов
тестирования
Если