Средства измерений и обработка результатов измерений

1.

Тема: Средства измерений и
обработка результатов измерений
С.В. Муравьев
e-mail: [email protected]
Томский политехнический университет
1

2.

12
Лекция
Прямые многократные измерения
Порядок обработки прямых многократных измерений
Проверка нормальности распределения результатов наблюдения
Введение поправок в результаты измерений
Косвенные измерения
Порядок обработки косвенных измерений
Упрощенный расчет погрешности косвенных измерений
Учет погрешности констант
2

3.

Исходные предположения
Прямыми называются измерения, в результате которых искомое значение
физической величины находят непосредственно из опытных данных.
Пусть прямые измерения осуществляются путем многократных наблюдений.
Результаты таких наблюдений x1, x2, …, xn называются
равнорассеянными (равноточными или гетероскедастичными), если они
являются независимыми, одинаково распределенными случайными величинами,
т.е. 1 = 2 = … = n = ;
и получаются при измерениях, проводимых
одним наблюдателем или группой наблюдателей
с помощью одних и тех же методов и средств измерений
в неизменных условиях внешней среды.
При этом
1) обрабатывается ограниченная группа из n наблюдений;
2) результаты наблюдений хi могут содержать систематическую погрешность;
3) в группе наблюдений могут встречаться грубые погрешности;
4) распределение случайных погрешностей может отличаться от нормального.
3

4.

Порядок
обработки
прямых многократных
измерений
4

5.

Обработка результатов наблюдений в соответствии с
ГОСТ 8.736-2011 ГСИ. Измерения прямые многократные. Методы обработки
результатов измерений. Основные положения
(Старая версия: ГОСТ 8.207-76 ГСИ. Прямые измерения с многократными
наблюдениями. Методы обработки результатов наблюдений. Основные
положения)
производится в следующем порядке.
1. Путем введения поправок из результатов наблюдений исключают известные
систематические погрешности:
погрешности метода,
погрешности средств измерений (например, выражаемые пределами
допускаемых основной и дополнительных погрешностей, если их случайные
составляющие пренебрежимо малы)
и др.
2. Вычисляют среднее арифметическое
1 n
x xi
n i 1
исправленных результатов наблюдений, принимая его за оценку истинного
значения измеряемой величины.
5

6.

3. Вычисляют оценку
1 n
2
S
(
x
x
)
i
n 1 i 1
среднеквадратического отклонения результатов наблюдений и оценку
S
S(x ) S x
n
среднеквадратического отклонения среднего арифметического (результата
измерения).
4. Проверяют гипотезу о нормальности распределения результатов
наблюдения.
При n < 15 нормальность распределения не проверяется.
Если 15 < n < 50 – используют составной критерий.
Если число результатов n > 50, используют критерий Пирсона 2 или
критерий Мизеса-Смирнова 2.
Уровень значимости выбирается из интервала 0,02 – 0,10.
6

7.

Составной критерий
Распределение результатов наблюдения считается отличным от нормального, если оно не
соответствует хотя бы одному из двух критериев.
Критерии
Гипотеза о нормальности
принимается, если
Первый:
d 1 0.5q1 d d 0.5q1 ,
n
d
| xi x |
i 1
n
1
( xi x ) 2
n i 1
распределения
где q1 – выбранный уровень значимости;
d 1 0.5q1 и d 0.5q1 – квантили, выбираемые из
таблицы
квантилей
распределения
статистики d.
Второй: квантиль z 0.5P интегральной не более m разностей | x i x | превосходят
функции нормированного нормального уровень
z 0.5 Pд / S ,
распределения,
отвечающий
вероятности P/2 (см. таблицу функции где S – оценка СКО результатов наблюдения,
Лапласа)
параметр m берется из таблицы и равен 1 или 2.
7

8.

5. Если результаты наблюдений распределены нормально, то определяют
наличие грубых погрешностей и промахов и если последние обнаружены,
соответствующие результаты отбраковывают и повторяют вычисления.
6. Вычисляют доверительные границы случайной погрешности при
доверительной вероятности P = 0,95, (а также при P = 0,99, если измерения в
дальнейшем повторить нельзя).
Доверительные границы определяют по формуле:
t S(x ) ,
где t – коэффициент Стьюдента для данного уровня доверительной вероятности
Р и объема выборки n.
Число степеней свободы принимается равным n – 1.
8

9.

7. Определяют границы неисключенной систематической погрешности
(НСП) результата измерений.
В качестве составляющих НСП рассматривают те, поправки на которые не были
введены, поскольку их значения неизвестны. К ним могут относиться:
погрешности определения поправок;
погрешности, зависящие от точности измерения влияющих величин,
входящих в формулы для определения поправок;
погрешности, связанные с колебаниями влияющих величин (температуры
окружающей среды, напряжения питания и т.д.).
Для того, чтобы иметь возможность систематические погрешности
комбинировать
со
случайными,
неисключенные
систематические
погрешности рассматриваются как случайные величины. Если их
распределение неизвестно, то принимается равномерное распределение.
9

10.

Границы НСП при наличии m составляющих систематической погрешности
определяют по формуле:
k 12 22 ... 2m k
m
2
i,
i 1
где i – границы каждой из m составляющих;
k – коэффициент, зависящий от доверительной вероятности и m.
Рекомендованные значения k (независисмо от m):
k = 0,95 при доверительной вероятности P = 0,9 и
k = 1,1 при P = 0,95 и
k = 1,4 при P = 0,99.
Эта формула представляет собой геометрическую сумму статистически
независимых погрешностей.
10

11.

8. Вычисляют доверительные границы погрешности результата .
На этом этапе суммируются (комбинируются) систематическая и
случайная составляющая погрешности
Если 0,8 S ( x ) , то НСП пренебрегают, и результат характеризуют
только случайной погрешностью, т.е.
.
Если 8 S ( x ) , то результат характеризуют только границами НСП,
т.е.
.
11

12.

Если 0,8S ( x ) 8S ( x ) , то ГОСТ 8.736-2011 рекомендует
погрешности результата измерений находить по формуле
tS ( x )
m
границу
S ,
1
2
S(x )
i
3 i 1
1 m 2
i S ( x ) 2 – оценка суммарного СКО суммарной погрешности;
где S
3 i 1
1 m 2
i – дисперсия НСП, для которых принято равномерное распределение,
3 i 1
S ( x ) 2 – дисперсия НСП, для которых принято нормальное распределение.
Примечание. Подход по ГОСТ 8.736-2011 приводит к заниженной оценке
границы. Можно использовать оценку, предложенную П.В. Новицким:
[| | tS ( x )]
12

13.

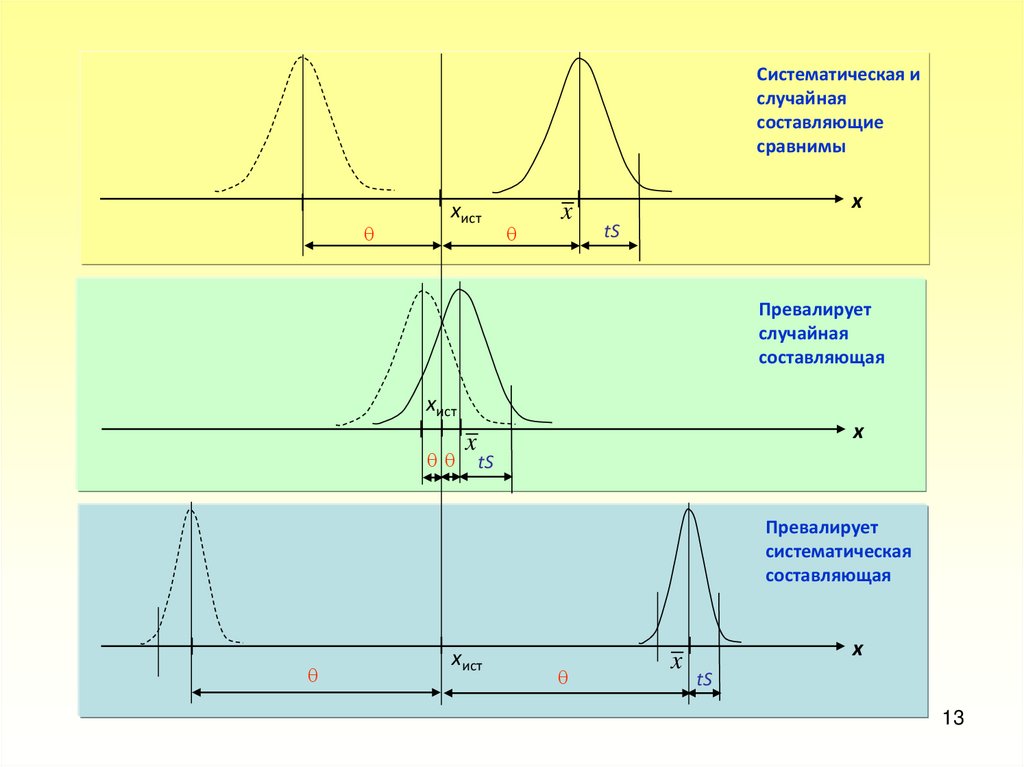
Cистематическая и
случайная
составляющие
сравнимы
xист
x
x
tS
Превалирует
случайная
составляющая
xист
x
x
tS
Превалирует
систематическая
составляющая
xист
x
x
tS
13

14.

9. Результат измерения записывают в виде
x , Pд ,
а при отсутствии сведений о виде функции распределения
составляющих погрешности и необходимости дальнейшей обработки
результатов и анализа погрешностей – в виде
x , S , n, .
14

15.

Проверка нормальности
эмпирического
распределения
результатов многократных
наблюдений по критерию
Пирсона (п. 4)
15

16.

Для идентификации форма закона распределения погрешностей
экспериментальных данных требуется построение гистограммы
эмпирического
распределения
результатов
многократных
наблюдений.
Пример: имеются 100 результатов измерений нормально распределенной
величины.
x
Так выглядят для приведенных выше данных гистограммы для m = 25 и m = 4 и
аппроксимирующая их функция плотности вероятности, где m – число
интервалов группирования.
m
m
x
x
16

17.

Чтобы построить гистограмму, необходимо выполнить следующие действия.
1. Cтроим вариационный ряд результатов многократных наблюдений xi , т.е.
располагаем их в порядке неубывания:
x(1) x(2) … x(n–1) x(n).
2. Выбираем число интервалов группирования m.
"Оптимальное" значение может
рекомендациям:
Старджес: m = 3,3 lg n + 1
Брукс и Каррузер: m = 5 lg n
Хайнхольд: m n и др.
быть
определено
по
различным
Например, для n = 20 m 5…6.
Число m удобно принимать нечетным, располагая центральный столбец
симметрично относительно принятого центра распределения
17

18.

3. Выбираем длину h интервала группирования (ширину столбца гистограммы)
Можно пользоваться формулой:
h
xmax xmin
.
m
Значение h всегда округляется в большую сторону.
Для определения координат центра столбца удобно, чтобы h делилось на 2.
Затем вариационный ряд обычно разбивается на равные интервалы:
границы первого интервала 1: [ ; xmin h / 2] ;
границы второго интервала 2: ( xmin h / 2; xmin 3h / 2] ; и т.д.
до m: ( xmin (m 2)h h / 2; ] .
4. Вычисляем относительные частоты
nk
,
n
где k = 1, …, m;
nk – число значений x из вариационного ряда, попавших в k-ый
интервал группирования;
18

19.

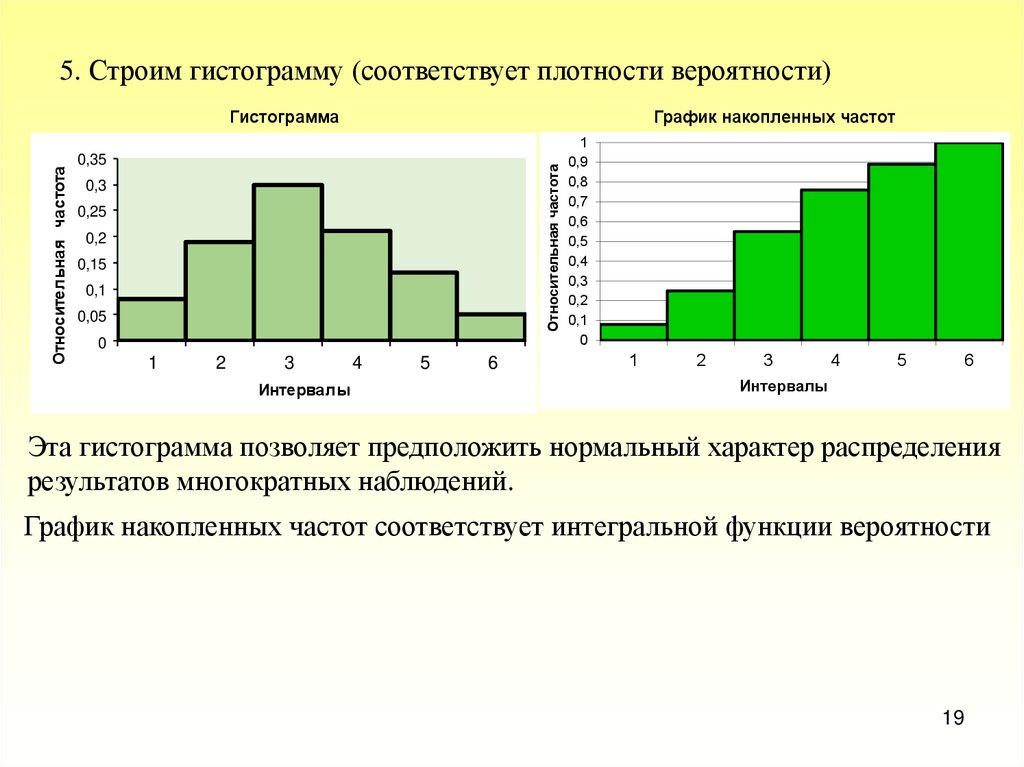
5. Строим гистограмму (соответствует плотности вероятности)
График накопленных частот
0,35
Относительная частота
Относительная частота
Гистограмма
0,3
0,25
0,2
0,15
0,1
0,05
0
1
2
3
Интервалы
4
5
6
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
1
2
3
4
5
6
Интервалы
Эта гистограмма позволяет предположить нормальный характер распределения
результатов многократных наблюдений.
График накопленных частот соответствует интегральной функции вероятности
19

20.

Проверка гипотез
Нулевая гипотеза: данные соответствуют предполагаемому закону.
Альтернативная гипотеза: данные не соответствуют предполагаемому
закону.
Процедура проверки гипотезы состоит в
вычислении некоторой функции выборочных данных, называемой
проверочной статистикой или критерием, и
выяснении, попадает ли ее значение в критическую область, которая
зависит от выбранного уровня значимости.
Нулевая гипотеза принимается, если проверочная статистика не попадает в
критическую область.
20

21.

Критерий 2 (критерий согласия Пирсона)
Основан на сравнении эмпирических площадей столбцов гистограммы с
теоретическими площадями под соответствующими участками графика
плотности распределения f(x), вычисленными в предположении о нормально
распределенной генеральной совокупности, соответствующем нулевой
гипотезе.
Эти теоретические площади можно вычислить по очевидной
формуле
Pk
xk h
xk
f ( x)dx ,
где k – номер интервала группирования, h – ширина
интервала.
Карл Пирсон (1857-1936) ,
английский математик,
статистик
21

22.

Критерий 2 вычисляется как сумма нормированных квадратов
разностей эмпирических и теоретических площадей по всем m
интервалам группирования:
m
( nk nPk ) 2
2
.
nP
k
k 1
Это случайная величина (статистика), которая имеет собственный закон
распределения
Граничные (критические) значения критерия для уровней значимости
2
2
0,1 и 0,05 (соответственно 0,9
и 0,95
) приведены в таблице.
m 1 r
2
4
2
4,60 7,78
0,9
2
0,95
5,99 9,49
6
8
10
12
14
16
10,65 13,36 15,99 18,55 21,96 23,54
12,59 15,51 18,31 21,03 23,68 26,30
Число степеней свободы для нормального закона равно m 3 , т.к. число
параметров теоретического закона r = 2.
2
Нулевая гипотеза принимается, если 2 гр
22

23.

Введение поправок
в результаты
измерений (п. 1)
23

24.

Процедура
обработки
результатов
многократных
измерений
предусматривает исключение известных систематических погрешностей
из результатов наблюдений путем введения поправок.
Введение поправок основано на знании систематической погрешности и
закономерности ее изменения.
Для исключения систематической погрешности в показания прибора
вносят поправки, равные этим погрешностям, но с обратным знаком.
При этом как источники, так и условия возникновения систематических
погрешностей неизбежно в той или иной мере изменяются.
После введения поправки случайные отклонения значений погрешности
от значений поправки останутся неисключенными. Это случайное по
характеру различие значений систематической погрешности при повторении
измерения, которое невозможно исключить, называют неисключенной
составляющей систематической погрешности (НСП).
24

25.

Значение
поправки
с
определяют
экспериментально
при
поверке/калибровке приборов или в результате специальных исследований.
Для исправления i-го результата наблюдения x i его складывают со средним
арифметическим значением c поправки:
где
x i x i c
x i – исправленный результат наблюдений,
Если c , где – систематическая погрешность, то эта погрешность
устраняется из результата измерения.
Введением поправки устраняется влияние только одной составляющей
систематической погрешности, поэтому может потребоваться вводить большое
число поправок в результаты измерения.
При этом следует помнить, что вследствие ограниченной точности
определения поправок накапливаются случайные погрешности и дисперсия
результата измерения увеличивается.
25

26.

Действительно, при исправлении результата x путем введения m поправок
cj, j = 1, 2, …, m, исправленный результат имеет вид
m
x x c j .
j 1
При этом дисперсия исправленного результата становится равной
m
S 2 ( x) S 2 ( x ) S c2j ,
j 1
где
S 2 ( x ) – оценка дисперсии неисправленного результата;
S c2j – оценка дисперсии j-ой поправки.
Таким образом, уменьшение систематической погрешности сопровождается
m
увеличением случайной составляющей за счет
S c2 .
j 1
j
26

27.

Таким образом, при введении поправки следует учитывать следующие
соображения.
1. Поправку имеет смысл вводить в результат измерения, если оценка СКО
поправки
Sc
m
2
S
cj
значительно
меньше
систематической
j 1
составляющей погрешности.
2. Погрешность результата обычно выражается не более чем двумя
значащими цифрами. Поэтому, если поправка не превышает 0,5
младшего разряда погрешности результата, то она будет потеряна при
округлении и вводить ее не имеет смысла.
27

28.

Порядок обработки
косвенных измерений
28

29.

Пример. Измерения
результат:
ребер
прямоугольного
параллелепипеда
дали
x = (50,0 ± 0,5) мм
y = (10,0 ± 0,5) мм
z = (40,0 ± 0,5) мм
Чему равен объем детали?
Порядок обработки косвенных измерений приведен в документе:
МИ 2083-90 ГСИ. Измерения косвенные. Определение результатов
измерений и оценивание их погрешностей.
29

30.

При косвенных измерениях искомое значение величины y находят
расчетом на основе прямых измерений величин xi , связанных с
измеряемой величиной известной зависимостью (уравнением
измерений):
y f ( x1, x2 ,..., xm )
(*)
Результатом косвенного измерения является оценка величины y,
которую находят подстановкой в формулу (*) оценок аргументов xi .
Поскольку каждый из аргументов xi измеряется с некоторой
погрешностью, то задача оценивания погрешности результата сводится
к суммированию погрешностей измерения аргументов.
Вклад отдельных погрешностей измерения
погрешность результата зависит от вида функции (*).
аргументов
Косвенные измерения делят на линейные и нелинейные.
30
в

31.

Линейные косвенные измерения
При линейных косвенных измерениях уравнение измерений (*) имеет
вид:
m
y bi xi ,
i 1
где bi – постоянные коэффициенты при аргументах xi .
Любые другие виды функциональной зависимости (*) относят к нелинейным
косвенным измерениям.
Погрешности измерения аргументов могут быть заданы
своими границами хi или
доверительными границами хi (Рi), где Рi – доверительная вероятность.
При малом числе аргументов (меньше пяти) простая оценка
погрешности результата y получается простым (алгебраическим)
суммированием предельных погрешностей (без учета знака), т.е.
подстановкой границ х1, х2,…, хm в выражение:
y x1 x2 ... xm .
31

32.

Однако эта оценка является завышенной, т.к. предполагает, что
погрешности измерения всех аргументов одновременно имеют
максимальное значение и совпадают по знаку. Вероятность такого
совпадения практически равна нулю.
Для нахождения более реалистичной оценки переходят к
статиcтическому (геометрическому) суммированию погрешностей
аргументов по формуле:
m
y k bi2 xi2 ,
i 1
где
k – коэффициент, определяемый принятой доверительной
вероятностью
(Р = 0,9 при k = 0,95;
Р = 0,95 при k = 1,1;
Р = 0,99 при k = 1,4).
32

33.

Если погрешности измерения аргументов заданы доверительными
границами с одинаковыми доверительными вероятностями Рд, то при
нормальном распределении этих погрешностей доверительные границы
результата находят по формуле:
y
m
i 1
[bi xi ( Pд )]2
С учетом корреляции между составляющими итоговая погрешность
имеет вид:
m
y k
i 1
где
bi2 xi2
m m
bib j xi x j ij
i 1 j 1
j i
m – число суммируемых составляющих погрешностей;
ij – коэффициент корреляции между i- и j-й составляющими.
33

34.

Нелинейные косвенные измерения
Характеризуются тем, что результаты измерений аргументов
подвергаются функциональным преобразованиям.
Поэтому при нелинейных косвенных измерениях отказываются от
интервальных оценок погрешности результата, ограничиваясь
приближенной оценкой ее границ.
В основе приближенного оценивания погрешности нелинейных
косвенных измерений лежит линеаризация функции (*), а дальнейшая
обработка проводится как при линейных косвенных измерениях.
34

35.

Метод линеаризации состоит в том, что нелинейная функция, связывающая
измеряемую величину с аргументами, разлагается в ряд Тейлора:
m
f
y f ( x1 , x2 ,..., xm ) f ( x1 , x2 ,..., xm ) xi R ,
i 1 xi
где f / xi – первая частная производная от функции f по
аргументу xi (чувствительность), вычисленная в точке
x1 , x2 ,..., xm , определяемой результатами измерений аргументов;
xi xi xi – погрешности измерений аргументов;
1 m 2 f
R
xi x j – остаточный член ряда.
2 i , j 1 xi x j
Метод линеаризации применим, если остаточным членом ряда можно
пренебречь при условии
2
f
2
R 0,8
S
(
x
)
,
i
x
i
i 1
где S ( xi ) – СКО случайной погрешности измерений аргумента xi.
m
Брук Тейлор
(1685-1731)
35

36.

Упрощенный расчет погрешностей косвенных измерений
Оценить абсолютную погрешность косвенной величины y при можно по формуле
y | y1 | | y2 | ... | ym | ,
где
f
f
f
y1
x1 , y2
x2 , ...., ym
xm .
x1
x2
xm
Вычисления существенно упрощаются для простейших функций f.
Так, если y x1 x2 ... xm , то все частные производные
y x1 x2 ... xm .
То есть абсолютная погрешность
абсолютных погрешностей слагаемых.
Если y x1 x2 ... xm , то получаем
суммы
f
равны 1 и
xi
аргументов
равна
сумме
x
y x1 x2
... m , откуда
y
x1
x2
xm
y 1 2 ... m .
То есть относительная погрешность произведения аргументов равна сумме
относительных погрешностей слагаемых.
36

37.

Вообще, если функция выражается в виде произведения:
y x1 x 2 xm ,
где , , γ _ положительные или отрицательные известные константы, то
логарифмирование с последующим дифференцированием дает
ln y = ln x1 + ln x2 +…+ ln xm,
xm
y
x1
x2
y
...
1 2 ... m .
y
x1
x2
xm
То есть чувствительности к изменению погрешностей xi равны
показателям соответствующих степеней.
37

38.

Формулы расчета погрешностей косвенных измерений для
функции двух аргументов
y f ( x1, x2 ) Абсолютная погрешность Относительная погрешность
| x1 | | x2 |
x1 x2
| x1 | | x2 |
1
x1 x2
| x1 | | x2 |
x1 x2
| x1 | | x2 |
2
x1 x2
3
x1 x2
x1 x2 x2 x1
4
x1
x2
x1 x2 x2 x1
5
6
x
p
p
x
x22
| px
1
x
p
p 1
x |
1
1
p
x
x1 x2
1 2
x1
x2
x1 x2
1 2
x1
x2
p
x
p
x
1 x
p x
p
38

39.

Важно:
1. Случайные
погрешности
измерений
могут
равновероятно
быть
положительными и отрицательными. Поэтому и при сложении, и при
вычитании измеренных величин абсолютные погрешности складываются.
2. При вычитании двух величин относительная погрешность содержит в
знаменателе разность двух величин. Если эти величины близки, то
относительная погрешность разности может значительно превышать
относительную погрешность каждой величины в отдельности. Во избежание
потери точности следует избегать таких измерений и вычислений, когда
приходится вычитать близкие по значению величины.
3. При умножении и делении величин складываются относительные
погрешности.
4. То есть когда расчетная формула является одночленом, а суммы и разности
если и присутствуют, то в виде отдельных множителей, проще сначала
вычислить не абсолютную, а относительную погрешность величины y. Если же
расчетная формула имеет вид многочлена, целесообразно начинать с расчета
абсолютной погрешности.
5. При возведении в степень p, такую что |p| 1, относительная погрешность
увеличивается в |p| раз.
39

40.

Учет погрешностей констант
Если в расчетную формулу для y входят, наряду с измеренными величинами,
табличные данные или справочные константы, то при вычислении
погрешности y следует учитывать и их погрешности. Если их погрешность не
указана специально, то обычно считается, что она не превышает половины
младшего разряда.
Пример. Для ускорения свободного падения
g = 9,8 м/с2 g = 0,05 м/c2,
а для
g = 9,81 м/с2 g = 0,005 м/c2.
Пример. Необходимо определить длину внешней окружности вала путем
измерения диаметра вала с последующим вычислением длины окружности по
формуле
L = D.
Погрешность измерения должна быть не более 0,2 %. Требуется выбрать средство
и метод измерения, обеспечивающие заданную точность.
40

41.

Решение. Диаметр вала D = 1,278 мм был измерен рычажной скобой с
погрешностью ±0,002 мм.
Пусть значение = 3,14. Его погрешность следует оценить значением 0,005.
Тогда погрешность измерения длины окружности вычисляется следующим
образом
L D 0,005 0,002
0,0016 0,0016 0,0032 0,32 %.
L
D
3,14 1,278
Это значение значительно превышает допустимое, равное 0,2 %.
Если значение записать как 3,142, то его погрешность следует принять
равной 0,0005. Тогда погрешность измерения L рассчитывается как:
L D 0,0005 0,002
0,00016 0,0016 0,000176 0,2%,
L
D
3,142 1,278
что соответствует требованиям поставленной задачи.
41