Похожие презентации:
Потоки в сетях
1.
ИСОПОТОКИ В СЕТЯХ
Пусть каждой дуге ( x, y )
ориентированного графа G (V , E )
поставлено
в
соответствие положительное рациональное число
интерпретируемое
как
c ( x, y ) ,
s, t V
пропускная способность дуги. Зафиксируем две вершины
. Вершину s назовём
источником, а t − стоком.
Стационарным потоком величины
из вершины s в вершину t на сети G (V , E )
называется функция f ( x, y ) , заданная на всех дугах и удовлетворяющая следующим
условиям:
0 f ( x , y) c ( x , y ), ( x , y) E
(1)
, если x s,
(2)
f ( x, y) f ( y, x) 0, если x s, t,
y O ( x )
y O ( x )
, если x t.
Условия (1) означают, что поток по каждой дуге не должен превышать ее пропускную
способность.
Условие (2) показывают, что для источника суммарное количество входящего и выходящего
потока должно быть равно – величине потока в сети. Аналогично для стока суммарное
количество выходящего и входящего потока также равно . Для всех промежуточных вершин
сети суммарное количество входящего и выходящего потока должно быть равно нулю.
2.
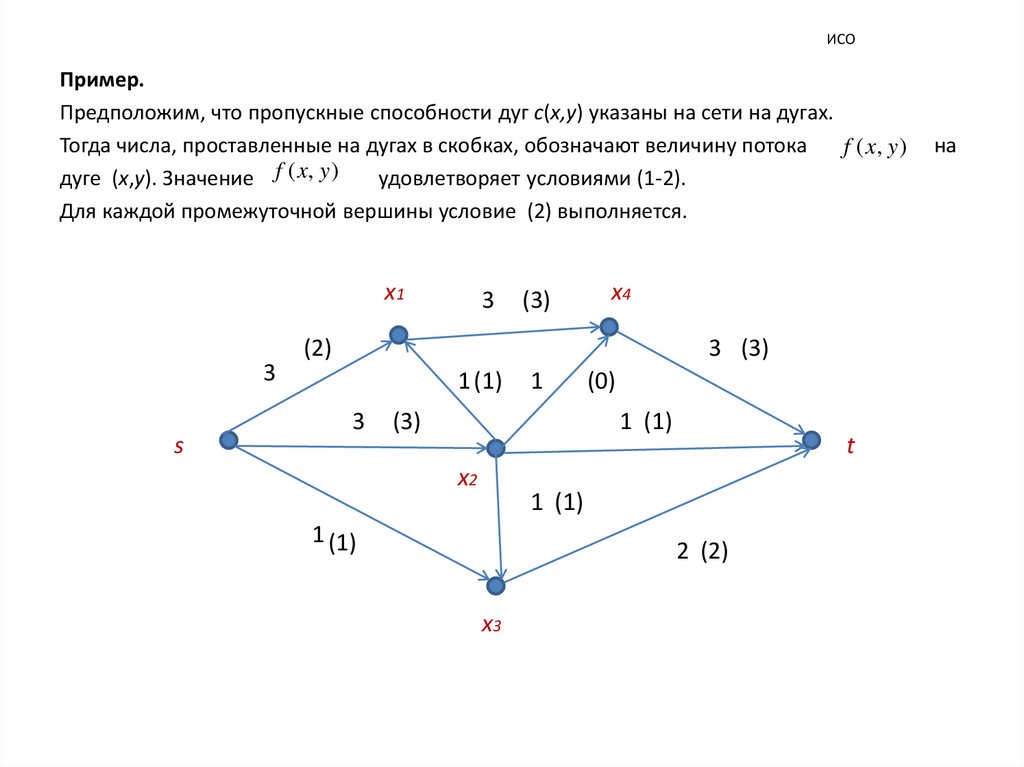
ИСОПример.
Предположим, что пропускные способности дуг c(x,y) указаны на сети на дугах.
Тогда числа, проставленные на дугах в скобках, обозначают величину потока
f ( x, y )
дуге (x,y). Значение f ( x, y )
удовлетворяет условиями (1-2).
Для каждой промежуточной вершины условие (2) выполняется.
x1
3
s
3
(3)
x4
(2)
3 (3)
1 (1)
3
1
(3)
(0)
1 (1)
x2
t
1 (1)
1 (1)
2 (2)
x3
на
3.
ИСОКлассическая задача о максимальном потоке
В сети с заданными на ее дугах пропускными способностями можно построить сколь
угодно много потоков, т.е. указать как угодно много функций f ( x, y )
,
удовлетворяющих условиям (1)-(2).
• Задача состоит в нахождении для данной сети стационарного потока максимально
возможной величины.
Задача всегда имеет решение.
• Назовем некоторую цепь из s в t увеличивающей поток, если на всех дугах,
совпадающих по направлению от s к t (прямые дуги), выполняется неравенство
f ( x, y ) c( x, y ) , а на всех дугах, не совпадающих по направлению (обратные дуги)
.
f ( x, y ) 0
Теорема. Поток является максимальным, тогда и только тогда, когда в сети не
существует ни одной цепи, увеличивающей поток.
• Разрезом сети, отделяющим источник s от стока t, будем называть множество дуг, и
обозначать ( X1 , X1 )
, такое, что каждая дуга начинается в множестве X и
X
оканчивается во множестве
. Кроме того,
s X , t X , X X V , X X O/ .
Для построения произвольного разреза достаточно задать множество вершин X , а
будет дополнением X до всего множества V
.
X
4.
ИСОx1
3
s
3
(1)
x4
(2)
3 (1)
1 (1)
3
1
(3)
(0)
1 (1)
x2
t
1 (1)
1 (0)
2 (1)
x3
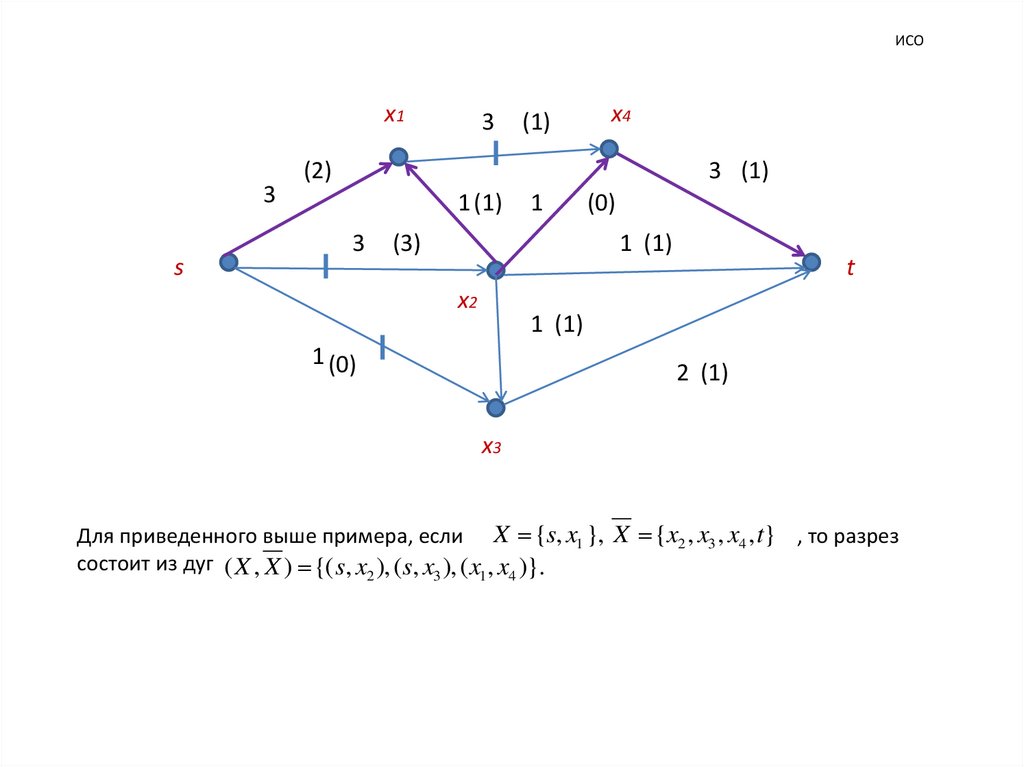
Для приведенного выше примера, если X {s, x1 }, X {x2 , x3 , x4 , t} , то разрез
состоит из дуг ( X , X ) {( s, x2 ), (s, x3 ), ( x1 , x4 )}.
5.
ИСОТеорема (Форда-Фалкерсона). Для любой сети с источником s и стоком t максимальная
величина потока из s в t равна минимальной пропускной способности разреза,
отделяющего s от t.
Доказательство: Для того, чтобы доказать утверждение достаточно для какого-то
потока подобрать разрез , отделяющий s от t, при котором величина потока равняется
пропускной способности этого разреза. В самом деле, если будет выполняться равенство
величины потока и пропускной способности разреза, то потока с большей величиной быть
не может. Не может существовать и разреза с меньшей пропускной способностью.
(X , X )
Предположим, что f – максимальный поток. Построим разрез
,
используя следующее правило:
a) s будем относить к множеству X, т.е.
s X ;
x X и для дуги (x,y) выполняется неравенства f(x,y)<c(x,y), то y X .
Аналогично, если по дуге (y,x) имеет ненулевой поток , т.е. f(x,y)>0, то y X . В
итоге применения правила будет построено множество X и для того, чтобы это множество
определяло разрез, отделяющий s от t, необходимо показать, что сток t X
.
б) если
6.
ИСОПредположим противное -
t X
. Это означает, что в сети существует цепь вида,
(s,x1,…xn,t), ведущая из вершины s в вершину t, такая, что на каждой дуге вида (xi,xi+1) с
ориентацией, совпадающей с направлением пути от s к t, должно выполняться неравенство
f(xi,xi+1)<c(xi,xi+1) (на основании правила). Обозначим множество прямых дуг этой цепи
через A. Аналогично, для каждой дуги вида (xi+1,xi ) с ориентацией, противоположной
направлению пути от s к t, должно выполняться неравенство f(xi,xi+1). Пусть это множество
дуг B. Вычислим:
1 min [c( xi , xi 1 ) f ( xi , xi 1 )]
( xi , xi 1 ) A
,
2 min [ f ( xi 1 , xi )].
( xi 1 , xi ) B
0
Найдем min( 1 , 2 )
. Очевидно, что
. Проведем изменение
потока на выбранной цепи от s к t.
На всех дугах, направления которых совпадает с направлением от s к t увеличиваем
значение на . На всех дугах, обратных направлению от s к t, уменьшим значение на
.
Легко видеть, что в результате такого преобразования значений потоков на выбранной
цепи новые значения будут образовывать поток, общая величина потока в сети увеличится
на величину 0 .
7.
ИСОТак как по предположению поток в сети максимальный, то получилось противоречие. Оно
возникло из-за того, что мы предположили, что t X
. Следовательно, t X
.
Таким образом, множество X определяет разрез , отделяющий s от t. Для всех
f ( x, y ) c ( x , y )
должно выполняться строгое равенство
.
( x, y ) ( X , X )
Аналогично, для дуг вида
должно выполняться равенство
( y, x) ( X , X )
f ( y, x) 0 . Приходим к равенству:
f ( X , X ) c( X , X )
.
Таким образом, мы нашли разрез, пропускная способность которого совпадает с величиной
потока в сети. Теорема доказана.
Алгоритм Форда-Фалкерсона для нахождения максимального потока начинает свою
работу с произвольного начального потока в сети. Например, нулевого потока.
Алгоритм на каждой итерации состоит из двух этапов.
Этап 1 (расстановка меток). На этом этапе ищется цепь, увеличивающая поток. Поиск
такой цепи осуществляется с помощью расстановки меток. В процессе расстановки меток
каждая вершина может находиться в одном из трех состояний: «непомеченная»,
«помеченная и не просмотренная», «помеченная и просмотренная».
В начале все вершины непомечены.
Источник s получает метку вида (–, ). После этого s переходит в состояние «помечен
и не просмотрен».
8.
ИСОПусть существует несколько помеченных и не просмотренных вершин. Выберем среди
них вершину х. Просматриваем непомеченные вершины y O+(x) с проверкой условия
f ( x, y ) c( x, y ) . Если для дуги ( x, y ) , неравенство имеет место, то вершина y
( x , ( y))
получает метку
, где
( y ) min[ ( x), c( x, y ) f ( x, y)]
.
Затем просматриваем непомеченные вершины y O-(x) и проверяем условие
f ( y, x) 0 . Если для дуги (y, x) неравенство выполняется, то вершина y получает пометку
( x , ( y)) , где
( y ) min[ ( x), f ( y, x)].
После этого вершина x переходит в состояние «помеченная и просмотренная».
Далее выбирается очередная помеченная и не просмотренная вершина, и для нее
повторяются все описанные выше действия. Причем придерживаемся правила: «первый
помечен − первый просмотрен».
Расстановка пометок продолжается до тех пор, пока или будет помечена вершина t, или
сток t никоим образом пометить нельзя.
В первом случае найден увеличивающий путь. Переходим к этапу 2.
Во втором случае алгоритм заканчивает свою работу и это означает, что максимальный
поток найден на предыдущей итерации. При этом определяется соответствующий
полученному максимальному потоку минимальный разрез сети. Разрез будет состоять из
дуг, идущих из помеченных вершин в непомеченные на последней итерации вершины, при
этом все дуги минимального разреза насыщены.
9.
ИСОЭтап 2 (увеличение потока). Вершина y может получить одну из двух пометок
( x , (t ))
или
( x , (t ))
. Если y имеет пометку
( x , (t ))
, поток
ε(t) . Если t имеет пометку , ( x , (t )) поток
по дуге (x,y) , уменьшается на значение ε(t) .
Начинаем со стока t и переходим к вершине x, которая указана в пометке вершины t.
по дуге (x,y) увеличивается на значение
Изменение потоков на величину по дугам повторяется до тех пор, пока не будет достигнута
вершина s.
Стираем у вершин все метки и возвращаемся к этапу 1 с новым увеличенным потоком.
В изложенном варианте сложность алгоритма Форда-Фалкерсона равна O(|V | |E |2).
10.
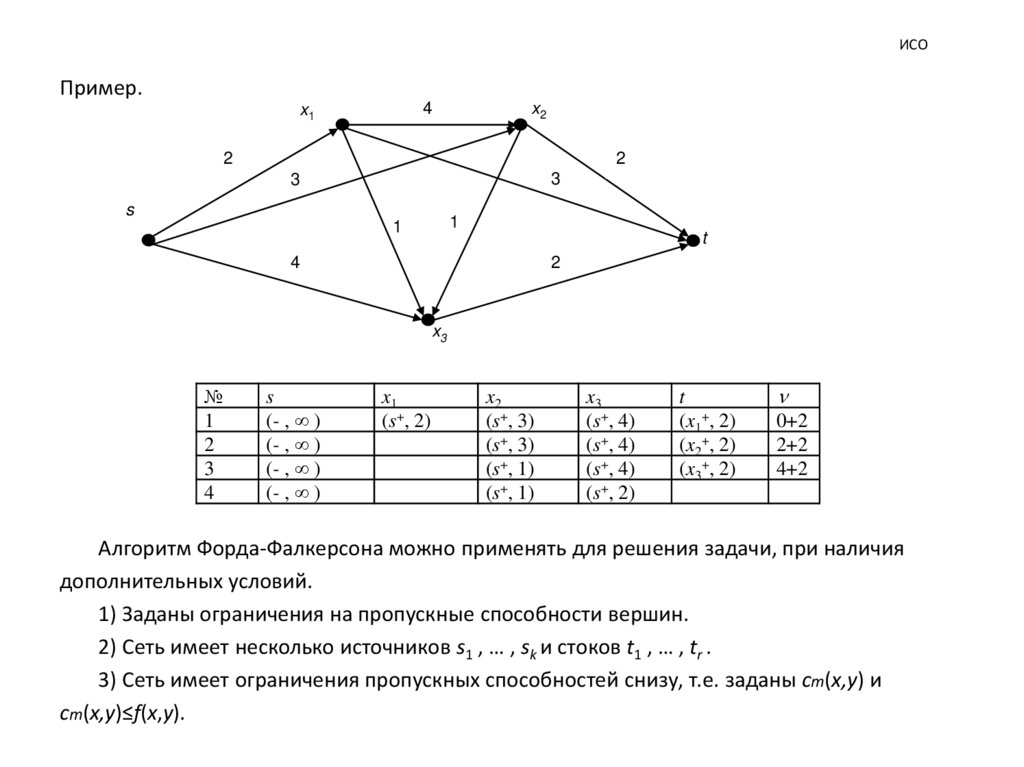
ИСОПример.
4
x1
x2
2
2
3
3
s
1
1
t
4
2
x3
№
1
2
3
4
s
(- , )
(- , )
(- , )
(- , )
x1
(s+, 2)
x2
(s+, 3)
(s+, 3)
(s+, 1)
(s+, 1)
x3
(s+, 4)
(s+, 4)
(s+, 4)
(s+, 2)
t
(x1+, 2)
(x2+, 2)
(x3+, 2)
0+2
2+2
4+2
Алгоритм Форда-Фалкерсона можно применять для решения задачи, при наличия
дополнительных условий.
1) Заданы ограничения на пропускные способности вершин.
2) Сеть имеет несколько источников s1 , … , sk и стоков t1 , … , tr .
3) Сеть имеет ограничения пропускных способностей снизу, т.е. заданы cm(x,y) и
cm(x,y)≤f(x,y).
11.
ИСОЗадача о многополюсных путях с максимальными пропускными способностями
Пусть дана ориентированная сеть с пропускными способностями дуг ≥ 0, (x, y) E. В задаче о
многополюсных путях с максимальными пропускными способностями необходимо для
каждой пары вершин x, y V найти соединяющий x и y путь (если он существует), имеющий
максимальную пропускную способность.
Пронумеруем вершины сети и построим матрицу пропускных способностей С= | cij | nxn
(n = |V | ) с элементами
0,i j ,
cij c( xi , x j ) , ( xi , x j ) E ,
, i j , ( xi , x j ) E ,
и матрицу путей T = | tij | nxn с элементами tij = j .
Алгоритм решения задачи о многополюсных путях с максимальными пропускными
способностями подобен алгоритму Флойда поиска минимальных путей для каждой пары
вершин сети.
Шаг 1. Положить k = 0, и положить матрицы C 0 | cij0 | nxn , T 0 | tij0 | nxn с cij0 cij , tij0 tij , i, j 1, n .
Шаг 2. Построить матрицы C k 1 | cijk 1 | nxn , T | t | по матрицам C k | cijk | nxn и T k | tijk | nxn ,
вычисляя их элементы по формулам:
.
c k , i k 1, j 1, n ,
k
k 1
k
k 1
cij cijk , j k 1, i 1, n ,
k
k
k
max { cij ; min [ cik 1 , c k 1 } , i k 1, j k 1 ,
k 1
ij
ij
t
k 1
ij
nxn
tij , если cij cij ,
k 1
k
j , если cij cij .
12.
ИСОШаг 3. Если k + 1 < n , то положить k := k +1 и перейти к шагу 2.
Если k+1 = n , то матрица C n даёт искомые максимальные пропускные способности для пар
вершин сети.
Путь с максимальной пропускной способностью от вершины xi к вершине xj строится по
n
элементам матрицы Tn . Элемент tij m
указывает промежуточную вершину xm в пути от
n
t
вершины xi к вершине xj . Находим im
и tmjn
, которые указывают очередные
n
n
tim m tmj j
промежуточные вершины. Если
, то вершина xm непосредственно
следует за вершиной xi (непосредственно предшествует вершине xj ). Процесс завершаем
при получении номера вершины непосредственно следующей за xi и номера вершины
непосредственно предшествующей xj .
Пример. Решить задачу о многополюсных путях с максимальными пропускными
способностями для следующей сети.
x2
2
x5
11
12
x1
30
11
19
x3
x4
Поскольку сеть является неориентированной, то заменяем каждое ребро парой
противоположно направленных дуг. В результате получим матрицу пропускных
способностей и матрицу путей:
13.
ИСОC C0
0 11
30
11 0
12
2
30 0
19
12 19
0
11
2 11
0
1 2
1 2
0
T T 1 2
1 2
1 2
3
3
3
3
3
4
4
4
4
4
5
5
5
5
5
1
1
1
T 1
1
1
3
1
3
3
3
4
4
4
4
4
5
5
5
5
5
На последующих итерациях получим
0 11
30
11 0
11 12
2
1
C 30 11
0
19
12 19
0
11
2 11
0
2
2
1
2
2
0 11 30 11 2
11 0 11 12 2
2
C 30 11 0 19 2
11 12 19 0 11
2 2
2 11 0
1 2
1 2
2
T 1 1
2 2
2 2
3
1
3
3
2
2
4
4
4
4
2
5
2
5
5
0 11 30 19 2
11 0 11 12 2
3
C 30 11 0 19 2
19 12 19 0 11
2 2
2 11 0
1 2
1 2
3
T 1 1
3 2
2 2
3
1
3
3
2
3
4
4
4
4
2
5
2
5
5
14.
ИСО0 12
12 0
4
C 30 12
19 12
11 11
30
12
0
19
11
19
12
19
0
11
11
11
11
11
0
1 4
4 2
4
T 1 4
3 2
4 4
3
4
3
3
4
3
4
4
4
4
4
4
4
5
5
0 12
12 0
5
C 30 12
19 12
11 11
30
12
0
19
11
19
12
19
0
11
11
11
11
11
0
1 4
4 2
5
T 1 4
3 2
4 4
3
4
3
3
4
3
4
4
4
4
4
4
4
5
5
Матрица C 5 даёт значения максимальных пропускных способностей путей между
вершинами. Например, максимальная пропускная способность путей между третьей и
пятой вершинами равно 11. Сам путь с указанной пропускной способностью строим по
матрице T4. Получим x3 x4 x5 .











 Интернет
Интернет