Похожие презентации:
Логическое программирование
1.
Уфимский государственный авиационныйтехнический университет
Факультет информатики и робототехники
Кафедра вычислительной математики и кибернетики
Логическое
программирование
Д.т.н., профессор кафедры ВМиК Ризванов Дмитрий Анварович
2. Литература по дисциплине
Д.А. Ризванов, Д.В. Попов, Г.А. Макеев. Функциональное и логическое
программирование. Математические основы и языковая семантика:
учебное пособие. – Уфа: УГАТУ, 2009. – 160 с.
И.Братко. Программирование на языке Пролог для искусственного
интеллекта. М.: Мир. 1990, 2007.
Дж.Стобо. Язык программирования Пролог. "Радио и связь". М.1993.
У.Клоксин, К.Меллиш. Программирование на языке Пролог. "Мир".1987.
Дж.Малпас. Реляционный язык Пролог и его применение.
"Наука".М.1990.
А.Янсон. Турбо-Пролог в сжатом изложении. "Мир". М. 1991
Ц.Ин,Д.Соломон. Использование Турбо-Пролога. "Мир".М.1993.
Язык Пролог в пятом поколении ЭВМ. Сб.статей. "Мир".М.1988
2
3.
Эпиграф4. Основные конструкции логической программы
ЛП состоит из предложений, которые описывают знания о решаемой задаче.Предложение конструируется из объектов и отношений между ними.
Объекты.
Конкретное множество объектов образует проблемную область.
Например, для задачи f(x) -> min множество всех чисел образует проблемную область,
если f(x) определена.
Конкретные объекты образуют множество индивидуумов.
Конкретные объекты и конкретные отношения это константы.
Имена констант это атомы.
Различают атомы простые и составные.
Например, «мир» – простой, «студент(петров)» - составной.
В общем виде структура имени имеет вид: f(t1,…,tn) где f – функтор, ti – аргументы.
Отношения.
Рассмотрим запись «сессия(экзамен(мат, физ, прогр), весна)»
В основе представления о смысле имен сессии и экзамена лежат конкретные множества
наборов объектов. Заданием этого множества можно формализовать понятие
«экзамены».
Например, экзамены = { (мат, физ, прогр), (фил, псих, экол), … }
Это пример трехместного отношения. N- местное отношение – это множество кортежей
для фикс. N.
4
5. Основные конструкции логической программы (2)
Предикаты.В логике отношение называют предикатом.
Имя отношения – предикатный символ.
Запись P(t).
Понимание:
1. Элементы кортежа t принадлежат отношению с именем P или:
2. Высказывание Р верно для элементов кортежа t.
Предложение состоит из:
• Логических связок (и), (или), (не), (если), (тождественно).
• Предикатов.
• Формул:
Каждый предикат – формула.
Если F1, F2 – формулы, то
(F1) – формула.
F1 F2, F1 F2, F1, F1 F2, F1 F2 – тоже формулы.
Например.
Студент-ФИРТ(петров) – формула.
Студент-УГАТУ(петров) Студент-ФИРТ(петров) – формула.
Замечание. «петров» - конкретный объект, поэтому с малой буквы.
5
6. Основные конструкции логической программы (3)
Переменные, термы, предложения.Логические переменные используются при формулировке утверждения обо
всех объектах данной совокупности.
Имя переменной начинается с заглавной буквы.
Терм – либо константа, либо переменная, либо кортеж, перед которым стоит
функтор.
Предикат – кортеж, перед которым стоит предикатный символ.
Формула – предикат либо одно из выражений (F1), θ F1, где θ – любой из
кванторов.
Предложение – формула, каждое вхождение переменной которой находится в
области действия квантора по ней.
Замечание. Логический терм – единственная структура данных в ЛП.
Предикаты выражают отношения между объектами, а предложения описывают
логические свойства отношений.
6
7. Виды предложений ЛП
1.Факты2.Правила
3.Вопросы
7
8. Факты
Факт P(t1,…,tn). – простейшее предложение, используемое для того, чтобыможно было утверждать, что высказывание о принадлежности объекта ti
некоторому отношению P истинно.
Например, факультет-УГАТУ(фирт).
Универсальный факт:
«все студенты МО владеют английским языком»: влад-англ-яз(Студ, мо).
Простейшей ЛП является простейшая БД.
Создание БД начинается с создания реляционной схемы для каждого
отношения.
Например, книга(Автор, Название, Издательство, Год):
книга(братко, программирование-на-языке-пролог, мир, 1990).
8
9. Правила
Правила – предложения вида P(t1,…,tn) a1(t1,…,tr), a2(t1,…,ts), …, am(t1,…,tq).Например, «некто получает повышенную стипендию, если некто студент,
сдавший все экзамены на отлично»:
получ-повыш-стип(X) сдал-все-экз(X), экз(X,5,5,5,5).
Замечания.
1. Факт – простейший случай правила.
2. В ЛП правила называют аксиомами, а совокупность фактов и правил –
гипотезами.
9
10. Вопросы
Вопросы – служат для извлечения информации из ЛП.Различают простые и конъюнктивные.
Вид: ? P(t). Здесь Р – цель, поэтому вопросы еще называют целевыми
утверждениями.
Конъюнктивные: ? поэт(ломоносов), химик(ломоносов), спортсмен(ломоносов).
Процедура поиска ответа на простой вопрос состоит в отыскании факта
P(t1,…,tn). Поиск состоит в том, чтобы определить, является ли вопрос
логическим следствием программы.
При поиске ответа на простой вопрос используются простейшие правила
вывода. Правила основаны на теореме “из Р выводимо Р”. Если факт,
тождественный вопросу, найден, то ответ “да” иначе “нет”.
Если получен ответ “нет”, то это означает, что факт Р не содержится в БД.
При этом возможно, что информация в факте Р верная.
Например, ? книга(агафонов, логическое-программирование,наука, 1988) БД,
хотя информация верная.
10
11. Вопросы (2)
Вопросы с переменными служат для представления совокупности вопросов.Например, ? книга(X, Y, Z, 1990).
Поиск ответа на вопрос заключается в определении, существуют ли такие
значения переменных, при которых вопрос будет логическим следствием
программы. Такие вопросы называются экзистенциональными.
Понятие вопроса связано с понятием общих переменных.
Общие переменные – переменные, входящие в две или более различные цели
вопроса.
Например, likes("Саша",X) likes("Зина",X), likes("Нина",X).
11
12. Программирование на языке Пролог
В отличие от алгоритмических, процедурных языковпрограммирования, Пролог относится к логическим, декларативным языкам.
При использовании языков первой группы программист задает
машине способ решения поставленной задачи, называемый алгоритмом.
Программы на Прологе содержат только описания (декларации)
отношений между объектами, которые необходимы для решения задачи.
Способ решения задачи выбирает сама машина. Поэтому программы на
Прологе бывают понятнее и много короче, чем на алгоритмических языках
программирования.
12
13. Структура логической программы
Domains% название раздела типов данных
name = symbol
Predicates
% название раздела с описанием предикатов
likes(name, name)
Сlauses
% название раздела с фактами и правилами
likes("Зина", "мороженое").
likes("Зина", "чтение").
likes("Нина", "мороженое").
likes("Нина", "чтение").
likes("Саша", Х) :- likes("Зина", Х), likes("Нина", Х).
Goal
% название раздела с вопросом
likes("Саша",Y), write(Y), nl.
13
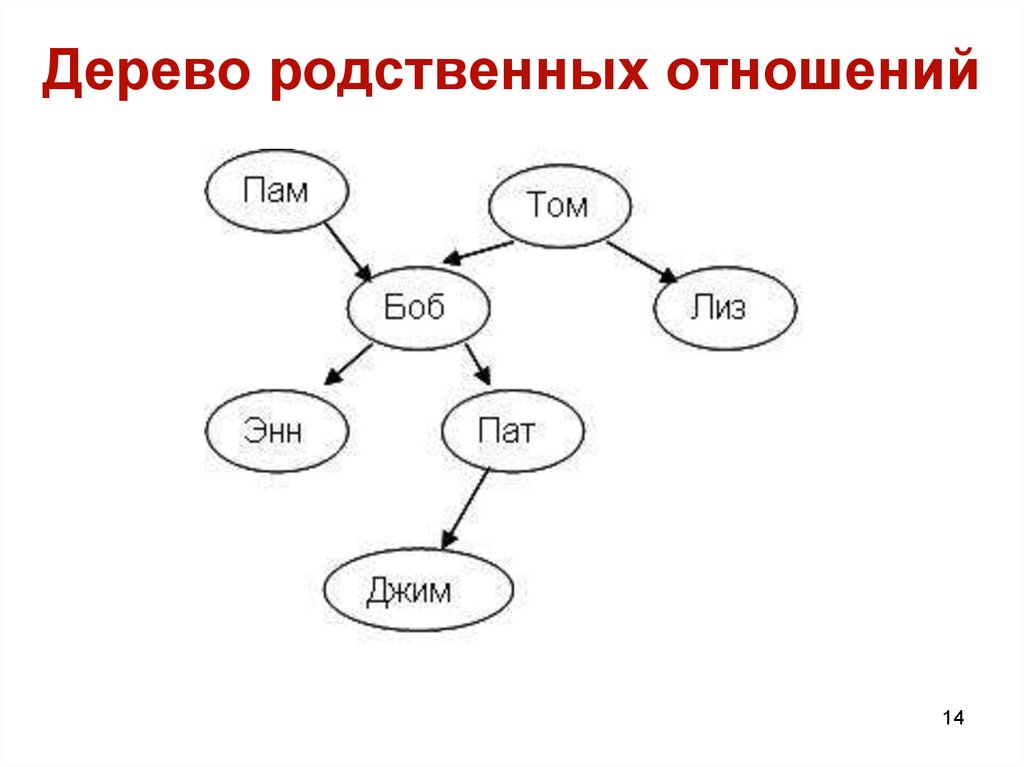
14. Дерево родственных отношений
1415. Программа «Дерево родственных отношений»
PredicatesРодитель(name, name).
Run.
Clauses
Родитель(пам, боб).
Родитель(том, боб).
Родитель(том, лиз).
Родитель(боб, энн).
Родитель(боб, пат).
Родитель(пат, джим).
Run :- Родитель(боб, пат).
Goal
Run.
Ответ
Yes
15
16. Программа «Дерево родственных отношений»
PredicatesРодитель(name, name).
Run.
Clauses
Родитель(пам, боб).
Родитель(том, боб).
Родитель(том, лиз).
Родитель(боб, энн).
Родитель(боб, пат).
Родитель(пат, джим).
Run :- Родитель(лиз, пат).
Goal
Run.
Ответ
No
16
17. Программа «Дерево родственных отношений»
Вопрос: «Кто является родителем родителя Джима»17
18. Программа «Дерево родственных отношений»
Вопрос: «Кто является родителем родителя Джима»Predicates
Родитель(name, name).
Run.
Run(name, name).
Clauses
Родитель(пам, боб).
Родитель(том, боб).
Родитель(том, лиз).
Родитель(боб, энн).
Родитель(боб, пат).
Родитель(пат, джим).
Run :- Родитель(боб, пат).
Run :- Родитель(лиз, пат).
Run(X,Y) :- Родитель(Y, джим), Родитель(X, Y).
Goal Run(X,Y).
Ответ
X=боб, Y=пат.
18
19. Цели в Пролог-программе
• Внутренние• Пролог находит только первое решение с полученными значениями
переменных
• Внешние
• Пролог находит все достижимые цели
19
20. Управление откатом
Предикат cut!
Этот предикат, вычисление которого всегда завершается успешно, заставляет
внутренние программы сопоставления «забыть» все указатели отката,
установленные во время попыток вычислить предыдущие подцели.
pr:- a, b, !, c.
При вычислении подправилa а, затем b осуществляется последовательный
поиск решений с откатами до тех пор, пока не будут удовлетворены эти
подцели; далее произойдет успешное завершение предиката отсечения !;
затем начнется вычисление подцели с, но здесь откаты возможны только при
поиске решений для с и благодаря отсечению становятся невозможными
откаты для нового поиска альтернативных решений для подцелей a и b.
20
21. Управление откатом
Run :- Родитель(X, Y).Goal
Run.
Run(X, Y) :- Родитель(X, Y).
Goal
Run(X, Y).
Run(X, Y) :- Родитель(X, Y), !.
Goal
Run(X, Y).
21
22. Управление откатом
Run :- Родитель(X, Y).Goal
Run.
% будет одно – первое согласование
Run(X, Y) :- Родитель(X, Y).
Goal
Run(X, Y).
Run(X, Y) :- Родитель(X, Y), !.
Goal
Run(X, Y).
22
23. Управление откатом
Run :- Родитель(X, Y).Goal
Run.
% будет одно – первое согласование
Run(X, Y) :- Родитель(X, Y).
Goal
Run(X, Y).
% будет 6 согласований
Run(X, Y) :- Родитель(X, Y), !.
Goal
Run(X, Y).
23
24. Управление откатом
Run :- Родитель(X, Y).Goal
Run.
% будет одно – первое согласование
Run(X, Y) :- Родитель(X, Y).
Goal
Run(X, Y).
% будет 6 согласований
Run(X, Y) :- Родитель(X, Y), !.
Goal
Run(X, Y).
% будет 1 согласование
24
25. Программа «Дерево родственных отношений»
Расширим нашу программу с помощью новых правил:добавим информацию о том, каков пол людей,
участвующих в отношении Родитель.
25
26. Программа «Дерево родственных отношений»
Расширим нашу программу с помощью новых правил:добавим информацию о том, каков пол людей,
участвующих в отношении Родитель.
1-й способ:
Женщина(пам).
Мужчина(том).
Мужчина(боб).
Женщина(лиз).
Женщина(пат).
Женщина(энн).
Мужчина(джим).
26
27. Программа «Дерево родственных отношений»
Расширим нашу программу с помощью новых правил:добавим информацию о том, каков пол людей,
участвующих в отношении Родитель.
1-й способ:
Женщина(пам).
Мужчина(том).
Мужчина(боб).
Женщина(лиз).
Женщина(пат).
Женщина(энн).
Мужчина(джим).
2-й способ:
Пол(пам, женский).
Пол(том, мужской).
…
Женщина(X) :- Пол(X, женский).
Мужчина(X) :- Пол(X, мужской).
27
28. Программа «Дерево родственных отношений»
ИмеетРебенка(X) :- Родитель(X, _). % анонимная переменнаяОтпрыск(Y, X) :- Родитель(X, Y).
Мать(X, Y) :- Родитель(X, Y), Женщина(X).
Сестра(X, Y) :- Родитель(Z, X), Родитель(Z, Y), Женщина(X).
Goal
Сестра(энн, пат).
Ответ
yes.
Goal
Сестра(X, пат).
Ответ
X=энн, Х=пат. % упущение пат = сестра себе самой
28
29. Программа «Дерево родственных отношений»
Определим отношение Мать29
30. Программа «Дерево родственных отношений»
Определим отношение МатьМать(X, Y) :- Родитель(X, Y), Женщина(X).
Goal
Мать(X, боб).
Ответ
X=пам.
30
31. Программа «Дерево родственных отношений»
Определим отношение Сестра31
32. Программа «Дерево родственных отношений»
Определим отношение СестраСестра(X, Y) :- Родитель(Z, X), Родитель(Z, Y), Женщина(X).
Goal
Сестра(энн, пат).
Ответ
yes.
Goal
Сестра(X, пат).
Ответ
X=энн, Х=пат. % упущение пат = сестра себе самой
32
33. Программа «Дерево родственных отношений»
Определим отношение РазличныРазличны(X, Х) :- !, fail.
Различны(X, Y).
Сестра(X, Y) :- Родитель(Z, X), Родитель(Z, Y), Женщина(X),
Различны(X, Y).
Goal
Сестра(X, пат).
Ответ
X=энн
33
34. Поиск решения в Пролог-программе
В разделе Сlauses методом перебора сверху вниз производитсяпоиск факта или головы правила с предикатом того же типа, что и в цели.
При совпадении имен предикатов, количества и типов аргументов,
производится их сопоставление, называемое также унификацией.
Если аргумент в запросе является константой, а в факте тоже
константа с тем же значением, то сопоставление заканчивается успешно.
При сопоставлении переменной с константой, эта переменная
получает значение константы.
При сопоставлении переменной с переменной, у которой другое
имя, первая переменная получает ее имя. Далее производится
сопоставление следующего аргумента и т.д.
Если произошло успешное сопоставление всех аргументов, то
соответствующий предикат в цели получает значение истинности, а его
переменные получают значения соответствующих констант и становятся
связанными переменными.
Если ни одно из указанных условий унификации, хотя бы для
одного из аргументов, не выполнено, то сопоставления не произошло и
предикат в цели получает значение ложь. В этом случае продолжается
поиск и выбор для сопоставления следующих фактов.
34
35. Программа «Дерево родственных отношений»
Определим отношение Предок35
36. Программа «Дерево родственных отношений»
Определим отношение ПредокПредок(X, Y) :- Родитель(X, Y).
Предок(X, Y) :- Родитель(X, Z), Родитель(Z, Y).
…
36
37. Программа «Дерево родственных отношений»
Определим отношение ПредокПредок(X, Y) :- Родитель(X, Y).
Предок(X, Y) :- Родитель(X, Z), Предок(Z, Y).
37
38. Программа «Дерево родственных отношений»
Рассмотрим все шаги достижения целиGoal
Предок(том, пат).
38
39. Работа с арифметическими операциями
max(C1,C2,C1):-C1>C2, !.max(C1,C2,C2).
39
40. Метод повтopа по выбоpу пpогpаммиста
repeat.repeat:-repeat.
/* повторить */
40
41. Пример программы с использованием повтopа
domainsname = symbol
predicates
repeat
write_message
do_echo
check(name)
clauses
repeat.
repeat :- repeat.
write_message :- nl, write("Вводите названия животных."), nl,
write("Я повторю их."), nl,
write("Чтобы остановиться, введите stop."),nl,nl.
do_echo :- repeat, readln(N), /* ввод значения симв.переменной */
write(N),nl, check(N),!.
check(stop) :- nl, write(" Конец!").
check(_) :- fail.
goal
41
write_message, do_echo.
42. Применение рекурсии
predicateswrite_string
clauses
write_string:- write("Пусть всегда будет солнце!"),nl, write_string.
goal
write_string.
42
43. Применение рекурсии
<имя правила рекурсии>:<список предикатов для повторного выполнения>,<предикат с условием выхода>,
<список предикатов>,
<имя правила рекурсии>,
<список предикатов>.
43
44. Вычисление факториала при помощи простой рекурсии
predicatesfact(integer,real)
clauses
fact(0,1):-!.
fact(X,FactX):-Y=X-1, fact(Y,FactY), FactX=X*FactY.
goal
fact(5, X).
44
45. Вычисление факториала при помощи хвостовой рекурсии
predicatesfact(integer,real)
fact(integer,real,integer,real)
clauses
fact(N, FactN):- fact(N,FactN,0,1).
fact(N, FactN,N,FactN):- !.
fact(N, FactN,I,P):- NewI=I+1,NewP=P*NewI, fact(N,FactN,NewI,NewP).
goal
fact(5, X).
45
46. Работа со списками
Список - это упорядоченный набор объектов, следующих друг задругом. Составляющие списка внутренне связаны между собой, поэтому
с ними можно работать и как с группой (списком в целом), так и как с
индивидуальными объектами (элементами списка).
Список является набором объектов одного и того же типа.
Примеры списков :
[1,2,3,6,9,3,4]
[3.2,4.6,1.1,2.64,100.2]
["Вчера","Сегодня","Завтра"]
Список, не содержащий элементов, называется пустым или
нулевым списком и обозначается так: [ ].
Непустой список можно рассматривать как состоящий из двух
частей: первый элемент списка - его голова, и остальная часть списка хвост. Голова является элементом списка, хвост есть список сам по себе:
[Head|Tail].
Head является переменной для обозначения головы списка,
переменная Tail обозначает хвост списка.
Отличительной особенностью описания списка является
наличие звездочки (*) после имени списка элементов.
46
47. Работа со списками
/* Программа: П т и ц ы. Работа со списками. */domains
bird_name = symbol
bird_list = bird_name*
predicates
birds(bird_list)
clauses
birds(["ласточка","синица","чиж","воробей"]).
Выполним программу со следующими внешними запросами:
birds(All).
birds([_,_,_,B]).
birds([B1,B2,_,_]).
47
48. Работа со списками
Вывод элементов списка:print_list([ ]).
print_list([Head|Tail]) :- write(Head), nl, print_list(Tail).
Поиск элемента в списке:
find_it(Head,[Head|_]).
find_it(Head,[_|Tail]) :- find_it(Head,Tail).
48
49. Работа со списками
/* Программа: " Деление списка" */Domains
middle = integer
list
= integer*
Predicates
split(middle,list,list,list)
Clauses
split(Middle, [Head | Tail], [Head | L1], L2) :-Head <= Middle,
split(Middle,Tail,L1,L2).
split(Middle, [Head | Tail], L1, [Head | L2]) :split(Middle,Tail,L1,L2), Head > Middle.
split(_, [], [], []).
Goal
split(12,[96,32,8,16,55,12],L1,L2), write(“L1=”, L1, “, L2=”, L2).
49
50. Работа со списками
/* Программа: " Подсчет количества элементов списка". */domains
number =
integer
list
=
integer*
predicates
sum_list(list,number)
clauses
sum_list([ ], 0).
sum_list([H | T], Sum) :- sum_list(T, Sum1), Sum = 1 + Sum1.
50
51. Работа со списками
/* Программа: "Присоединение списка" */domains
n_list = integer *
predicates
append(n_list,n_list,n_list)
clauses
append([ ],L,L).
append([N|L1],L2,[N|L3]) :- append(L1,L2,L3).
goal
append([9,15,3,60,55],[15,2,21],L).
51
52. Работа со списками
/* Программа: Сортировка списка целых чисел в порядке возрастания. */domains
number =
integer
list
=
number*
predicates
sort(list,list)
insert(number,list,list)
order(number,number)
clauses
sort([ ],[ ]).
sort([X|Tail],Sorted_list) :- sort (Tail,Sorted_Tail),
insert(X,Sorted_Tail,Sorted_list).
insert(X,[Y|Sorted_list],[Y|Sorted_list1]) :- order(X,Y), !,
insert(X,Sorted_list,Sorted_list1).
insert(X,Sorted_list,[X|Sorted_list]).
order(X,Y) :- X>Y.
goal
sort([4,7,3,9],S).
52
53. Работа со списками
domainsn=integer
l=n*
predicates
conc(l,l,l)
mem(n,l)
mem1(n,l)
subl(l,l)
del(n,l,l)
del1(n,l,l)
ins(n,l,l)
clauses
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Конкатенация 2-х списков
conc([],L,L).
conc([H|T1],L1,[H|L]):-conc(T1,L1,L).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
ins(X,L,L1):-conc([X],L,L1).
53
54. Работа со списками
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Принадлежит ли элемент X списку L
% процедурная реализация
mem(X,[X|_]).
mem(X,[_|T]):-mem(X,T).
% декларативная реализация
mem1(X,L):-conc(_,[X|_],L).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Удаление элемента X из списка L
% процедурная реализация
del(_,[ ],[ ]).
del(X,[X|T],T):-!.
del(X,[H|L],[H|L1]):-del(X,L,L1).
% декларативная реализация
del1(X,L,L1):-conc(A,[X|B],L),conc(A,B,L1),!.
del1(_,L,L).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
54
55. Работа со списками
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Является ли L1 подсписком L
% декларативная реализация
subl([ ],_).
subl(L1,L):-conc(L2,_,L),conc(_,L1,L2).
55
56. Динамические базы данных
Динамические БД состоят из фактов, которые можно добавлять иудалять во время выполнения программы. Для хранения таких фактов в
программу вводится специальная секция database. Можно объявлять
предикаты динамической БД в секциях database программы и
использовать их таким же образом, как и предикаты, описанные в
секциях predicates.
Для добавления новых фактов в базу данных в Прологе
используются предикаты asserta и assertz, а предикаты retract и retractall
служат для удаления существующих фактов.
Можно изменить содержание БД сначала удалив факт, а потом
вставив новую версию этого факта (или другой факт). Предикат consult
считывает факты из файла и добавляет их к внутренней БД, а предикат
save сохраняет содержимое внутренней секции database в файле.
56
57. Динамические базы данных
Стандартные предикаты asserta, assertz, retract, retractall, consult,save могут иметь один или два агрумента.
Необязательный второй аргумент представляет собой имя БД.
По умолчанию ей присваивается стандартное имя dbasedom.
Предикат asserta вставляет новый факт в базу данных перед
имеющимися фактами для данного предиката, а assertz вставляет факты
после данного предиката.
asserta( <факт> )
- (i)
asserta( <факт>, dbaseName )
- (i,i)
assertz( <факт> )
- (i)
assertz( <факт>, dbaseName )
- (i,i)
Предикат retract удаляет первый факт в базе данных, который
совпадает с фактом <факт>. При поиске с возвратом предикат retract
возвращает альтернативные решения и удаляет все совпадающие
факты, пока они имеются. Предикат retractall удаляет из базы данных все
факты, совпадающие с образцом <факт>.
retract(<факт> [,databaseName])
- (i,i)
retractall(<факт> [,databaseName]) - (i,i)
57
58. Динамические базы данных
Предикат consult считывает из файла факты, описанные всекции database, и вставляет их в конец соответствующей БД.
consult( fileName )
- (i)
consult( fileName, databaseName ) - (i,i)
Файлы не должны содержать:
- прописных символов;
- пробелов, за исключением тех, которые содержатся внутри строк в
двойных кавычках;
- комментариев;
- пустых строк;
- символов без двойных кавычек.
Предикат save сохраняет факты из указанной базы данных в
файле.
save( fileName )
- (i)
save( fileName, databaseName ) - (i,i)
58
59. Пример программы с динамической базой данных
databasexm(integer)
domains
m, r = integer
predicates
rez(m, r)
print_rez
out(m)
clauses
rez(1,11).
rez(1,12).
rez(2,22).
rez(3,33).
rez(3,31).
rez(8,88).
rez(8,18).
rez(9,99).
print_rez:-readint(N),out(N).
out(N):-rez(X,Y),X<=N,not(xm(X)),asserta(xm(X)),write(X," ",Y),nl,fail.
goal
print_rez.
59
60. Принцип резолюций
Понятие логической программы рассматривается в контексте спонятием логического вывода.
Из совокупности логических предложений, представляющих
знание о задаче, выводится новое утверждение. Для придания
операционного характера логическим программам вводится понятие
процедурной интерпретации.
Толкование термина «логическая программа» основано на
интерпретации правила
P(t1,…,tn) :- P1(a11,…,am1), …, Pk(am1,…,amk)
как процедуры, сводящей решение задачи Р к решению подзадач Р1, …,
Рk.
Вопрос рассматривается как вызов процедуры – предикатный символ.
Аргументы предиката вопроса – это фактические параметры.
Аргументы предиката правила Р – это формальные параметры.
Вызов всей программы к исполнению основан на предположении, что
некоторая конъюнкция целей является логическим следствием
программы.
60
61. Принцип резолюций
Значением логической программы называется множествовыводимых из программы фактов, не содержащих переменных.
В логических программах используется простейшее правило
вывода, называемое принципом (правилом) резолюций.
Простейший случай правила – это
- Программа, не содержащая переменных.
- Вопрос, не содержащий переменных.
Условимся различать программу и задачу. Программа содержит
гипотезы: правила-аксиомы и факты. Задача – это вопрос.
В логической программе предложения–гипотезы – ресурсы, используемые
системой вывода для достижения целей. Цель – задача (теорема), которую
следует доказать от противного: доказательство успешно, если приходят к
противоречию.
Цель вывода – доказать, что из множества предложений S можно
вывести новое предложение: S |= s.
61
62. Принцип резолюций
Будем применять резолюцию к 3 типам предложений:• Отрицанию (A1, …, An).
• Факту А.
• Конъюнкции (правилу) А В1, …, Вm.
Для удобства вывода каждое предложение будем помечать,
например, Si – метка i-го предложения.
Введем резолюцию следующим образом.
S1:
(
A1, …, Ak-1, Ak, Ak+1,…, An).
S2:
Аk В1, …, Вm.
--------------------------------------------------S:
(
A1, …, Ak-1, В1, …, Вm, Ak+1,…, An),
где S1, S2 – родительские правила, S – резольвента.
Предложение S1 – отрицание целевого утверждения. Предложение
S2 извлекается из области знаний логической программы, в результате
правила резолюций получается резольвента S, которая представляет
собой отрицание некоторого предложения.
62
63. Принцип резолюций
Частный случай:S1:
(
A1, …, Ak-1, Ak, Ak+1,…, An).
S2:
Аk.
-----------------------------------------------S:
(
A1, …, Ak-1,
Ak+1,…, An).
Простейшие случаи резолютивного вывода:
а)
б)
S1:
A.
S2:
А
--------------------------S:
S1:
A.
S2:
А.
--------------------------S:
.
В.
В.
(пустое отрицание, противоречие)
63
64. Принцип резолюций
Пример. Построить последовательность резольвент для решения задачи:Получает ли Сидоров стипендию?
S1:
студент(петров).
S2:
студент(сидоров).
…
S3:
сессия-сдана(петров).
S4:
сессия-сдана(сидоров).
S5:
получает-стипендию(X) :- студент(Х), сессия-сдана(Х).
G:
получает-стипендию(сидоров)?
64
65. Принцип резолюций
Решение.Система вывода преобразует задачу в предложение:
G(S0): получает-стипендию(сидоров).
Теперь система ищет предикат получает-стипендию, выбирает
предложение S5, при этом Х примет значение {X:=сидоров}:
S5:
получает-стипендию(сидоров) :- студент(сидоров),
сессия-сдана(сидоров).
Получение первой резольвенты:
L1:
(студент(сидоров), сессия-сдана(сидоров)).
S2:
студент(сидоров).
-----------------------------------------L2:
сессия-сдана(сидоров).
S4:
сессия-сдана(сидоров).
----------------------------------------L3:
.
Последовательность предложений { S1, S2, …, Sk } – вывод задачи.
Вывод L1, L2, L3 решает задачу, т.к. в теории резолюций доказана
теорема, согласно которой:
S = { S1, S2, …, Sk } |= G <=> S, G |= .
65
66. Свойства резолюции
Свойство корректности:S, G |= =>
S |= G.
Свойство полноты:
S |= G
S, G |= .
=>
Эти свойства не обеспечивают неограниченность возможности
резолюции при доказательстве, поэтому основной проблемой, связанной
с формальной логической системой, является проблема общей
значимости. Проблема общей значимости связана с понятием
интерпретации предложений.
66
67. Проблема общей значимости
Пусть S – множество предложений, D – множество индивидуумовили область интерпретации. Предложения S интерпретируются как
высказывания об области D, если:
• Каждому индивидууму из D ставится в соответствие имя из S.
• Каждому функтору из S ставится в соответствие функция, определенная
на D.
• Каждому предикатному символу из S ставится в соответствие некоторое
отношение на D.
Т.о., если говорят, что предложение из S истинно или ложно
относительно выбранной интерпретации, то это означает, что истинно или
ложно соответствующее высказывание из области D.
Предложение программы называется общезначимым, если оно
выполняется во всех интерпретациях над произвольными областями D.
67
68. Проблема общей значимости
Проблема общей значимости частично разрешима для логики 1-гопорядка. Это значит, что не существует алгоритма, позволяющего для
произвольных S и D сделать вывод, справедливо ли отношение S |= G. Но
имеются алгоритмы, которые устанавливают справедливость этого
отношения (S |= G), если оно имеет место. Такие алгоритмы называются
частично разрешающими процедурами, и к ним относятся процедуры,
основанные на правиле резолюций. Т.о., если программа, не имеющая
опровержения, подается на вход частично разрешающей процедуры, то
вывод может оказаться бесконечным.
На практике незавершаемость разрешимой программы может быть
следствием выбора стратегии управления, реализованной в системе
вывода.
68
69. Правило вычисления и правило поиска
Согласно процедурной интерпретации, на каждом шаге выводапроисходит вход в вызывающую и вызываемую процедуры. Выход из
процедуры происходит, когда согласованы все вызовы из ее тела.
Система должна принять решение о выборе вызова, т.е. установить
правило вычислений.
Правило вычисления стандартно, если на каждом шаге выбирается
первый вызов.
Предложения программы могут содержать несколько процедур,
отвечающих выбранному вызову. Система должна установить правило
поиска процедуры.
Правило поиска стандартно, если процедура выбирается согласно
порядка следования в БЗ.
69
70. Стратегия управления
Стратегия управления стандартна, еслиправило вычисления и правило поиска стандартны.
70
71. Полное пространство вычислений
Теоретически программа может иметь вычисления:• Успешные (удачные) – заканчиваются противоречием.
• Неудачные – не хватает информации в БЗ.
• Незавершенные – неудачное использование предиката отсечения.
• Бесконечные – множество резольвент бесконечно.
Полным пространством вычислений называется множество всех
вычислений, которое можно получить при помощи операции вызова
процедуры, т.е. это перебор всех путей, которые могут иметь различные
исходы.
Размеры и структура пространства зависят от стратегии
управления. Наглядно пространство вычислений представляют в виде
дерева вычислений.
Корень дерева – исходное целевое утверждение.
Вершины – резольвенты.
71
72. Полное пространство вычислений
Пример. Построить полное пространство вычислений для задачи:получает-стипендию(сидоров)?
? получает-стипендию(сидоров)
|
| {Х:=сидоров}
|
? (студент(сидоров), сессия-сдана(сидоров)).
/\
/ \
сессия-сдана(сидоров) (студент(сидоров),
|
|
|
|
. (Да)
. (Да)
72
73. Подстановка
Подстановкой Θ (thita) называется множество присваиванийΘ = { Xi=ti | i=1 n }, где ti- термы-значения.
Каждой переменной присваивается не более 1 терма-значения.
Замечание. В процессе вывода терм-значение может быть
переменной величиной. X:=Y.
Существует соглашение: в качестве термов-значений принимать
переменные из родительского предложения (из отрицания).
Например, для
Si:
(P1(t),P2(t,X)).
Sj:
P2(Y,Z):-P3(Z)).
Θ = { Y:=t, Z:=X }.
73
74. Подстановочный пример
Пусть PΘ – результат применения подстановки Θ к Р.Р (рукописная русская Р) = РΘ называется подстановочным
примером.
Если Р = Р1Θ и Р = Р2Θ, то Р называется общим примером, а Θ –
унификатором.
Пример.
P(f(T),f(5),T) и P(X, f(Y), Y):
Θ = { X:=f(5), Y=5, T:=5 }, Р = P(f(5), f(5), 5).
74
75. Наиболее общий унификатор (НОУ)
В случае применения резолюции используют наиболее общийунификатор (НОУ=MGU). В системах резолютивного вывода НОУ строится
автоматически.
Пусть P(t1) – активизированный системный вызов,
P(t2) – выбранная процедура,
t1 = (t11,…,t1n) – кортеж фактических параметров,
t2 = (t21,…,t2n) – кортеж формальных параметров,
Θ – унификатор.
При использовании системой алгоритма унификации Робинсона
данными для алгоритма являются списки:
l1- список фактических параметров t1,
l2 список формальных параметров t2,
Θ – пустой список.
В процессе доказательства Θ наполняется присваиваниями вида
{ t2i:=t1i }.
Результатом алгоритма является НОУ – заключительное состояние
списка Θ.
75
76. Алгоритм унификации Робинсона
Алгоритм Робинсона циклический. Рассмотрим описание i- го шага.1. Если t1i – переменная, не входящая в t2i, то Θ = Θ { t1i:=t2i }.
2. Если t2i – переменная, не входящая в t1i, то Θ = Θ { t2i:=t1i }.
3. Если t1i = (a1,…,am) и t2i = (b1,…,bm), то формируются множества
{ai:=bi} или {bi:=ai} и присоединяются к Θ; L1 ={ai}, L2 ={bi}
4. Если t1i, t2i – одинаковые константы или одинаковые
переменные,
то Θ, L1, L2 не обновляются и выполняется
переход к шагу i+1.
5. В остальных случаях – работа алгоритма заканчивается.
76
77. Принцип резолюции для общего случая
S1:S2:
(
A1, …, Ak-1, Ak, Ak+1,…, An).
Аk (консеквент) В1, …, Вm (антеценденты).
Допустим, предложения S1, S2 содержат переменные, тогда с
учетом спецификаций для выполнения шага вывода требуется:
1. Заменить общие переменные S1, S2 на новые (обычно
переименовываются в S2).
2. Выбрать в S1 предикат, у которого предикатный символ
совпадает с консеквентом в S2. Если такого предиката в S1 нет, то
шаг вывода невозможен.
3. Найти НОУ Θ для Ak из S1 и S2. Если Θ, то шаг вывода
невозможен.
4. Построить резольвенту.
5. Применить Θ к резольвенте.
77
78. Разрешимость логических программ
Разрешимость ЛП и значение ЛП – тесно связанные понятия.Пусть Р – множество процедур,
G- задача: ?g1(t), …, gn(t).
Тогда парой (P, G) обозначим программу.
Определение. (P, G) разрешима <=> ( Θ) (P |= g1(tΘ), …, gn(tΘ)).
Разрешимость пары (P, G) можно установить либо исполнением
программы (P,G), либо анализом спецификаций этой программы.
78
79. Спецификация программ
Определение. Спецификация программы (P, G) – это любоемножество определений, которое точно задает каждое отношение
программы.
Пример. Специфицируем отношение подмножества (X, Y), т.е. X –
подмножество Y.
79
80. Спецификация программ
Определение. Спецификация программы (P, G) – это любоемножество определений, которое точно задает каждое отношение
программы.
Пример. Специфицируем отношение подмножества (X, Y), т.е. X –
подмножество Y.
S1:
подмножество(X, Y) <=> ( U) (U Y если U X).
80
81. Верификация программ
Обозначим S = { S1, …, Sn}, P = { P1, …, Pm, G}.Доказательство корректности P относительно S и является
проверкой правильности программы (верификацией).
Верификация сводится к доказательству того,
что вычисленные решения являются правильными,
все правильные решения получены данными программы.
Полагаем:
что G представляет только одну цель, только один вызов,
что S непротиворечиво, написано на языке логики предикатов 1
порядка.
81
82. Специфицируемость и вычисляемость
Пустьgs – основное специфицируемое отношение,
Rs – множество решений tΘ, которые удовлетворяют соотношению
S |= gs(tΘ). Это интервал целевого утверждения относительно S:
Rs = { tΘ | S |= gs(tΘ) }
(если t содержит термы-переменные, то gs(t) выделит некоторую
часть отношения gs).
Определение. Решение tΘ называется специфицируемым,
если tΘ Rs.
Верификация программы (P, G) должна выяснить, является ли tΘ
вычисляемым.
Введем интервал (вычисляемое отношение)
R = { tΘ | P |= gs(tΘ) } для определения таких решений, которые
порождаются tΘ.
Определение. tΘ – вычисляемое решение задачи G, если tΘ R.
82
83. Специфицируемость и вычисляемость
Замечания.1. Если кортеж tΘ не содержит переменных, то tΘ R.
2. Если интервал Rs пуст, то программа не должна иметь решения.
83
84. Полная правильность программ
Определение. Если программа (P, G) полностью правильная, то:1. Вычисляемое программой решение правильно относительно S.
(частичная правильность)
2. Каждое решение, приписываемое спецификацией S предложению
G должно быть вычисляемым программой (P, G). (полнота)
84
85. Частичная правильность программ
Определение. Программа частично правильна <==> выполняется 1из условий:
1. ( Θ) ( (tΘ R) => (tΘ Rs)).
2. R Rs.
3. ( Θ) ( (P |= gs(tΘ)) => (S |= gs(tΘ)) ).
Т.е. совсем не требуется, чтобы tΘ вычислялось, а требуется,
чтобы вычисляемое решение было специфицируемым.
Замечания.
1. Неразрешимые программы являются частично правильными.
2. Программа, не вычисляющая никакого решения, не может
вычислить и правильного решения.
85
86. Полнота программ
Определение. Программа (P, G) полна для G относительно S <==>выполняется 1 из условий:
1. ( Θ) ( (tΘ Rs) => (tΘ R)).
2. Rs R.
3. ( Θ) ( (S |= gs(tΘ)) => (P |= gs(tΘ)) ).
Т.е. процедур из P достаточно, чтобы вычислить все решения из
Rs.
Некоторые множества Р являются полными вне зависимости от G.
Их называют полными относительно S.
Определение. P полно относительно S <=>
( T) ( (S |= gs(T)) => (P |= gs(T)) )
где Т не обязательно имеет вид tΘ.
86
87. Полная правильность программ относительно спецификации
Определение. Программа (P, G) является полностью правильнойотносительно S <==> выполняется 1 из условий:
1. ( Θ) ( (tΘ Rs) <=> (tΘ R)).
2. Rs = R.
3. ( Θ) ( (S |= gs(tΘ)) <=> (P |= gs(tΘ)) ).
Т.е. вычисляемое и специфицируемое решения совпадают.
Замечание. Если (P, G) не является полностью правильной, то:
1. Либо она вычисляет некоторое неправильное решение, т.к. Р
неправильно описывает проблемную область.
2. Либо не может вычислить некоторое правильное решение, т.к. не
хватает информации о проблемной области.
87
88. Проверка правильности программ. Пример
Задача. Написать БД, позволяющую осуществить поиск ответов навопросы:
1. Является ли человек Х студентом?
2. Человек Х успевает?
3. Получает ли человек Х стипендию?
88
89. Проверка правильности программ. Пример
Решение.Возможные спецификации:
S1:
студент(Х) <=> (X студ).
S2:
успевающий(Х) <=> (X усп).
S3:
получает-стипендию(Х) <=> (X студ, X усп).
S4:
?студент(x) <=> (x студ) => T1=true.
S5:
?успевающий(x) <=> (x усп) => T2=true.
S6:
?получает-стипендию(x) <=> (T1=true, T2=true) => T3=true.
S7:
студ
= { иванов, петров, сидоров }.
S8:
усп
= { иванов, петров, сидоров }.
Rs = { X=иванов, X=петров, X=сидоров }.
89
90. Проверка правильности программ. Пример
Решение.Программа (P, G):
P1:
студент(иванов).
P2:
студент(петров).
P3:
студент(сидоров).
P4:
успевающий(петров).
P5:
успевающий(сидоров).
P6:
получает-стипендию(Х) :- студент(Х), успевающий(Х).
R = { X=петров, X=сидоров }.
Вывод программа – частично правильна.
Чтобы сделать ее полностью правильной, необходимо добавить
предложение
P7:
успевающий(иванов).
Замечание. Сформулированные критерии называются
минимальными (правильность зависит от G).
90
91. Проверка правильности программ. Пример
Пример. Программа становится неправильной лишь при замене G(P сохраняется).
Р1: сумма(Т, 0, Т).
Р2: сумма(Y, 2, 3).
Р3: сумма(Т, 1, Z) :- сумма(Т, 0, Y), сумма(Y,2, Z).
G: ? сумма(2, 1, Х).
91
92. Проверка правильности программ. Пример
1. Cпецификации:S1: сумма(T1, T2, T3) <=> T3=T1+T2.
S2: ? сумма(2, 1, X) <=> (X=2+1, X=3).
Rs = { X=3 }.
92
93. Проверка правильности программ. Пример
2. Вычислим решение, составляющее R с помощью стандартнойстратегии управления:
S0:
сумма(2, 1, Х).
Р1:
сумма(Т, 0, Т).
----------------------------------------Θ = .
S0:
сумма(2, 1, Х).
Р2:
сумма(Y, 2, 3).
----------------------------------------Θ = .
S0:
сумма(2, 1, Х).
Р3:
сумма(Т, 1, Z).
----------------------------------------Θ = { T:=2, Z:=X }.
S1:
сумма(2, 0, Y).
Р1:
сумма(2, 0, 2).
----------------------------------------Θ = { T:=2, Z:=X, Y:=2 }.
S2:
сумма(2, 2, X).
Р2:
сумма(2, 2, 3).
----------------------------------------S3:
.
R = { X=3 }.
93
94. Проверка правильности программ. Пример
Изменим целевое утверждение.G: ? сумма(1, 1, Х).
S2': сумма(1, 1, X) <=> (X=1+1, X=2).
Программа вычисляет решение R’s = { X=2 }
Rs <> R’s.
Поэтому программа не является правильной для данного G.
Объяснение. Использованные критерии правильности являются
необходимыми условиями. Они не накладывают ограничений на
отдельные процедуры. Процедура Р2 бессмысленна (она не
верна Y<>1).
По этой причине на практике пользуются достаточными
условиями правильности программ.
94
95. Достаточные условия правильности программ
Теорема 1. Если S |= P, то (P, G) частично правильная относительно S.□:
tΘ – произвольно вычисляемое решение для целей. Поэтому
S |= P
} P |= gs(tΘ) => S |= gs(tΘ) (в силу транзитивности).
tΘ
Таким образом, выполняется ( Θ) ( (P |= gs(tΘ)) => (S |= gs(tΘ)) ).
Следовательно, по определению, (P, G) частично правильная.
■.
Теорема 2. Если Р полно относительно S, то Р полно для цели G относительно S.
□:
В силу того, что Р полно относительно S:
( t) ( (S |= gs(t)) => (P |= gs(t)) )
в силу произвольности t следует, что какую бы подстановку мы не взяли, можно
работать с решением:
( Θ) ( (S |= gs(tΘ)) => (P |= gs(tΘ)) ).
Следовательно, Р полно для G относительно S по определению.
■.
Теорема 3. Если S |= P и Р полно относительно S то (P, G) полностью правильная
относительно S.
□:
Т.к. S |= P то (P, G) частично правильная относительно S. (теорема 1)
Т.к. Р полно относительно S то (Р, G) полна для цели G относительно S. (теорема 2)■.
95
96. Достаточные условия правильности программ
Замечания.1.
Условие S |= P не зависит от G. Смысл условия: Р полностью
описывает S. На практике неполнота Р может быть оправдана
необходимостью вычислений неполного пространства решений
программы (Р, G) или негибкостью языка представления процедур Р.
2.
Если (Р, G) полна относительно S, то из ( Θ) (S |= gs(tΘ)) следует,
что (Р, G) разрешима. Обратное неверно.
3.
Если (Р, G) частично правильна, ( Θ) (S |= gs(tΘ)), то (Р, G) –
неразрешима. Обратное неверно.
96
97. Правильность исполнения логических программ
Пусть: С - стратегия управления, Г(гамма) - вычисление.Тогда (P(множество процедур), G(цель), C(стратегия управления)) – это есть
исполнение.
Определение. Г производимо из (P, G) при управлении С <=> тройка (P, G, C)
порождает каждое целевое утверждение из Г за конечное число шагов.
Определение. Вычисляемое решение (tΘ) производимо из (P, G) при
управлении С <=> (tΘ) вычислимо за конечное время: (P |=с gs(tΘ)).
Замечание. Не каждая производимое вычисление Г дает производимое
решение.
97
98. Правильность исполнения логических программ
Пример Грина. Исполнить программу.P1:
g(Y):- p(Y), q(Y).
P2:
p(a).
P3:
q(a).
P4:
q(f(x)):-q(f(f(x))).
G:
?g(Y).
Стратегия C1 – стандартная. (P, G, C1) порождает вычисление Г1:
?g(Y).
?p(Y), q(Y).
?q(a).
? решение Y:=a
Г1 – конечное, производимое, успешное вычисление
Решение вычисляемо, т.к. P |= g(a). Решение производимо, т.к. получается за
конечное число шагов исполнения программы.
98
99. Правильность исполнения логических программ
Изменим P1P1:
g(Y):- q(Y), p(Y).
Стратегия C2 – стандартная стратегия управления
(P, G, C2) порождает вычисление Г2:
?g(Y).
?q(Y), p(Y).
?p(a).
? решение Y:=a
Стратегия C3 – нестандартная стратегия управления
(P, G, C3) порождает вычисление Г3:
?g(Y).
?q(Y), p(Y).
?q(f(f(X))), p(f(X)).
?q(f(f(f(X)))), p(f(f(X))).
...
99
100. Правильность исполнения логических программ
Вычисления Г1, Г2, Г3 – производимы.Г1, Г2 порождают производимое решение Y=a.
Г3 – бесконечно.
Если бы первоначально была выбрана стратегия 3, то логически полностью
правильная программа (P, G) не смогла бы породить решения.
Пример Грина показывает, почему при исследовании разрешимости
программы недостаточно требовать ее исполнения.
Теоретические исследования правильности исполнения программ используют
понятия частичной правильности и полноты (P, G, C) относительно S.
Г3 можно рассматривать как процесс синтеза программы, допускающий
воздействие f на объект X (данные).
Т.о. Г3 порождает зацикленную программу.
100
101. Правильность исполнения логических программ
Определение. (P, G, C) частично правильно относительно S<=> ( Θ) ((P |=c gs(tΘ)) => (S |= gs(tΘ))производимость специфицируемость
Определение. (P, G, C) полно относительно S <=> ( Θ) ( (S |= gs(tΘ)) => (P |=с gs(tΘ)) )
(tΘ производимо из Р с помощью С).
Определение. (P, G, C) полностью правильно относительно S <=> ( Θ) ( (S |= gs(tΘ)) <=> (P |=с gs(tΘ)) )
Теорема 4. Достаточное условие правильности (P, G, C).
Если (P, G) частично правильна относительно S то (P, G, C) частично правильно относительно S.
□:
Т.к. (P, G) частично правильная относительно S, то по определению ( Θ) ( (P |= gs(tΘ)) => (S |= gs(tΘ)) ).
Стратегия C основана на резолюции, система вывода корректная => производимое решение является вычисляемым, т.е. ( Θ) ( (P |=c
gs(tΘ)) => (P |= gs(tΘ)) ).
В силу транзитивности получаем ( Θ) ( (P |=с gs(tΘ)) => (S |= gs(tΘ)) ).■.
Теорема 5. Если (P, G) полна относительно S, (P, G) определяет конечное пространство вычислений,
исчерпывающая,
То (P, G, C) полно относительно S.
□:
стратегия
С
Т.к. (P, G) полна относительно S, то по определению ( Θ) ( (S |= gs(tΘ)) => (P|= gs(tΘ))).
Т.к. пространство вычислений конечно, Стратегия исследует все вычисления
=> все вычисляемые решения будут производимыми
т.е. ( Θ) ( (P |= gs(tΘ)) => (P |=с gs(tΘ)) ).
В силу транзитивности получаем
( Θ) ( (S |= gs(tΘ)) => (P |=с gs(tΘ)) ).■.
101
–
102. Правильность исполнения логических программ
Теорема 6. Если (P, G) полностью правильна относительно S, (P, G) определяет конечное пространствовычислений, стратегия С – обеспечивает исчерпывающее управление,
То (P, G, C) полностью правильно относительно S.
Комментарий. Т.к. мало формальных представлений сформулированных условий, на практике удобнее пользоваться
теоремой 7.
Теорема 7. Если S |= Р, Р полностью правильно относительно S,
(P,G) определяет конечное пространство вычислений, С – исчерпывающее управление
То (P, G, C) полностью правильно относительно S.
102
103. Удовлетворение ограничений и логическое программирование
CLP – Constraint Logic Programming(Логическое программирование в ограничениях)
Дано:
1) множество переменных;
2) области определения, из которых могут выбираться значения
переменных;
3) ограничения, которым должны удовлетворять переменные.
Найти:
такие значения, присваиваемые переменным, которые удовлетворяют
всем заданным ограничениям.
Примеры задач: задачи планирования, снабжения и управления ресурсами
на производстве, на транспорте и в складском хозяйстве.
Для решения этих задач необходимо распределять ресурсы по процессам,
например, автобусы по маршрутам; солдат по постам; экипажи по
самолетам; бригады по поездам; врачей и медсестер по дежурствам и
сменам и т.д.
103
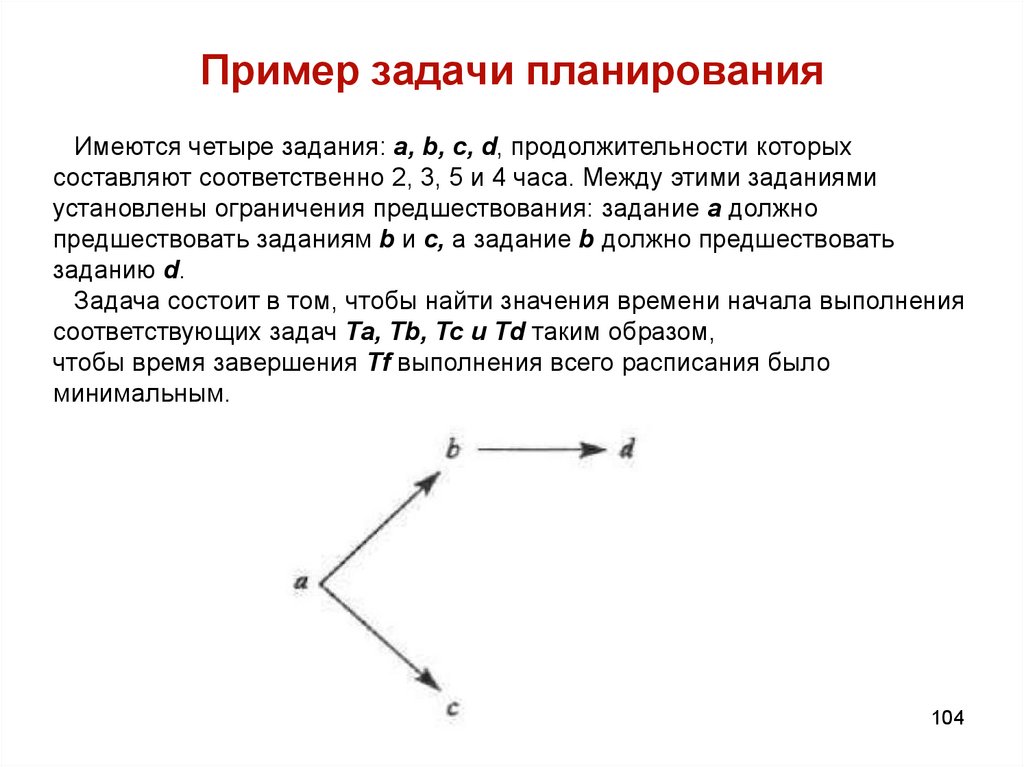
104. Пример задачи планирования
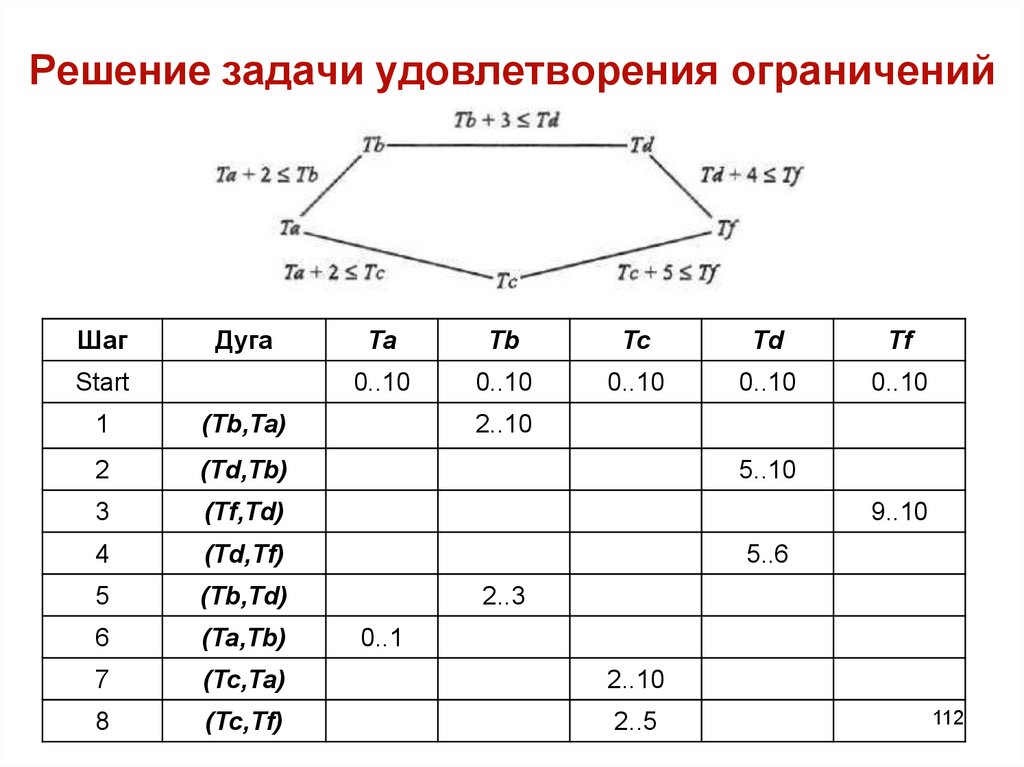
Имеются четыре задания: a, b, c, d, продолжительности которыхсоставляют соответственно 2, 3, 5 и 4 часа. Между этими заданиями
установлены ограничения предшествования: задание a должно
предшествовать заданиям b и c, а задание b должно предшествовать
заданию d.
Задача состоит в том, чтобы найти значения времени начала выполнения
соответствующих задач Та, Тb, Тс и Td таким образом,
чтобы время завершения Tf выполнения всего расписания было
минимальным.
104
105. Пример задачи планирования
Переменные: Та, Тb, Тс, Td , Tf.Области определения: все переменные — неотрицательные
действительные числа.
Ограничения:
Ta + 2 ≤ Tb. Задача а, на выполнение которой требуется 2 часа,
предшествует b;
Та + 2 ≤ Тс Задача а предшествует задаче с;
Тb + 3 ≤ Td. Задача b предшествует задаче d;
Тс + 5 ≤ Tf. Задача с завершается к моменту времени Tf;
Td + 4 < Tf. Задача d завершается к моменту времени Tf.
Критерий: минимизация значения Tf.
Задача удовлетворения ограничений имеет множество решений, причем все
они позволяют обеспечить минимальное время завершения.
Это множество решений можно определить следующим образом:
Та = 0
Тb = 2
2 ≤ Тc ≤ 4
Тd = 5
105
Тf = 9
106. Решение задачи удовлетворения ограничений
Условия задач удовлетворения ограничений часто изображаются в видеграфов, называемых сетями ограничений.
Узлы в графе – переменные, а дуги – ограничения.
Для каждого бинарного ограничения p(X,Y) между переменными X и Y в
этом ориентированном графе имеются две дуги: (X,Y) и (Y,X).
Для поиска решения задачи удовлетворения ограничений могут
использоваться различные алгоритмы обеспечения совместимости. Эти
алгоритмы лучше всего рассматривать как действующие в сетях
ограничений. Они проверяют совместимость областей определения
переменных с ограничениями.
Замечание. В общем случае ограничения могут связывать между собой
любое количество переменных (иметь любую арность).
106
107. Решение задачи удовлетворения ограничений
Рассмотрим переменные X и Y, которые имеют области определения Dx и Dy.Предположим, что между переменными X и Y задано бинарное ограничение
p(X,Y).
Дуга (X,Y) называется совместимой с определяемым ограничением, или
просто совместимой, если для каждого значения X в области определения
Dx существует некоторое значение для Y в области определения Dy,
удовлетворяющее ограничению р(X, Y).
Если (X, Y) не является совместимой, то все значения в области Dx, для
которых отсутствует соответствующее значение в области Dy, могут быть
удалены из Dx.
В результате дуга (X, Y) становится совместимой.
107
108. Решение задачи удовлетворения ограничений
Пример. Рассмотрим переменные X и Y, областями определения которыхявляются множества всех целых чисел от 0 до 10:
Dx = 0 . . 10 , Dy = 0 . . 10
Допустим, задано ограничение p(X,Y): X + 4 < Y.
В таком случае дуга (X,Y) перестает быть совместимой, т.к. для X = 7 в
области Dy нет значения Y, удовлетворяющего условию p(X,Y).
Для того чтобы дуга (X,Y) стала совместимой, область определения Dx
необходимо сократить до Dx = 0..6.
Аналогичным образом, дугу (Y,X) можно сделать совместимой, сократив Dy
таким образом: Dy = 4..10.
Но в результате такого сокращения областей Dx и Dу мы не теряем ни одного
решения этой задачи удовлетворения ограничений, поскольку отброшенные
значения, безусловно, не должны были войти в состав какого-либо решения.
108
109. Решение задачи удовлетворения ограничений
После сокращения области Dx могут стать несовместимыми некоторыедругие дуги.
Например, для дуги, заданной как (Z,X), могут существовать такие значения
Z, для которых после сокращения Dx больше не будет ни одного
соответствующего значения в области Dx. После этого, в свою очередь,
можно сделать дугу (Z,X) совместимой, уменьшив соответствующим образом
область Dz.
Эффект подобного действия может в течение определенного времени
распространяться по всей сети, возможно, циклически, до тех пор, пока все
дуги не станут совместимыми или некоторая область определения не станет
пустой. В последнем случае, безусловно, ограничения не могут быть
удовлетворены. А в случае, если все дуги являются совместимыми, могут
возникать еще две ситуации:
1. Каждая область определения включает единственное значение; это
означает, что данная задача удовлетворения ограничений имеет
единственное решение.
2. Все области определения непусты, и по меньшей мере одна область
определения содержит несколько значений.
109
110. Решение задачи удовлетворения ограничений
Во второй ситуации, которая относится к тому случаю, когда все дугиявляются совместимыми, нет никакой гарантии, что все возможные сочетания
значений из областей определения являются решениями задачи
удовлетворения ограничений.
Может даже оказаться, что фактически ни одно сочетание значений не
удовлетворяет всем ограничениям.
Поэтому для поиска решения необходимо выполнить комбинаторный поиск
по сокращенным областям определения.
110
111. Варианты поиска удовлетворения ограничений
1. Выбрать какую-то из многозначных областей определения и попытатьсяпоочередно присвоить ее значения соответствующей переменной.
Присваивание конкретного значения переменной равносильно сокращению
области определения переменной, и такая операция может снова вызвать
появление несовместимых дуг. Таким образом, алгоритм обеспечения
совместимости может быть применен снова для дальнейшего сокращения
областей определения переменных и т.д. Если области определения
являются конечными, то такой способ действий может в конечном итоге
привести к получению либо какой-либо пустой области, либо
всех однозначных областей определения. Такой поиск может осуществляться
по-разному, а не обязательно с помощью выбора одного значения из
некоторой области.
2. Выбор области, состоящей из нескольких значений и разделения ее на два
подмножества приблизительно одинаковых размеров. После этого алгоритм
выбора отдельного значения применяется к обоим подмножествам.
111
112. Решение задачи удовлетворения ограничений
ШагДуга
Start
Ta
Tb
Tc
Td
Tf
0..10
0..10
0..10
0..10
0..10
1
(Tb,Ta)
2..10
2
(Td,Tb)
3
(Tf,Td)
4
(Td,Tf)
5
(Tb,Td)
6
(Ta,Tb)
7
(Tc,Ta)
2..10
8
(Tc,Tf)
2..5
5..10
9..10
5..6
2..3
0..1
112
113. Метаинтерпретатор Пролога (Пролог на Прологе)
prove(true) :- !.prove(','(A,B)):-prove(A),prove(B).
prove(G):-clause(G,Body),prove(Body).
parent(vasya,petya).
parent(anna,petya).
…
brother(X,Y) :parent(A,X), parent(A,Y), man(X).
?- prove(brother(X,Y)).
113
114. Индуктивное логическое программирование (ILP)
ILP (Inductive Logic Programming) - раздел машинного обучения, которыйиспользует логическое программирование как форму представления примеров,
фоновых знаний и гипотез.
Получив описания уже известных фоновых знаний и набор примеров,
представленных как логическая база фактов, система ILP может породить
логическую программу в форме гипотез, объясняющую все положительные
примеры и ни одного отрицательного.
Фоновые знания – знания, известные ученику до начала обучения.
Схема:
положительные примеры + отрицательные примеры + фоновые знания => гипотезы
Термин «индуктивное логическое программирование» был впервые
использован в статье Стивена Магглтона (Stephen Muggleton) в 1991 году.
Термин «индуктивное» здесь употребляется в философском (предложение
теории для объяснения наблюдаемых фактов), а не в математическом
114
(доказательство свойства членов множества) смысле.
115. Задача ILP
ILP – один из подходов к машинному обучению.Результат обучения – формула логики предикатов, обычно программа Prolog.
При таком подходе машинное обучение - это своего рода автоматическое
программирование, когда разработчик не занимается написанием программ.
Вместо этого он показывает на примерах, для выполнения каких действий
предназначена создаваемая программа.
«+»-примеры – указывают, что должна делать программа.
«-»-примеры – указывают, что эта программа не должна делать.
Кроме этого пользователь задает фоновые предикаты, которые могут
использоваться при написании новой программы.
115
116. Пример задачи ILP
Предположим, что имеются предикаты:parent(X, Y)
male(X)
female(X)
Необходимо найти определение нового предиката
has_daughter(X)
Даны «+»-примеры:
has_daughter(tom)
has_daughter(bob)
Даны «-»-примеры:
has_daughter(pam)
has_daughter(jim)
Задача – найти определение предиката has_daughter(X) в терминах предикатов
parent, male и female таким образом, чтобы он принимал истинное значение для
всех «+»-примеров и ложное значение для всех «-»-примеров.
116
117. Задача ILP
Приведенный пример демонстрирует типичное отличие такого реляционного(основанного на отношениях) обучения от обучения на основе атрибутов и
значений.
Свойство has_daughter объекта X определено не только в терминах атрибутов
X. Вместо этого для определения наличия у объекта X свойства
has_daughter рассматривается другой объект, Y, связанный с X, и проверяются
свойства объекта Y.
117
118. Терминология ILP
Предикат, который должен быть получен в результате обучения, has_daughter,называется целевым предикатом.
Заданные предикаты parent, male и female называются фоновыми знаниями
(Background Knowledge — ВК), или фоновыми предикатами. Это — знания,
известные ученику до начала обучения.
Фоновые предикаты фактически определяют язык, на котором ученик может
выражать гипотезы, относящиеся к целевому предикату.
118
119. Задача ILP
Дано:1. множество положительных примеров Е+ и множество отрицательных
примеров Е-;
2. фоновые знания ВК, заданные как множество логических формул, такие, что
примеры Е+ невозможно вывести логически из ВК.
Найти:
гипотезу Н, заданную как множество логических формул, такую, что
1. все положительные примеры в Е+ можно вывести логически из ВК и Н;
2, ни одного отрицательного примера в Е- нельзя вывести логически из ВК и Н.
119
120. Задача ILP
Дано:1. множество положительных примеров Е+ и множество отрицательных
примеров Е-;
2. фоновые знания ВК, заданные как множество логических формул, такие, что
примеры Е+ невозможно вывести логически из ВК.
Найти:
гипотезу Н, заданную как множество логических формул, такую, что
1. все положительные примеры в Е+ можно вывести логически из ВК и Н;
2, ни одного отрицательного примера в Е- нельзя вывести логически из ВК и Н.
Н вместе с BК должны охватывать все положительные примеры и не должны
охватывать ни одного из отрицательных примеров. Подобная гипотеза H
называется полной (охватывающей все положительные примеры) и
достоверной (совместимой только с положительными примерами, т.е. не
охватывающей ни одного отрицательного примера).
120
121. Задача ILP
Обычно ВК и Н представляют собой множества предложений Prolog-программы.Поэтому с точки зрения автоматического программирования на языке Prolog
приведенная выше формулировка задачи обучения соответствует следующей.
Предположим, что целевым предикатом является р (X) и кроме
прочих примеров имеются некоторые положительный пример р(а) и
отрицательный пример р(b).
Возможный диалог с программой ВК может состоять в следующем:
? р(а) . % Положительный пример
nо % Не может быть выведен логически из ВК
? p(b) . % Отрицательный пример
nо % Не может быть выведен логически из ВК
Теперь предположим, что вызвана на выполнение система ILP, которая
автоматически осуществляет логический вывод дополнительного множества
предложений Н и добавляет их к программе BK.
121
122. Задача ILP
После этого возможный диалог с расширенной таким образом программой,состоящей из предложений ВК и Н, может представлять собой следующее:
? р(а). % Положительный призер
yes % Может быть выведен логически из BК и Н
? р(b). % Отрицательный пример
nо % Не может быть выведен логически из ВК и Н
Широко известные задачи в области ILP: автоматическое формирование
программ Prolog для конкатенации или сортировки списков. Такие программы
создаются на основании положительных примеров того, как должна
осуществляться конкатенация или сортировка списков, а также отрицательных
примеров того, как эти действия не должны выполняться.
122
123. Определение задачи изучения предиката has_daughter
% Изучение предиката по фактам, определяющим семейные отношения% Фоновые знания
backliteral( parent(X,Y), [X,Y]). % Фоновый литерал с переменными [X,Y]
backliteral(male(X), [X]).
% 2-й аргумент – список переменных
backliteral( female(X), [X]).
prolog_predicate( parent(_,_)). % Цель parent(_,_) выполняется
% непосредственно интерпретатором Prolog
prolog_predicate( male(_)).
prolog_predicate( female(_)).
parent( pam, bob).
parent( torn, bob).
parent( torn, liz).
parent( bob, ann).
parent( bob, pat) .
parent( pat, jim).
parent( pat, eve).
123
124. Определение задачи изучения предиката has_daughter
female( pam).female( liz).
female( ann).
female( pat).
female( eve).
male( tom).
male( bob).
male( jim).
% Положительные примеры
ex( has_daughter(tom)). % Том имеет дочь
ex( has_daughter(bob)).
ex( has_daughter(pat)).
% Отрицательные примеры
nex( has_daughter(pam)). % Пэм не имеет дочери
nex( has_daughter(jim)).
start_hyp( [ [has_daughter(X)] / [X] ] ). % Начальная гипотеза
124
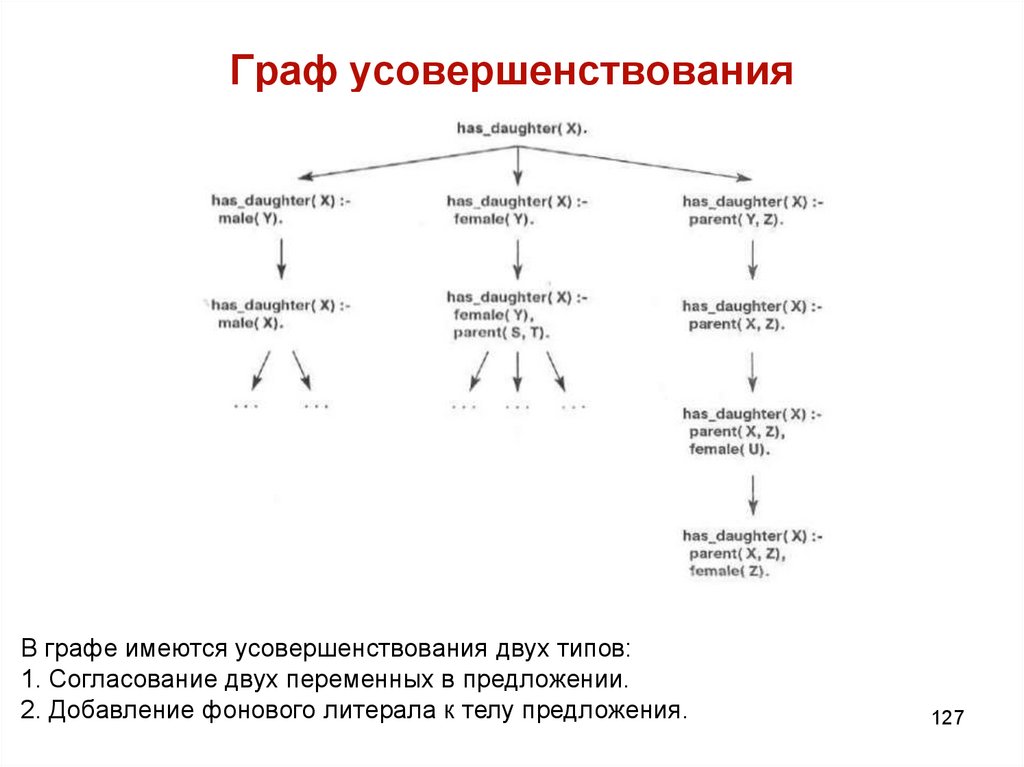
125. Граф усовершенствования
Можно начать с некоторой слишком общей гипотезы, которая является полной(охватывает все положительные примеры), но несовместимой (не охватывает
лишь положительные примеры, т.е. охватывает также отрицательные примеры).
Подобная гипотеза должна быть усовершенствована таким образом,
чтобы она сохранила свою полноту и стала совместимой. Этого можно достичь
путем поиска в пространстве возможных гипотез и их усовершенствований. При
каждом усовершенствовании берется гипотеза H1 и вырабатывается более
конкретная гипотеза Н2 такая, что H2 охватывает подмножество случаев,
охватываемых гипотезой H1.
Подобное пространство гипотез и их усовершенствований называется графом
усовершенствования.
Узлы в графе - гипотезы, а дуги между гипотезами - усовершенствования.
Между гипотезами H1 и Н2 имеется ориентированная дуга, если Н2 является
усовершенствованием H1.
125
126. Граф усовершенствования
После определения графа усовершенствования задача обучения сводится кпоиску в этом графе.
Начальный узел поиска - некоторая слишком общая гипотеза.
Целевой узел поиска - совместимая и полная гипотеза.
В примере достаточно, чтобы все гипотезы представляли собой отдельные
предложения, но в общем гипотезы могут состоять из нескольких предложений.
Для реализации описанного подхода необходимо разработать два компонента.
1. Оператор усовершенствования, который будет вырабатывать
усовершенствования гипотез (такой оператор определяет граф
усовершенствования).
2. Процедура поиска для выполнения поиска.
126
127. Граф усовершенствования
В графе имеются усовершенствования двух типов:1. Согласование двух переменных в предложении.
2. Добавление фонового литерала к телу предложения.
127
128. Граф усовершенствования
Пример усовершенствования 1 типа:has_daughter(X) :- patent(Y, Z).
Это предложение путем усовершенствования преобразуется в предложение
has_daughter(X) :- parent(X, Z).
в котором выполнено согласование X=Y.
Примером усовершенствования 2 типа:
has_daughter(X).
путем усовершенствования преобразуется в следующее предложение:
has_daughter(X) :- parent(Y, Z).
128
129. Граф усовершенствования
Особенности усовершенствований1. Каждое усовершенствование представляет собой уточнение. Преемник
любой гипотезы в графе усовершенствования охватывает лишь некоторое
подмножество тех случаев, которые охвачены предшественником этой гипотезы.
Поэтому в процессе поиска достаточно рассматривать только полные гипотезы
(которые охватывают все положительные примеры). Неполная гипотеза в
процессе усовершенствования не может стать полной.
2. Оператор усовершенствования должен осуществлять достаточно "малые"
этапы усовершенствования. В противном случае оператор усовершенствования
может не позволить выработать целевую гипотезу. Оператор, допускающий
слишком крупные этапы усовершенствования, может перейти от полной и
несовместимой гипотезы прямо к неполной и совместимой, минуя находящуюся
между ними совместимую и полную гипотезу.
3. Может рассматриваться еще один тип усовершенствования, который
предусматривает замену переменных структурированными термами:
member(X1, L1) :- member(X1, L3) .
может быть преобразовано в процессе усовершенствования в
member(X1, [Х2 | L2]) :- member(X1, L3).
В результате усовершенствования переменная L1 преобразуется
в структуру [Х2 | L2].
129
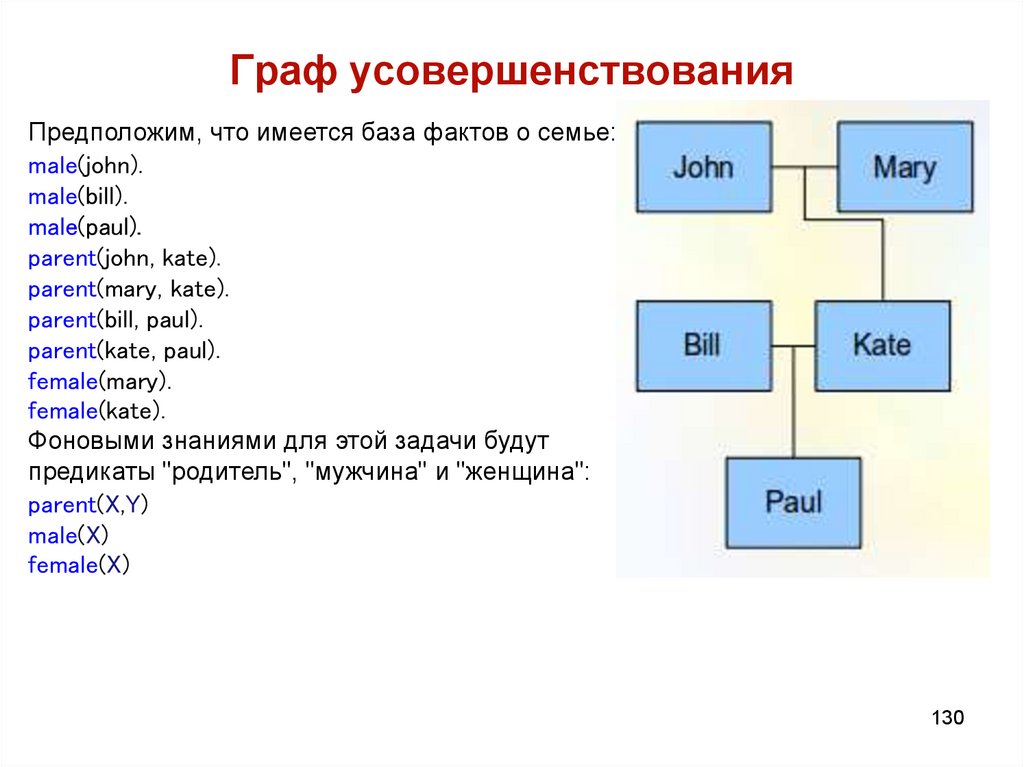
130. Граф усовершенствования
Предположим, что имеется база фактов о семье:male(john).
male(bill).
male(paul).
parent(john, kate).
parent(mary, kate).
parent(bill, paul).
parent(kate, paul).
female(mary).
female(kate).
Фоновыми знаниями для этой задачи будут
предикаты "родитель", "мужчина" и "женщина":
parent(X,Y)
male(X)
female(X)
130
131. Граф усовершенствования
Мы хотим научить ILP-систему предикату "имеет дочь".Определим его как целевой предикат:
has_daughter(X)
Для этого предиката положительные примеры будут:
has_daughter(mary)
has_daughter(john)
Отрицательные примеры:
has_daughter(bill)
has_daughter(kate)
has_daughter(paul)
131
132. Граф усовершенствования
На первом шаге обучения мы имеем только одну максимально общую гипотезу:has_daughter(X).
Она устроена тривиально - охватывает все примеры (выполняется для любого X). Но
очевидно, что на некоторых примерах она дает неправильный результат - так, в базе
есть и те, кто не имеют дочь (это Билл, Кейт и Пол). Таким образом, гипотеза полна
(охватывает все "+"-примеры), но несовместна (охватывает некоторые "-"-примеры).
Начнем процесс уточнения гипотезы.
Так как отождествлять переменные мы не можем - она всего одна - то воспользуемся
вторым способом - добавление фонового предиката к телу. Мы получим уже 3 гипотезы:
has_daughter(X):- male(Y).
has_daughter(X):- female(Y).
has_daughter(X):- parent(Y, Z).
132
133. Граф усовершенствования
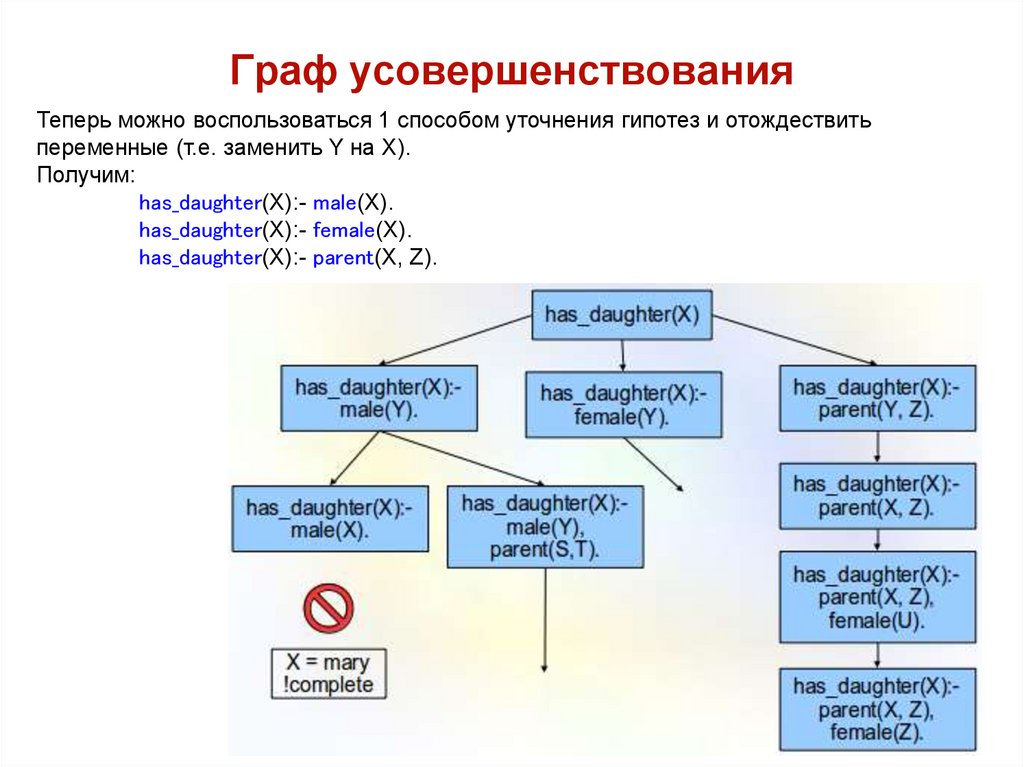
Теперь можно воспользоваться 1 способом уточнения гипотез и отождествитьпеременные (т.е. заменить Y на X).
Получим:
has_daughter(X):- male(X).
has_daughter(X):- female(X).
has_daughter(X):- parent(X, Z).
133
134. Граф усовершенствования
134135. ILP
Возможности:• Обучение рекурсивным понятиям, таким как "потомок".
• Мультипредикатное обучение (одновременное изучение нескольких предикатов, когда
один предикат определяется в терминах другого).
Недостатки:
• Требуется вручную указать количество и тип переменных в целевом предикате.
• Высокая вычислительная сложность (NP-полная задача). При добавлении литералов
увеличивается число переменных в предикате. Любое подмножество переменных
может быть отождествлено между собой, что сразу дает экспоненциальный рост
сложности.
Эвристики:
Возможные ограничения для уменьшения временных затрат:
• Ограничение на максимальную глубину поиска
• Ограничение на максимальное число литералов в теле предиката
• Введение параметра "стоимость гипотезы":
Cost(H) = количество_переменных(H) + 10*количество_литералов(H) + 10*NegCover(H)
135































































































































 Программирование
Программирование