Периодические несинусоидальные цепи. Тема №6

1. МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ  ИРКУТСКИЙ ФИЛИАЛ  КАФЕДРА АВИАЦИОННЫХ ЭЛЕКТРОСИСТЕМ И

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ГРАЖДАНСКОЙ АВИАЦИИ
ИРКУТСКИЙ ФИЛИАЛ
КАФЕДРА АВИАЦИОННЫХ ЭЛЕКТРОСИСТЕМ И ПИЛОТАЖНОНАВИГАЦИОННЫХ КОМПЛЕКСОВ
ЛЕКЦИЯ № 6
по дисциплине
Электротехника
ТЕМА № 6
Периодические несинусоидальные цепи

2. Вопросы лекции

6.1. Понятие о несинусоидальных периодических эдс,
токах и напряжениях.
6.2. Разложение несинусоидальных периодических токов,
эдс и напряжений в гармонический ряд.
6.3. Различные случаи несимметрии графиков
несинусоидальных периодических функций и
структура гармонического ряда.
6.4. Средние и действующие несинусоидальные
периодические токи, эдс и напряжения.
6.5. Коэффициенты, характеризующие форму
несинусоидальных периодических функций.

3. 6.1. Понятие о несинусоидальных периодических эдс, токах и напряжениях.

Несинусоидальными периодическими называют ЭДС, токи и напряжения,
изменяющиеся во времени по несинусоидальному периодическому закону.
Они возникают, если:
источник ЭДС (источник тока) вырабатывает несинусоидальную ЭДС (ток), а
все элементы цепи линейные;
источник ЭДС (источник тока) вырабатывает синусоидальную ЭДС (ток), но
один или несколько элементов цепи нелинейные.
С несинусоидальными ЭДС, токами и напряжениями приходится работать в
электронике, телемеханике, автоматике, в электро- и радиотехнике, в
вычислительной и измерительной технике.
Форма несинусоидальных ЭДС, токов и напряжений может быть различной.
u
u
t
а)
б)
e
e
i
t
t
t
в)
г)
Рис. 6.1.1
t
д)

4.

Для питания электронных устройств широко используются блоки питания,
на выходе которых действуют напряжения, полученные в результате
однополупериодного (рис.6.1.1, а) или двухполупериодного (рис.6.1.1, б)
выпрямления синусоидальной ЭДС или напряжения. В измерительных и
цифровых устройствах очень часто на входе действуют сигналы пилообразной
или прямоугольной формы (рис.6.1.1, в, г)
В цепях, содержащих катушку индуктивности с ферромагнитным
сердечником, даже при синусоидальных ЭДС, ток изменяется по
несинусоидальному закону (рис.6.1.1, д).
Анализ работы подобных устройств связан с расчетом режимов работы
линейных цепей, в которых действуют несинусоидальные источники
напряжения или тока.

5.

Сущность расчета таких цепей заключается в следующем:
- несинусоидальные периодические ЭДС, напряжения или токи, заданные в
схеме с помощью аппарата гармонического анализа представляются в виде
рядов Фурье, которые в общем случае содержат постоянную составляющую,
основную или первую гармонику, имеющую период, равный периоду самой
функции, и высшие гармоники, частота которых в целое число раз больше
частоты первой гармоники;
производится расчет:
= цепи для каждой из гармоник в отдельности;
= для постоянной составляющей по методам расчета цепей постоянного тока,
при этом R r ; t 0 ; 1 ;
C
= для каждой гармоники по методам расчета цепей синусоидального
переменного тока, учитывая, что для катушки X KL K ω L , а для конденсатора
1
X KC
;
K ωC
- действительные токи ветвей и напряжения на ветвях схемы определяются
как алгебраические суммы токов и напряжений отдельных составляющих, т.е.
по принципу наложения.
ЗАМЕЧАНИЕ. При разложении в ряд несинусоидальных функций
получается бесконечный ряд. На практике обычно используются первые
гармоники ряда. Число гармоник при расчете определяется необходимой
точностью.

6. 6.2. Разложение несинусоидальных периодических токов, эдс и напряжений в гармонический ряд.

В гармонический тригонометрический ряд (ряд Фурье) могут быть
разложены несинусоидальные периодические функции, удовлетворяющие
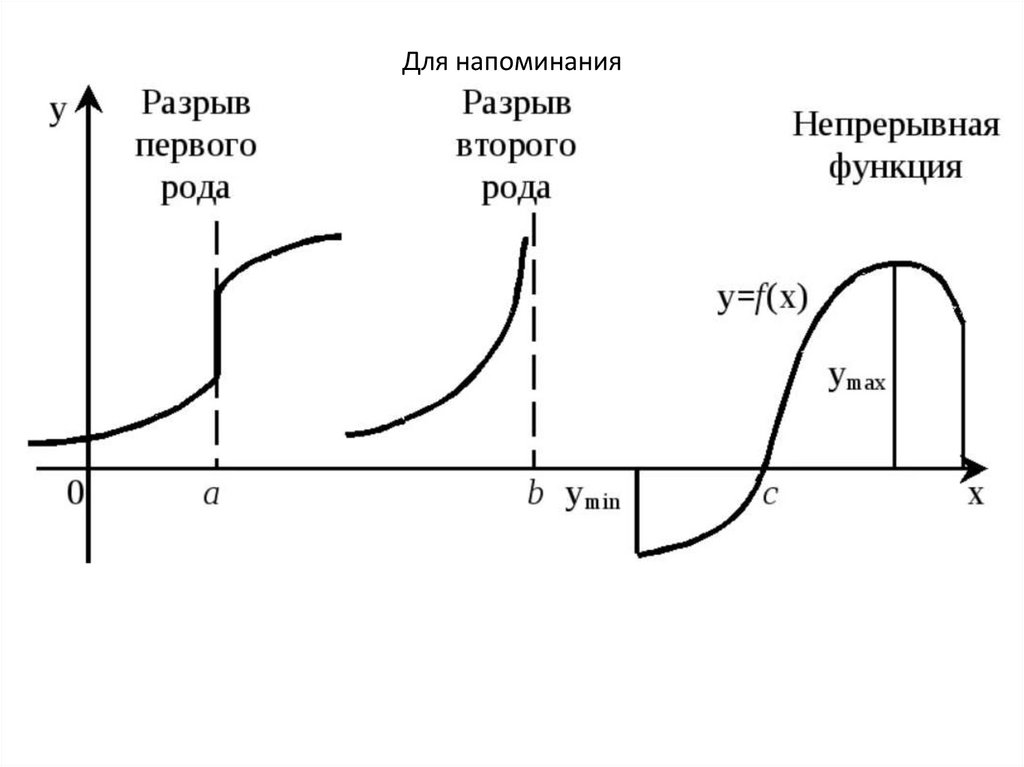
условиям Дирихле, т.е. имеющих за полный период конечное число разрывов
первого рода и конечное число максимумов и минимумов. Этим условиям
всегда удовлетворяют ЭДС, напряжения и токи в реальных физических цепях.
Ряд Фурье может быть представлен в двух формах.
Первая форма имеет вид:
f ω t f ω t 2 n A0 A1m sin ω t ψ1 A2 m sin 2 ω t ψ2
A
sin k ω t ψ А0 A
sin k ω t ψ
km
k
k
m
k
k 1
(6.2.1)
где А0 – постоянная составляющая;
A1m sin ω t ψ1
– первая или основная гармоника, а все остальные
члены ряда вида, Ak m sin k ω t ψk при k 1 – высшие гармоники;
A
k m – амплитуда k-ой гармоники;
ψ – начальная фаза k-ой гармоники;
k
K – номер гармоники

7. Для напоминания

8. Для напоминания

9.

Вторая форма записи тригонометрического ряда Фурье может быть получена
из уравнения (6.2.1), если раскрыть синус суммы для каждой гармоники, т.е.
f t A0 А1m cos ψ1 sin ω t А2m cos ψ2 sin 2 ω t
А
cos ψ sin k ω t А1m sin ψ1 cos ω t А2m sin ψ2 cos 2 ω t
km
k
A sin ψ cos k ω t A0 B
sin k ω t C
cos k ω t
km
k
k
m
k
m
k 1
k 1
где
(6.2.2)
B
А
cos ψ
km
km
k - синусная составляющая k-ой гармоники;
C
km
А
sin ψ
km
k - косинусная составляющая k-ой гармоники;
(6.2.3)
Bkm и Ckm - коэффициенты разложения;
Ψk - начальная фаза k-й гармоники.
Совокупность постоянной составляющей, основной гармоники и высших
гармонических составляющих называется спектром несинусоидальной
величины.
Тригонометрический ряд Фурье, как правило, быстро сходится, поэтому для
инженерных расчетов количество гармоник ограничивают и учитывают только
первые 3 – 5 гармоник ряда.

10.

Постоянная составляющая и коэффициенты ряда (6.2.1), (6.2.2)
определяются по следующим соотношениям:
2
1
A0
f ω t d ω t ;
2 0
1
2
B
km
C
km
f ω t sin k ω t d ω t ;
0
2
f ω t cos k ω t d ω t ;
1
0
Зная значения Bkm и Ckm , определяется Akm и Ψ k
A
B2 C 2 ;
km
km
km
C
km
ψ arctg
k
B
km
где k=1, 2… .
(6.2.4)

11.

Из выражений (6.2.4) для постоянной составляющей A0 следует, что она
представляет собой среднее значение несинусоидальной функции за период
основной гармоники.
Гармонические составляющие в рядах (6.2.1) и (6.2.2), для которых k –
четное число, называются четными гармониками, а те, для которых k –
нечетное число, называются нечетными гармониками.
Таким образом, к примеру, несинусоидальный источник напряжения можно
представить упрощенно как схему, изображенную на рисунке 6.2.1
Рис. 6.2.1

12.

Пример разложения несинусоидальной ЭДС
e(t)= 60+ 50.93 sin(3142t+π)+25.465sin(6282t+π)+16.977sin(9423t+π), В.
несинусоидальная ЭДС
а
б
Графики спектров: а) АЧХ, б) ФЧХ

13.

Заданная кривая несинусоидальной ЭДС и кривая, полученная в результате
сложения постоянной составляющей и первых трѐх гармонических
составляющих ряда. Построение осуществлено в среде MathCad.
u2(t1)
u1(t1)
u3(t1)

14. 6.3. Различные случаи несимметрии графиков несинусоидальных периодических функций и структура гармонического ряда.

В зависимости от вида графиков несинусоидальных периодических функций
может меняться структура гармонического ряда Фурье. В некоторых случаях
несинусоидальная функция имеет не полный состав в ряду разложения.
Выясним для наиболее распространенных функций состав ряда.
1. Несинусоидальная функция симметричная относительно оси абсцисс.
Функция называется симметричной относительно оси абсцисс (рис.6.3.1),
если она удовлетворяет условию: f t f t
f(ωt)
Рис. 6.3.1
t
T/2
Функция такого вида в разложении не
t
имеет постоянной составляющей (А0) и
ω
четных гармоник.
t
ω
t
π

15.

2. Несинусоидальная функция четная, симметричная относительно оси
ординат.
f t f t
Функция четная, если
(рис. 6. 3.2).
f(ωt)
Fm
f(-ωt)
Рис. 6.3.2
Функция этого вида в разложении не имеет
синусоид., т.е.
ωt
f(ωt)
f ω t А0 C1m cos ωt C2m cos 2 ωt C3m cos 3 ωt
3. Несинусоидальная функция нечетная, симметричная относительно начала
координат.
Несинусоидальная функция называется нечетной, если f t f t
(рис. 6.3.3)
f(ωt)
Fm
-f(-ωt)
f(ωt)
ωt
Рис. 6.3.3
Функция этого вида не содержит
постоянной составляющей и косинусоид.
f ω t В1m sin ωt В2m sin 2 ωt В3m sin 3 ωt

16. 6.4. Средние и действующие несинусоидальные периодические токи, эдс и напряжения.

Пусть задана несинусоидальная функция:
f t F0 F
sin k ω t ψ F
sin k ω t ψ
k
m
k
k
m
k
K 1
K 0
(6.4.1)
В электротехнике и радиотехнике пользуются понятием среднего
значения функции, взятой по абсолютной величине, которое выражается
T
интегралом вида:
1
FСР f ω t d ω t
T0
Этот интеграл функции равен среднему значению функции f t за
положительный полупериод, если f t имеет одинаковые положительную и
отрицательную полуволны.
T
T /2
1
2
FCP f ω t d t f ω t d t
(6.4.2)
T0
T 0
Среднее значение функции за полупериод измеряется с помощью
магнитоэлектрического прибора с выпрямителем (магнитоэлектрический
прибор без выпрямителя измеряет постоянную составляющую). (в качествеf t
может быть i ω t , u ω t или e ω t ).

17.

Действующее значение F периодической несинусоидальной функции по
аналогии с определением действующего значения синусоидальной функции
определяется как среднеквадратичное из квадрата по формуле:
2
1
1
2
F
f
ω
t
d
t
F
F
sin
k
ω
t
ψ
dt
0
km
k
T 0
T 0
k 1
T
T
(6.4.3)
Интеграл, стоящий под корнем в уравнении (6.4.3), с учетом выражения
(6.4.1) можно представить как сумму интегралов, разбив его на три группы.
В первую группу войдет интеграл вида:
T
1
2
2
F
d
t
F
0
0
T 0
(6.4.4)
Во вторую группу войдут интегралы от квадратов синусоид вида:
1
1
2
2
2
2
F
sin
k
ω
t
ψ
d
t
F
sin
k ωt ψ d t
km
k
km
k
T 0 k 1
k 1 T 0
T
T
2
F
km
F 2
k
2
k 1
k 1
(6.4.5)

18.

К такому результату пришли, воспользовавшись формулой преобразования
и подставив ее в подинтегральное значение уравнения (6.4.5). Это позволило
представить интегралы вида (6.4.5) как разность двух интегралов.
0
2
T F
1T F 2
1
1
2
2
F
sin k ωt ψ d t km d t km cos 2 k ωt 2 ψ d t
km
k
k
2
T 0 2
k 1 T 0
k 1 T 0
T
где вторые из них равны нулю как интегралы за период от косинусоидальной
функции, а первые
2
2
F
1 Fkm
2
km
d
t
F
2
k
2
k 1 T 0
k 1
k 1
T
В третью группу будут входить интегралы от произведения синусоид разных
частот вида
T
1
F Fnm sin k ωt ψ sin n ωt ψn d t 0
k
T 0 k 1 km
n 1
k n
(6.4.6)
Интегралы в уравнении (6.4.6) равны нулю потому, что после
преобразования
cos k n ωt ψ n cos k n ωt ψ n
k
k
sin k ωt ψ sin n ωt ψn
k
2

19.

интегралы в уравнении (6.4.6) могут быть заменены разностью двух
интегралов, каждый из которых равен нулю, как интеграл за период от
косинусоидальной функции.
Тогда с учетом (6.4.4) и (6.4.5), выражение для (6.4.3) можно представить:
F
F02
Fk Fk2
2
F02 F12 F22
(6.4.7)
Итак, действующее значение несинусоидальной периодической функции
равно корню квадратному от суммы квадратов постоянной составляющей и
действующих значений отдельных гармоник.
Так как под F могут пониматься действующие значения ЭДС, тока и
напряжения, то
T
k 1
E
k 0
1 2
2
2
2
e
t
d
t
F
F
F
0
1
2
T0
I I 02 I 12 I 22
(6.4.8)
U U 02 U 12 U 22
Действующее значение периодической несинусоидальной функции может
быть измерено, так же как при синусоидальных токах и напряжениях, с
помощью электроизмерительных приборов электромагнитной,
электродинамической, тепловой или других систем.

20. Мощность при несинусоидальных напряжениях и токах

Под активной мощностью (Р, Вт) несинусоидального тока понимают
среднее значение мгновенной мощности за период первой гармоники:
(6.4.9)
Если представить напряжение u и ток i рядами Фурье
и подставить эти ряды в выражение (6.4.9), то можно получить:
(6.4.10)
где φK - угол между U K и IK .
Таким образом, активная мощность несинусоидального тока равна сумме
активных мощностей отдельных гармоник.

21.

Аналогично выводится понятие реактивной мощности(Q, ВАр):
(6.4.11)
Полная мощность (S, ВА) равна произведению действующего значения
несинусоидального напряжения на действующее значение несинусоидального
тока:
(6.4.12)
где
В цепях c несинусоидальными токами в отличие от синусоидальных цепей
(6.4.13)
так как в них действует мощность искажения (Т, ВАр), обусловленная наличием
высших гармоник
(6.4.14)
(6.4.15)

22.

Отношение активной мощности к полной называется коэффициентом
мощности
(6.4.16)
Для синусоидальных цепей λ=cosφ , но в несинусоидальных цепях
появляется коэффициент искажения.
(6.4.17)
где Kи - коэффициент искажения.

23. 6.5. Коэффициенты, характеризующие форму несинусоидальных периодических функций.

Для характеристики формы несинусоидальных периодических кривых
используют, следующие коэффициенты:
- коэффициент амплитуды КА;
- коэффициент формы кривой КФ;
- коэффициент искажения КИ
- коэффициент гармоник .
Коэффициентом амплитуды называется отношение максимального
значения к действующему: K Fm
A
F
Для синусоиды
K A 2 1,41
Коэффициентом формы несинусоидальной периодической кривой,
симметричной относительно оси абсцисс, называется отношение действующего
значения к среднему за половину периода:
F
KФ
Для синусоиды
FCP
Fm 2
KФ
: Fm
1,11
2
2 2

24.

Коэффициентом искажения называется отношение действующего
значения основной гармоники к полному действующему значению:
F1
KИ
F
Для синусоиды K И 1 .
В электротехнике и радиотехнике для оценки искажений пользуются
коэффициентом гармоник, который определяется как отношение
действующего значения высших гармоник к действующему значению основной
гармоники:
1
K
F1
2
F
k
k 2
1
K
KИ
1 KИ
При отсутствии постоянной составляющей
Для синусоиды K=0
Комплексным коэффициентом передачи электрической цепи называют
отношение выходной величины (на нагрузке) к входной в комплексной форме
записи.
2

25. заключение

Таким образом, в результате рассмотрения материала вы получили знания :
о несинусоидальных периодических эдс, токах и напряжениях;
о разложении несинусоидальных периодических токов, эдс и
напряжений в гармонический ряд;
о различных случаях несимметрии графиков несинусоидальных
периодических функций и структуре гармонического ряда;
о средниих и действующих несинусоидальных периодических токах, эдс
и напряжениях;
о коэффициентах, характеризующих форму несинусоидальных
периодических функций.