Похожие презентации:
Типы отношений
1. Типы отношений
2. Отношение эквивалентности
Бинарноеотношение
называется
отношением эквивалентности (обозначается ~),
если оно
1) рефлексивно;
2) симметрично;
3) транзитивно.
Пример.
R1 — “=” на любом множестве.
R2 — “учиться в одной группе” на множестве
студентов университета.
2
3. Отношение порядка
Бинарное отношение называется отношениемчастичного порядка (обозначается ), если оно
1) рефлексивно;
2) антисимметрично;
3) транзитивно.
Пример.
R1 — “являться нестрогим включением”,
заданное на системе множестве.
Если на множестве задано отношение
частичного порядка, то это множество называется
частично упорядоченным.
3
4. Отношение порядка
Отношение частичного порядка такженазывается отношением нестрогого порядка.
В отличии от него отношение строгого
порядка (обозначается <):
1) антирефлексивно (если a<b, то a b)
2) асимметрично (если a<b то не верно b<a)
3) транзитивно (если a<b и b<c, то a<c).
Пример.
R1 — “>” на любом множестве.
4
5. Отношение толерантности
Отношение называется отношениемтолерантности, если оно:
1) рефлексивно;
2) симметрично;
5
6. Отношение доминирования
Отношение называется отношениемдоминирования , если оно:
1) антирефлексивно;
2) асимметрично.
6
7. Применение свойств бинарных отношений
A={1,2,3,4};R1 A2;
R2 A2.
+
R2={(2,1),(3,1),(3,2),(4,1),
(4,2),(4,3)}.
Рефлексивность
Антирефлексивность
Симметричность
Асимметричность
Антисимметричность
Транзитивность
Антитранзитивность
Эквивалентности
Толерантности
Частичного порядка
Строгого порядка
+
+
+
+
+
-
R1={(1,1),(1,2),(1,4),(2,1),
(2,2),(3,3 ),(4,1),
(4,2),(4,4)};
R1 R2
7
8. Композиция соответствий
XZ
Y
X
1 2 3 4
a 1 1
b
1
c
d 1
e
f
1
w x
1
4
z
1
2
3
y
1
1
1
Z
w x y z
a
1 1
b
c
d
1
e
f
8
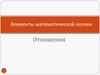
9. Композиция соответствий
1 2 3 4a 1 1
b
c
d 1
e
f
w x
1
1
4
1
z
w x y z
a
1 1
b
1
c
d
e
1
2
3
y
1
1
1
f
9
10. Композиция соответствий
1 2 3 4a 1 1
b
c
d 1
e
f
w x
1
1
4
1
z
w x y z
a
1 1
b
1
c
d
e
1
2
3
y
1
1
1
f
10
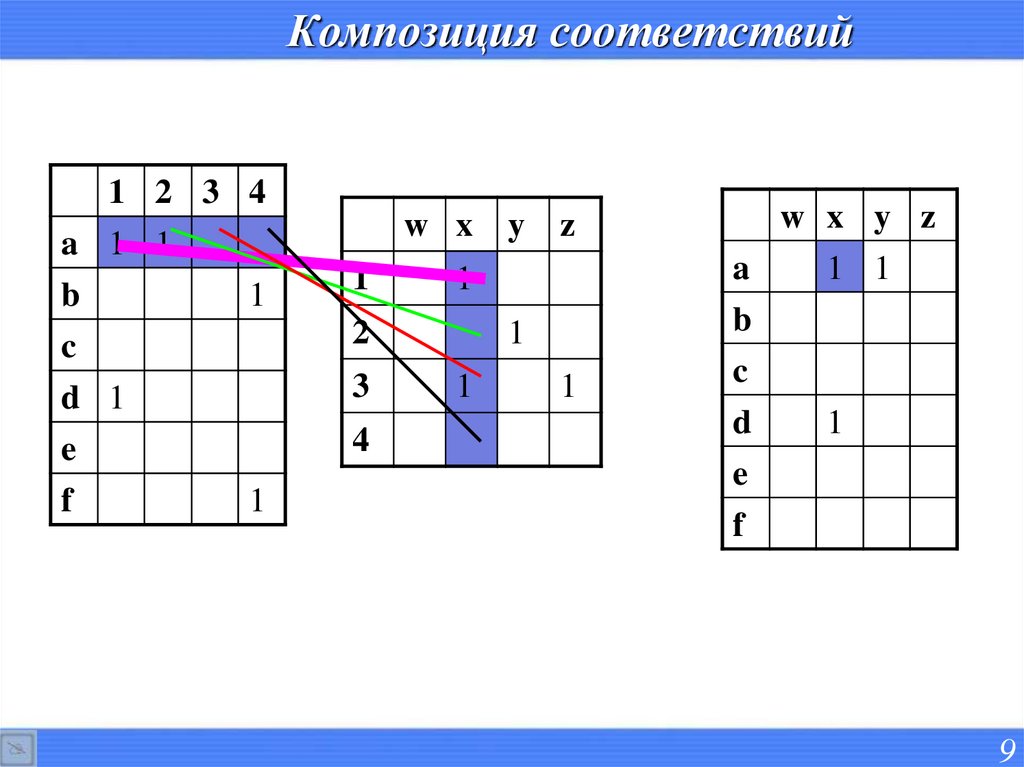
11.
Транзитивность2
1 1
1
1
3
1 1
1 x
1 1
1
1
=
11
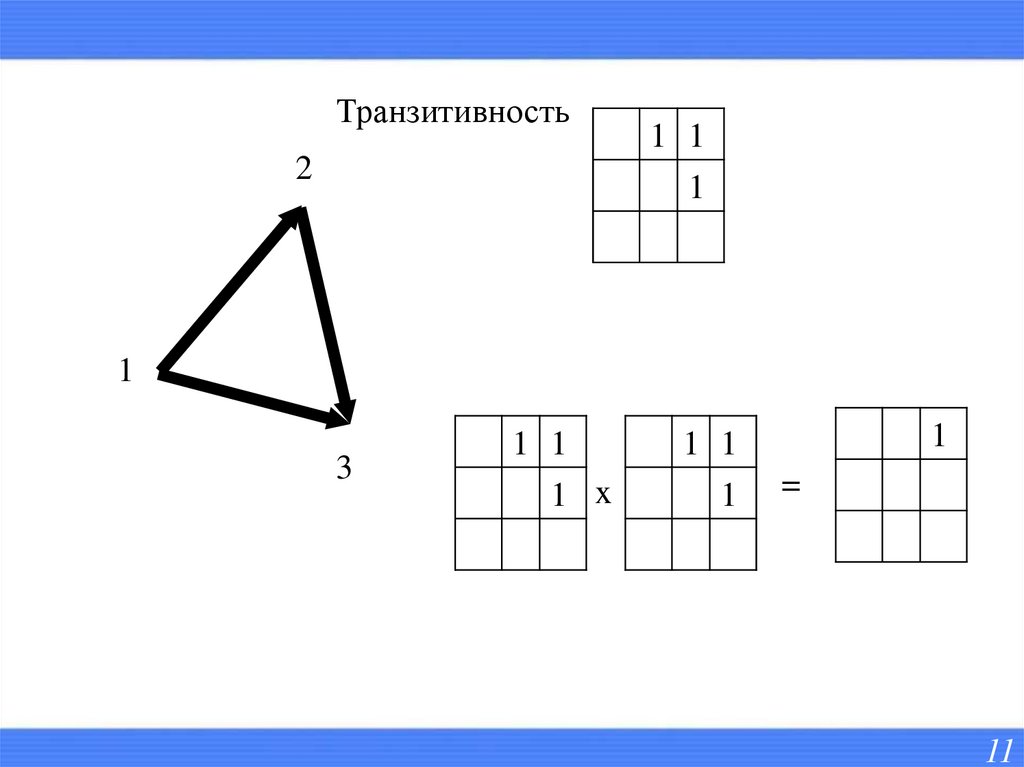
12.
Антитранзитивность1
1
1
2
1
1
4
3
1
1
1
1
1
x
1
1
1
=
1
12
13.
Под высказыванием принято понимать языковоепредложение, о котором имеет смысл говорить, что
оно истинно или ложно в данный момент времени.
Высказывание называют простым (элементарным),
если оно рассматривается как некое неделимое целое
(аналогично элементу множества).
Сложным (составным) называется высказывание,
составленное из простых с помощью логических
связок.
13
14.
Логика высказываний рассматриваетпредложения не с точки зрения их смысла,
содержания, а только с точки зрения их
истинности или ложности. Для понятия
«высказывание» иногда используют термин
«пропозиция», а говоря
«пропозициональный», подразумевают
относящийся к логике высказываний.
14
15.
Наиболее важные функции- Отрицание
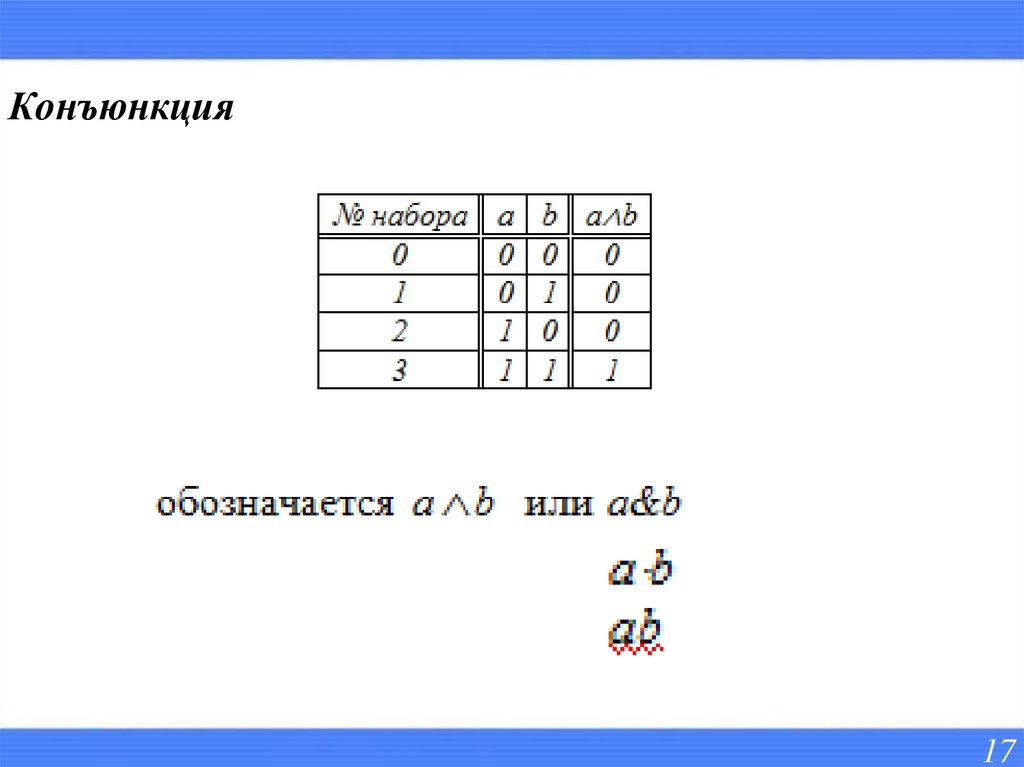
- Конъюнкция
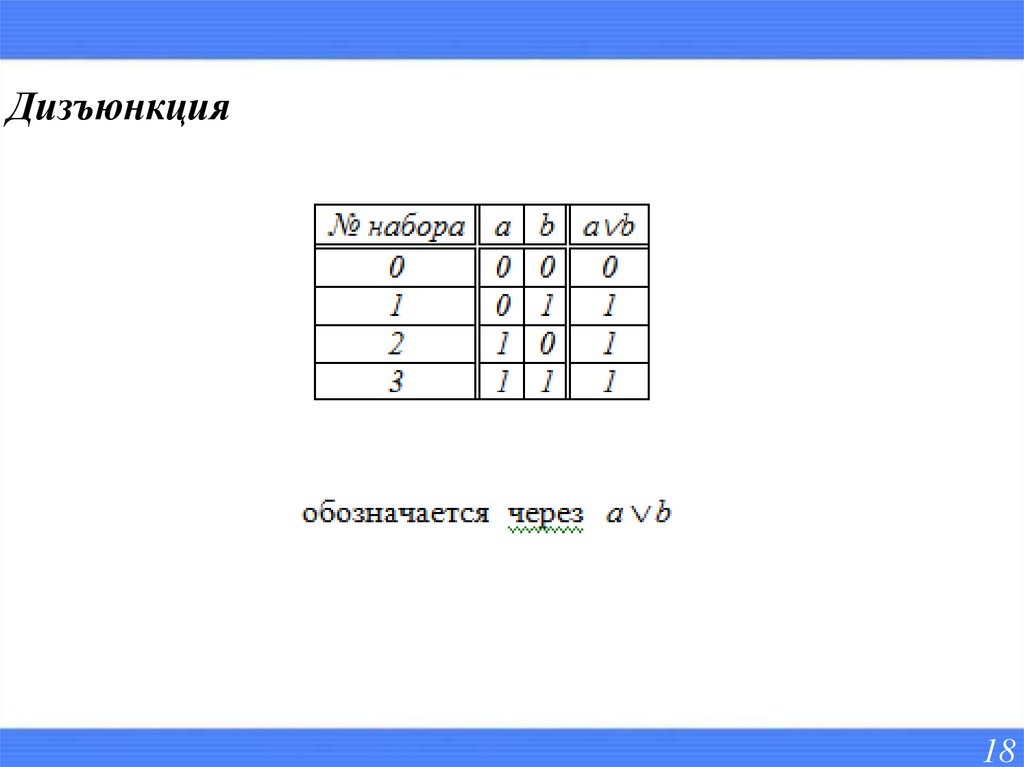
- Дизъюнкция
- Импликация
- Эквиваленция (или эквивалентность)
15
16.
Отрицание16
17.
Конъюнкция17
18.
Дизъюнкция18
19.
Импликация19
20.
Эквиваленция20
21. Формулы логики высказываний
Формулы логики высказываний, соответствующие сложным высказываниям, принимаютзначение И или Л в зависимости от значений
элементарных высказываний, из которых они
построены, и логических связок.
Приписывание истинностных значений атомам называется интерпретацией высказывания.
21
22. Формулы логики высказываний
ПримерP Q R (P~R)
в интерпретации
(P ,Q, R)=(И,Л,И)
принимает значение
P Q R (P~R)
И Л И И И
Л Л И
И
И
22
23.
Слово в алфавите логики высказываний называетсяформулой, если оно удовлетворяет следующему
определению:
любая высказывательная переменная – формула;
если А и В – формулы, то А, А В, А В, А В,
А В, А В, А В, А В – формулы;
только те слова являются формулами, для которых
это следует из 1) и 2).
Подформулой формулы А называется любая ее часть,
которая сама является формулой.
23
24. Виды формул
Формула называется тождественно истинной(тавтологией или общезначимой), если она принимает
значение «Истина» на всех наборах значений входящих в
нее переменных (во всех интерпретациях).
Формула называется тождественно ложной
(противоречивой или невыполнимой), если она
принимает значение «Ложь» на всех наборах значений
входящих в нее переменных.
Формула называется необщезначимой или
непротиворечивой (нейтральной), если хотя бы в одной
интерпретации она принимает значение «Истина», и хотя
бы в одной интерпретации – «Ложь».
24
25. Виды формул
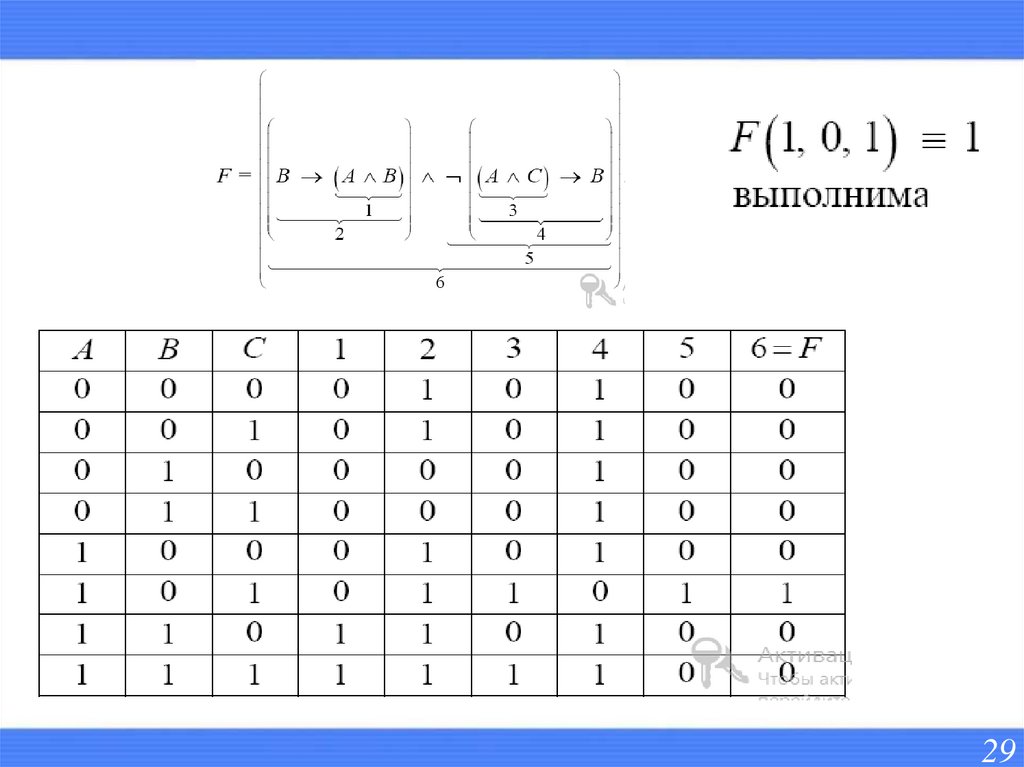
Формула называется выполнимой, если хотябы в одной интерпретации она принимает значение
«Истина»
Формула называется необщезначимой, если
хотя бы в одной интерпретации она принимает
значение «Ложь».
25
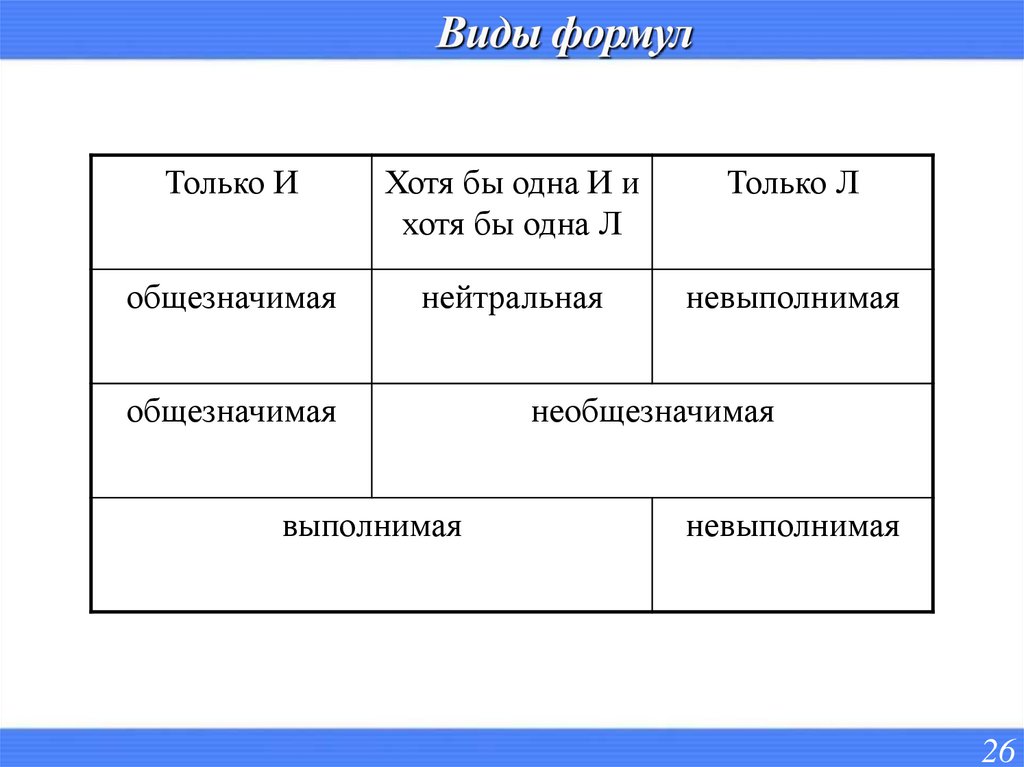
26.
Только ИХотя бы одна И и
хотя бы одна Л
Только Л
общезначимая
нейтральная
невыполнимая
общезначимая
выполнимая
необщезначимая
невыполнимая
26
27.
Пусть А и В – две формулы, зависящие от одного итого же списка переменных. Будем называть их
равносильными, если для любого набора значений
переменных они принимают одинаковые значения
Способы проверки:
Таблицы истинности
Преобразования
27
28.
2829.
2930.
свойства логических операций30
31.
3132.
3233. Применение алгебры высказываний
Определение структуры предложенийАнализ рассуждений
Анализ и синтез контактных схем
Анализ и синтез электронных схем
33
34.
3435. Определение структуры предложений. Пример 2
Диагонали параллелограмма пересекаются и в точкепересечения делятся пополам
P: Диагонали параллелограмма пересекаются
Q: Диагонали параллелограмма в точке пересечения
делятся пополам
P Q
35
36. Определение структуры предложений. Пример 2
Диагонали параллелограмма пересекаютсяP: ABCD параллелограмм
Q: Диагонали AC и BD пересекаются
P Q
36
37. Анализ рассуждений. Пример 1
Если число четно, то оно делится на 2. Заданноечисло четно. Значит оно делится на 2.
A: Заданное число четно
B: Заданное число делится на 2
A B, A ╞ B
╞ (A B) A B
37
38.
3839.
3940.
4041.
4142.
4243. Анализ рассуждений. Пример 2
Определить, Был ли Смит убийцей, если известноследующее:
Если Джонс не встречал этой ночью Смита, то либо
Смит был убийцей, либо Джонс лжет. Если Смит не
был убийцей, то Джонс не встречал Смита этой
ночью, и убийство имело место после полуночи. Если
убийство было совершено после полуночи, то либо
Смит был убийцей, либо Джонс лжет.
43
44. Анализ рассуждений. Пример2
элементарные высказывания:А – Джонс не встречал Смита этой ночью.
В – Смит был убийца.
С – Джонс лжет.
D – убийство было совершено после полуночи.
44
45. Анализ рассуждений. Пример2
А – Джонс не встречал Смита этой ночью.В – Смит был убийца.
С – Джонс лжет.
D – убийство было совершено после полуночи.
45
46. Анализ рассуждений. Пример2
А – Джонс не встречал Смита этой ночью.В – Смит был убийца.
С – Джонс лжет.
D – убийство было совершено после полуночи.
Либо Смит был убийцей, либо убийство совершено после полуночи Джонс лжет,
что не видел Смита этой ночью. Последнее сложное высказывание по сути также
определяет вину Смита, как и прямое утверждение, что Смит был убийцей. Таким
образом приговор Смиту вынесен.
46
47.
Встретились три одноклассника: Белов, Рыжов и Чернов.Черноволосый сказал, что ни у одного из них цвет не
соответствует фамилии. Правильно! - ответил Белов.
Напиши, какого цвета волосы у каждого из мальчиков.
б
ч
р
Б
0
0
1
Ч
1
0
0
Р
0
1
0
47
48.
Задача 11 Комната
2 Комната
В этой комнате
В одной из этих комнат
находится принцесса, а в находится принцесса;
другой комнате сидит
кроме того, в одной из
тигр.
этих комнат сидит тигр.
Дополнительно было известно следующее:
на одной табличке написана правда, а на другой нет .
определить, в какой комнате принцесса.
49.
Решение задачи 1Для каждой из табличек возможны только два варианта, либо
ложь, либо истина. Рассмотрим с этой позиции табличку на
первой комнате.
Табличка на первой двери истинна. Тогда табличка на второй
двери ложна. А так как табличка на второй двери утверждает,
что в одной из комнат находится принцесса, то из её
ложности следует, что принцессы там нет, что приходит в
противоречие с истинностью первой таблички. Таким
образом, мы, предположив, что табличка на первой двери
истинна, пришли к противоречию.
50.
Решение задачи 1Табличка на первой двери ложна. Тогда табличка на второй
двери истинна. Из ложности первой таблички следует, что
принцесса находится в комнате 2, а тигр в комнате 1. Из
истинности второй табличке следует, что в одной из комнат
есть принцесса и в одной из комнат есть тигр. Эти
утверждения не противоречат друг другу, следовательно
вторая ситуация непротиворечива и чего в свою очередь
следует что принцесса находится во второй комнате.
51.
Решение задачи 11 Комната
Элементарные высказывания:
В этой комнате
А – В первой комнате принцесса. находится принцесса, а
в другой комнате сидит
В – Во второй комнате тигр.
тигр.
2 Комната
В одной из этих комнат
находится принцесса;
кроме того, в одной из
этих комнат сидит тигр.
Тогда, надписи на комнатах можно записать следующим
образом
1 Комната:
X: AB
2 Комната:
Y: AB A B .
Т.к. на одной табличке написана правда, а на другой нет,
получаем XY XY AB AB A B AB ( AB A B )
AB ( A B )( A B) ( A B )( AB A B )
AB
т.е. в первой комнате тигр, а во второй принцесса.
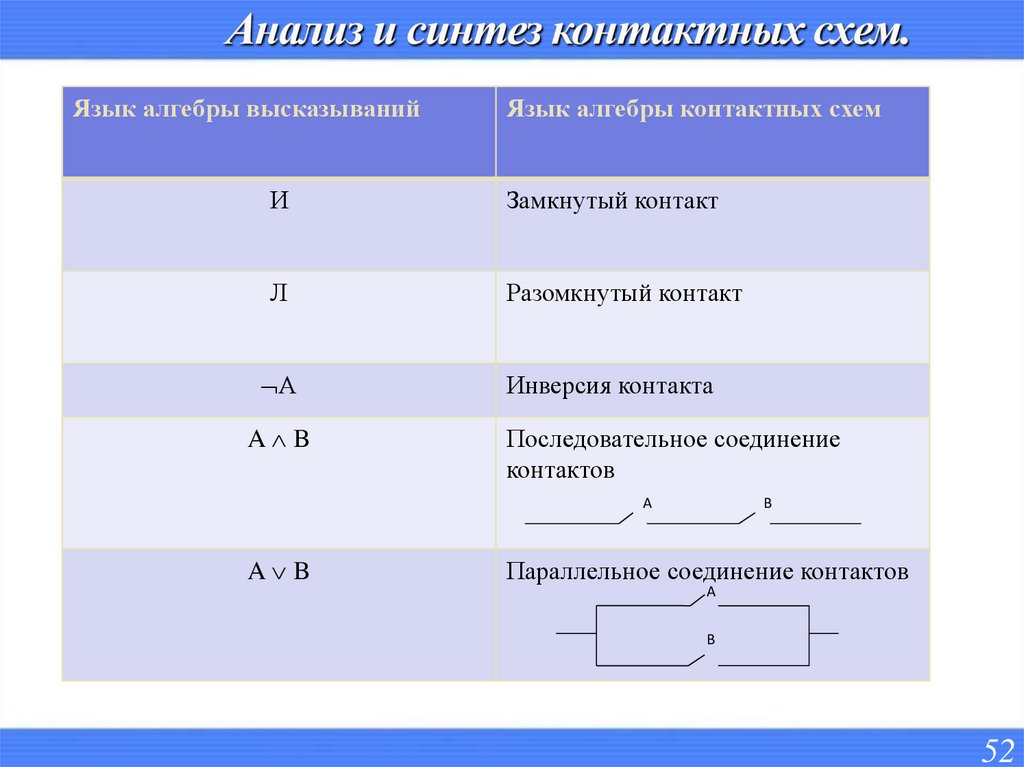
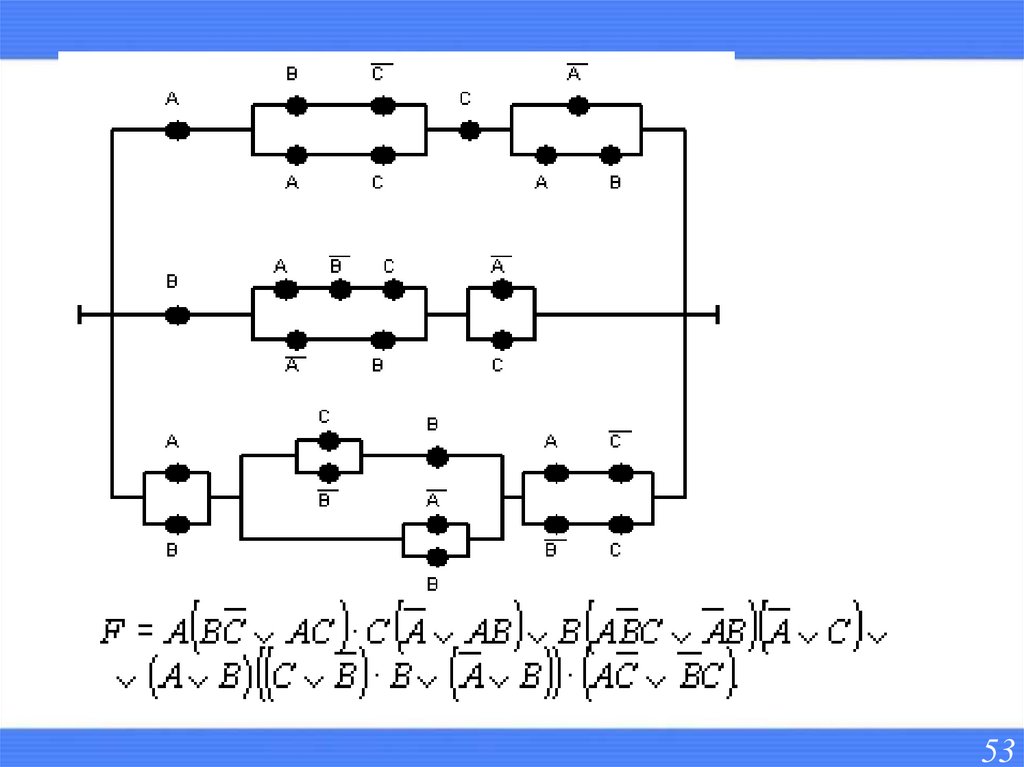
52. Анализ и синтез контактных схем.
Язык алгебры высказыванийЯзык алгебры контактных схем
И
Замкнутый контакт
Л
Разомкнутый контакт
А
Инверсия контакта
A B
Последовательное соединение
контактов
A
A B
B
Параллельное соединение контактов
A
B
52













































 Математика
Математика Информатика
Информатика