Похожие презентации:
Функции нескольких переменных
1.
Основные понятия Предел функции Непрерывность функции Частные производныеФункции нескольких переменных
К.А. Смотрицкий
Гродненский государственный университет имени Янки Купалы
2022
К.А. Смотрицкий
Функции нескольких переменных
2.
Основные понятия Предел функции Непрерывность функции Частные производныеСодержание
1
Основные понятия
2
Предел функции
3
Непрерывность функции
4
Частные производные
К.А. Смотрицкий
Функции нескольких переменных
3.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Обозначим через R2 множество всех упорядоченных пар
чисел (x, y).
Пусть D — некоторое множество из R2 , D ⊂ R2 .
Соответствие f , которое каждой паре чисел (x, y) ∈ D
сопоставляет единственное число z ∈ R, называется функцией
2-х переменных, определенной на множестве D.
z = f (x, y),
f : D → R.
Множество D называется областью определения функции и
обозначается D(f ).
Множество значений, принимаемых функцией в области
определения, обозначается через E(f ), E(f ) ⊂ R.
К.А. Смотрицкий
Функции нескольких переменных
4.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Обозначим через R2 множество всех упорядоченных пар
чисел (x, y).
Пусть D — некоторое множество из R2 , D ⊂ R2 .
Соответствие f , которое каждой паре чисел (x, y) ∈ D
сопоставляет единственное число z ∈ R, называется функцией
2-х переменных, определенной на множестве D.
z = f (x, y),
f : D → R.
Множество D называется областью определения функции и
обозначается D(f ).
Множество значений, принимаемых функцией в области
определения, обозначается через E(f ), E(f ) ⊂ R.
К.А. Смотрицкий
Функции нескольких переменных
5.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Обозначим через R2 множество всех упорядоченных пар
чисел (x, y).
Пусть D — некоторое множество из R2 , D ⊂ R2 .
Соответствие f , которое каждой паре чисел (x, y) ∈ D
сопоставляет единственное число z ∈ R, называется функцией
2-х переменных, определенной на множестве D.
z = f (x, y),
f : D → R.
Множество D называется областью определения функции и
обозначается D(f ).
Множество значений, принимаемых функцией в области
определения, обозначается через E(f ), E(f ) ⊂ R.
К.А. Смотрицкий
Функции нескольких переменных
6.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Обозначим через R2 множество всех упорядоченных пар
чисел (x, y).
Пусть D — некоторое множество из R2 , D ⊂ R2 .
Соответствие f , которое каждой паре чисел (x, y) ∈ D
сопоставляет единственное число z ∈ R, называется функцией
2-х переменных, определенной на множестве D.
z = f (x, y),
f : D → R.
Множество D называется областью определения функции и
обозначается D(f ).
Множество значений, принимаемых функцией в области
определения, обозначается через E(f ), E(f ) ⊂ R.
К.А. Смотрицкий
Функции нескольких переменных
7.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Обозначим через R2 множество всех упорядоченных пар
чисел (x, y).
Пусть D — некоторое множество из R2 , D ⊂ R2 .
Соответствие f , которое каждой паре чисел (x, y) ∈ D
сопоставляет единственное число z ∈ R, называется функцией
2-х переменных, определенной на множестве D.
z = f (x, y),
f : D → R.
Множество D называется областью определения функции и
обозначается D(f ).
Множество значений, принимаемых функцией в области
определения, обозначается через E(f ), E(f ) ⊂ R.
К.А. Смотрицкий
Функции нескольких переменных
8.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Обозначим через R2 множество всех упорядоченных пар
чисел (x, y).
Пусть D — некоторое множество из R2 , D ⊂ R2 .
Соответствие f , которое каждой паре чисел (x, y) ∈ D
сопоставляет единственное число z ∈ R, называется функцией
2-х переменных, определенной на множестве D.
z = f (x, y),
f : D → R.
Множество D называется областью определения функции и
обозначается D(f ).
Множество значений, принимаемых функцией в области
определения, обозначается через E(f ), E(f ) ⊂ R.
К.А. Смотрицкий
Функции нескольких переменных
9.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Обозначим через R2 множество всех упорядоченных пар
чисел (x, y).
Пусть D — некоторое множество из R2 , D ⊂ R2 .
Соответствие f , которое каждой паре чисел (x, y) ∈ D
сопоставляет единственное число z ∈ R, называется функцией
2-х переменных, определенной на множестве D.
z = f (x, y),
f : D → R.
Множество D называется областью определения функции и
обозначается D(f ).
Множество значений, принимаемых функцией в области
определения, обозначается через E(f ), E(f ) ⊂ R.
К.А. Смотрицкий
Функции нескольких переменных
10.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Таким же образом можно дать определение функции n
переменных.
В этом случае вводится n-мерное пространство Rn .
Rn — это множество всех упорядоченных последовательностей
n действительных чисел (x1 , x2 , . . . , xn ), D ⊂ Rn .
z = f (x1 , x2 , . . . , xn ),
К.А. Смотрицкий
f : D → R.
Функции нескольких переменных
11.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Таким же образом можно дать определение функции n
переменных.
В этом случае вводится n-мерное пространство Rn .
Rn — это множество всех упорядоченных последовательностей
n действительных чисел (x1 , x2 , . . . , xn ), D ⊂ Rn .
z = f (x1 , x2 , . . . , xn ),
К.А. Смотрицкий
f : D → R.
Функции нескольких переменных
12.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Таким же образом можно дать определение функции n
переменных.
В этом случае вводится n-мерное пространство Rn .
Rn — это множество всех упорядоченных последовательностей
n действительных чисел (x1 , x2 , . . . , xn ), D ⊂ Rn .
z = f (x1 , x2 , . . . , xn ),
К.А. Смотрицкий
f : D → R.
Функции нескольких переменных
13.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Таким же образом можно дать определение функции n
переменных.
В этом случае вводится n-мерное пространство Rn .
Rn — это множество всех упорядоченных последовательностей
n действительных чисел (x1 , x2 , . . . , xn ), D ⊂ Rn .
z = f (x1 , x2 , . . . , xn ),
К.А. Смотрицкий
f : D → R.
Функции нескольких переменных
14.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Таким же образом можно дать определение функции n
переменных.
В этом случае вводится n-мерное пространство Rn .
Rn — это множество всех упорядоченных последовательностей
n действительных чисел (x1 , x2 , . . . , xn ), D ⊂ Rn .
z = f (x1 , x2 , . . . , xn ),
К.А. Смотрицкий
f : D → R.
Функции нескольких переменных
15.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
1) z = 1 − x − y,
D(f ) = R2 ,
2) z =
E(f ) = R.
x2 y 2
+ 2,
a2
b
D(f ) = R2 ,
К.А. Смотрицкий
E(f ) = [0, +∞ ).
Функции нескольких переменных
16.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
1) z = 1 − x − y,
D(f ) = R2 ,
2) z =
E(f ) = R.
x2 y 2
+ 2,
a2
b
D(f ) = R2 ,
К.А. Смотрицкий
E(f ) = [0, +∞ ).
Функции нескольких переменных
17.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
1) z = 1 − x − y,
D(f ) = R2 ,
2) z =
E(f ) = R.
x2 y 2
+ 2,
a2
b
D(f ) = R2 ,
К.А. Смотрицкий
E(f ) = [0, +∞ ).
Функции нескольких переменных
18.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
1) z = 1 − x − y,
D(f ) = R2 ,
2) z =
E(f ) = R.
x2 y 2
+ 2,
a2
b
D(f ) = R2 ,
К.А. Смотрицкий
E(f ) = [0, +∞ ).
Функции нескольких переменных
19.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
1) z = 1 − x − y,
D(f ) = R2 ,
2) z =
E(f ) = R.
x2 y 2
+ 2,
a2
b
D(f ) = R2 ,
К.А. Смотрицкий
E(f ) = [0, +∞ ).
Функции нескольких переменных
20.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
1) z = 1 − x − y,
D(f ) = R2 ,
2) z =
E(f ) = R.
x2 y 2
+ 2,
a2
b
D(f ) = R2 ,
К.А. Смотрицкий
E(f ) = [0, +∞ ).
Функции нескольких переменных
21.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
1) z = 1 − x − y,
D(f ) = R2 ,
2) z =
E(f ) = R.
x2 y 2
+ 2,
a2
b
D(f ) = R2 ,
К.А. Смотрицкий
E(f ) = [0, +∞ ).
Функции нескольких переменных
22.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
1) z = 1 − x − y,
D(f ) = R2 ,
2) z =
E(f ) = R.
x2 y 2
+ 2,
a2
b
D(f ) = R2 ,
К.А. Смотрицкий
E(f ) = [0, +∞ ).
Функции нескольких переменных
23.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
1) z = 1 − x − y,
D(f ) = R2 ,
2) z =
E(f ) = R.
x2 y 2
+ 2,
a2
b
D(f ) = R2 ,
К.А. Смотрицкий
E(f ) = [0, +∞ ).
Функции нескольких переменных
24.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
3) z =
p
1 − x2 − y 2 ,
D(f ) = {(x, y) : x2 + y 2 ≤ 1},
4) z = p
1
1 − x2 − y 2
E(f ) = [0, 1] .
,
D(f ) = {(x, y) : x2 + y 2 < 1},
К.А. Смотрицкий
E(f ) = [1, +∞ ).
Функции нескольких переменных
25.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
3) z =
p
1 − x2 − y 2 ,
D(f ) = {(x, y) : x2 + y 2 ≤ 1},
4) z = p
1
1 − x2 − y 2
E(f ) = [0, 1] .
,
D(f ) = {(x, y) : x2 + y 2 < 1},
К.А. Смотрицкий
E(f ) = [1, +∞ ).
Функции нескольких переменных
26.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
3) z =
p
1 − x2 − y 2 ,
D(f ) = {(x, y) : x2 + y 2 ≤ 1},
4) z = p
1
1 − x2 − y 2
E(f ) = [0, 1] .
,
D(f ) = {(x, y) : x2 + y 2 < 1},
К.А. Смотрицкий
E(f ) = [1, +∞ ).
Функции нескольких переменных
27.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
3) z =
p
1 − x2 − y 2 ,
D(f ) = {(x, y) : x2 + y 2 ≤ 1},
4) z = p
1
1 − x2 − y 2
E(f ) = [0, 1] .
,
D(f ) = {(x, y) : x2 + y 2 < 1},
К.А. Смотрицкий
E(f ) = [1, +∞ ).
Функции нескольких переменных
28.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
3) z =
p
1 − x2 − y 2 ,
D(f ) = {(x, y) : x2 + y 2 ≤ 1},
4) z = p
1
1 − x2 − y 2
E(f ) = [0, 1] .
,
D(f ) = {(x, y) : x2 + y 2 < 1},
К.А. Смотрицкий
E(f ) = [1, +∞ ).
Функции нескольких переменных
29.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
3) z =
p
1 − x2 − y 2 ,
D(f ) = {(x, y) : x2 + y 2 ≤ 1},
4) z = p
1
1 − x2 − y 2
E(f ) = [0, 1] .
,
D(f ) = {(x, y) : x2 + y 2 < 1},
К.А. Смотрицкий
E(f ) = [1, +∞ ).
Функции нескольких переменных
30.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
3) z =
p
1 − x2 − y 2 ,
D(f ) = {(x, y) : x2 + y 2 ≤ 1},
4) z = p
1
1 − x2 − y 2
E(f ) = [0, 1] .
,
D(f ) = {(x, y) : x2 + y 2 < 1},
К.А. Смотрицкий
E(f ) = [1, +∞ ).
Функции нескольких переменных
31.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
3) z =
p
1 − x2 − y 2 ,
D(f ) = {(x, y) : x2 + y 2 ≤ 1},
4) z = p
1
1 − x2 − y 2
E(f ) = [0, 1] .
,
D(f ) = {(x, y) : x2 + y 2 < 1},
К.А. Смотрицкий
E(f ) = [1, +∞ ).
Функции нескольких переменных
32.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры
3) z =
p
1 − x2 − y 2 ,
D(f ) = {(x, y) : x2 + y 2 ≤ 1},
4) z = p
1
1 − x2 − y 2
E(f ) = [0, 1] .
,
D(f ) = {(x, y) : x2 + y 2 < 1},
К.А. Смотрицкий
E(f ) = [1, +∞ ).
Функции нескольких переменных
33.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
1) S0 — начальная сумма вклада,
x — ежегодный процент прироста,
y — количество лет.
Сумма вклада через y лет:
x y
S = S0 1 +
.
100
К.А. Смотрицкий
Функции нескольких переменных
34.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
1) S0 — начальная сумма вклада,
x — ежегодный процент прироста,
y — количество лет.
Сумма вклада через y лет:
x y
S = S0 1 +
.
100
К.А. Смотрицкий
Функции нескольких переменных
35.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
1) S0 — начальная сумма вклада,
x — ежегодный процент прироста,
y — количество лет.
Сумма вклада через y лет:
x y
S = S0 1 +
.
100
К.А. Смотрицкий
Функции нескольких переменных
36.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
1) S0 — начальная сумма вклада,
x — ежегодный процент прироста,
y — количество лет.
Сумма вклада через y лет:
x y
S = S0 1 +
.
100
К.А. Смотрицкий
Функции нескольких переменных
37.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
1) S0 — начальная сумма вклада,
x — ежегодный процент прироста,
y — количество лет.
Сумма вклада через y лет:
x y
S = S0 1 +
.
100
К.А. Смотрицкий
Функции нескольких переменных
38.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
1) S0 — начальная сумма вклада,
x — ежегодный процент прироста,
y — количество лет.
Сумма вклада через y лет:
x y
S = S0 1 +
.
100
К.А. Смотрицкий
Функции нескольких переменных
39.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
2) Производственная функция (ПФ)
xi — количество i-го фактора.
Величина общественного продукта
y = f (x1 , x2 , . . . , xn ).
ПФ Кобба – Дугласа
x1 — затраты труда, x2 — объем производственных фондов,
a0 , a1 , a2 — некоторые постоянные,
z = a0 xa11 xa22 .
К.А. Смотрицкий
Функции нескольких переменных
40.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
2) Производственная функция (ПФ)
xi — количество i-го фактора.
Величина общественного продукта
y = f (x1 , x2 , . . . , xn ).
ПФ Кобба – Дугласа
x1 — затраты труда, x2 — объем производственных фондов,
a0 , a1 , a2 — некоторые постоянные,
z = a0 xa11 xa22 .
К.А. Смотрицкий
Функции нескольких переменных
41.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
2) Производственная функция (ПФ)
xi — количество i-го фактора.
Величина общественного продукта
y = f (x1 , x2 , . . . , xn ).
ПФ Кобба – Дугласа
x1 — затраты труда, x2 — объем производственных фондов,
a0 , a1 , a2 — некоторые постоянные,
z = a0 xa11 xa22 .
К.А. Смотрицкий
Функции нескольких переменных
42.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
2) Производственная функция (ПФ)
xi — количество i-го фактора.
Величина общественного продукта
y = f (x1 , x2 , . . . , xn ).
ПФ Кобба – Дугласа
x1 — затраты труда, x2 — объем производственных фондов,
a0 , a1 , a2 — некоторые постоянные,
z = a0 xa11 xa22 .
К.А. Смотрицкий
Функции нескольких переменных
43.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
2) Производственная функция (ПФ)
xi — количество i-го фактора.
Величина общественного продукта
y = f (x1 , x2 , . . . , xn ).
ПФ Кобба – Дугласа
x1 — затраты труда, x2 — объем производственных фондов,
a0 , a1 , a2 — некоторые постоянные,
z = a0 xa11 xa22 .
К.А. Смотрицкий
Функции нескольких переменных
44.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
2) Производственная функция (ПФ)
xi — количество i-го фактора.
Величина общественного продукта
y = f (x1 , x2 , . . . , xn ).
ПФ Кобба – Дугласа
x1 — затраты труда, x2 — объем производственных фондов,
a0 , a1 , a2 — некоторые постоянные,
z = a0 xa11 xa22 .
К.А. Смотрицкий
Функции нескольких переменных
45.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
2) Производственная функция (ПФ)
xi — количество i-го фактора.
Величина общественного продукта
y = f (x1 , x2 , . . . , xn ).
ПФ Кобба – Дугласа
x1 — затраты труда, x2 — объем производственных фондов,
a0 , a1 , a2 — некоторые постоянные,
z = a0 xa11 xa22 .
К.А. Смотрицкий
Функции нескольких переменных
46.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
2) Производственная функция (ПФ)
xi — количество i-го фактора.
Величина общественного продукта
y = f (x1 , x2 , . . . , xn ).
ПФ Кобба – Дугласа
x1 — затраты труда, x2 — объем производственных фондов,
a0 , a1 , a2 — некоторые постоянные,
z = a0 xa11 xa22 .
К.А. Смотрицкий
Функции нескольких переменных
47.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
2) Производственная функция (ПФ)
xi — количество i-го фактора.
Величина общественного продукта
y = f (x1 , x2 , . . . , xn ).
ПФ Кобба – Дугласа
x1 — затраты труда, x2 — объем производственных фондов,
a0 , a1 , a2 — некоторые постоянные,
z = a0 xa11 xa22 .
К.А. Смотрицкий
Функции нескольких переменных
48.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
3) Функции спроса на i-тый товар
pi — цена i-го товара, R — доход потребителя,
q = Di (p1 , p2 , . . . , pn , R).
4) Функция полезности набора товаров
xi — количество i-го товара,
u = u(x1 , x2 , . . . , xn ).
К.А. Смотрицкий
Функции нескольких переменных
49.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
3) Функции спроса на i-тый товар
pi — цена i-го товара, R — доход потребителя,
q = Di (p1 , p2 , . . . , pn , R).
4) Функция полезности набора товаров
xi — количество i-го товара,
u = u(x1 , x2 , . . . , xn ).
К.А. Смотрицкий
Функции нескольких переменных
50.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
3) Функции спроса на i-тый товар
pi — цена i-го товара, R — доход потребителя,
q = Di (p1 , p2 , . . . , pn , R).
4) Функция полезности набора товаров
xi — количество i-го товара,
u = u(x1 , x2 , . . . , xn ).
К.А. Смотрицкий
Функции нескольких переменных
51.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
3) Функции спроса на i-тый товар
pi — цена i-го товара, R — доход потребителя,
q = Di (p1 , p2 , . . . , pn , R).
4) Функция полезности набора товаров
xi — количество i-го товара,
u = u(x1 , x2 , . . . , xn ).
К.А. Смотрицкий
Функции нескольких переменных
52.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
3) Функции спроса на i-тый товар
pi — цена i-го товара, R — доход потребителя,
q = Di (p1 , p2 , . . . , pn , R).
4) Функция полезности набора товаров
xi — количество i-го товара,
u = u(x1 , x2 , . . . , xn ).
К.А. Смотрицкий
Функции нескольких переменных
53.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
3) Функции спроса на i-тый товар
pi — цена i-го товара, R — доход потребителя,
q = Di (p1 , p2 , . . . , pn , R).
4) Функция полезности набора товаров
xi — количество i-го товара,
u = u(x1 , x2 , . . . , xn ).
К.А. Смотрицкий
Функции нескольких переменных
54.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
3) Функции спроса на i-тый товар
pi — цена i-го товара, R — доход потребителя,
q = Di (p1 , p2 , . . . , pn , R).
4) Функция полезности набора товаров
xi — количество i-го товара,
u = u(x1 , x2 , . . . , xn ).
К.А. Смотрицкий
Функции нескольких переменных
55.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Примеры функций нескольких переменных,
используемых в экономике
3) Функции спроса на i-тый товар
pi — цена i-го товара, R — доход потребителя,
q = Di (p1 , p2 , . . . , pn , R).
4) Функция полезности набора товаров
xi — количество i-го товара,
u = u(x1 , x2 , . . . , xn ).
К.А. Смотрицкий
Функции нескольких переменных
56.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Геометрическое толкование функции 2-х переменных
Пусть задана функция z = f (x, y), (x, y) ∈ D.
Каждой точке M0 (x0 , y0 ) ∈ D в системе координат Oxyz
поставим в соответствие точку
P (x0 , y0 , z0 ),
где z0 = f (x0 , y0 ) — аппликата точки.
Совокупность всех таких точек представляет собой некоторую
поверхность в трехмерном пространстве, которая называется
графиком функции 2-х переменных.
К.А. Смотрицкий
Функции нескольких переменных
57.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Геометрическое толкование функции 2-х переменных
Пусть задана функция z = f (x, y), (x, y) ∈ D.
Каждой точке M0 (x0 , y0 ) ∈ D в системе координат Oxyz
поставим в соответствие точку
P (x0 , y0 , z0 ),
где z0 = f (x0 , y0 ) — аппликата точки.
Совокупность всех таких точек представляет собой некоторую
поверхность в трехмерном пространстве, которая называется
графиком функции 2-х переменных.
К.А. Смотрицкий
Функции нескольких переменных
58.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Геометрическое толкование функции 2-х переменных
Пусть задана функция z = f (x, y), (x, y) ∈ D.
Каждой точке M0 (x0 , y0 ) ∈ D в системе координат Oxyz
поставим в соответствие точку
P (x0 , y0 , z0 ),
где z0 = f (x0 , y0 ) — аппликата точки.
Совокупность всех таких точек представляет собой некоторую
поверхность в трехмерном пространстве, которая называется
графиком функции 2-х переменных.
К.А. Смотрицкий
Функции нескольких переменных
59.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Геометрическое толкование функции 2-х переменных
Пусть задана функция z = f (x, y), (x, y) ∈ D.
Каждой точке M0 (x0 , y0 ) ∈ D в системе координат Oxyz
поставим в соответствие точку
P (x0 , y0 , z0 ),
где z0 = f (x0 , y0 ) — аппликата точки.
Совокупность всех таких точек представляет собой некоторую
поверхность в трехмерном пространстве, которая называется
графиком функции 2-х переменных.
К.А. Смотрицкий
Функции нескольких переменных
60.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Пример
z=
p
1 − x2 − y 2
К.А. Смотрицкий
Функции нескольких переменных
61.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Пример
z=
p
1 − x2 − y 2
К.А. Смотрицкий
Функции нескольких переменных
62.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Пример
z=
p
1 − x2 − y 2
z
y
x
График функции — некоторая сферическая поверхность.
К.А. Смотрицкий
Функции нескольких переменных
63.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Линией уровня функции 2-х переменных
z = f (x, y)
называется множество точек (x, y) на плоскости Oxy, в
которых функция принимает одно и то же значение, равное C
(C — const).
Число C называется уровнем.
К.А. Смотрицкий
Функции нескольких переменных
64.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Линией уровня функции 2-х переменных
z = f (x, y)
называется множество точек (x, y) на плоскости Oxy, в
которых функция принимает одно и то же значение, равное C
(C — const).
Число C называется уровнем.
К.А. Смотрицкий
Функции нескольких переменных
65.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия
Линией уровня функции 2-х переменных
z = f (x, y)
называется множество точек (x, y) на плоскости Oxy, в
которых функция принимает одно и то же значение, равное C
(C — const).
Число C называется уровнем.
К.А. Смотрицкий
Функции нескольких переменных
66.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Пример
z = x2 + y 2
К.А. Смотрицкий
Функции нескольких переменных
67.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Пример
z = x2 + y 2
К.А. Смотрицкий
Функции нескольких переменных
68.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Пример
z = x2 + y 2
z
y
x
К.А. Смотрицкий
Функции нескольких переменных
69.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Пример
z = x2 + y 2
z
y
x
К.А. Смотрицкий
Функции нескольких переменных
70.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Пример
z = x2 + y 2
z
y
x
К.А. Смотрицкий
Функции нескольких переменных
71.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Пример
z = x2 + y 2
z
y
x
К.А. Смотрицкий
Функции нескольких переменных
72.
Основные понятия Предел функции Непрерывность функции Частные производные1. Основные понятия.
Пример
z = x2 + y 2
z
y
x
К.А. Смотрицкий
Функции нескольких переменных
73.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции
Множество всех точек M (x, y)
плоскости, координаты которых
удовлетворяют неравенству
(x − x0 )2 + (y − y0 )2 < δ 2 ,
называется δ-окрестностью
точки M0 (x0 , y0 ).
К.А. Смотрицкий
Функции нескольких переменных
74.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции
Множество всех точек M (x, y)
плоскости, координаты которых
удовлетворяют неравенству
(x − x0 )2 + (y − y0 )2 < δ 2 ,
называется δ-окрестностью
точки M0 (x0 , y0 ).
К.А. Смотрицкий
Функции нескольких переменных
75.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции
Множество всех точек M (x, y)
плоскости, координаты которых
удовлетворяют неравенству
y
(x − x0 )2 + (y − y − 0)2 < δ 2 ,
y0
δ
b
M0
называется δ-окрестностью
точки M0 (x0 , y0 ).
δ-окрестность точки
M0 (x0 , y0 )— круг с центром в
точке (x0 , y0 ) радиуса δ.
К.А. Смотрицкий
x0
Функции нескольких переменных
x
76.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции
Множество всех точек M (x, y)
плоскости, координаты которых
удовлетворяют неравенству
y
(x − x0 )2 + (y − y − 0)2 < δ 2 ,
y0
δ
b
M0
называется δ-окрестностью
точки M0 (x0 , y0 ).
δ-окрестность точки
M0 (x0 , y0 )— круг с центром в
точке (x0 , y0 ) радиуса δ.
К.А. Смотрицкий
x0
Функции нескольких переменных
x
77.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Предел функции на языке «ε − δ» (по Коши)
Число A называется пределом функции z = f (x, y) в точке
M0 (x0 , y0 ), если для любого числа ε > 0 существует такое
число δ > 0, зависящее от ε, что для всех (x, y),
удовлетворяющих условию
0 < (x − x0 )2 + (y − y0 )2 < δ 2 ,
выполняется неравенство
|f (x, y) − A| < ε.
К.А. Смотрицкий
Функции нескольких переменных
78.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Предел функции на языке «ε − δ» (по Коши)
Число A называется пределом функции z = f (x, y) в точке
M0 (x0 , y0 ), если для любого числа ε > 0 существует такое
число δ > 0, зависящее от ε, что для всех (x, y),
удовлетворяющих условию
0 < (x − x0 )2 + (y − y0 )2 < δ 2 ,
выполняется неравенство
|f (x, y) − A| < ε.
К.А. Смотрицкий
Функции нескольких переменных
79.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Предел функции на языке «ε − δ» (по Коши)
Число A называется пределом функции z = f (x, y) в точке
M0 (x0 , y0 ), если для любого числа ε > 0 существует такое
число δ > 0, зависящее от ε, что для всех (x, y),
удовлетворяющих условию
0 < (x − x0 )2 + (y − y0 )2 < δ 2 ,
выполняется неравенство
|f (x, y) − A| < ε.
К.А. Смотрицкий
Функции нескольких переменных
80.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Предел функции на языке «ε − δ» (по Коши)
Число A называется пределом функции z = f (x, y) в точке
M0 (x0 , y0 ), если для любого числа ε > 0 существует такое
число δ > 0, зависящее от ε, что для всех (x, y),
удовлетворяющих условию
0 < (x − x0 )2 + (y − y0 )2 < δ 2 ,
выполняется неравенство
|f (x, y) − A| < ε.
К.А. Смотрицкий
Функции нескольких переменных
81.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Предел функции на языке «ε − δ» (по Коши)
Число A называется пределом функции z = f (x, y) в точке
M0 (x0 , y0 ), если для любого числа ε > 0 существует такое
число δ > 0, зависящее от ε, что для всех (x, y),
удовлетворяющих условию
0 < (x − x0 )2 + (y − y0 )2 < δ 2 ,
выполняется неравенство
|f (x, y) − A| < ε.
К.А. Смотрицкий
Функции нескольких переменных
82.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Предел функции на языке «ε − δ» (по Коши)
lim f (x, y) = A
M →M0
⇔
∀ε > 0 ∃δ = δ(ε) > 0
∀ (x, y) : 0 < (x − x0 )2 + (y − y0 )2 < δ 2
|f (x, y) − A| < ε.
К.А. Смотрицкий
Функции нескольких переменных
83.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Предел функции на языке «ε − δ» (по Коши)
lim f (x, y) = A
M →M0
⇔
∀ε > 0 ∃δ = δ(ε) > 0
∀ (x, y) : 0 < (x − x0 )2 + (y − y0 )2 < δ 2
|f (x, y) − A| < ε.
К.А. Смотрицкий
Функции нескольких переменных
84.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Предел функции на языке «ε − δ» (по Коши)
lim f (x, y) = A
M →M0
⇔
∀ε > 0 ∃δ = δ(ε) > 0
∀ (x, y) : 0 < (x − x0 )2 + (y − y0 )2 < δ 2
|f (x, y) − A| < ε.
К.А. Смотрицкий
Функции нескольких переменных
85.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Предел функции на языке «ε − δ» (по Коши)
lim f (x, y) = A
M →M0
⇔
∀ε > 0 ∃δ = δ(ε) > 0
∀ (x, y) : 0 < (x − x0 )2 + (y − y0 )2 < δ 2
|f (x, y) − A| < ε.
К.А. Смотрицкий
Функции нескольких переменных
86.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Предел функции на языке «ε − δ» (по Коши)
lim f (x, y) = A
M →M0
⇔
∀ε > 0 ∃δ = δ(ε) > 0
∀ (x, y) : 0 < (x − x0 )2 + (y − y0 )2 < δ 2
|f (x, y) − A| < ε.
К.А. Смотрицкий
Функции нескольких переменных
87.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Геометрический смысл предела функции
Каково бы ни было ε > 0, найдется δ-окрестность точки
M0 (x0 , y0 ), что во всех точках M (x, y), отличных от M0 ,
аппликаты соответствующих точек поверхности z = f (x, y)
отличаются от числа A по модулю меньше, чем на ε.
К.А. Смотрицкий
Функции нескольких переменных
88.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Геометрический смысл предела функции
Каково бы ни было ε > 0, найдется δ-окрестность точки
M0 (x0 , y0 ), что во всех точках M (x, y), отличных от M0 ,
аппликаты соответствующих точек поверхности z = f (x, y)
отличаются от числа A по модулю меньше, чем на ε.
К.А. Смотрицкий
Функции нескольких переменных
89.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Геометрический смысл предела функции
Каково бы ни было ε > 0, найдется δ-окрестность точки
M0 (x0 , y0 ), что во всех точках M (x, y), отличных от M0 ,
аппликаты соответствующих точек поверхности z = f (x, y)
отличаются от числа A по модулю меньше, чем на ε.
y
y0
z
b
x0
К.А. Смотрицкий
A
x
Функции нескольких переменных
90.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Геометрический смысл предела функции
Каково бы ни было ε > 0, найдется δ-окрестность точки
M0 (x0 , y0 ), что во всех точках M (x, y), отличных от M0 ,
аппликаты соответствующих точек поверхности z = f (x, y)
отличаются от числа A по модулю меньше, чем на ε.
y
z
A+ε
y0
b
x0
К.А. Смотрицкий
A
x
A−ε
Функции нескольких переменных
91.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Геометрический смысл предела функции
Каково бы ни было ε > 0, найдется δ-окрестность точки
M0 (x0 , y0 ), что во всех точках M (x, y), отличных от M0 ,
аппликаты соответствующих точек поверхности z = f (x, y)
отличаются от числа A по модулю меньше, чем на ε.
y
z
A+ε
δ
y0
b
x0
К.А. Смотрицкий
A
x
A−ε
Функции нескольких переменных
92.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Геометрический смысл предела функции
Каково бы ни было ε > 0, найдется δ-окрестность точки
M0 (x0 , y0 ), что во всех точках M (x, y), отличных от M0 ,
аппликаты соответствующих точек поверхности z = f (x, y)
отличаются от числа A по модулю меньше, чем на ε.
y
z
δ
y0
b
A+ε
b
M
x0
К.А. Смотрицкий
A
x
A−ε
Функции нескольких переменных
93.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Геометрический смысл предела функции
Каково бы ни было ε > 0, найдется δ-окрестность точки
M0 (x0 , y0 ), что во всех точках M (x, y), отличных от M0 ,
аппликаты соответствующих точек поверхности z = f (x, y)
отличаются от числа A по модулю меньше, чем на ε.
y
z
δ
y0
b
A+ε
b
M
x0
К.А. Смотрицкий
f (M )
A
x
A−ε
Функции нескольких переменных
94.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции
Для предела функции одной переменной существуют два
направления — предел слева и предел справа:
lim f (x),
lim f (x).
x→x0 −0
x→x0 +0
К.А. Смотрицкий
Функции нескольких переменных
95.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции
Для предела функции одной переменной существуют два
направления — предел слева и предел справа:
lim f (x),
lim f (x).
x→x0 −0
x→x0 +0
К.А. Смотрицкий
Функции нескольких переменных
96.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции
Для предела функции одной переменной существуют два
направления — предел слева и предел справа:
lim f (x),
lim f (x).
x→x0 −0
x→x0 +0
К.А. Смотрицкий
Функции нескольких переменных
97.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции
Для предела функции одной переменной существуют два
направления — предел слева и предел справа:
lim f (x),
lim f (x).
x→x0 −0
x→x0 +0
b
x0
К.А. Смотрицкий
Функции нескольких переменных
98.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции
На плоскости в окрестности каждой точки (x0 , y0 ) таких
направлений бесконечно много и по каждому из них предел
функции должен существовать и все эти пределы должны быть
равны между собой.
Только в этом случае будет существовать предел
lim f (x, y).
M →M0
К.А. Смотрицкий
Функции нескольких переменных
99.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции
На плоскости в окрестности каждой точки (x0 , y0 ) таких
направлений бесконечно много и по каждому из них предел
функции должен существовать и все эти пределы должны быть
равны между собой.
Только в этом случае будет существовать предел
lim f (x, y).
M →M0
К.А. Смотрицкий
Функции нескольких переменных
100.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции
На плоскости в окрестности каждой точки (x0 , y0 ) таких
направлений бесконечно много и по каждому из них предел
функции должен существовать и все эти пределы должны быть
равны между собой.
Только в этом случае будет существовать предел
lim f (x, y).
M →M0
К.А. Смотрицкий
Функции нескольких переменных
101.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
lim
2x − y
(x,y)→(0,0) 2x + y
.
Будем приближаться к точке O(0, 0) по прямой y = kx, где k —
некоторое фиксированное число.
Тогда
2x − kx
2−k
2x − y
= lim
=
.
lim
x→0 2x + kx
2+k
(x,y)→(0,0) 2x + y
При различных k получим разные значения.
2x−y
Следовательно, предел функции z = 2x+y
в точке O(0, 0) не
существует.
К.А. Смотрицкий
Функции нескольких переменных
102.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
lim
2x − y
(x,y)→(0,0) 2x + y
.
Будем приближаться к точке O(0, 0) по прямой y = kx, где k —
некоторое фиксированное число.
Тогда
2x − kx
2−k
2x − y
= lim
=
.
lim
x→0 2x + kx
2+k
(x,y)→(0,0) 2x + y
При различных k получим разные значения.
Следовательно, предел функции z = 2x−y
2x+y в точке O(0, 0) не
существует.
К.А. Смотрицкий
Функции нескольких переменных
103.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
lim
2x − y
(x,y)→(0,0) 2x + y
.
Будем приближаться к точке O(0, 0) по прямой y = kx, где k —
некоторое фиксированное число.
Тогда
2x − kx
2x − y
2−k
lim
= lim
=
.
x→0 2x + kx
2+k
(x,y)→(0,0) 2x + y
При различных k получим разные значения.
Следовательно, предел функции z = 2x−y
2x+y в точке O(0, 0) не
существует.
К.А. Смотрицкий
Функции нескольких переменных
104.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
lim
2x − y
(x,y)→(0,0) 2x + y
.
Будем приближаться к точке O(0, 0) по прямой y = kx, где k —
некоторое фиксированное число.
Тогда
2x − kx
2−k
2x − y
=
.
lim
= lim
x→0 2x + kx
2+k
(x,y)→(0,0) 2x + y
При различных k получим разные значения.
Следовательно, предел функции z = 2x−y
2x+y в точке O(0, 0) не
существует.
К.А. Смотрицкий
Функции нескольких переменных
105.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
lim
2x − y
(x,y)→(0,0) 2x + y
.
Будем приближаться к точке O(0, 0) по прямой y = kx, где k —
некоторое фиксированное число.
Тогда
2x − kx
2−k
2x − y
=
.
lim
= lim
x→0 2x + kx
2+k
(x,y)→(0,0) 2x + y
При различных k получим разные значения.
Следовательно, предел функции z = 2x−y
2x+y в точке O(0, 0) не
существует.
К.А. Смотрицкий
Функции нескольких переменных
106.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
lim
2x − y
(x,y)→(0,0) 2x + y
.
Будем приближаться к точке O(0, 0) по прямой y = kx, где k —
некоторое фиксированное число.
Тогда
2x − kx
2−k
2x − y
=
.
lim
= lim
x→0 2x + kx
2+k
(x,y)→(0,0) 2x + y
При различных k получим разные значения.
Следовательно, предел функции z = 2x−y
2x+y в точке O(0, 0) не
существует.
К.А. Смотрицкий
Функции нескольких переменных
107.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
lim
2x − y
(x,y)→(0,0) 2x + y
.
Будем приближаться к точке O(0, 0) по прямой y = kx, где k —
некоторое фиксированное число.
Тогда
2x − kx
2−k
2x − y
=
.
lim
= lim
x→0 2x + kx
2+k
(x,y)→(0,0) 2x + y
При различных k получим разные значения.
2x−y
Следовательно, предел функции z = 2x+y
в точке O(0, 0) не
существует.
К.А. Смотрицкий
Функции нескольких переменных
108.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
lim
2x − y
(x,y)→(0,0) 2x + y
.
Будем приближаться к точке O(0, 0) по прямой y = kx, где k —
некоторое фиксированное число.
Тогда
2x − kx
2−k
2x − y
=
.
lim
= lim
x→0 2x + kx
2+k
(x,y)→(0,0) 2x + y
При различных k получим разные значения.
2x−y
Следовательно, предел функции z = 2x+y
в точке O(0, 0) не
существует.
К.А. Смотрицкий
Функции нескольких переменных
109.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
sin(x2 + y 2 )
.
x2 + y 2
(x,y)→(0,0)
lim
Обозначим x2 + y 2 = ρ.
Тогда
sin ρ
sin(x2 + y 2 )
= lim
= 1.
lim
2
2
ρ→0 ρ
x +y
(x,y)→(0,0)
К.А. Смотрицкий
Функции нескольких переменных
110.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
sin(x2 + y 2 )
.
x2 + y 2
(x,y)→(0,0)
lim
Обозначим x2 + y 2 = ρ.
Тогда
sin ρ
sin(x2 + y 2 )
= lim
= 1.
lim
2
2
ρ→0 ρ
x +y
(x,y)→(0,0)
К.А. Смотрицкий
Функции нескольких переменных
111.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
sin(x2 + y 2 )
.
x2 + y 2
(x,y)→(0,0)
lim
Обозначим x2 + y 2 = ρ.
Тогда
sin ρ
sin(x2 + y 2 )
lim
= lim
= 1.
2
2
ρ→0 ρ
x +y
(x,y)→(0,0)
К.А. Смотрицкий
Функции нескольких переменных
112.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
sin(x2 + y 2 )
.
x2 + y 2
(x,y)→(0,0)
lim
Обозначим x2 + y 2 = ρ.
Тогда
sin ρ
sin(x2 + y 2 )
= 1.
lim
= lim
2
2
ρ→0 ρ
x +y
(x,y)→(0,0)
К.А. Смотрицкий
Функции нескольких переменных
113.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
sin(x2 + y 2 )
.
x2 + y 2
(x,y)→(0,0)
lim
Обозначим x2 + y 2 = ρ.
Тогда
sin ρ
sin(x2 + y 2 )
= 1.
lim
= lim
2
2
ρ→0 ρ
x +y
(x,y)→(0,0)
К.А. Смотрицкий
Функции нескольких переменных
114.
Основные понятия Предел функции Непрерывность функции Частные производные2. Предел функции.
Пример
Найти предел
sin(x2 + y 2 )
.
x2 + y 2
(x,y)→(0,0)
lim
Обозначим x2 + y 2 = ρ.
Тогда
sin ρ
sin(x2 + y 2 )
= 1.
lim
= lim
2
2
ρ→0 ρ
x +y
(x,y)→(0,0)
К.А. Смотрицкий
Функции нескольких переменных
115.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
Функция z = f (x, y) называется непрерывной в точке
M0 (x0 , y0 ), если существует предел функции в этой точке и он
равен значению функции в этой точке:
lim f (x, y) = f (M0 ).
M →M0
К.А. Смотрицкий
Функции нескольких переменных
116.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
Функция z = f (x, y) называется непрерывной в точке
M0 (x0 , y0 ), если существует предел функции в этой точке и он
равен значению функции в этой точке:
lim f (x, y) = f (M0 ).
M →M0
К.А. Смотрицкий
Функции нескольких переменных
117.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
Функция z = f (x, y) называется непрерывной в точке
M0 (x0 , y0 ), если существует предел функции в этой точке и он
равен значению функции в этой точке:
lim f (x, y) = f (M0 ).
M →M0
К.А. Смотрицкий
Функции нескольких переменных
118.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
∆x = x − x0 ,
— приращения аргументов,
∆y = y − y0
∆z = f (x, y) − f (x0 , y0 ) = f (x0 + ∆x, y0 + ∆y) − f (x0 , y0 ) —
полное приращение функции в точке M0 (x0 , y0 ).
Функция z = f (x, y) называется непрерывной в точке
M0 (x0 , y0 ), если
lim ∆z = 0.
∆x→0
∆y→0
К.А. Смотрицкий
Функции нескольких переменных
119.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
∆x = x − x0 ,
— приращения аргументов,
∆y = y − y0
∆z = f (x, y) − f (x0 , y0 ) = f (x0 + ∆x, y0 + ∆y) − f (x0 , y0 ) —
полное приращение функции в точке M0 (x0 , y0 ).
Функция z = f (x, y) называется непрерывной в точке
M0 (x0 , y0 ), если
lim ∆z = 0.
∆x→0
∆y→0
К.А. Смотрицкий
Функции нескольких переменных
120.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
∆x = x − x0 ,
— приращения аргументов,
∆y = y − y0
∆z = f (x, y) − f (x0 , y0 ) = f (x0 + ∆x, y0 + ∆y) − f (x0 , y0 ) —
полное приращение функции в точке M0 (x0 , y0 ).
Функция z = f (x, y) называется непрерывной в точке
M0 (x0 , y0 ), если
lim ∆z = 0.
∆x→0
∆y→0
К.А. Смотрицкий
Функции нескольких переменных
121.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
∆x = x − x0 ,
— приращения аргументов,
∆y = y − y0
∆z = f (x, y) − f (x0 , y0 ) = f (x0 + ∆x, y0 + ∆y) − f (x0 , y0 ) —
полное приращение функции в точке M0 (x0 , y0 ).
Функция z = f (x, y) называется непрерывной в точке
M0 (x0 , y0 ), если
lim ∆z = 0.
∆x→0
∆y→0
К.А. Смотрицкий
Функции нескольких переменных
122.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
∆x = x − x0 ,
— приращения аргументов,
∆y = y − y0
∆z = f (x, y) − f (x0 , y0 ) = f (x0 + ∆x, y0 + ∆y) − f (x0 , y0 ) —
полное приращение функции в точке M0 (x0 , y0 ).
Функция z = f (x, y) называется непрерывной в точке
M0 (x0 , y0 ), если
lim ∆z = 0.
∆x→0
∆y→0
К.А. Смотрицкий
Функции нескольких переменных
123.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
lim
∆z = 0
∆x→0
∆y→0
⇔
∀ε > 0 ∃δ = δ(ε) > 0 ∀|∆x| < δ
|∆z| < ε.
∀|∆y| < δ
Функция z = f (x, y) является непрерывной в точке M0 , если ее
полное приращение есть бесконечно малая величина при
M → M0 .
К.А. Смотрицкий
Функции нескольких переменных
124.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
lim
∆z = 0
∆x→0
∆y→0
⇔
∀ε > 0 ∃δ = δ(ε) > 0 ∀|∆x| < δ
|∆z| < ε.
∀|∆y| < δ
Функция z = f (x, y) является непрерывной в точке M0 , если ее
полное приращение есть бесконечно малая величина при
M → M0 .
К.А. Смотрицкий
Функции нескольких переменных
125.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
lim
∆z = 0
∆x→0
∆y→0
⇔
∀ε > 0 ∃δ = δ(ε) > 0 ∀|∆x| < δ
|∆z| < ε.
∀|∆y| < δ
Функция z = f (x, y) является непрерывной в точке M0 , если ее
полное приращение есть бесконечно малая величина при
M → M0 .
К.А. Смотрицкий
Функции нескольких переменных
126.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
lim
∆z = 0
∆x→0
∆y→0
⇔
∀ε > 0 ∃δ = δ(ε) > 0 ∀|∆x| < δ
|∆z| < ε.
∀|∆y| < δ
Функция z = f (x, y) является непрерывной в точке M0 , если ее
полное приращение есть бесконечно малая величина при
M → M0 .
К.А. Смотрицкий
Функции нескольких переменных
127.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
Точками разрыва функции z = f (x, y) называются те точки, в
которых функция z = f (x, y) не является непрерывной.
К.А. Смотрицкий
Функции нескольких переменных
128.
Основные понятия Предел функции Непрерывность функции Частные производные3. Непрерывность функции
Точками разрыва функции z = f (x, y) называются те точки, в
которых функция z = f (x, y) не является непрерывной.
К.А. Смотрицкий
Функции нескольких переменных
129.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Пусть функция z = f (x, y) определена в некоторой окрестности
точки M (x, y).
∆z = f (x + ∆x, y + ∆y) − f (x, y)
— полное приращение функции.
Полагая здесь ∆y = 0, получаем
∆x z = f (x + ∆x, y) − f (x, y)
— частное приращение функции по x.
К.А. Смотрицкий
Функции нескольких переменных
130.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Пусть функция z = f (x, y) определена в некоторой окрестности
точки M (x, y).
∆z = f (x + ∆x, y + ∆y) − f (x, y)
— полное приращение функции.
Полагая здесь ∆y = 0, получаем
∆x z = f (x + ∆x, y) − f (x, y)
— частное приращение функции по x.
К.А. Смотрицкий
Функции нескольких переменных
131.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Пусть функция z = f (x, y) определена в некоторой окрестности
точки M (x, y).
∆z = f (x + ∆x, y + ∆y) − f (x, y)
— полное приращение функции.
Полагая здесь ∆y = 0, получаем
∆x z = f (x + ∆x, y) − f (x, y)
— частное приращение функции по x.
К.А. Смотрицкий
Функции нескольких переменных
132.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Пусть функция z = f (x, y) определена в некоторой окрестности
точки M (x, y).
∆z = f (x + ∆x, y + ∆y) − f (x, y)
— полное приращение функции.
Полагая здесь ∆y = 0, получаем
∆x z = f (x + ∆x, y) − f (x, y)
— частное приращение функции по x.
К.А. Смотрицкий
Функции нескольких переменных
133.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Пусть функция z = f (x, y) определена в некоторой окрестности
точки M (x, y).
∆z = f (x + ∆x, y + ∆y) − f (x, y)
— полное приращение функции.
Полагая здесь ∆y = 0, получаем
∆x z = f (x + ∆x, y) − f (x, y)
— частное приращение функции по x.
К.А. Смотрицкий
Функции нескольких переменных
134.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Если существует предел
f (x + ∆x, y) − f (x, y)
,
∆x→0
∆x
lim
то он называется частной производной функции f в точке
M (x, y) по переменной x и обозначается
∂z
,
∂x
∂f
,
∂x
zx0 ,
fx0 .
∂z
f (x + ∆x, y) − f (x, y)
= lim
.
∂x ∆x→0
∆x
К.А. Смотрицкий
Функции нескольких переменных
135.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Если существует предел
f (x + ∆x, y) − f (x, y)
,
∆x→0
∆x
lim
то он называется частной производной функции f в точке
M (x, y) по переменной x и обозначается
∂z
,
∂x
∂f
,
∂x
zx0 ,
fx0 .
∂z
f (x + ∆x, y) − f (x, y)
= lim
.
∂x ∆x→0
∆x
К.А. Смотрицкий
Функции нескольких переменных
136.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Если существует предел
f (x + ∆x, y) − f (x, y)
,
∆x→0
∆x
lim
то он называется частной производной функции f в точке
M (x, y) по переменной x и обозначается
∂z
,
∂x
∂f
,
∂x
zx0 ,
fx0 .
f (x + ∆x, y) − f (x, y)
∂z
= lim
.
∂x ∆x→0
∆x
К.А. Смотрицкий
Функции нескольких переменных
137.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Если существует предел
f (x + ∆x, y) − f (x, y)
,
∆x→0
∆x
lim
то он называется частной производной функции f в точке
M (x, y) по переменной x и обозначается
∂z
,
∂x
∂f
,
∂x
zx0 ,
fx0 .
f (x + ∆x, y) − f (x, y)
∂z
= lim
.
∂x ∆x→0
∆x
К.А. Смотрицкий
Функции нескольких переменных
138.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
∆z = f (x + ∆x, y + ∆y) − f (x, y).
Полагая здесь ∆x = 0, получаем
∆y z = f (x, y + ∆y) − f (x, y)
– частное приращение функции по y.
К.А. Смотрицкий
Функции нескольких переменных
139.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
∆z = f (x + ∆x, y + ∆y) − f (x, y).
Полагая здесь ∆x = 0, получаем
∆y z = f (x, y + ∆y) − f (x, y)
– частное приращение функции по y.
К.А. Смотрицкий
Функции нескольких переменных
140.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
∆z = f (x + ∆x, y + ∆y) − f (x, y).
Полагая здесь ∆x = 0, получаем
∆y z = f (x, y + ∆y) − f (x, y)
– частное приращение функции по y.
К.А. Смотрицкий
Функции нескольких переменных
141.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
∆z = f (x + ∆x, y + ∆y) − f (x, y).
Полагая здесь ∆x = 0, получаем
∆y z = f (x, y + ∆y) − f (x, y)
– частное приращение функции по y.
К.А. Смотрицкий
Функции нескольких переменных
142.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Если существует предел
f (x, y + ∆y) − f (x, y)
,
∆y→0
∆y
lim
то он называется частной производной функции f в точке
M (x, y) по переменной y и обозначается
∂z
,
∂y
∂f
,
∂y
zy0 ,
fy0 .
∂z
f (x, y + ∆y) − f (x, y)
= lim
.
∂y ∆y→0
∆y
К.А. Смотрицкий
Функции нескольких переменных
143.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Если существует предел
f (x, y + ∆y) − f (x, y)
,
∆y→0
∆y
lim
то он называется частной производной функции f в точке
M (x, y) по переменной y и обозначается
∂z
,
∂y
∂f
,
∂y
zy0 ,
fy0 .
∂z
f (x, y + ∆y) − f (x, y)
= lim
.
∂y ∆y→0
∆y
К.А. Смотрицкий
Функции нескольких переменных
144.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Если существует предел
f (x, y + ∆y) − f (x, y)
,
∆y→0
∆y
lim
то он называется частной производной функции f в точке
M (x, y) по переменной y и обозначается
∂z
,
∂y
∂f
,
∂y
zy0 ,
fy0 .
∂z
f (x, y + ∆y) − f (x, y)
= lim
.
∂y ∆y→0
∆y
К.А. Смотрицкий
Функции нескольких переменных
145.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные
Если существует предел
f (x, y + ∆y) − f (x, y)
,
∆y→0
∆y
lim
то он называется частной производной функции f в точке
M (x, y) по переменной y и обозначается
∂z
,
∂y
∂f
,
∂y
zy0 ,
fy0 .
∂z
f (x, y + ∆y) − f (x, y)
= lim
.
∂y ∆y→0
∆y
К.А. Смотрицкий
Функции нескольких переменных
146.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Замечание
Частная производная функции двух переменных равна обычной
производной функции одной переменной, полученной при
условии, что вторая переменная сохраняет постоянное
значение.
К.А. Смотрицкий
Функции нескольких переменных
147.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Замечание
Частная производная функции двух переменных равна обычной
производной функции одной переменной, полученной при
условии, что вторая переменная сохраняет постоянное
значение.
К.А. Смотрицкий
Функции нескольких переменных
148.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
149.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
150.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
151.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
152.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
153.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
154.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
155.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
156.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
157.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
158.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
159.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
160.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
1) z = 2x3 + 5y 2 − 3xy 4 + 6x + y.
∂z
= 6x2 + 0 − 3y 4 + 6 + 0,
∂x
∂z
= 0 + 10y − 3x · 4y 3 + 0 + 1.
∂y
К.А. Смотрицкий
Функции нескольких переменных
161.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
2) z = arctg(3x2 y + 1).
∂z
1
=
· 6xy,
∂x
1 + (3x2 y + 1)2
∂z
1
=
· 3x2 .
∂y
1 + (3x2 y + 1)2
К.А. Смотрицкий
Функции нескольких переменных
162.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
2) z = arctg(3x2 y + 1).
∂z
1
=
· 6xy,
∂x
1 + (3x2 y + 1)2
∂z
1
=
· 3x2 .
∂y
1 + (3x2 y + 1)2
К.А. Смотрицкий
Функции нескольких переменных
163.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
2) z = arctg(3x2 y + 1).
∂z
1
=
· 6xy,
∂x
1 + (3x2 y + 1)2
∂z
1
=
· 3x2 .
∂y
1 + (3x2 y + 1)2
К.А. Смотрицкий
Функции нескольких переменных
164.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
2) z = arctg(3x2 y + 1).
∂z
1
=
· 6xy,
∂x
1 + (3x2 y + 1)2
∂z
1
=
· 3x2 .
∂y
1 + (3x2 y + 1)2
К.А. Смотрицкий
Функции нескольких переменных
165.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
2) z = arctg(3x2 y + 1).
∂z
1
=
· 6xy,
∂x
1 + (3x2 y + 1)2
∂z
1
=
· 3x2 .
∂y
1 + (3x2 y + 1)2
К.А. Смотрицкий
Функции нескольких переменных
166.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
2) z = arctg(3x2 y + 1).
∂z
1
=
· 6xy,
∂x
1 + (3x2 y + 1)2
∂z
1
=
· 3x2 .
∂y
1 + (3x2 y + 1)2
К.А. Смотрицкий
Функции нескольких переменных
167.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
2) z = arctg(3x2 y + 1).
∂z
1
=
· 6xy,
∂x
1 + (3x2 y + 1)2
∂z
1
=
· 3x2 .
∂y
1 + (3x2 y + 1)2
К.А. Смотрицкий
Функции нескольких переменных
168.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
√
3) u = zx3 + x4 y 2 + 3 zy 4 + 2z + 7y.
∂u
= z · 3x2 + y 2 · 4x3 + 0 + 0 + 0,
∂x
√
∂u
= 0 + x4 · 2y + 3 z · 4y 3 + 0 + 7,
∂y
∂u
1
= x3 · 1 + 0 + 3y 4 · √ + 2 + 0.
∂z
2 z
К.А. Смотрицкий
Функции нескольких переменных
169.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
√
3) u = zx3 + x4 y 2 + 3 zy 4 + 2z + 7y.
∂u
= z · 3x2 + y 2 · 4x3 + 0 + 0 + 0,
∂x
√
∂u
= 0 + x4 · 2y + 3 z · 4y 3 + 0 + 7,
∂y
∂u
1
= x3 · 1 + 0 + 3y 4 · √ + 2 + 0.
∂z
2 z
К.А. Смотрицкий
Функции нескольких переменных
170.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
√
3) u = zx3 + x4 y 2 + 3 zy 4 + 2z + 7y.
∂u
= z · 3x2 + y 2 · 4x3 + 0 + 0 + 0,
∂x
√
∂u
= 0 + x4 · 2y + 3 z · 4y 3 + 0 + 7,
∂y
∂u
1
= x3 · 1 + 0 + 3y 4 · √ + 2 + 0.
∂z
2 z
К.А. Смотрицкий
Функции нескольких переменных
171.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
√
3) u = zx3 + x4 y 2 + 3 zy 4 + 2z + 7y.
∂u
= z · 3x2 + y 2 · 4x3 + 0 + 0 + 0,
∂x
√
∂u
= 0 + x4 · 2y + 3 z · 4y 3 + 0 + 7,
∂y
∂u
1
= x3 · 1 + 0 + 3y 4 · √ + 2 + 0.
∂z
2 z
К.А. Смотрицкий
Функции нескольких переменных
172.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
√
3) u = zx3 + x4 y 2 + 3 zy 4 + 2z + 7y.
∂u
= z · 3x2 + y 2 · 4x3 + 0 + 0 + 0,
∂x
√
∂u
= 0 + x4 · 2y + 3 z · 4y 3 + 0 + 7,
∂y
∂u
1
= x3 · 1 + 0 + 3y 4 · √ + 2 + 0.
∂z
2 z
К.А. Смотрицкий
Функции нескольких переменных
173.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
√
3) u = zx3 + x4 y 2 + 3 zy 4 + 2z + 7y.
∂u
= z · 3x2 + y 2 · 4x3 + 0 + 0 + 0,
∂x
√
∂u
= 0 + x4 · 2y + 3 z · 4y 3 + 0 + 7,
∂y
∂u
1
= x3 · 1 + 0 + 3y 4 · √ + 2 + 0.
∂z
2 z
К.А. Смотрицкий
Функции нескольких переменных
174.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
4) F (K, L) = aK α L1−α , α ∈ (0, 1).
1−α
∂F
L
1−α
α−1
= aL
· αK
= aα ·
,
∂K
K
α
∂F
K
= aK α · (1 − α)L−α = a(1 − α) ·
.
∂L
L
К.А. Смотрицкий
Функции нескольких переменных
175.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
4) F (K, L) = aK α L1−α , α ∈ (0, 1).
1−α
∂F
L
1−α
α−1
= aL
· αK
= aα ·
,
∂K
K
α
K
∂F
= aK α · (1 − α)L−α = a(1 − α) ·
.
∂L
L
К.А. Смотрицкий
Функции нескольких переменных
176.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
4) F (K, L) = aK α L1−α , α ∈ (0, 1).
1−α
∂F
L
1−α
α−1
= aL
· αK
= aα ·
,
∂K
K
α
∂F
K
= aK α · (1 − α)L−α = a(1 − α) ·
.
∂L
L
К.А. Смотрицкий
Функции нескольких переменных
177.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
4) F (K, L) = aK α L1−α , α ∈ (0, 1).
1−α
∂F
L
1−α
α−1
= aL
· αK
= aα ·
,
∂K
K
α
K
∂F
.
= aK α · (1 − α)L−α = a(1 − α) ·
L
∂L
К.А. Смотрицкий
Функции нескольких переменных
178.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Примеры
4) F (K, L) = aK α L1−α , α ∈ (0, 1).
1−α
∂F
L
1−α
α−1
= aL
· αK
= aα ·
,
∂K
K
α
K
∂F
.
= aK α · (1 − α)L−α = a(1 − α) ·
L
∂L
К.А. Смотрицкий
Функции нескольких переменных
179.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Геометрический смысл частных производных
∂z(x0 , y0 )
= tg α
∂x
α — угол между осью Ox и
касательной, проведенной в
точке M0 (x0 , y0 , f (x0 , y0 )) к
кривой, являющейся
пересечением поверхности
z = f (x, y) с плоскостью
y = y0 .
К.А. Смотрицкий
Функции нескольких переменных
180.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Геометрический смысл частных производных
∂z(x0 , y0 )
= tg α
∂x
α — угол между осью Ox и
касательной, проведенной в
точке M0 (x0 , y0 , f (x0 , y0 )) к
кривой, являющейся
пересечением поверхности
z = f (x, y) с плоскостью
y = y0 .
К.А. Смотрицкий
Функции нескольких переменных
181.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Геометрический смысл частных производных
∂z(x0 , y0 )
= tg α
∂x
α — угол между осью Ox и
касательной, проведенной в
точке M0 (x0 , y0 , f (x0 , y0 )) к
кривой, являющейся
пересечением поверхности
z = f (x, y) с плоскостью
y = y0 .
К.А. Смотрицкий
Функции нескольких переменных
182.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Геометрический смысл частных производных
∂z(x0 , y0 )
= tg α
∂x
α — угол между осью Ox и
касательной, проведенной в
точке M0 (x0 , y0 , f (x0 , y0 )) к
кривой, являющейся
пересечением поверхности
z = f (x, y) с плоскостью
y = y0 .
z
M0
b
y
x0
x
К.А. Смотрицкий
Функции нескольких переменных
y0
183.
Основные понятия Предел функции Непрерывность функции Частные производные4. Частные производные.
Геометрический смысл частных производных
∂z(x0 , y0 )
= tg α
∂x
α — угол между осью Ox и
касательной, проведенной в
точке M0 (x0 , y0 , f (x0 , y0 )) к
кривой, являющейся
пересечением поверхности
z = f (x, y) с плоскостью
y = y0 .
z
M0
b
y
x0
x
α
К.А. Смотрицкий
Функции нескольких переменных
y0

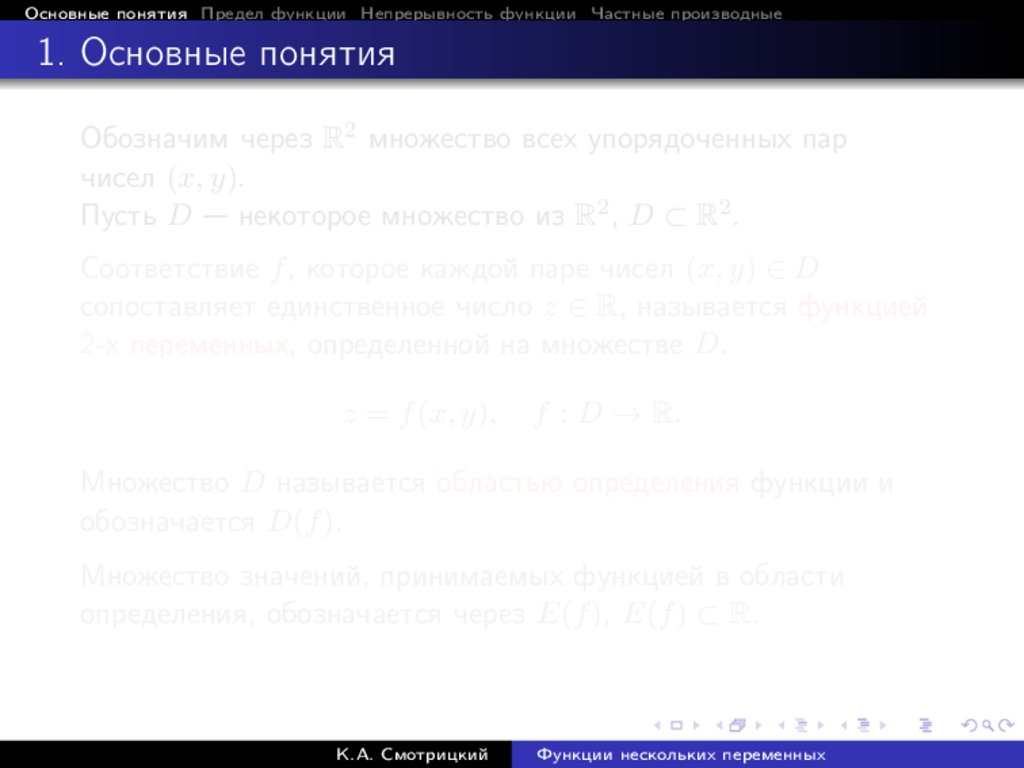
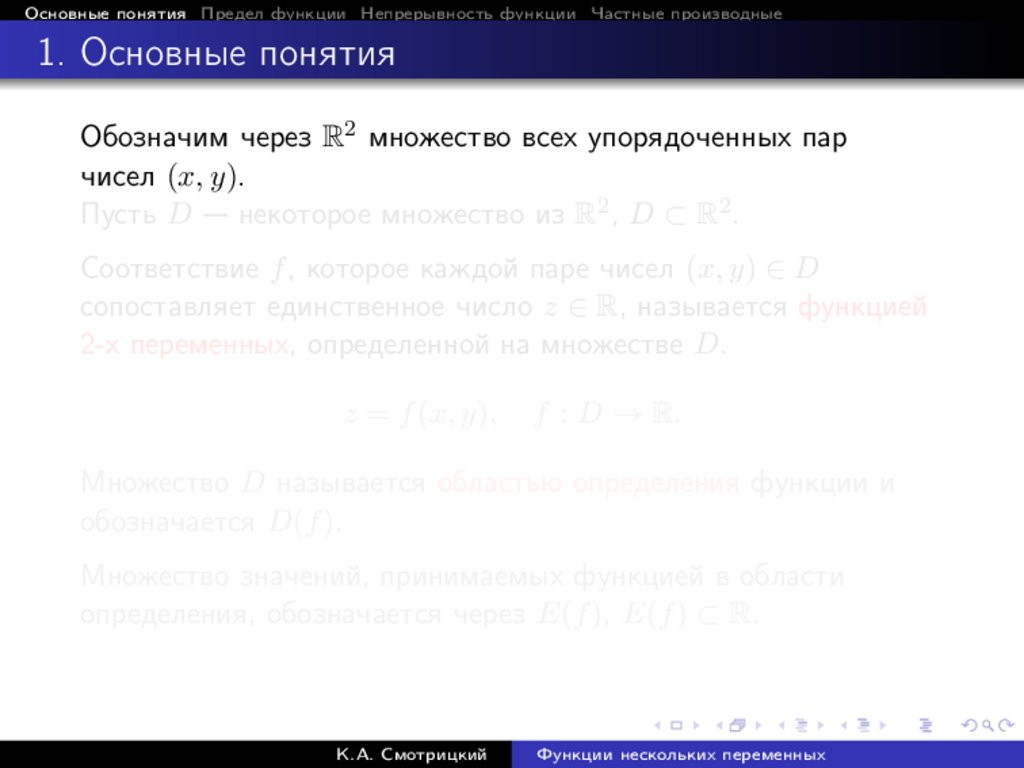
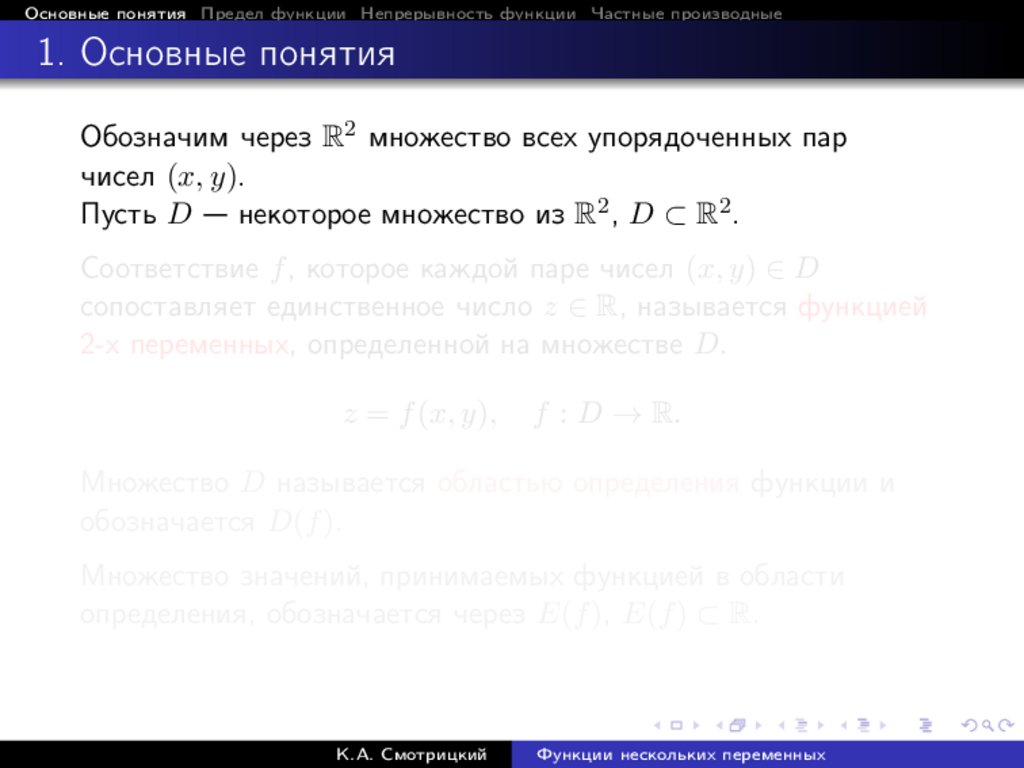




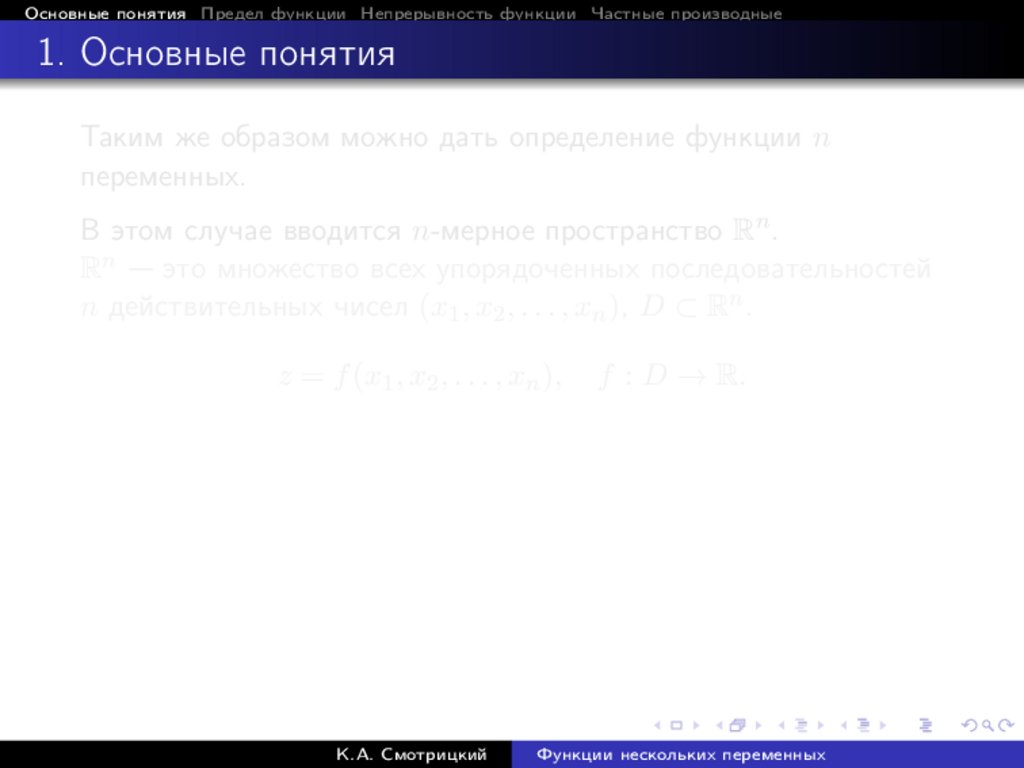
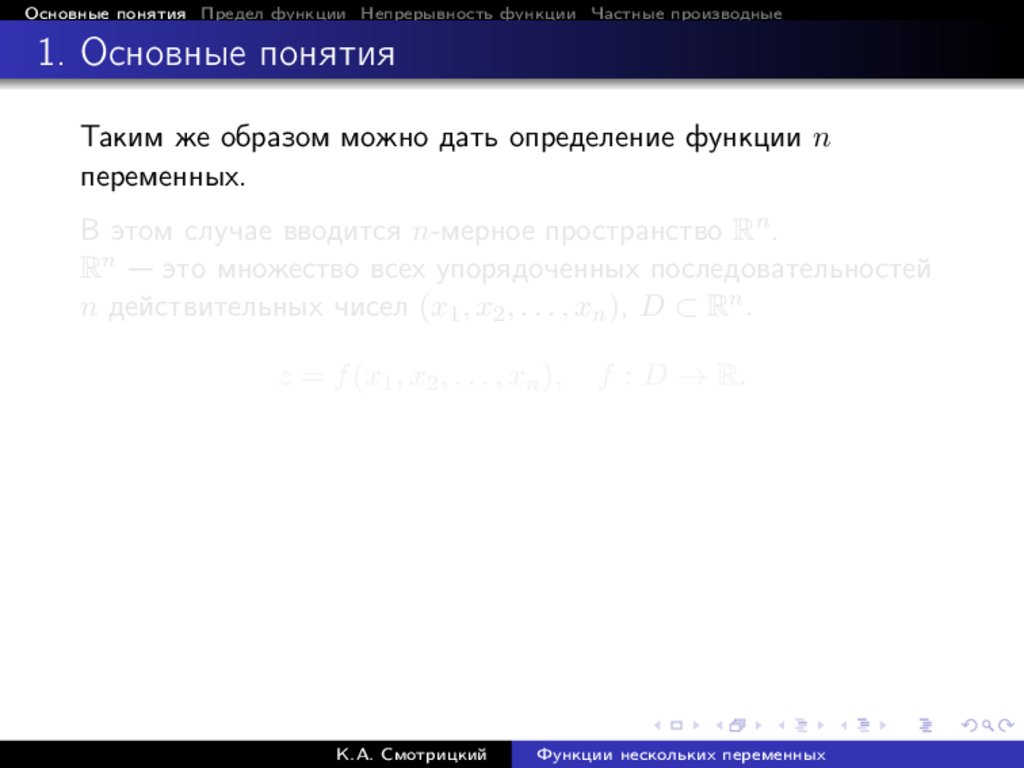
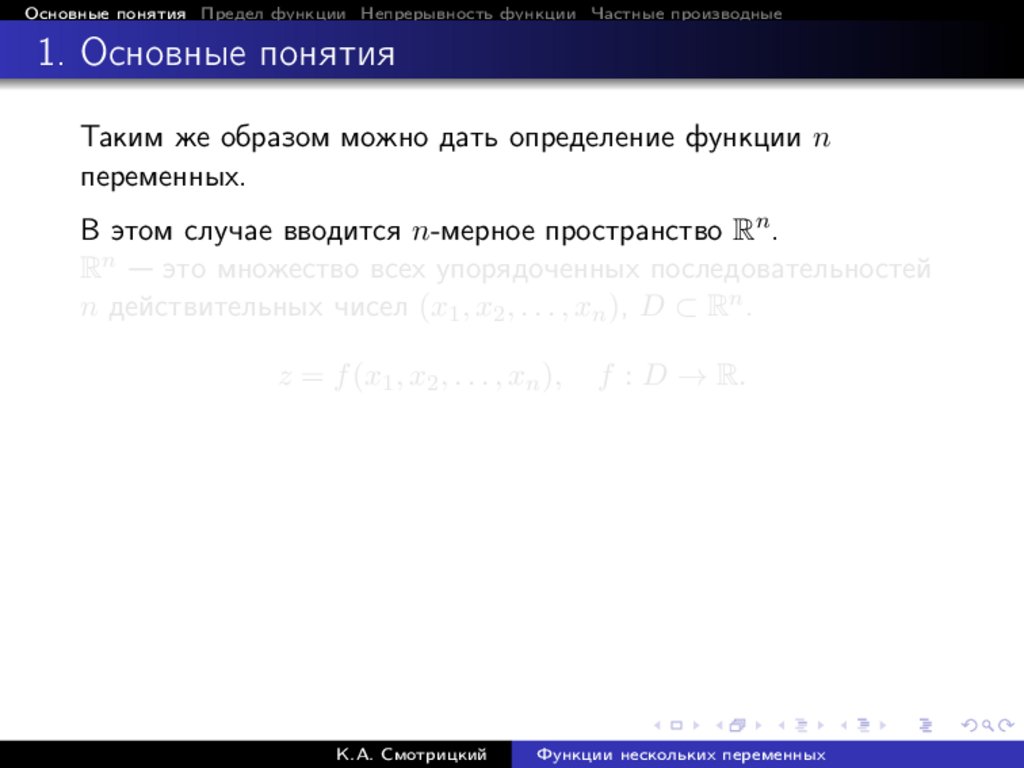
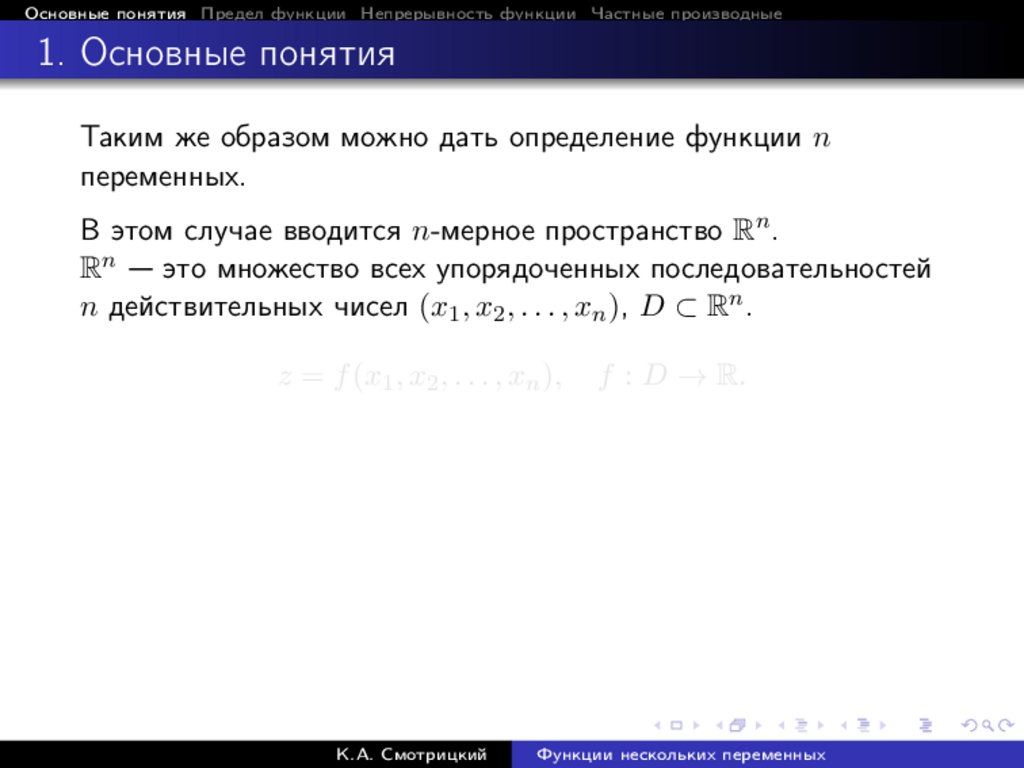
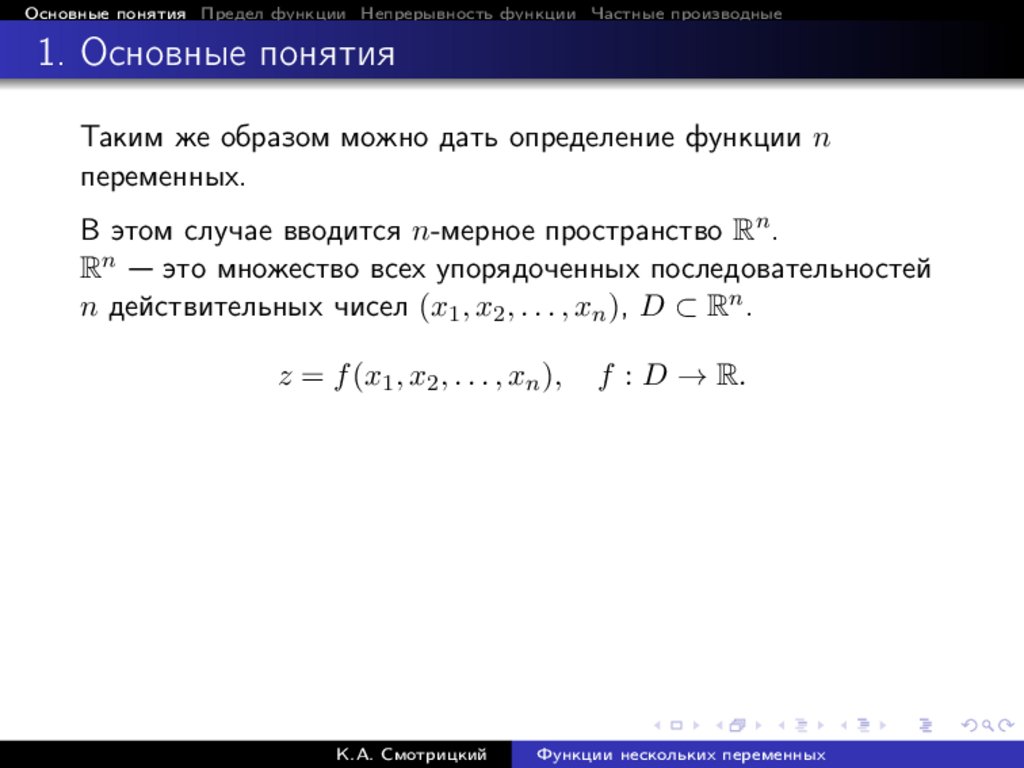
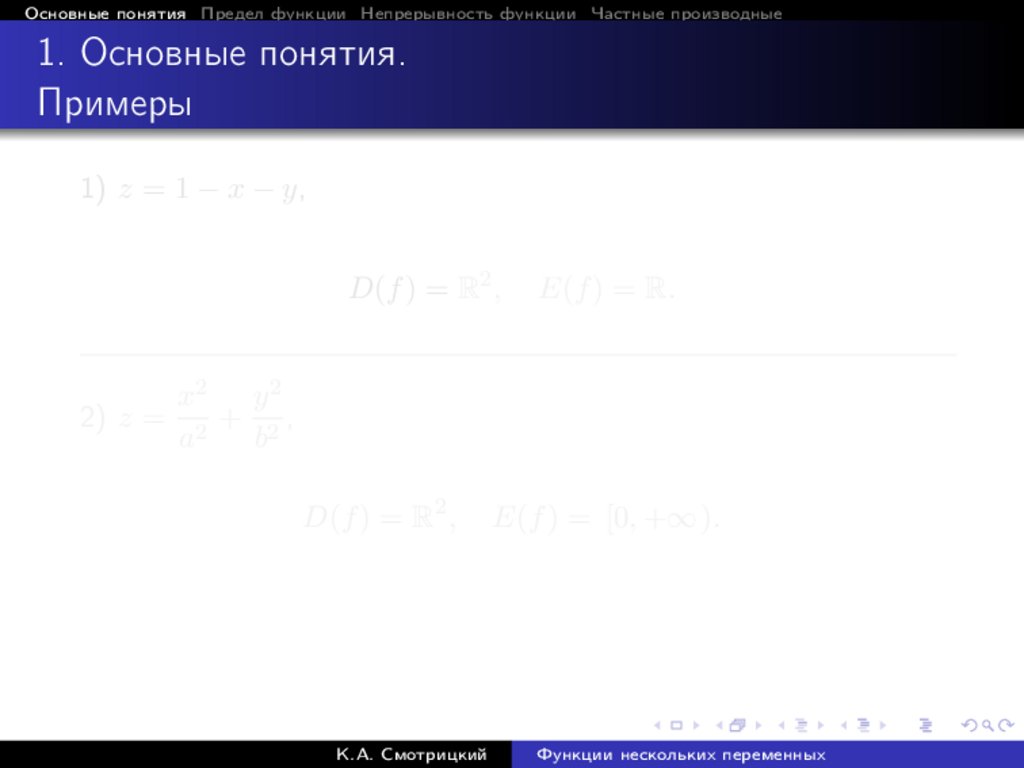

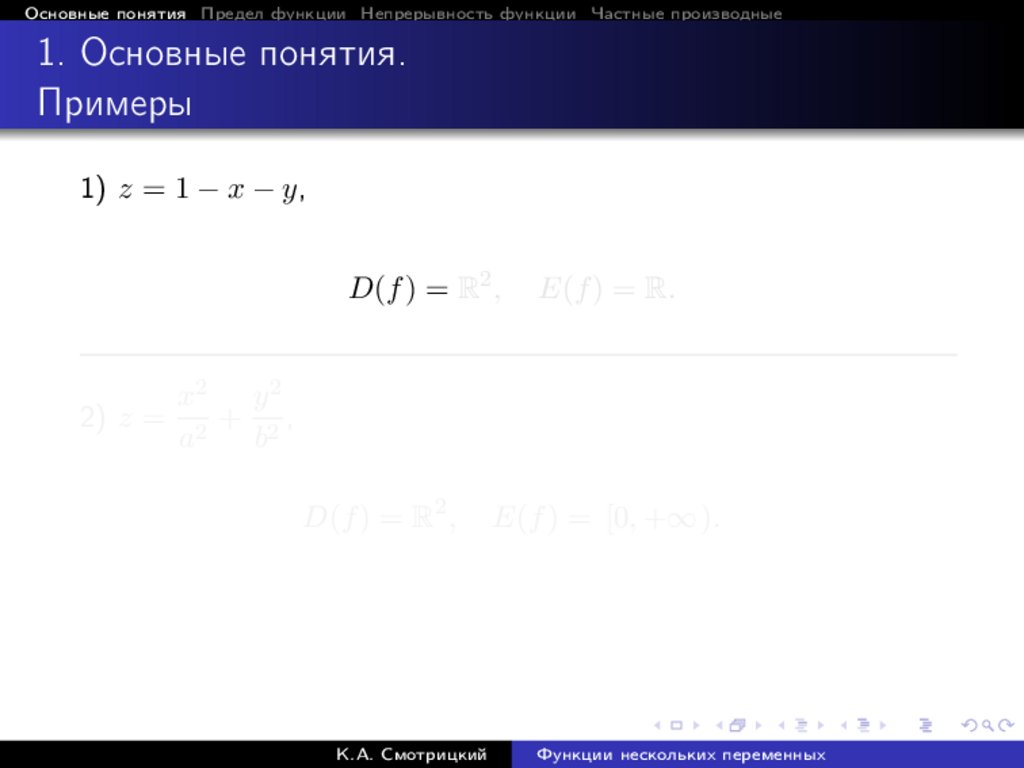

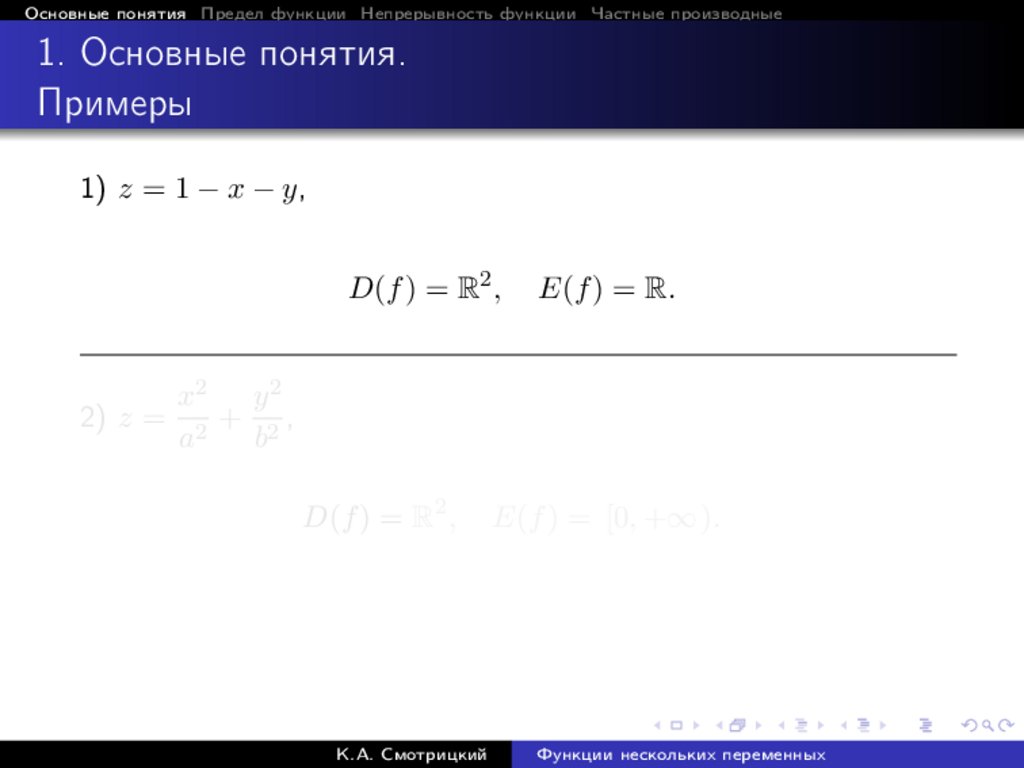
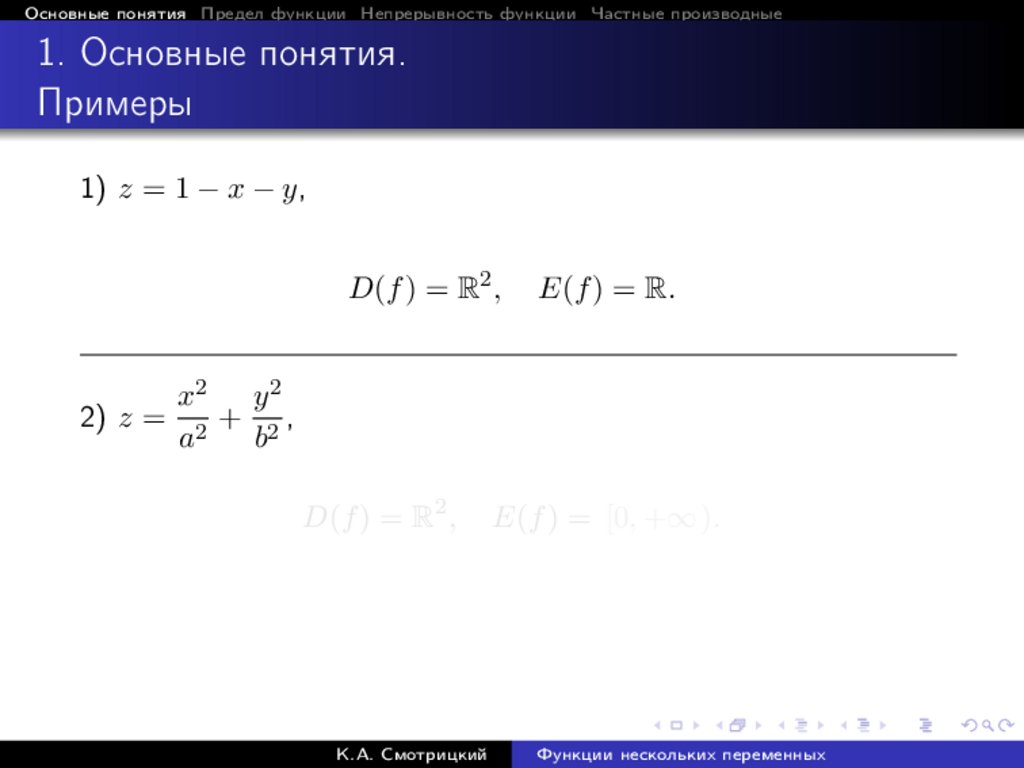



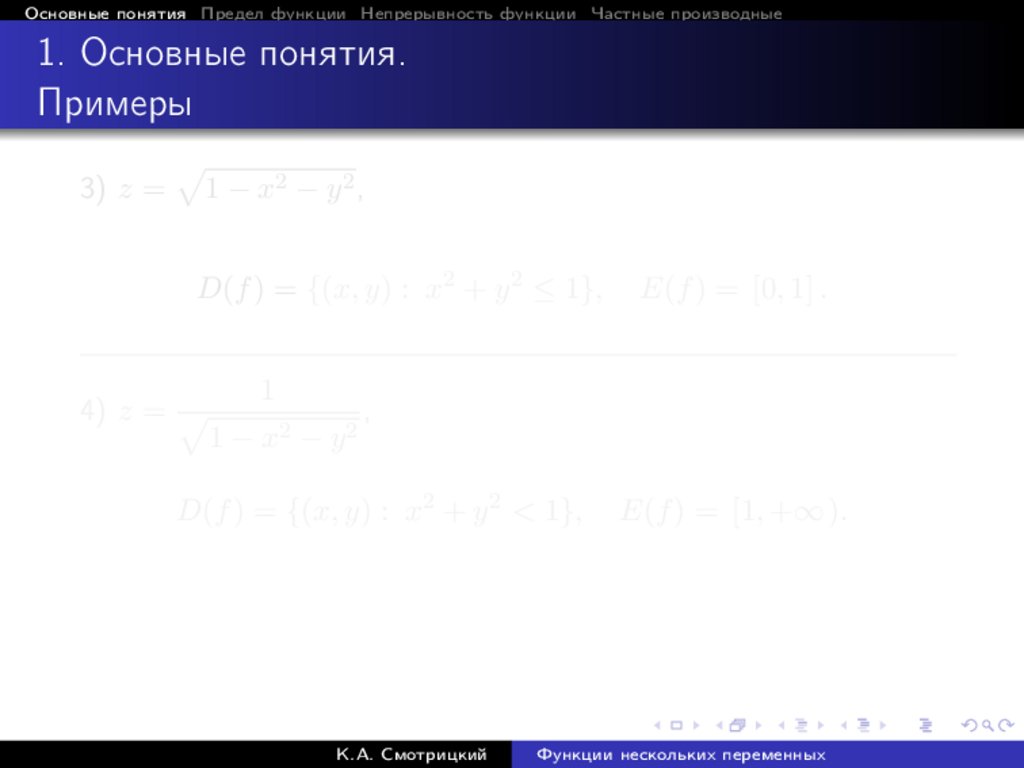

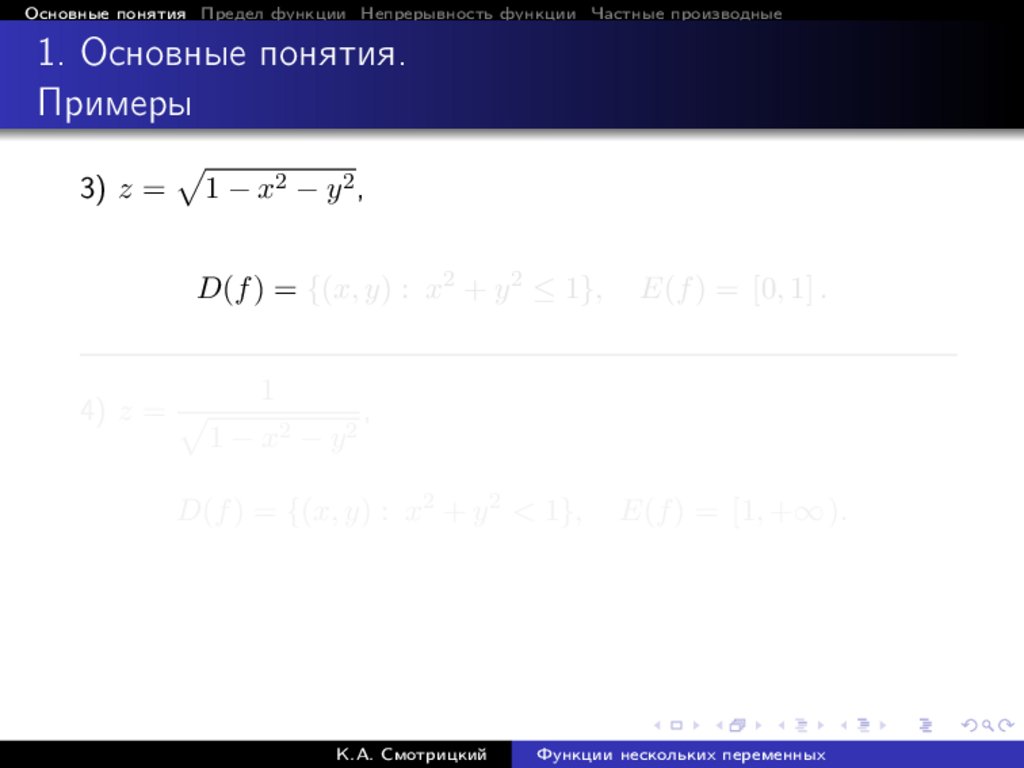
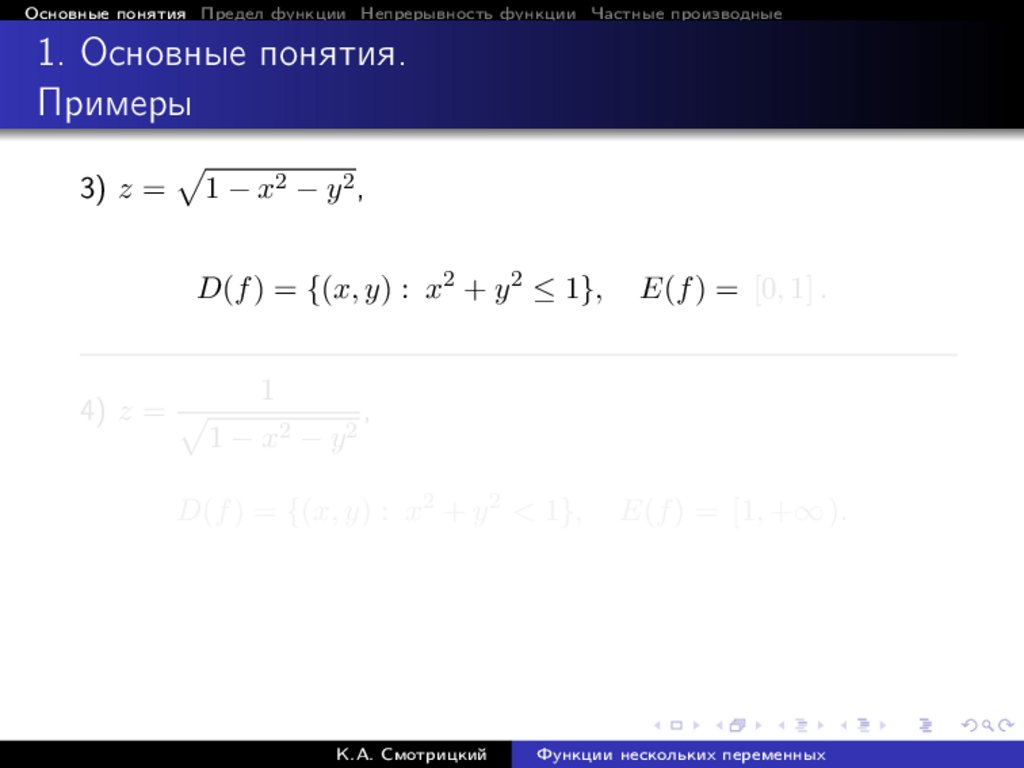
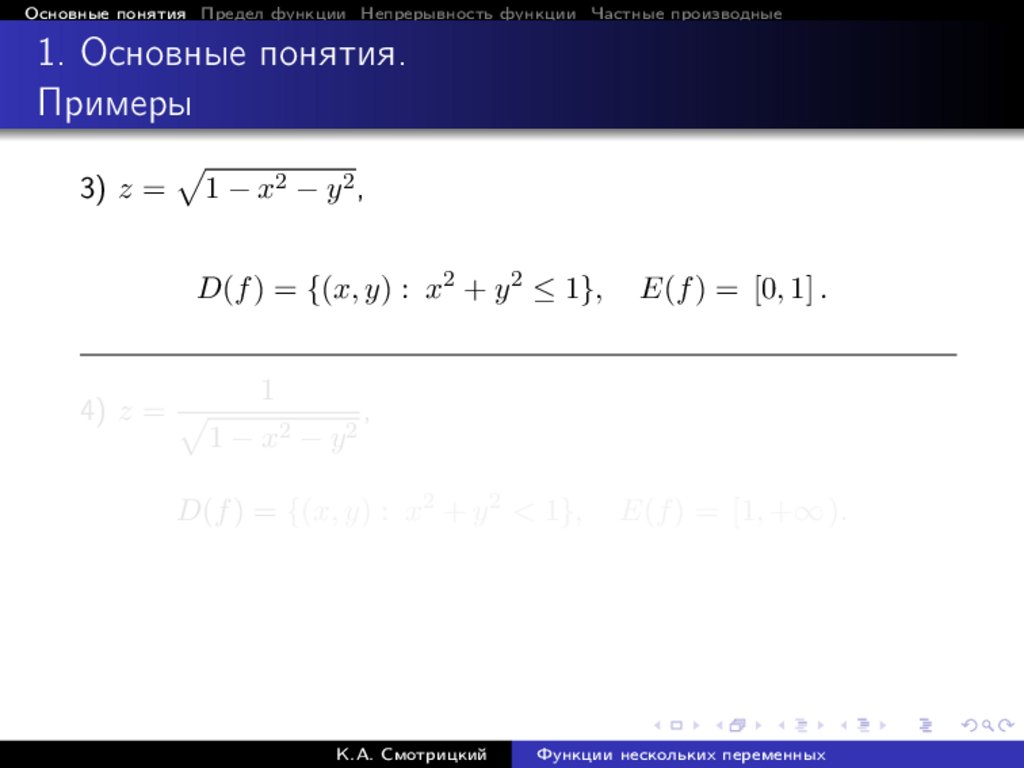
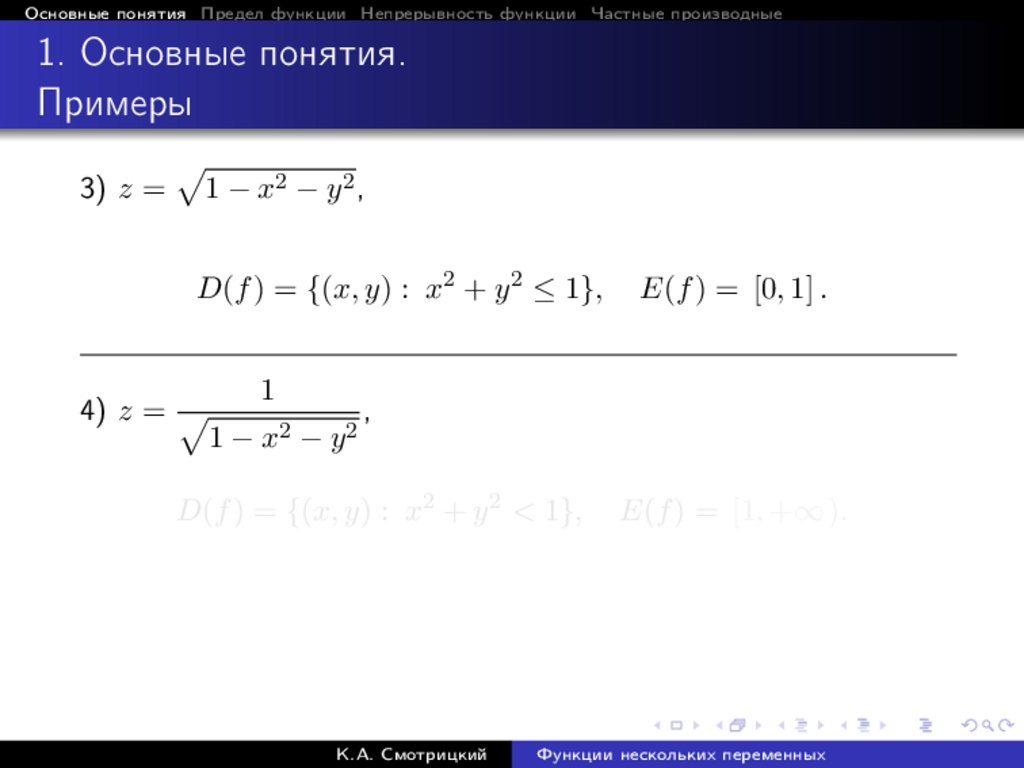
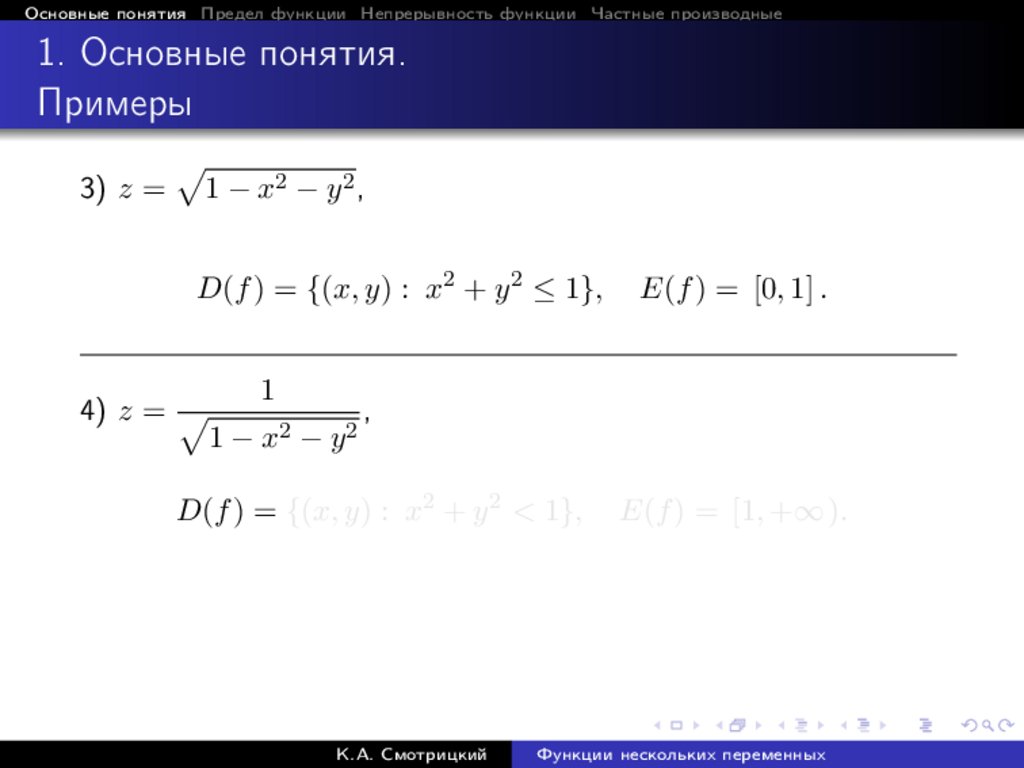


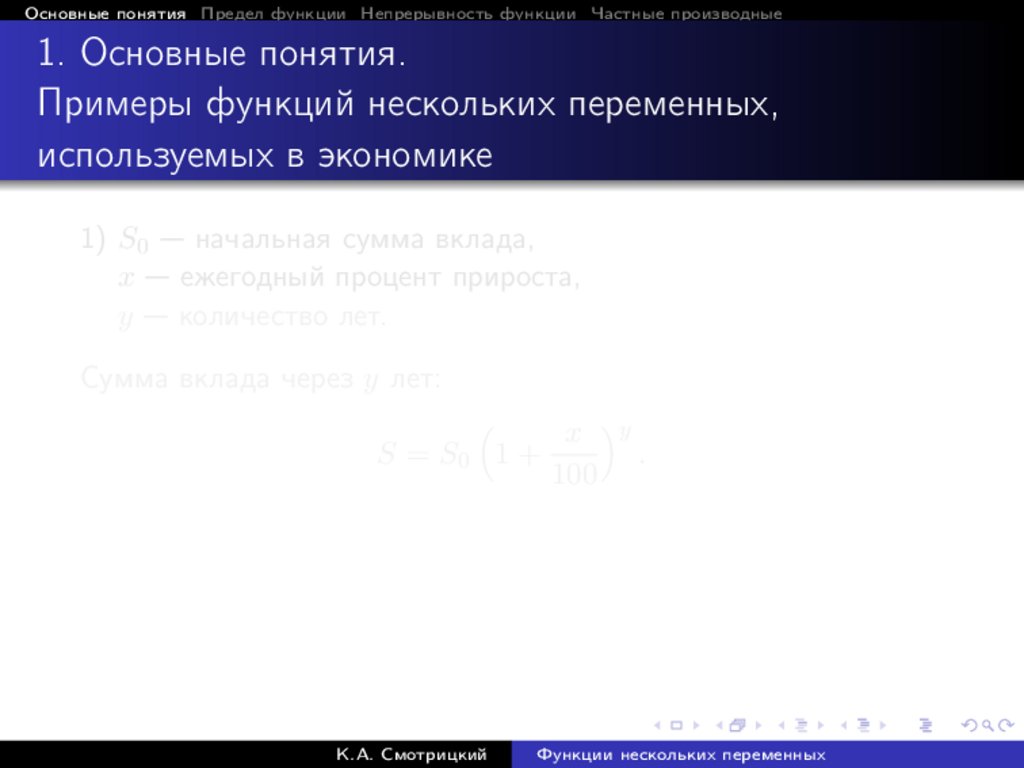
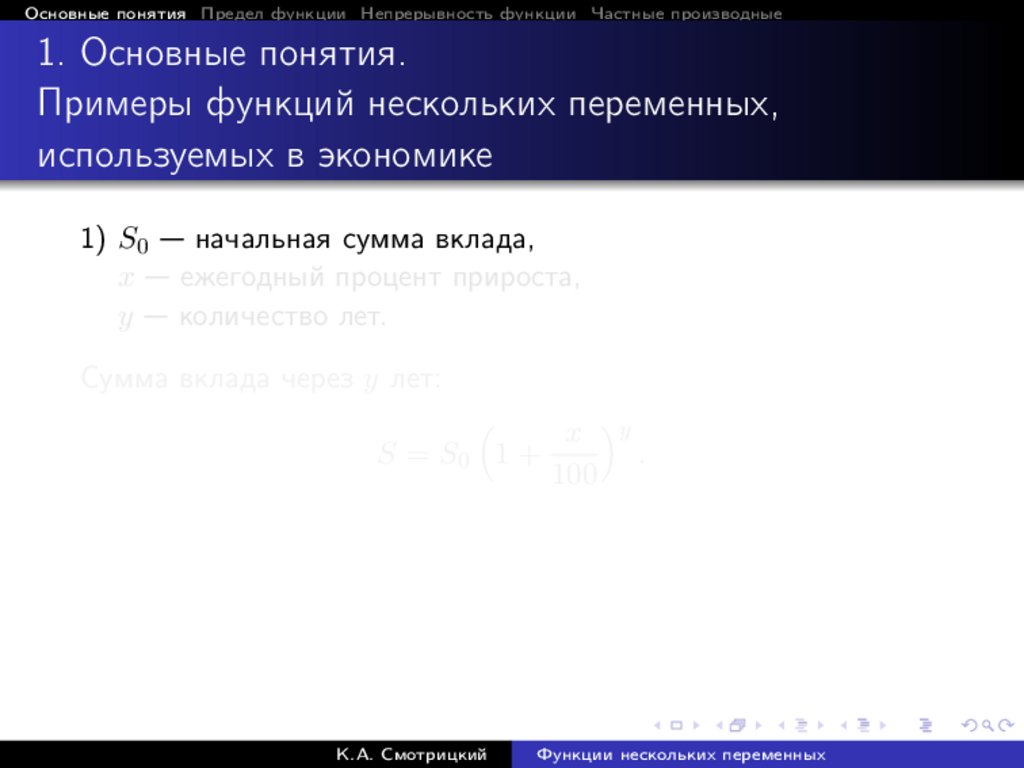
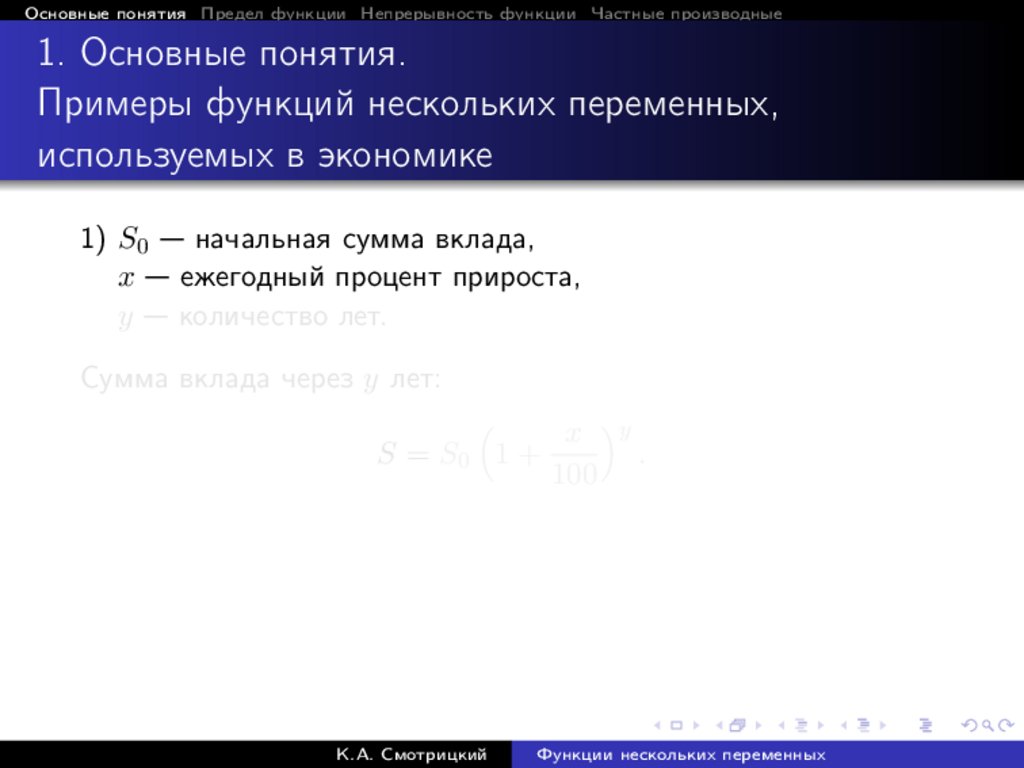
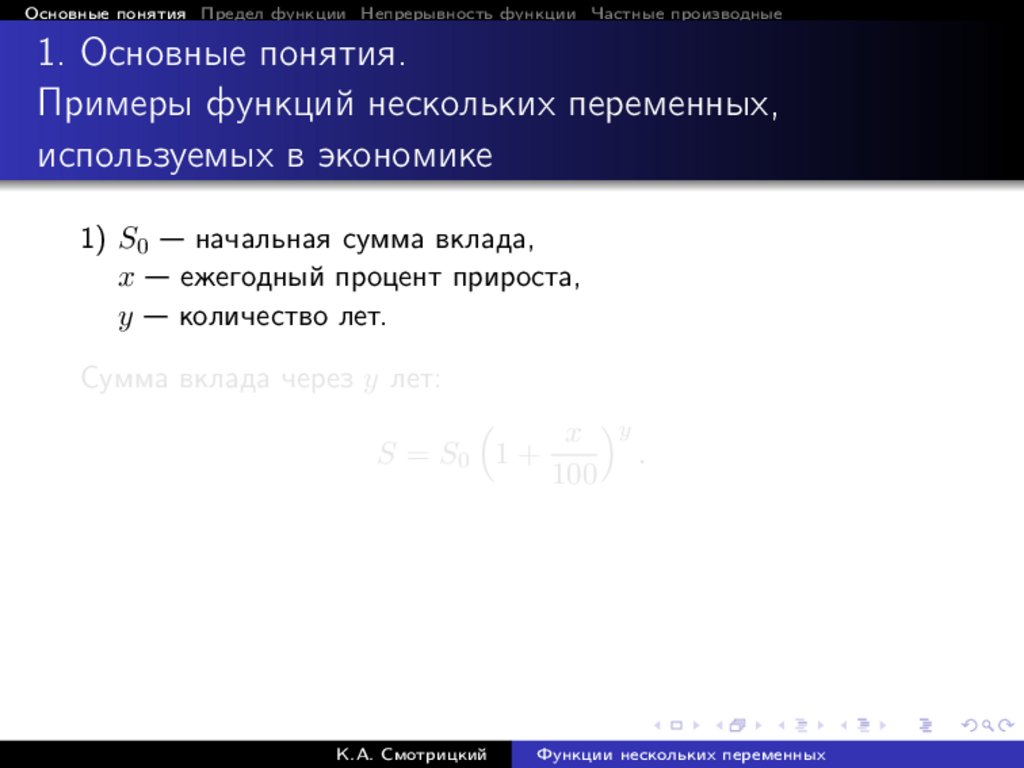
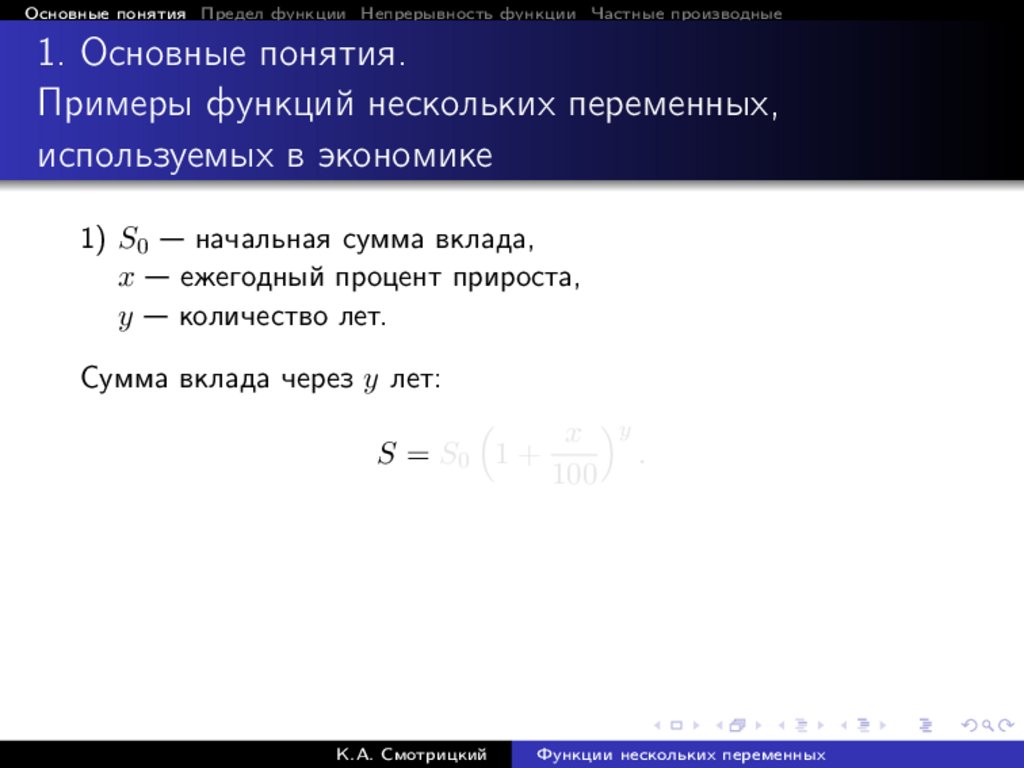


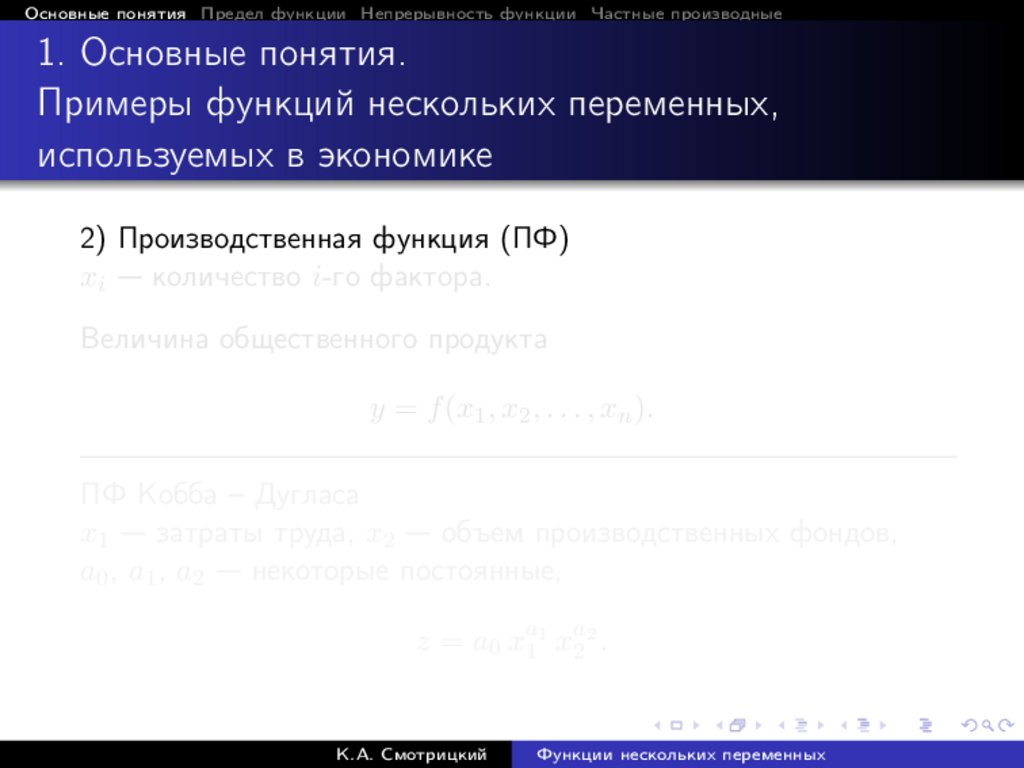



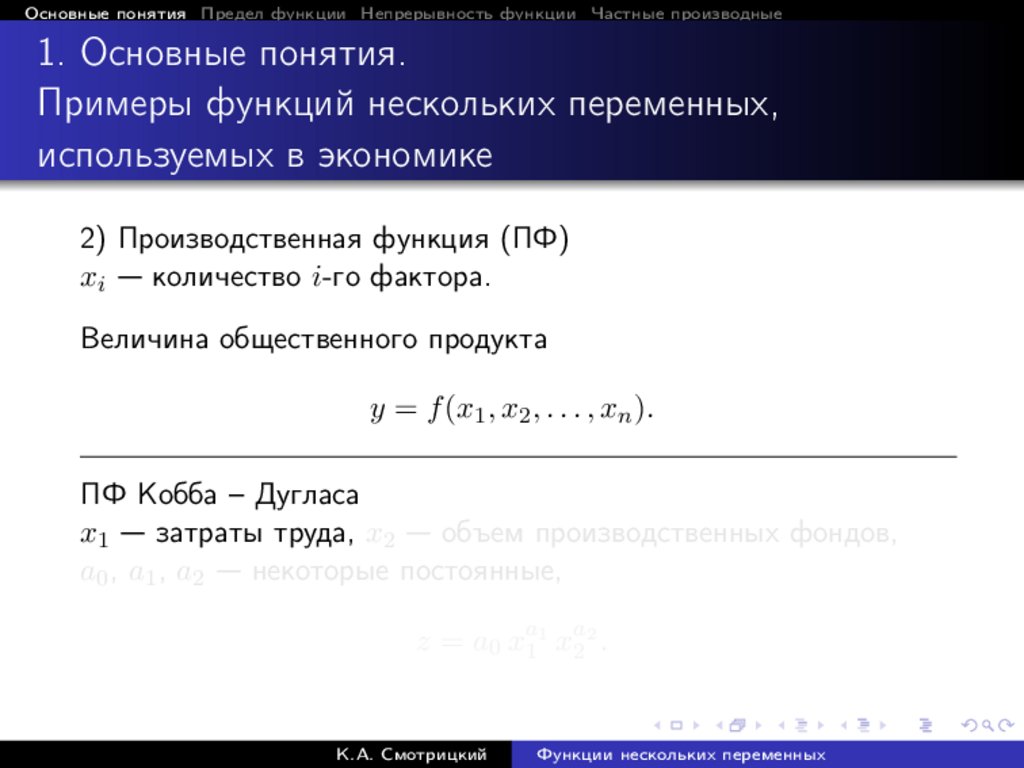
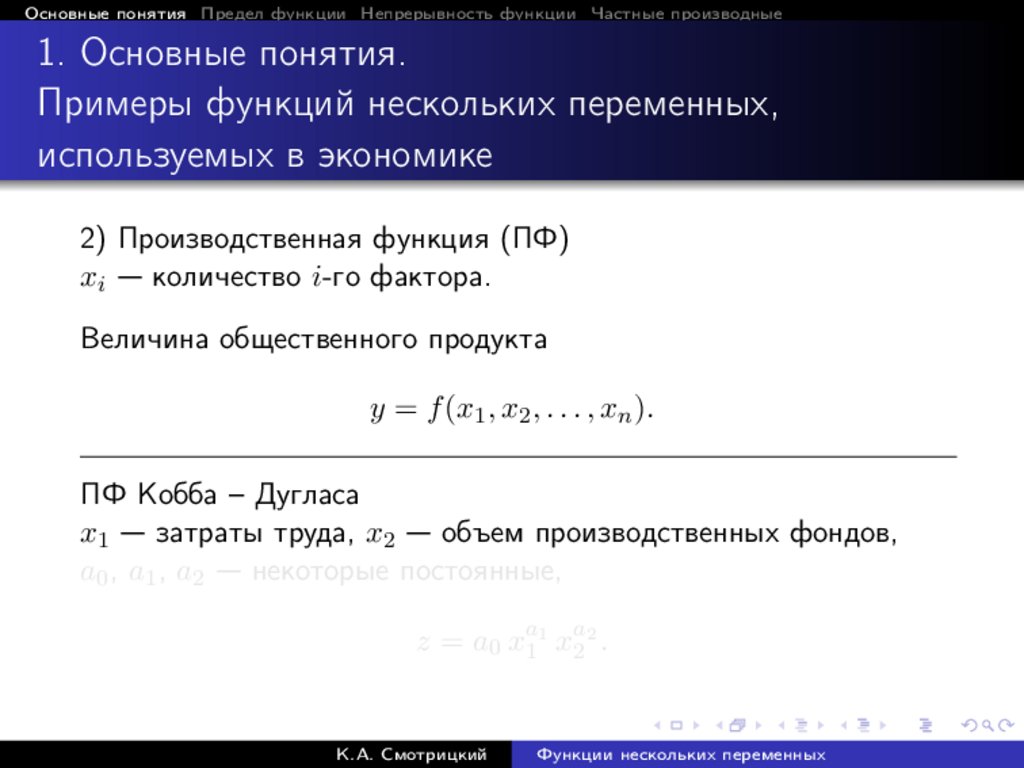


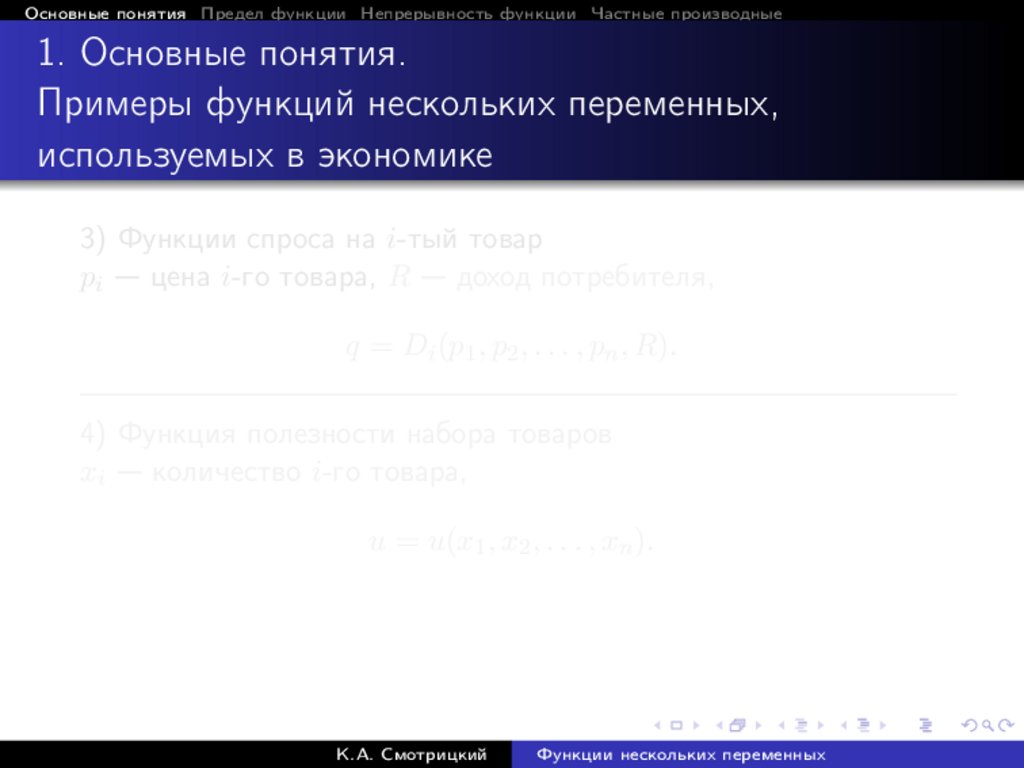
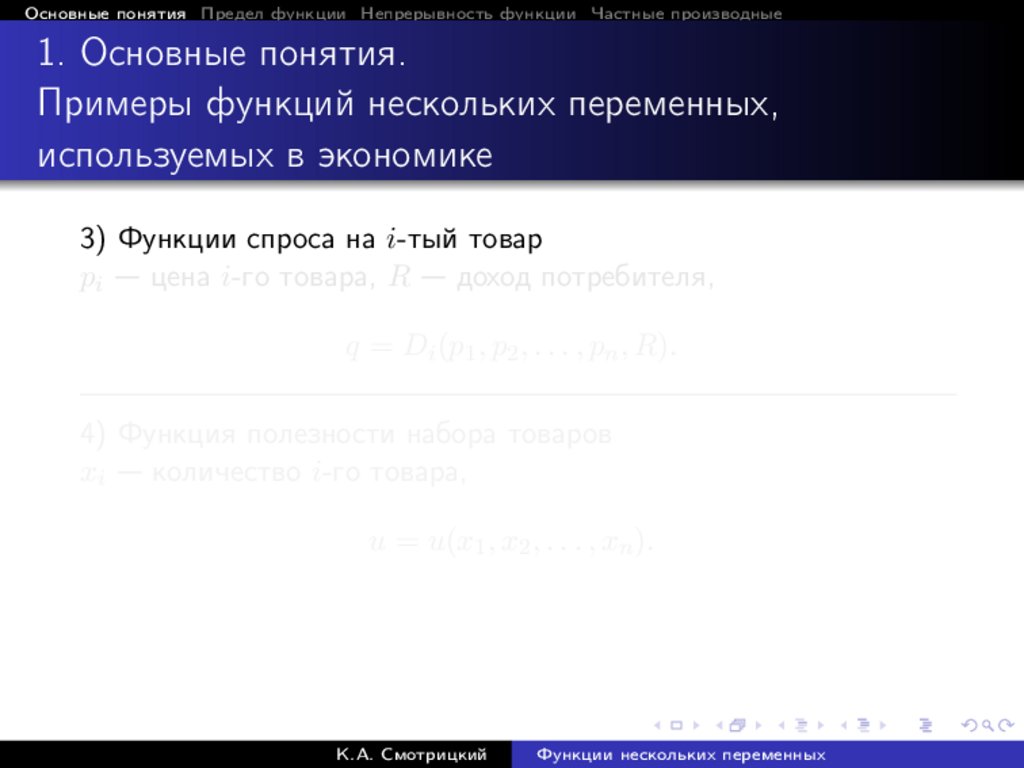
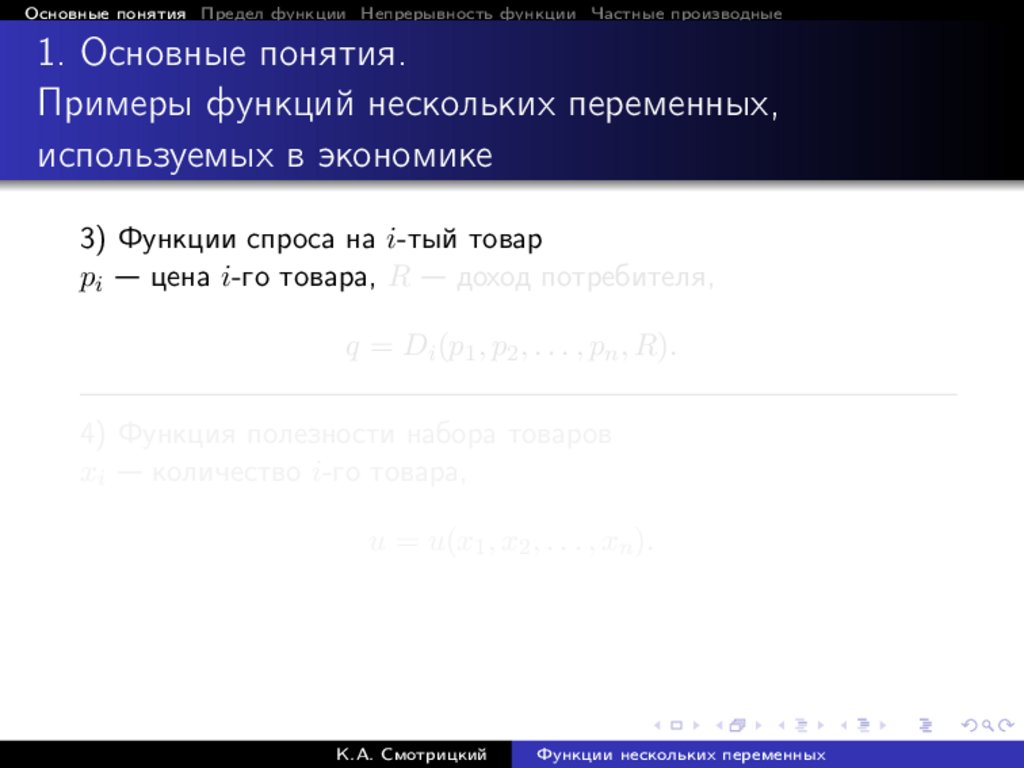
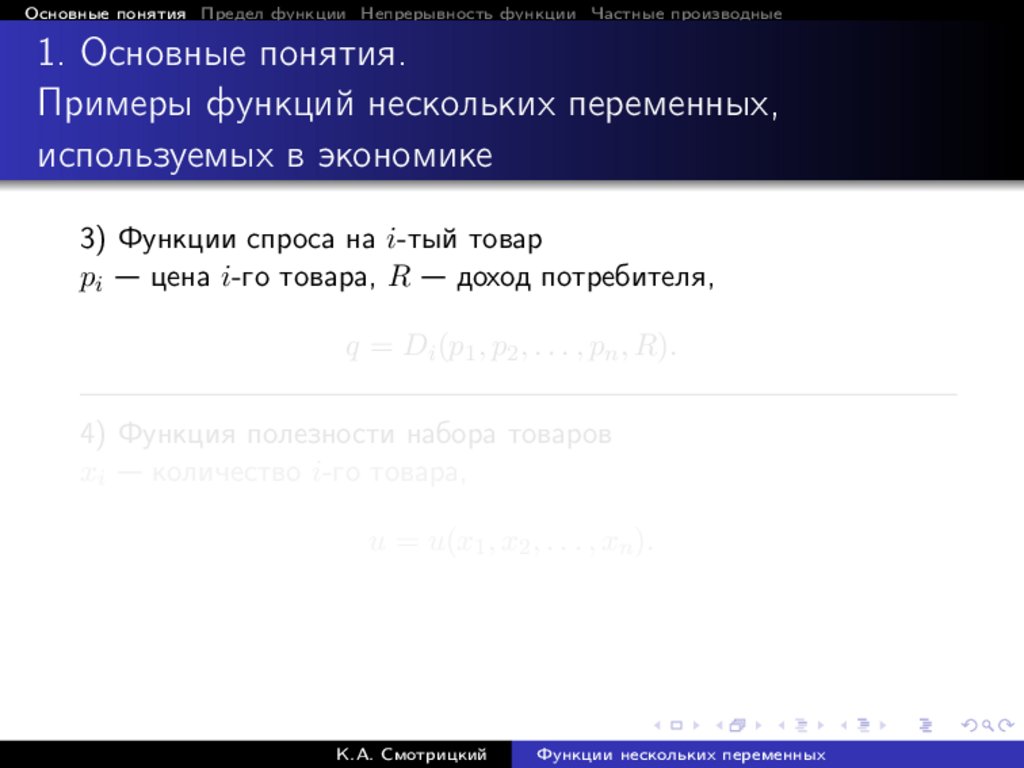




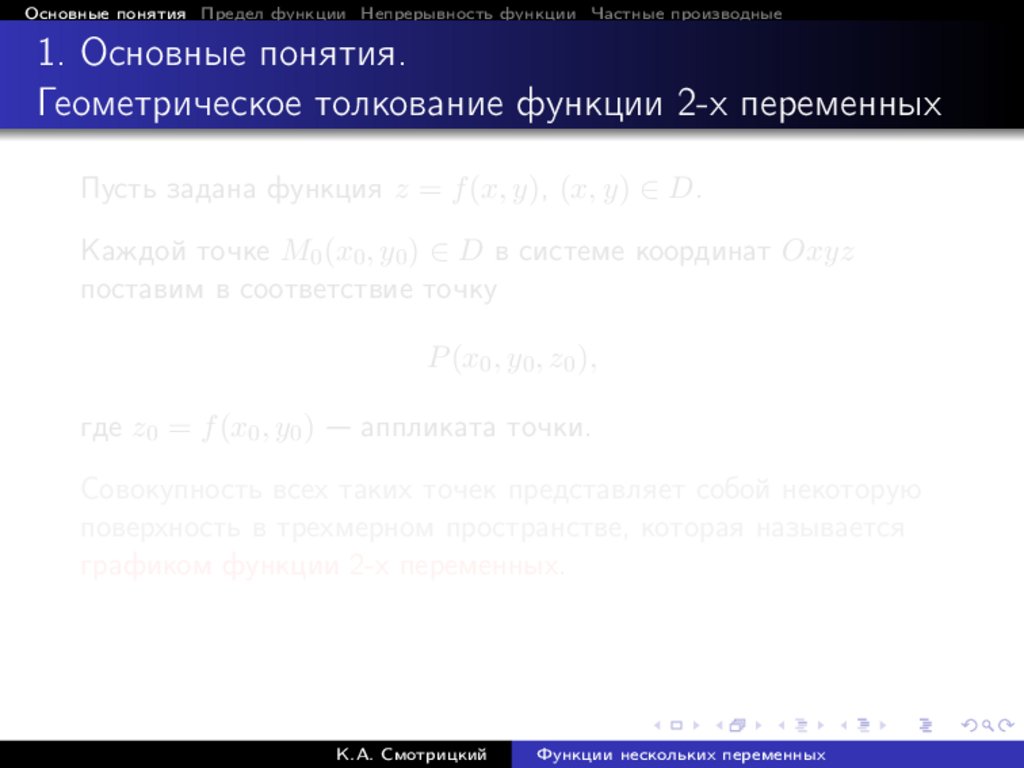



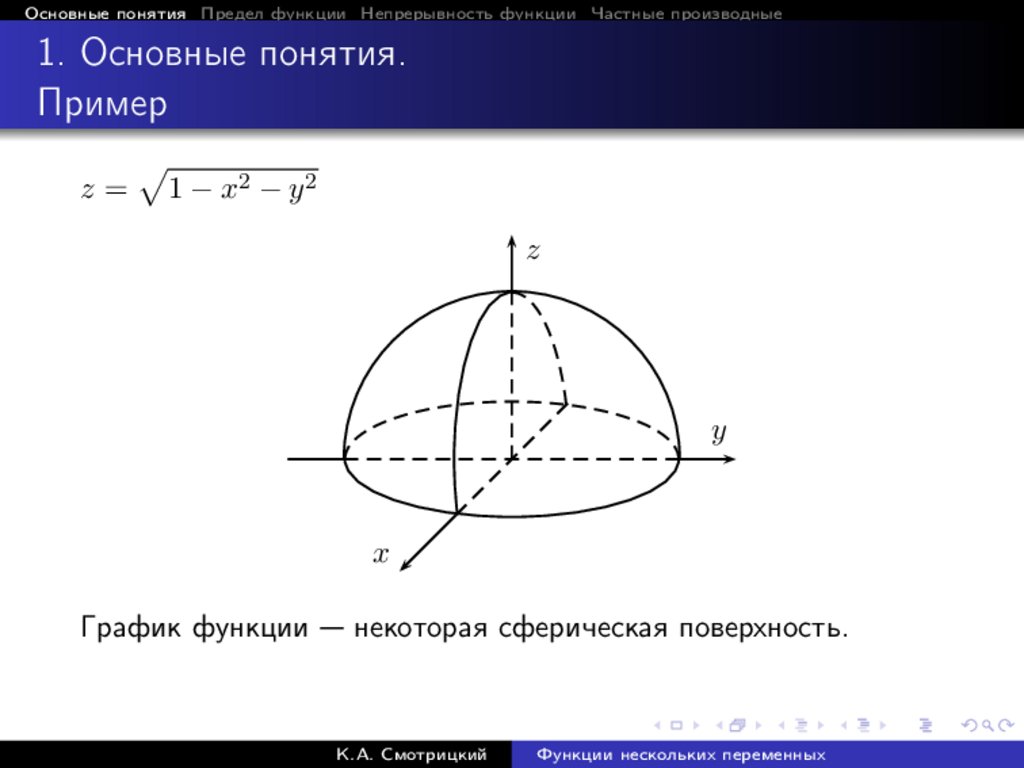



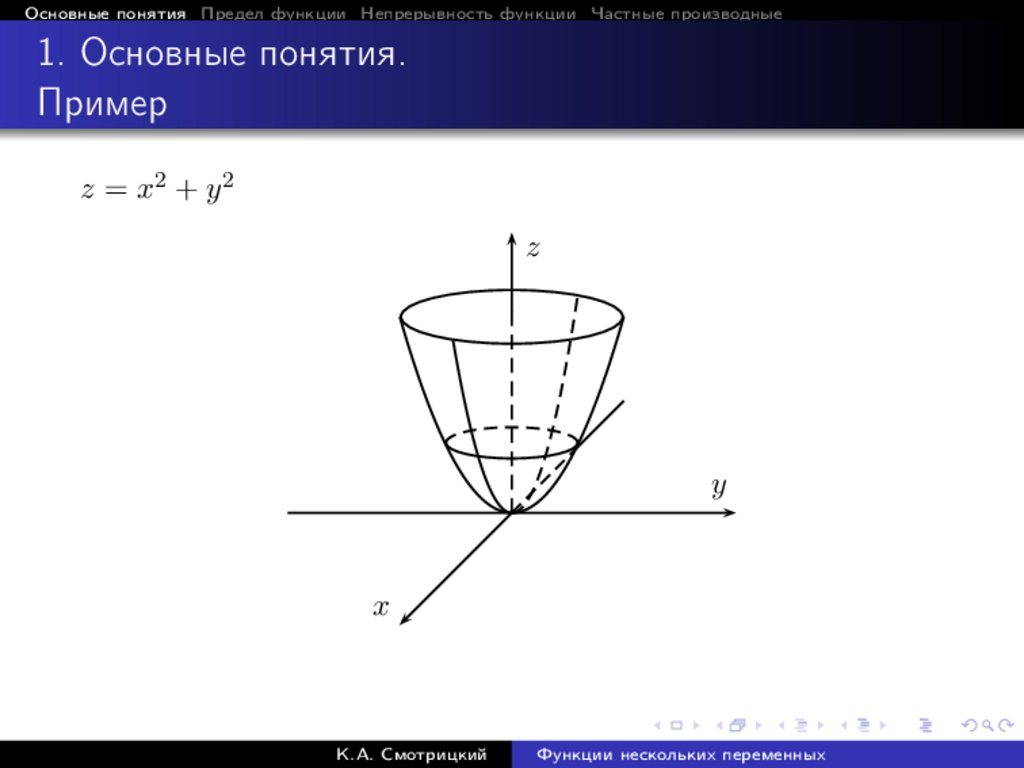
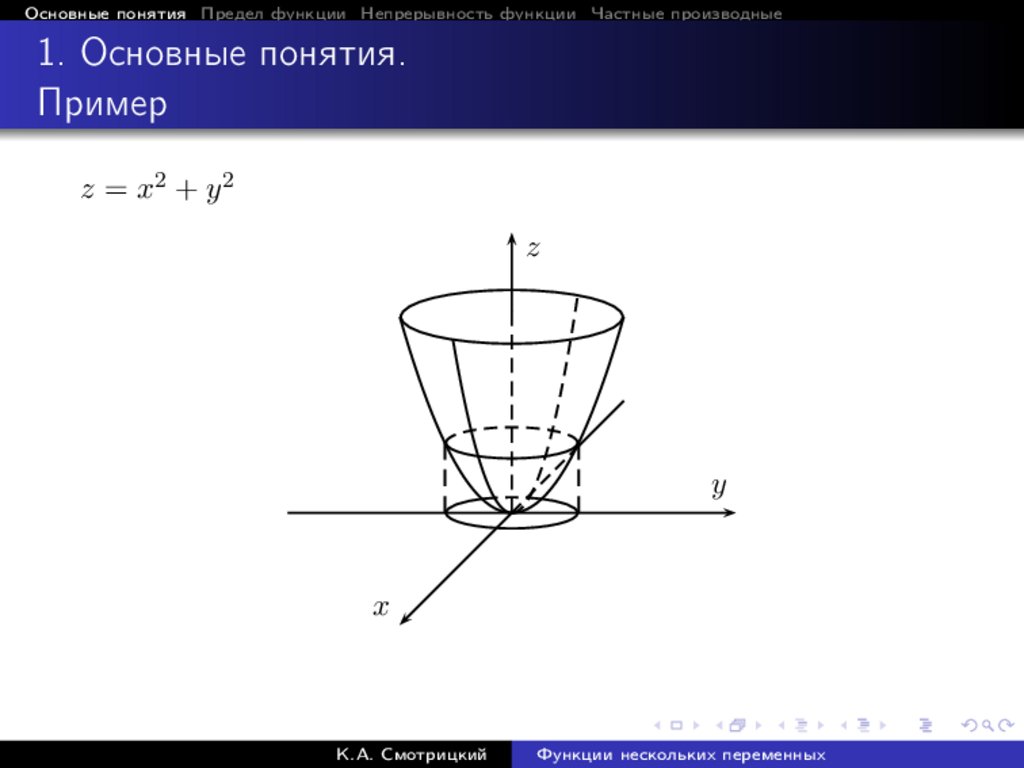

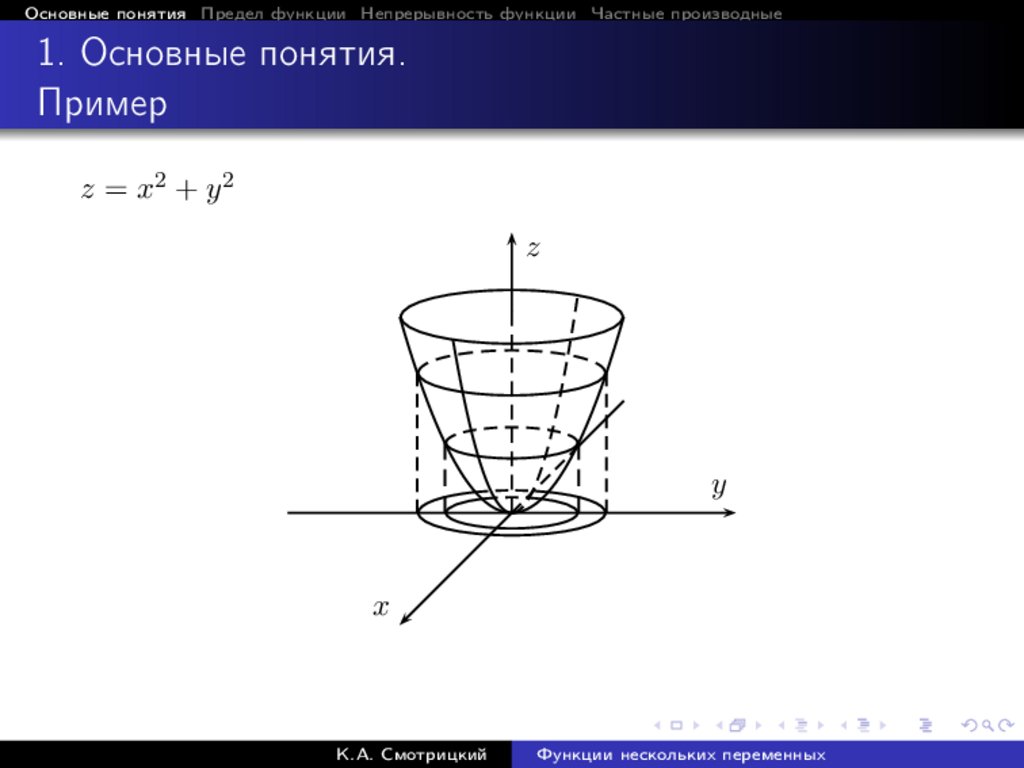
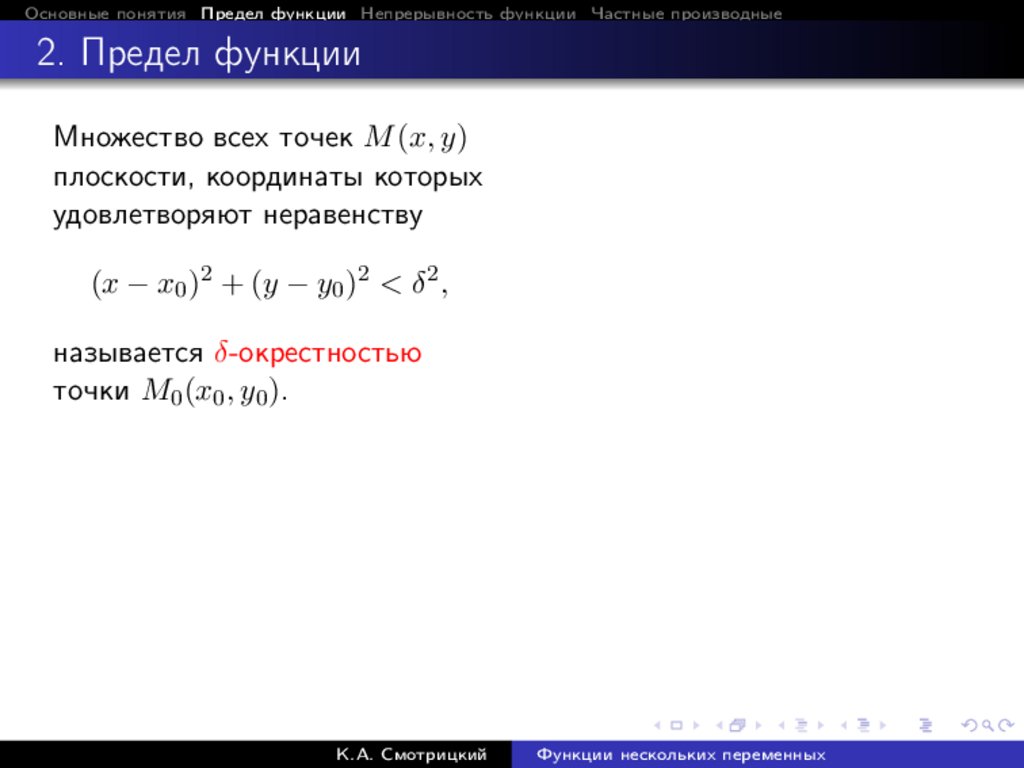


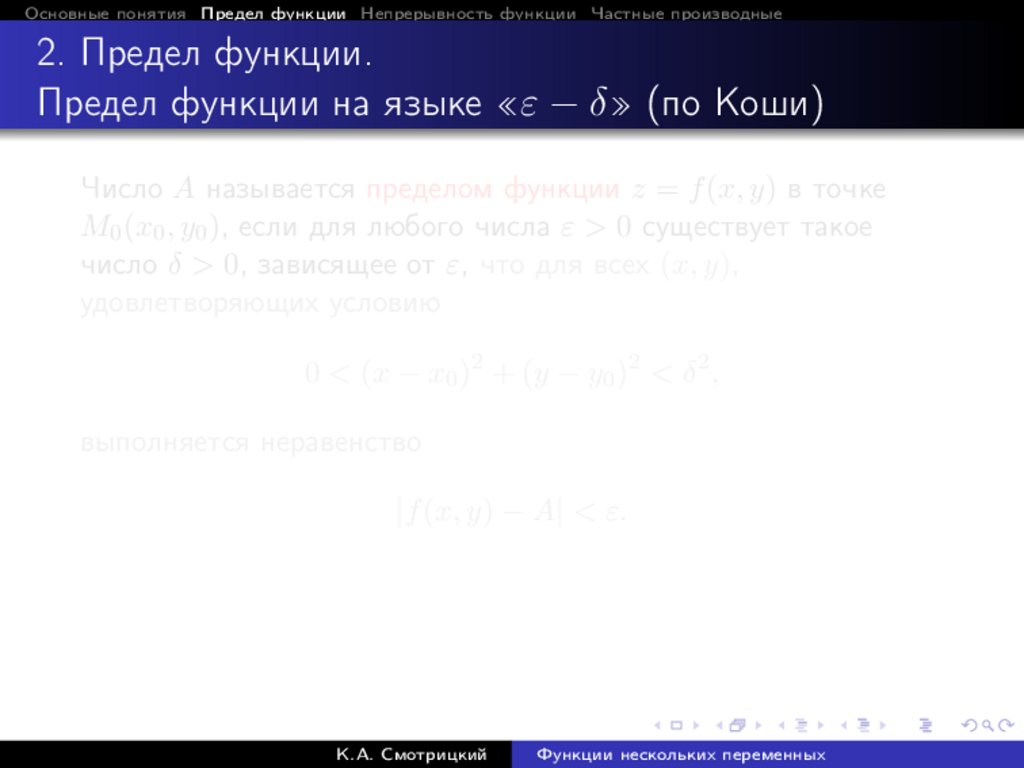
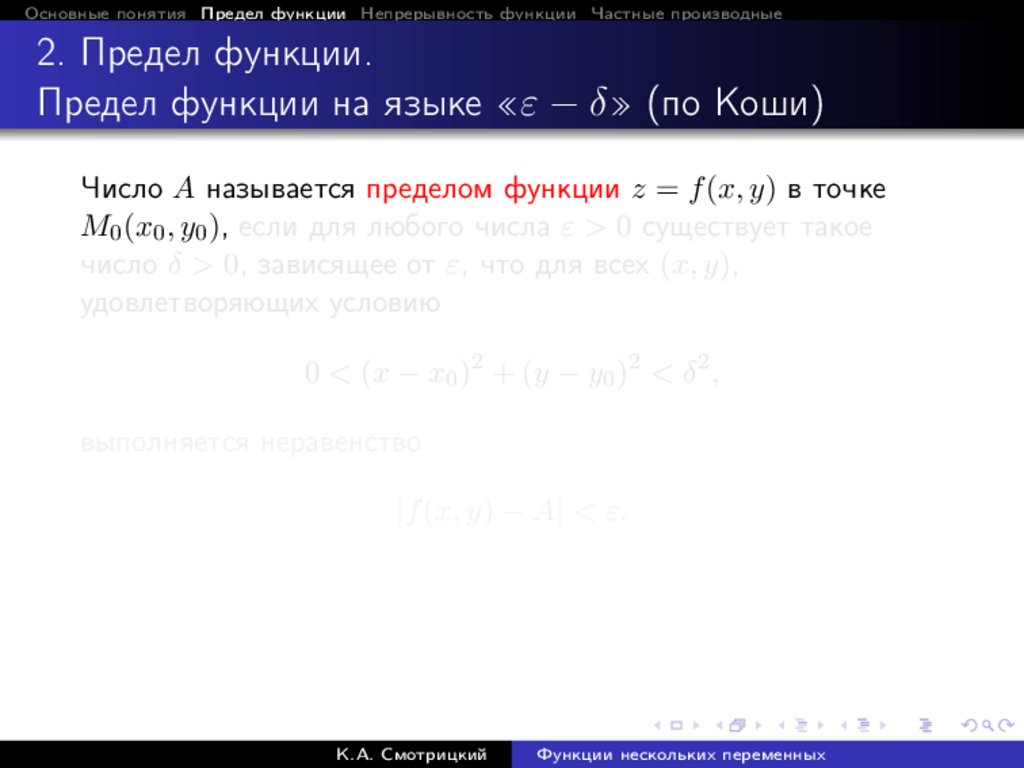
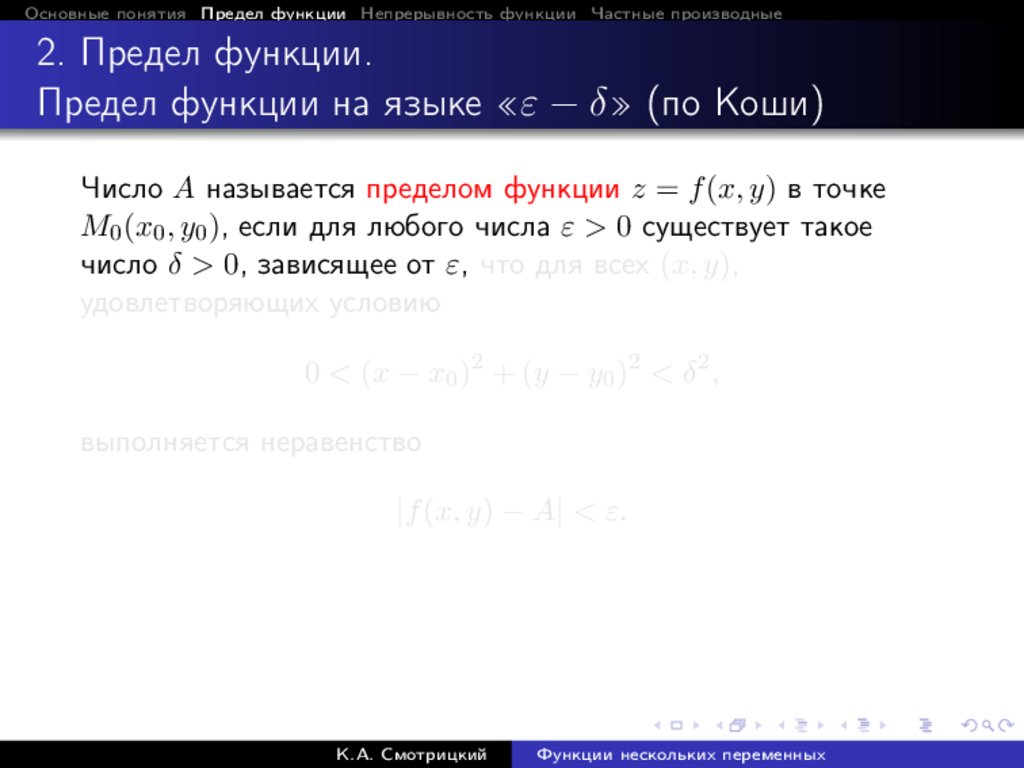
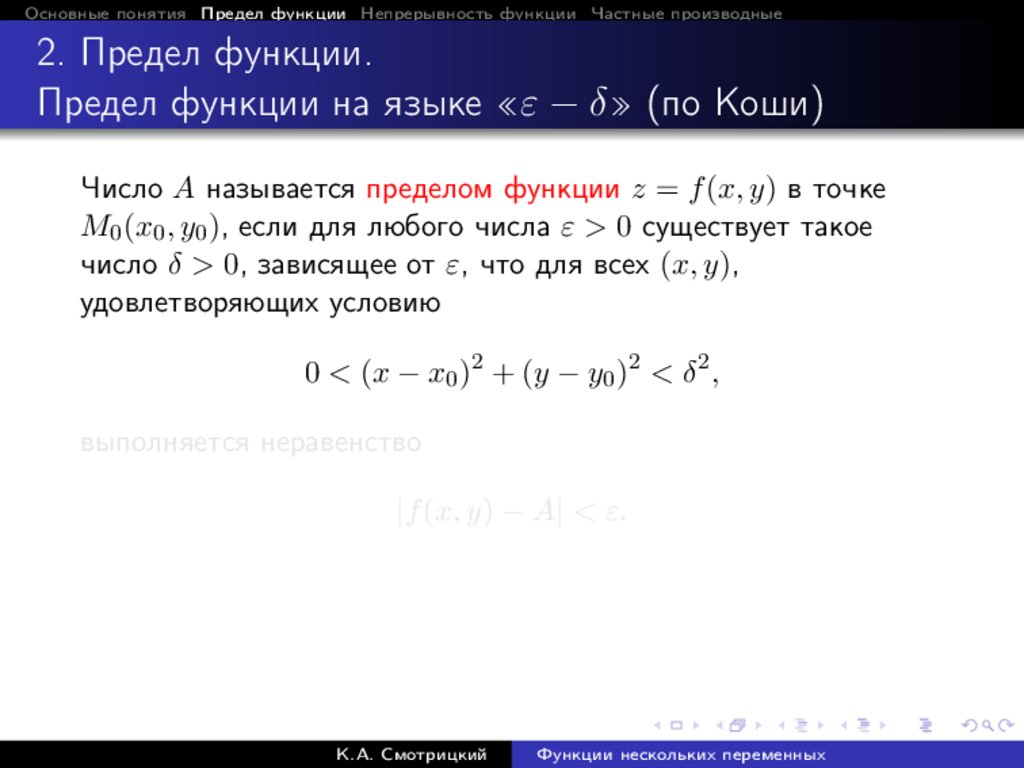

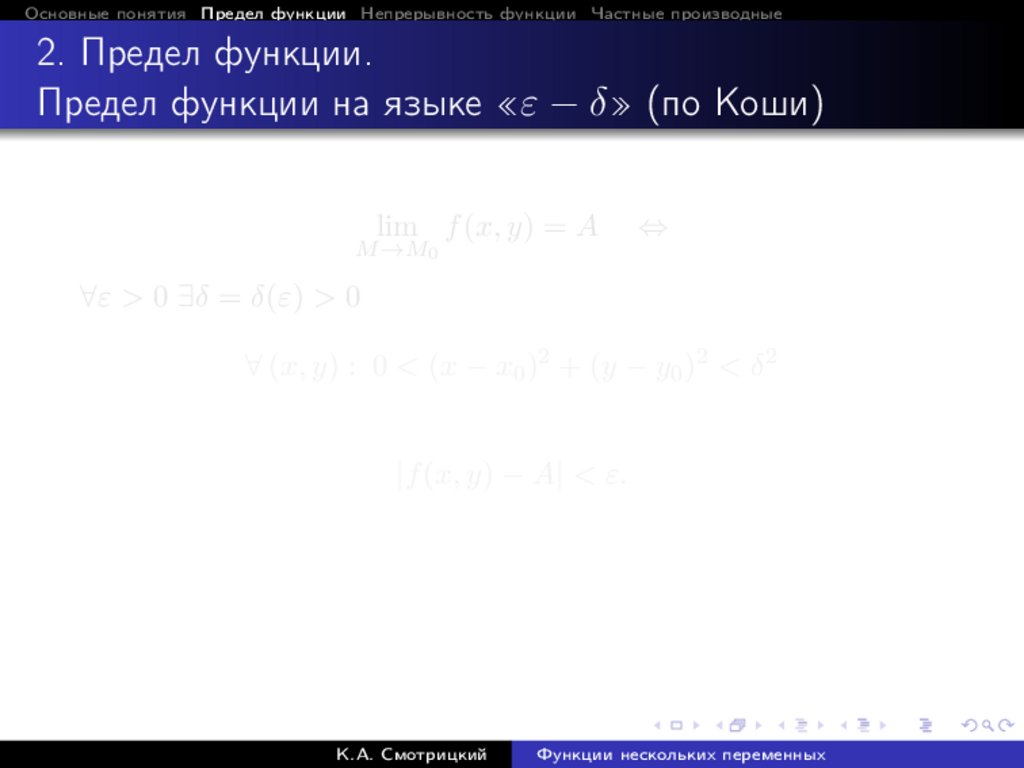
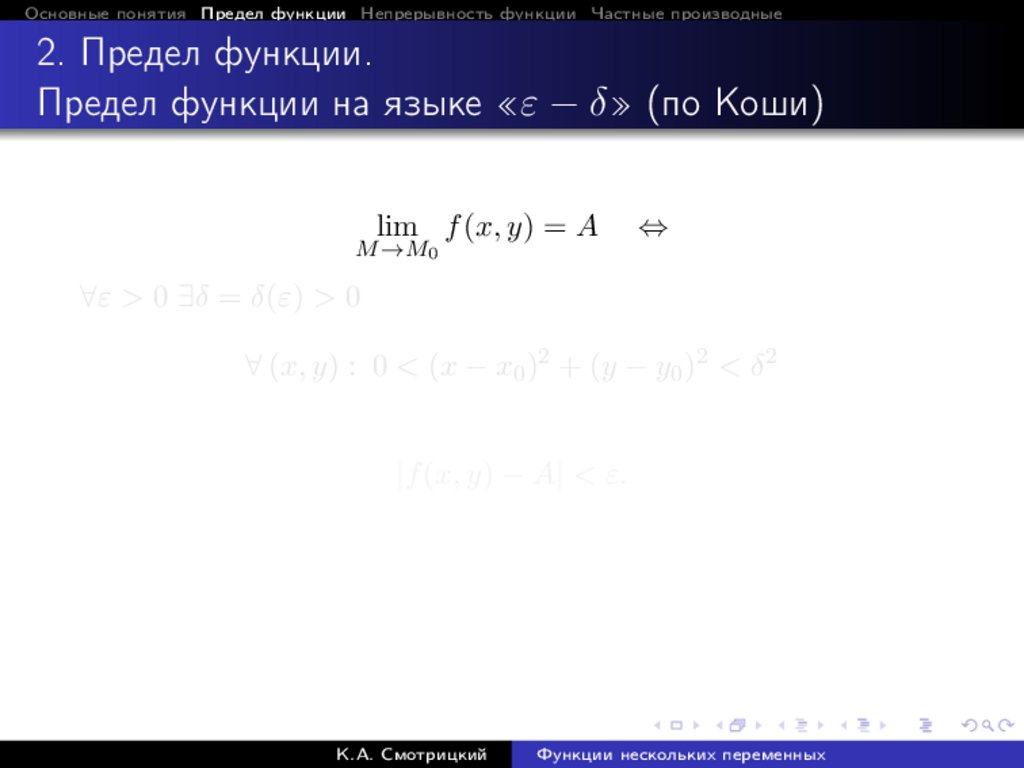


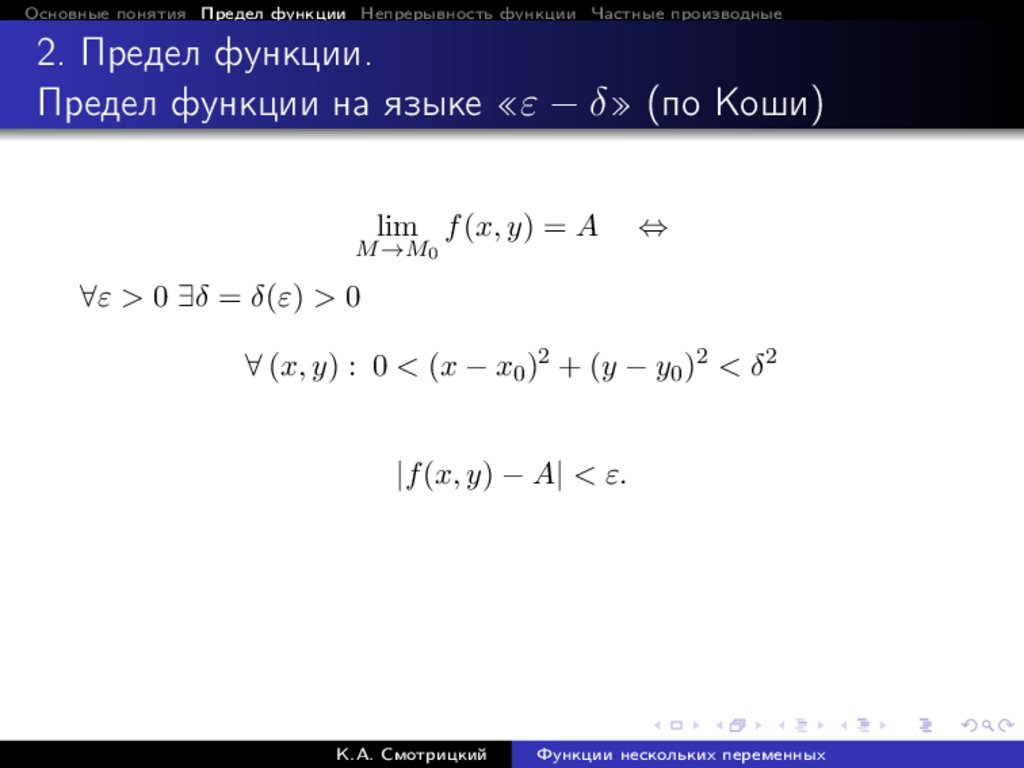








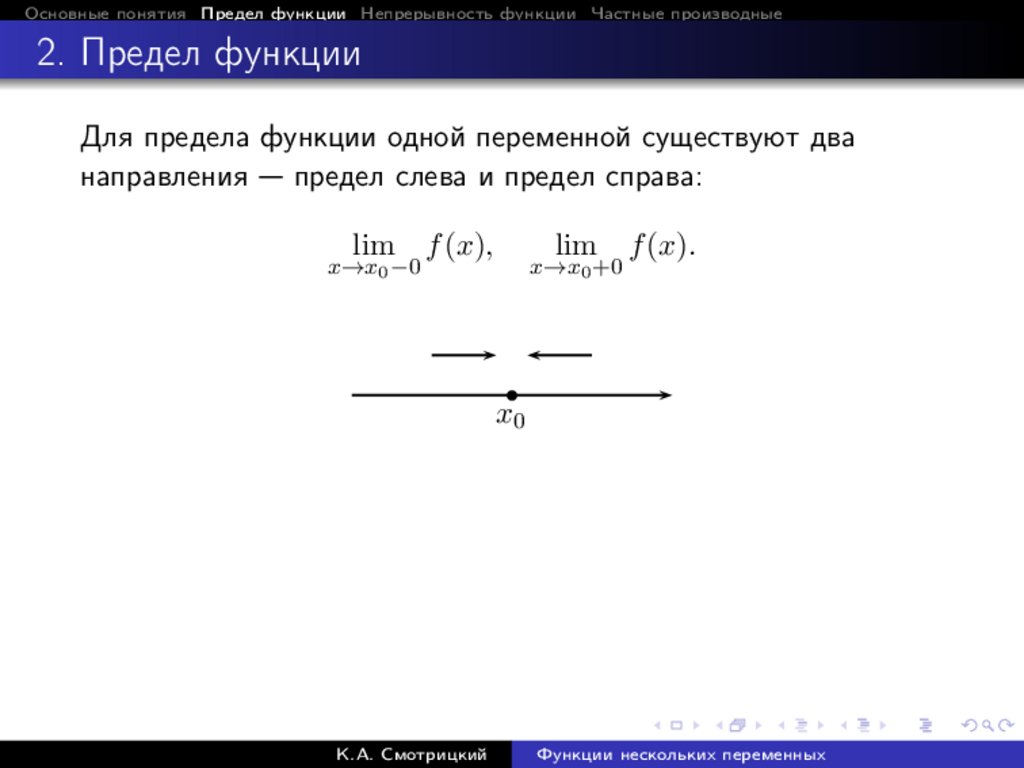
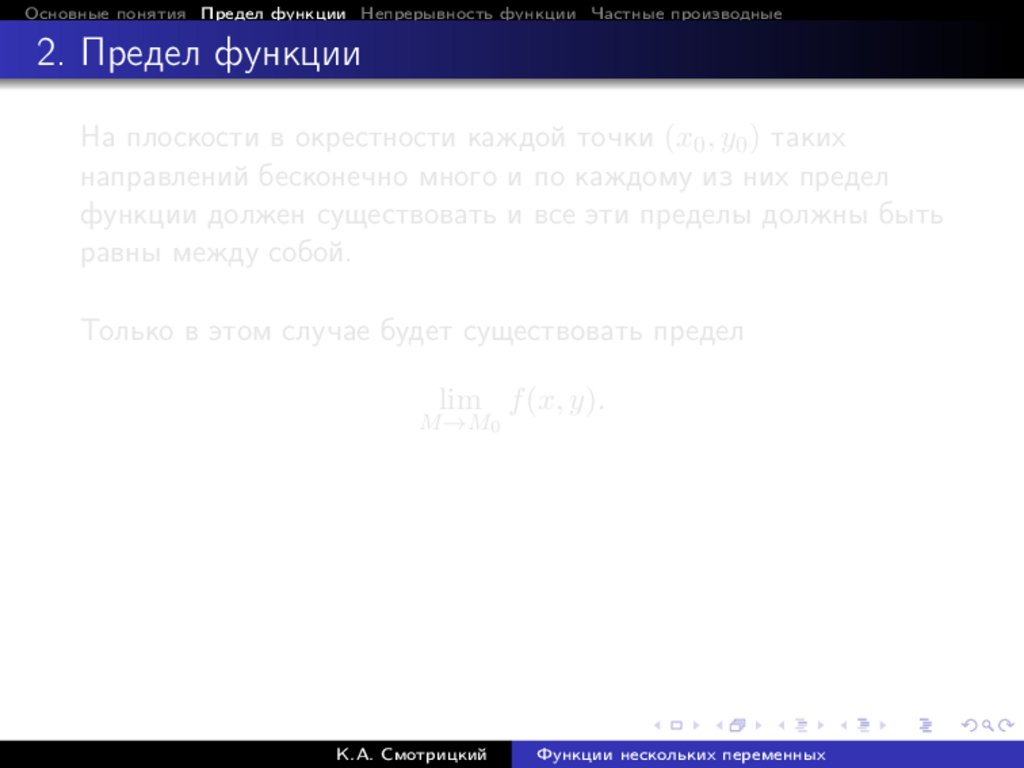










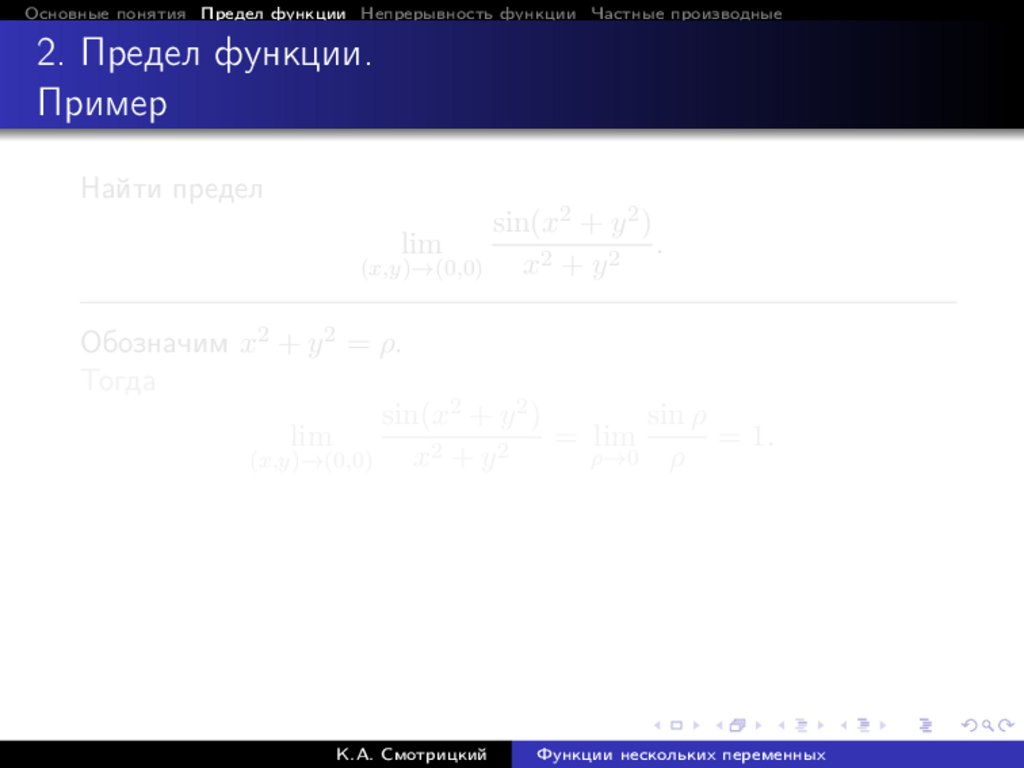
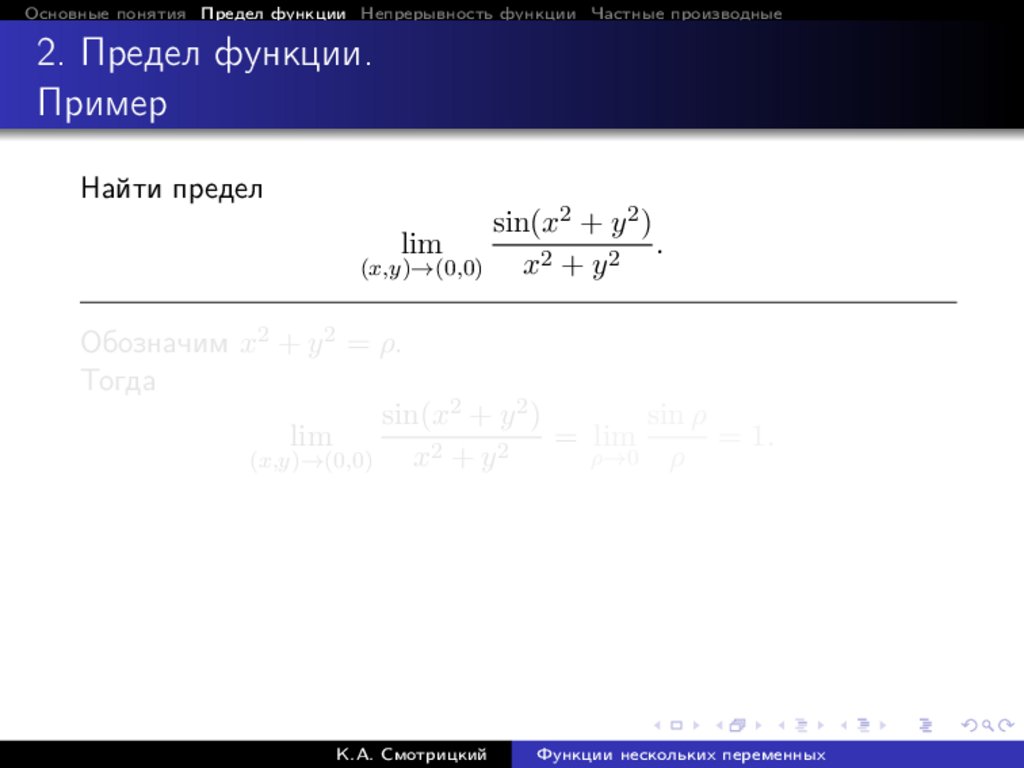
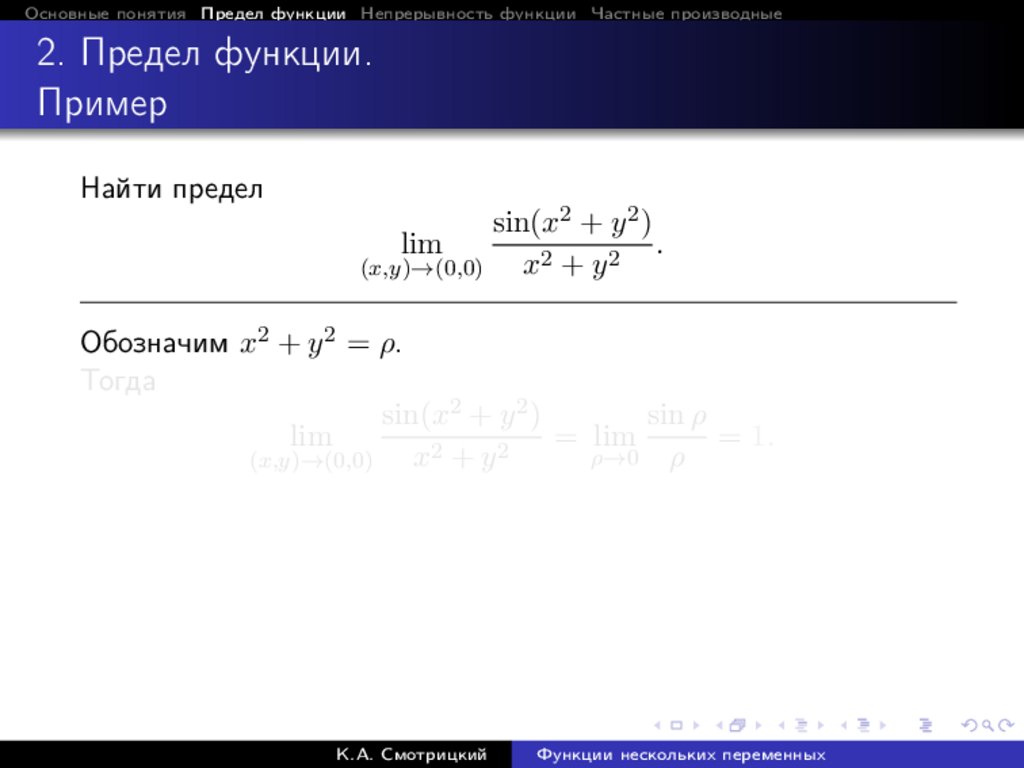



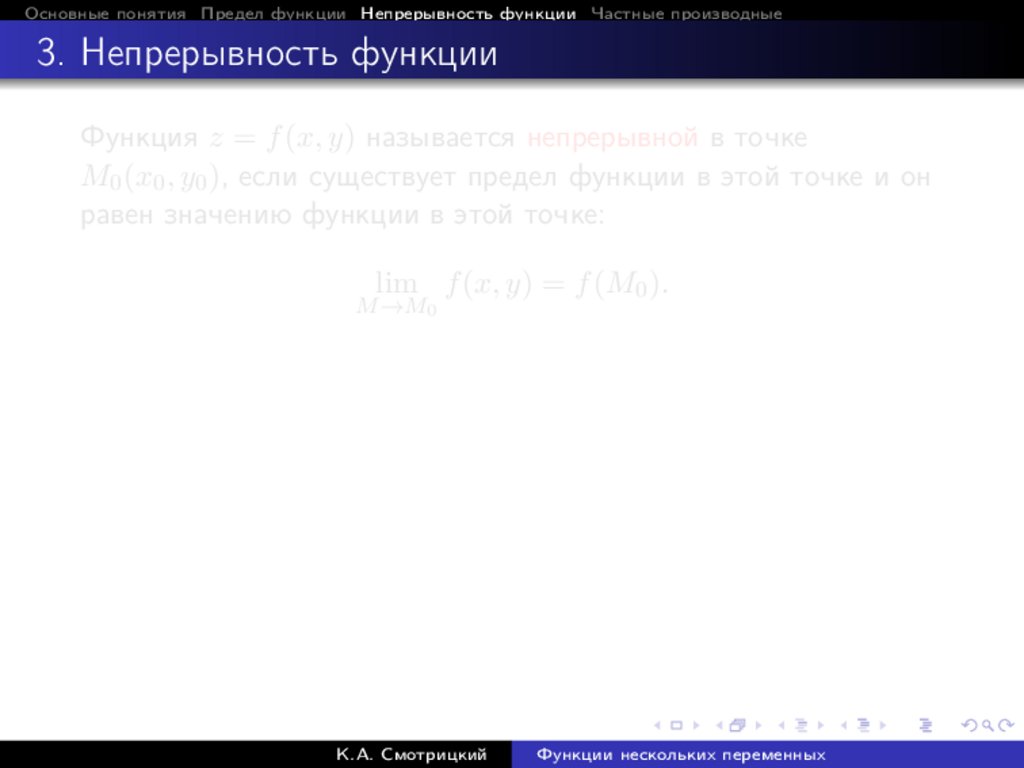
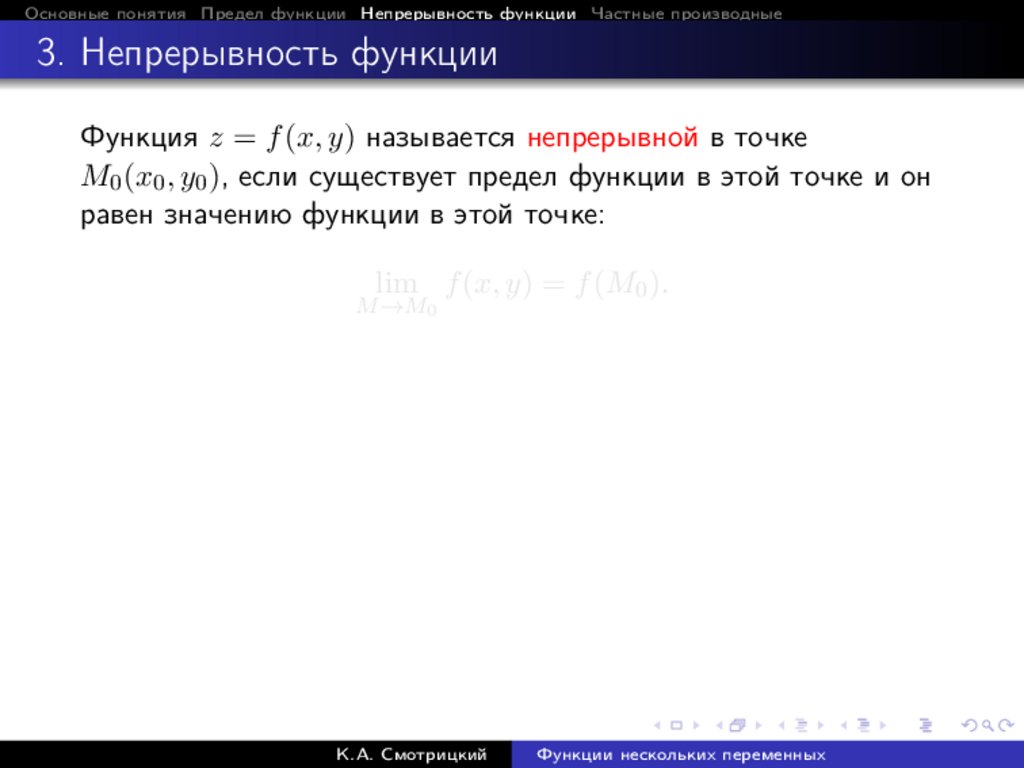

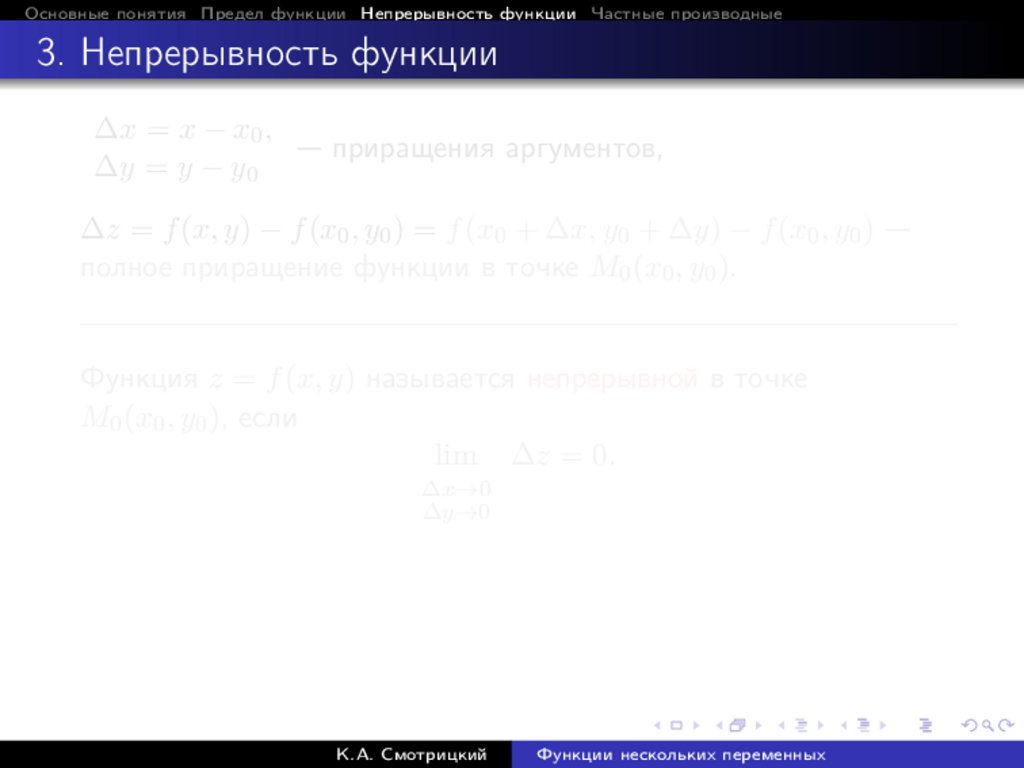
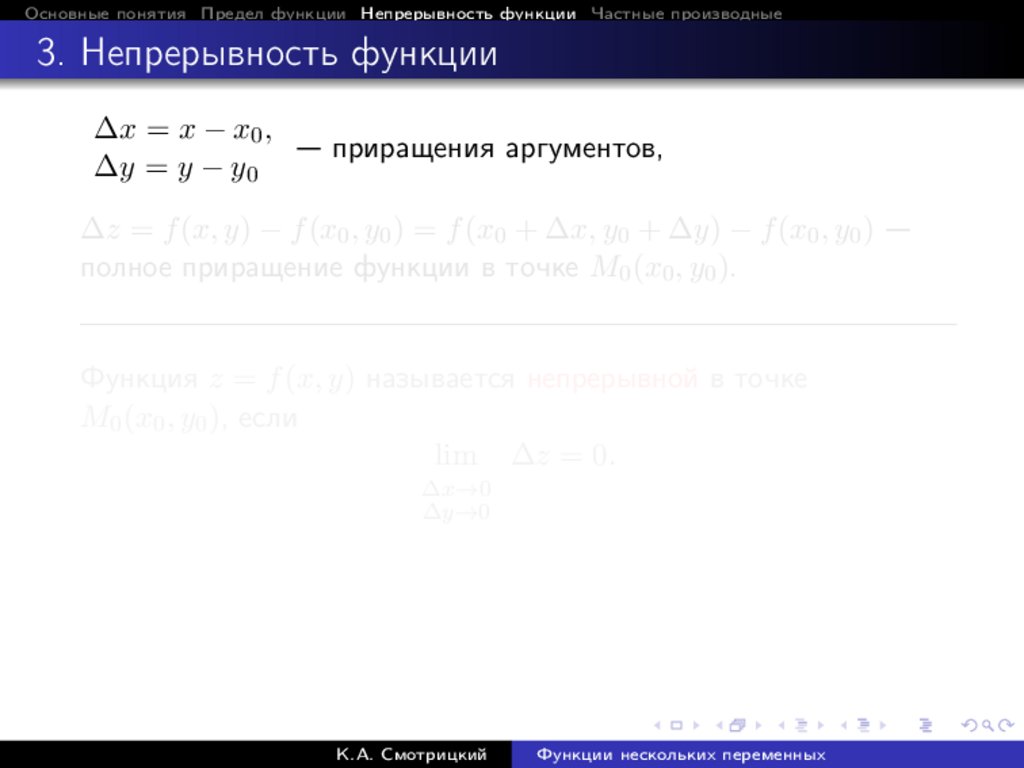

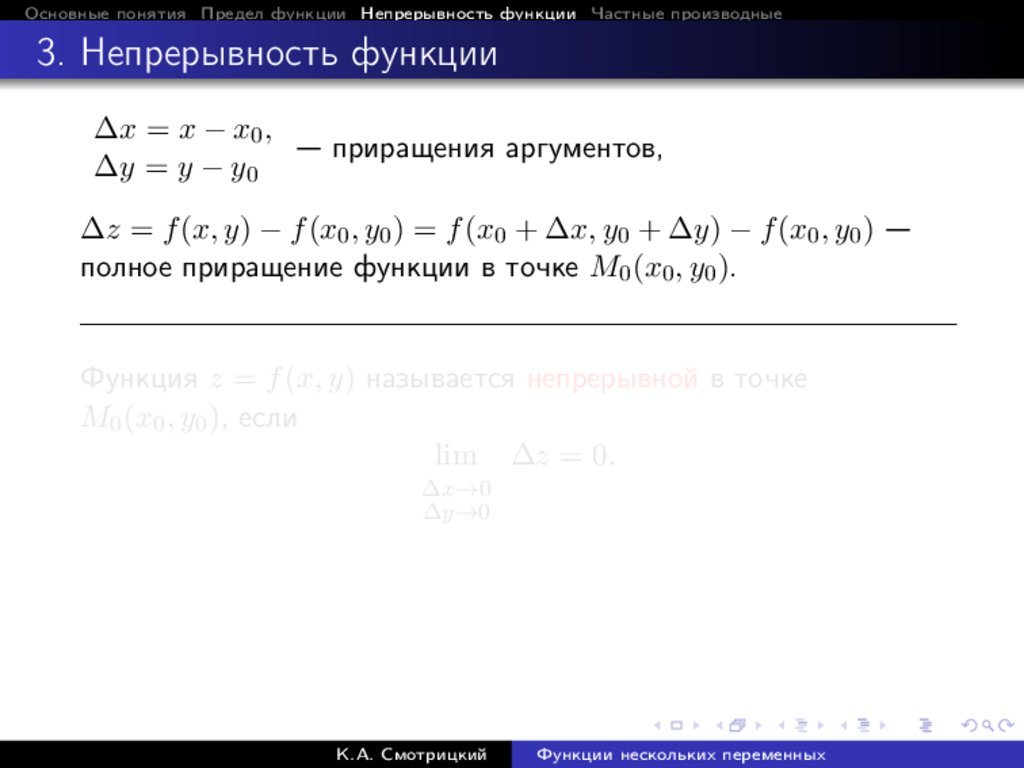

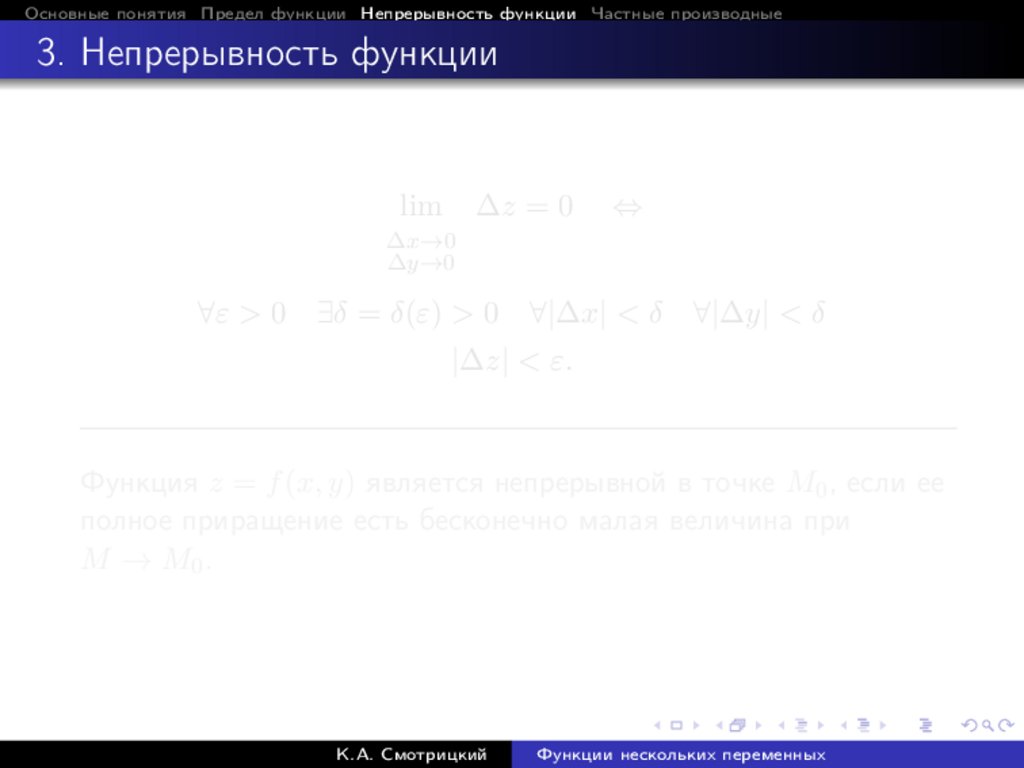
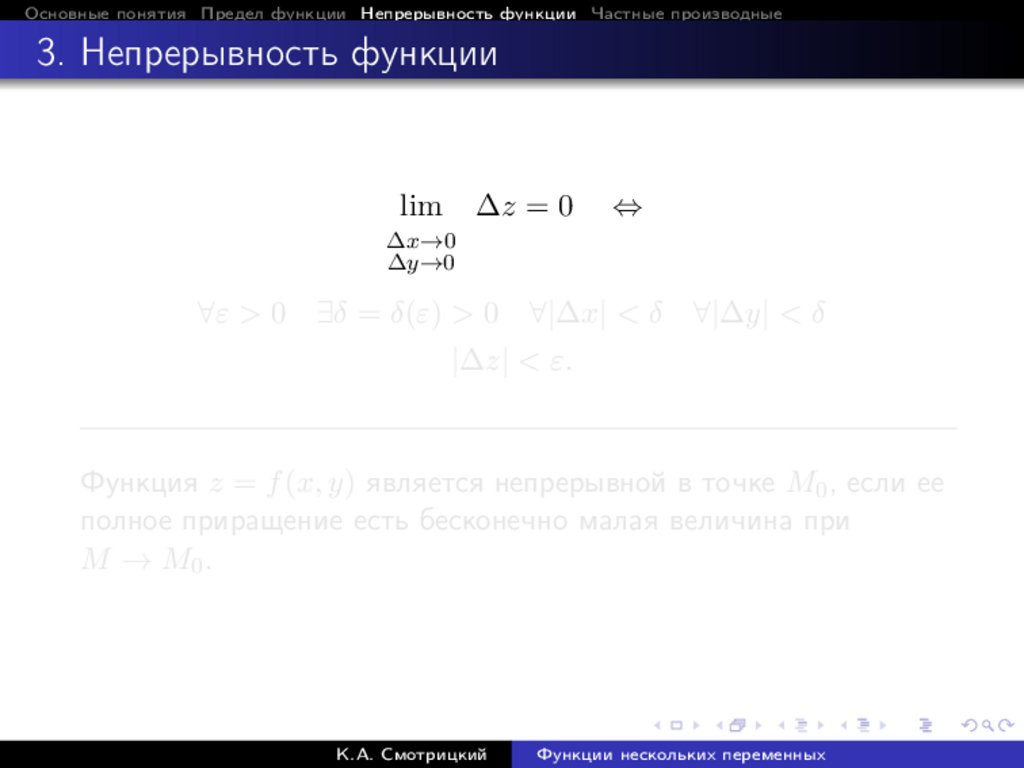
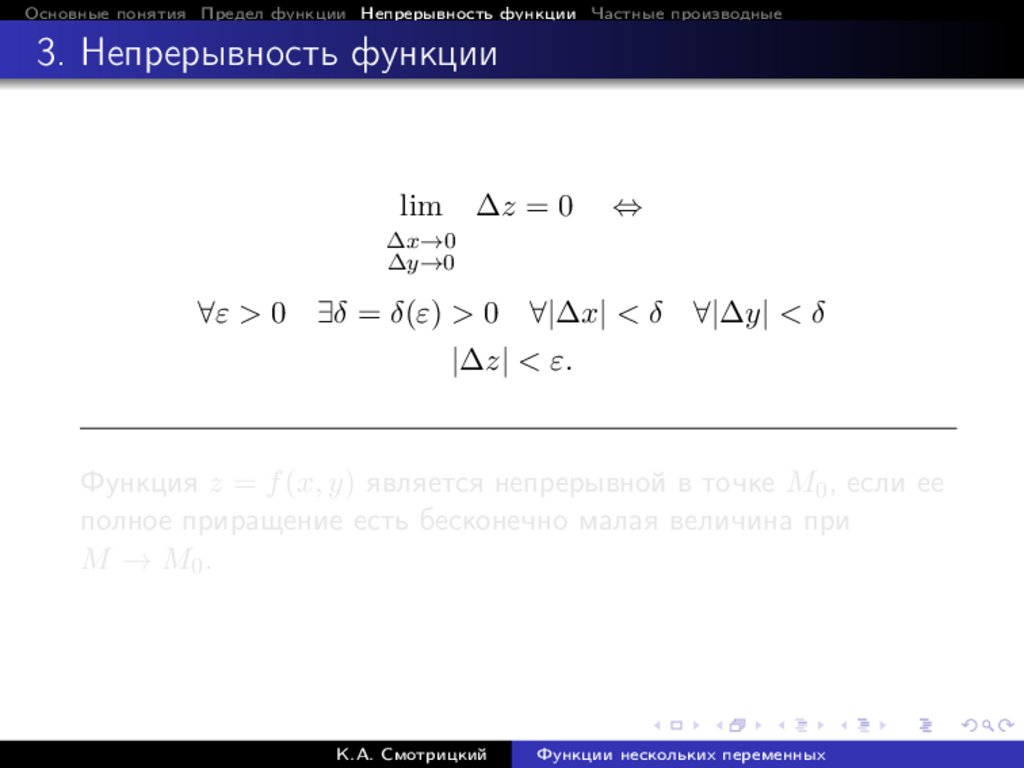

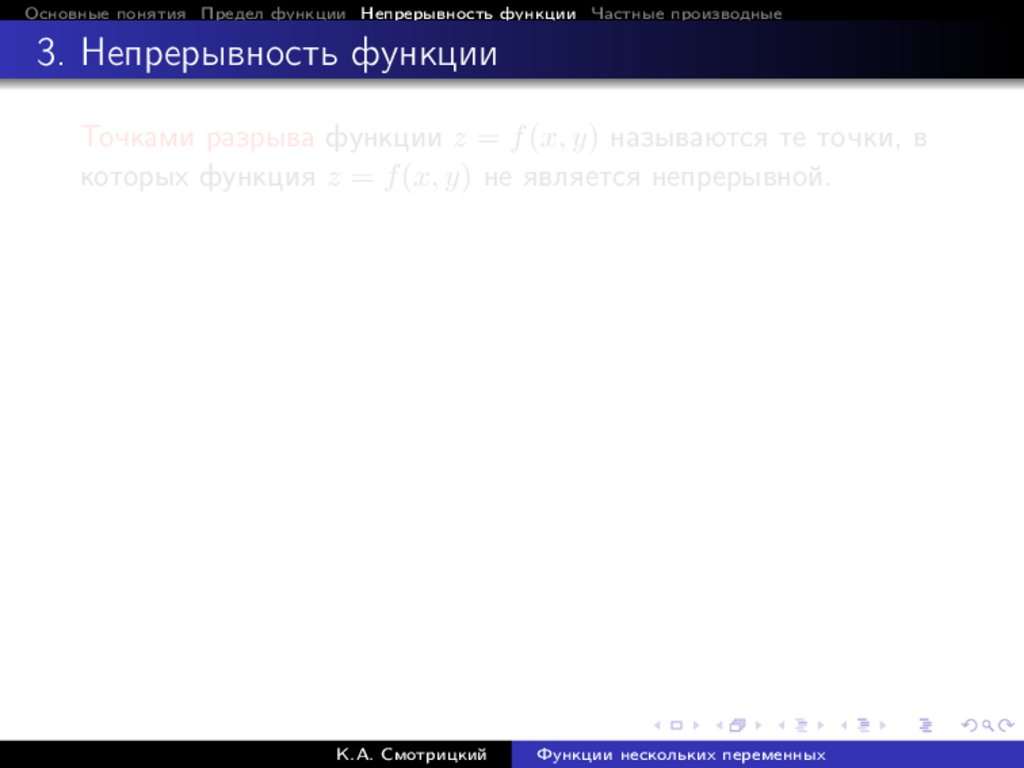
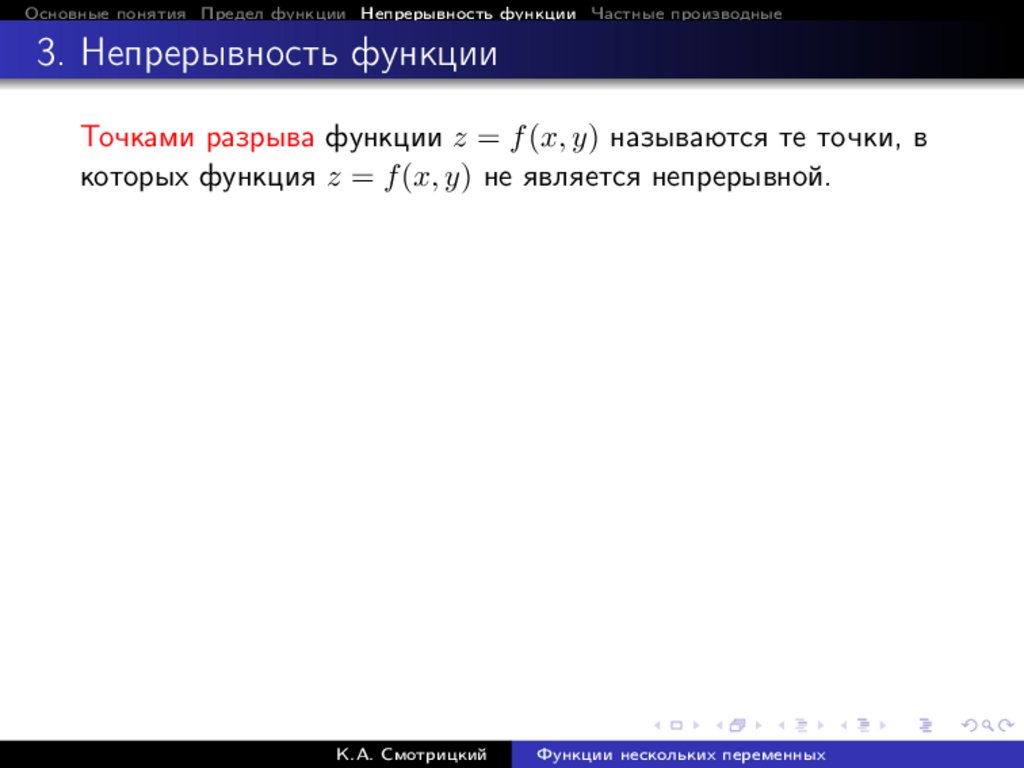
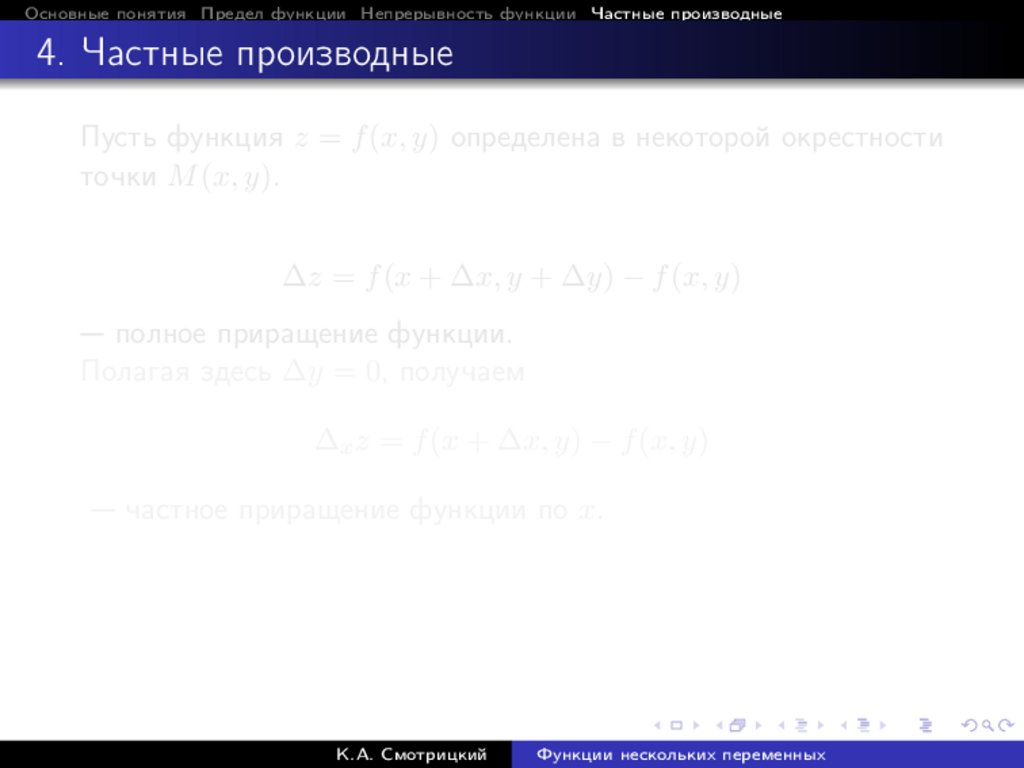
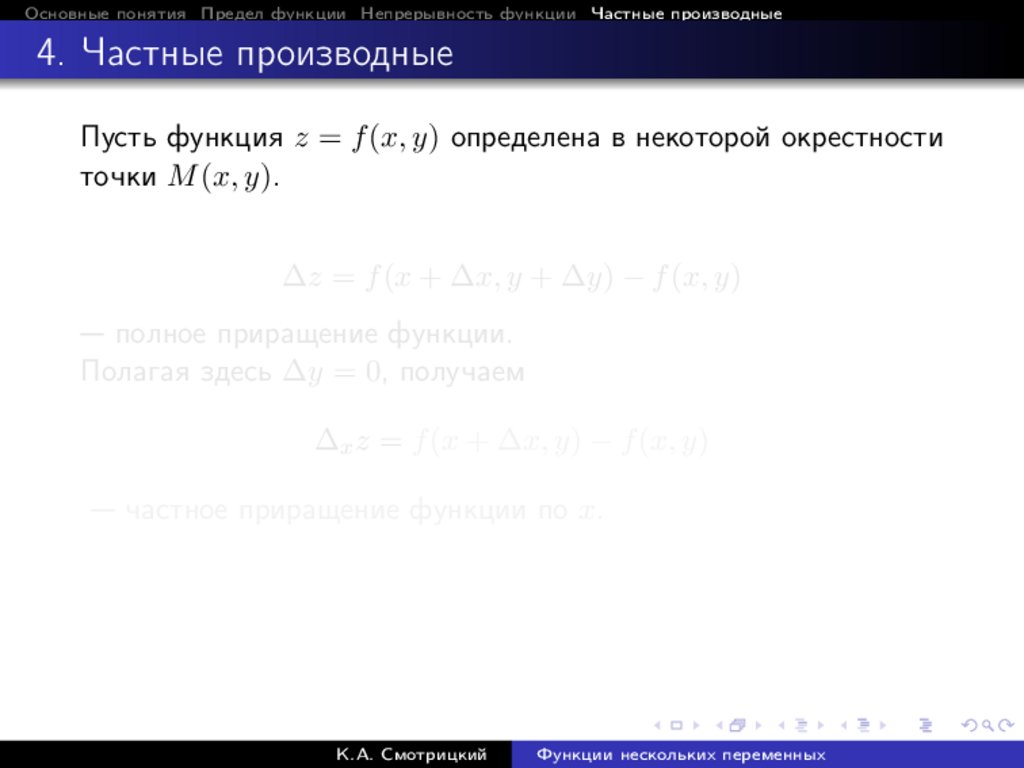




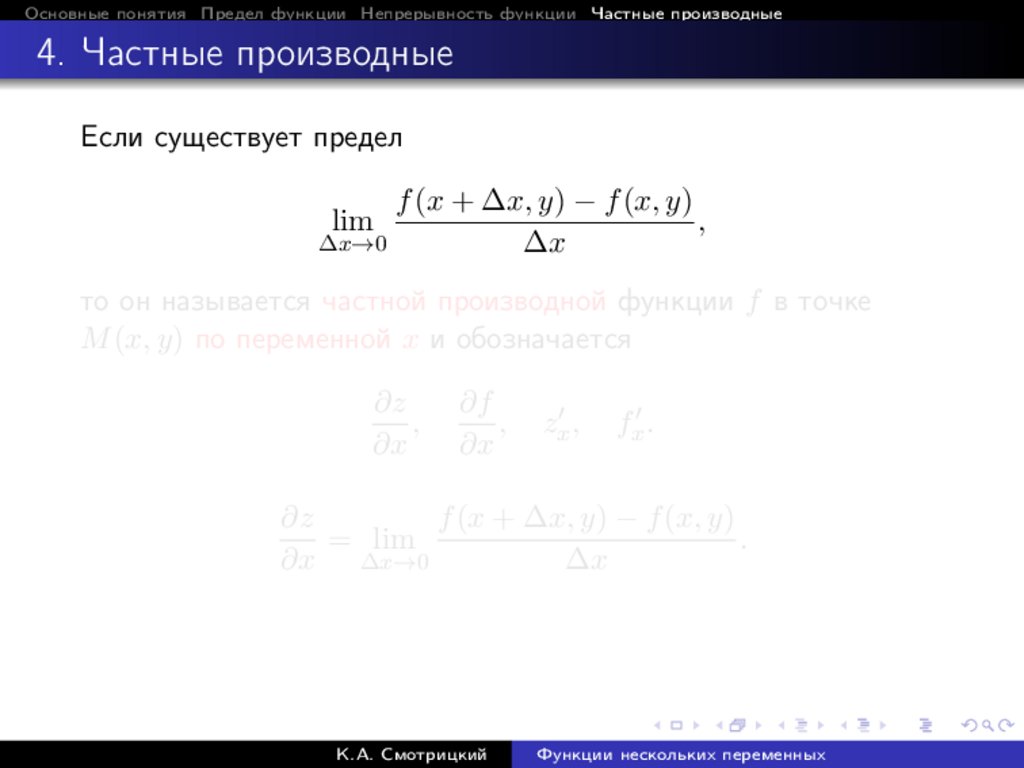
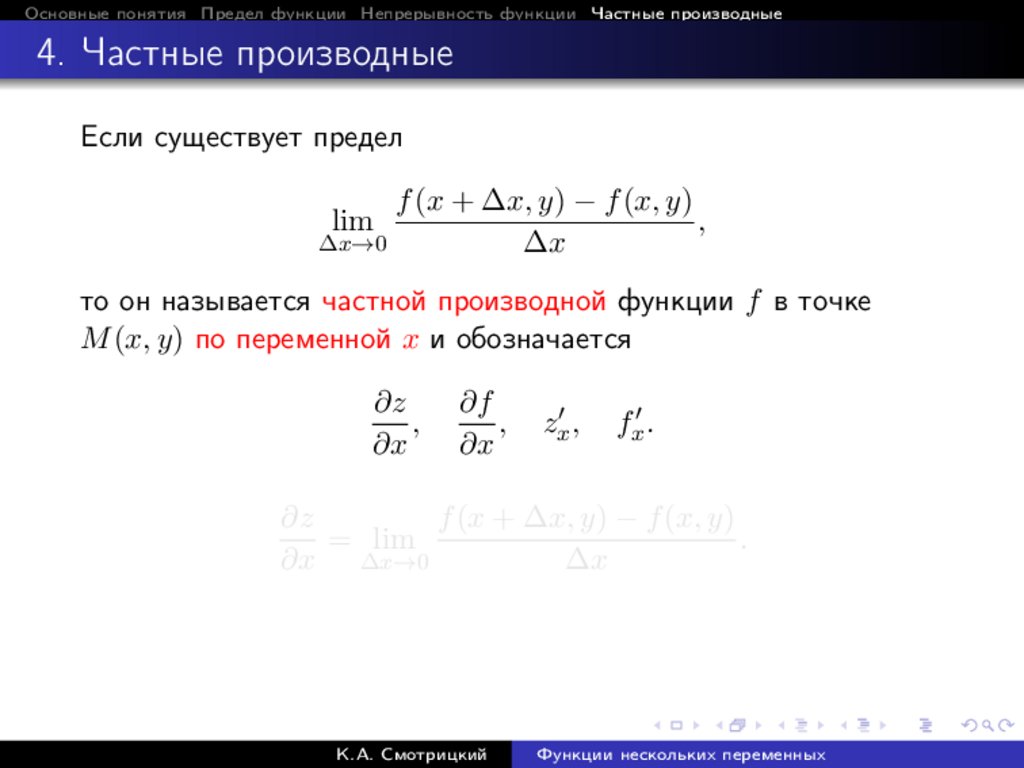

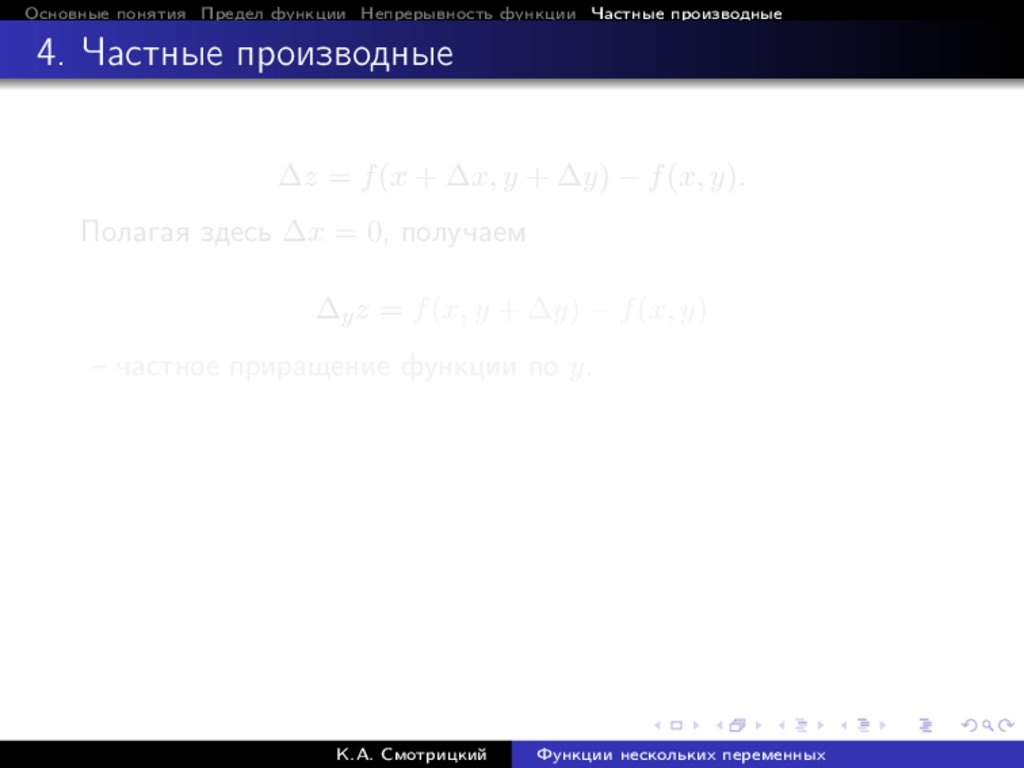
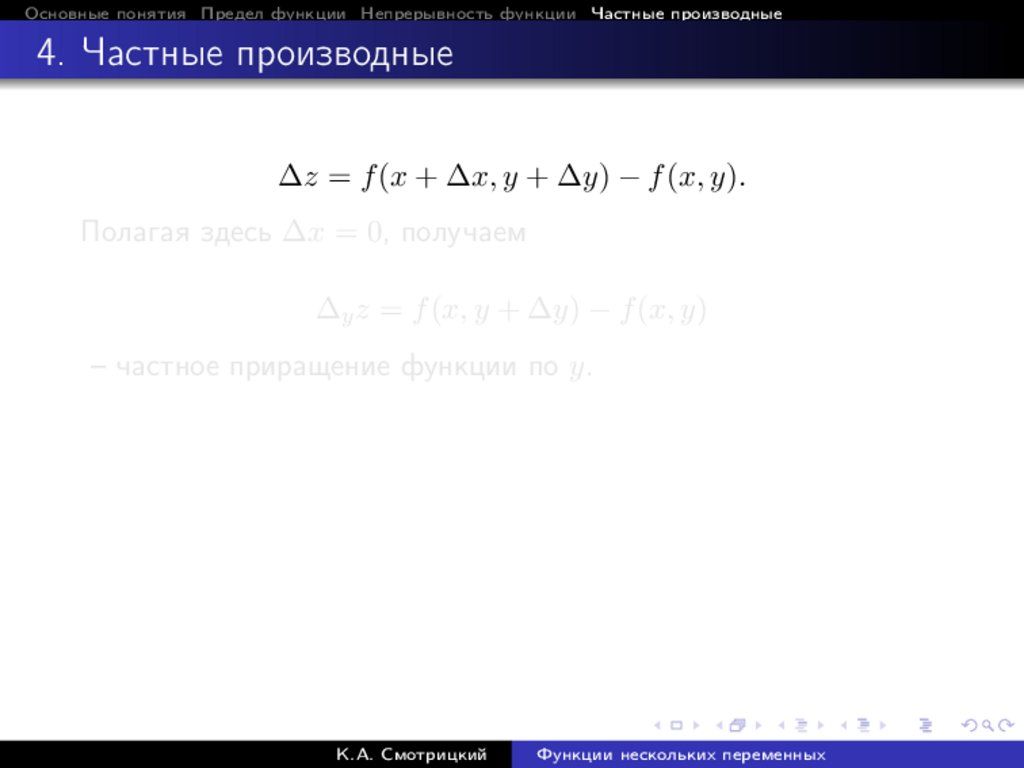


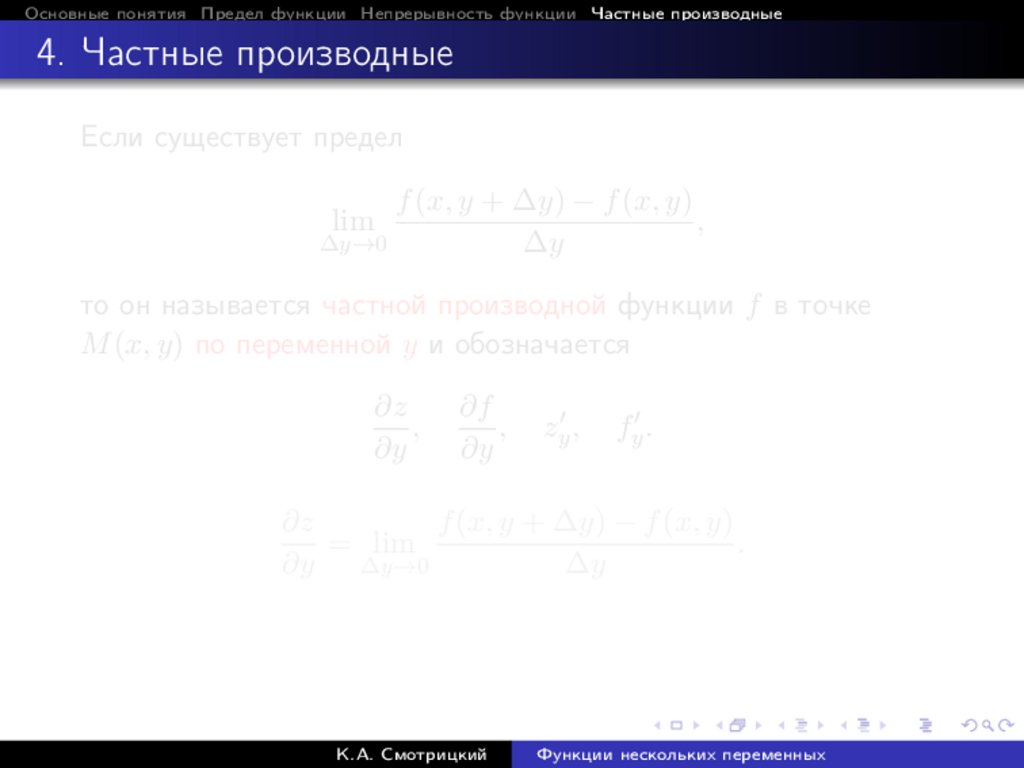
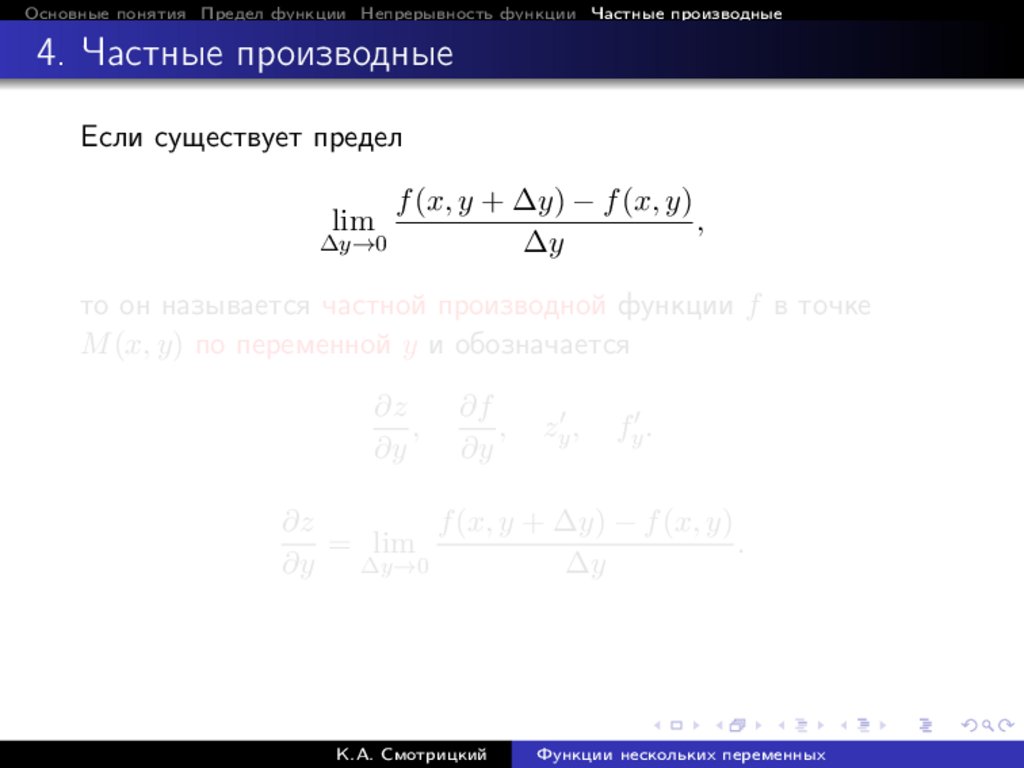


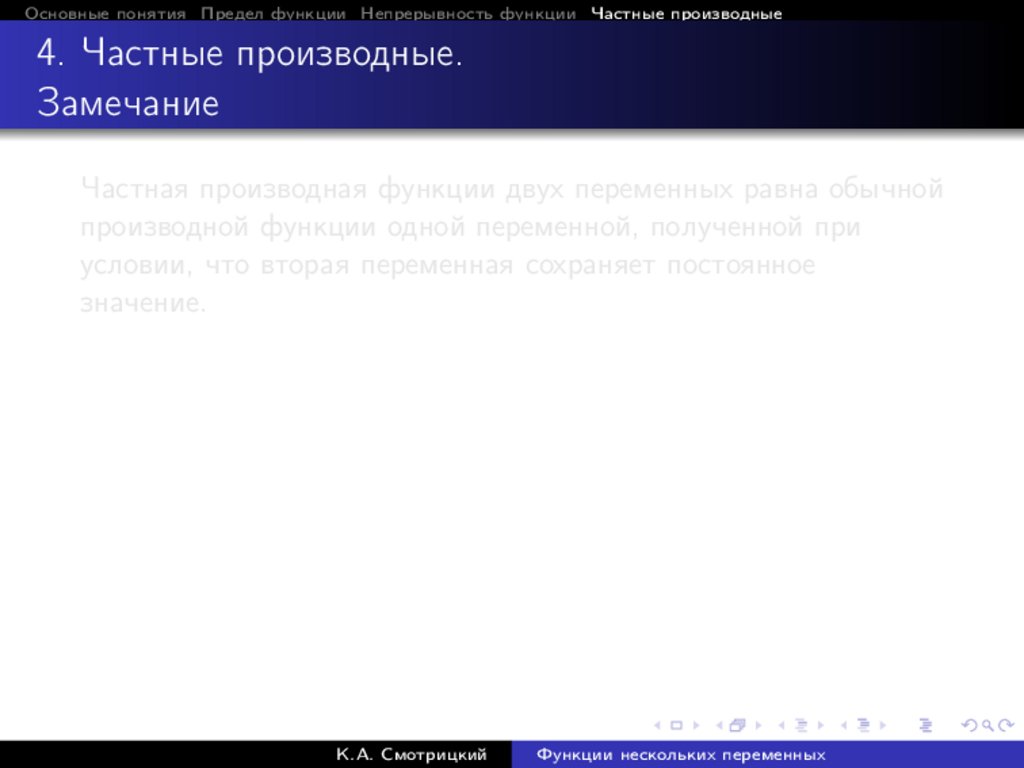
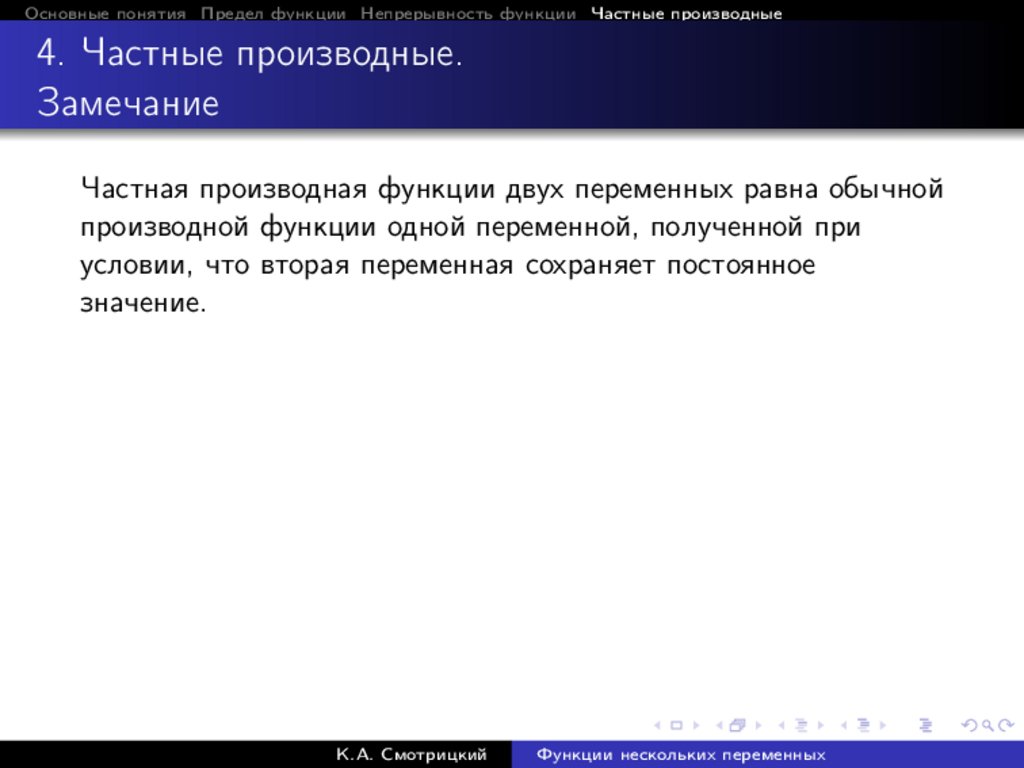
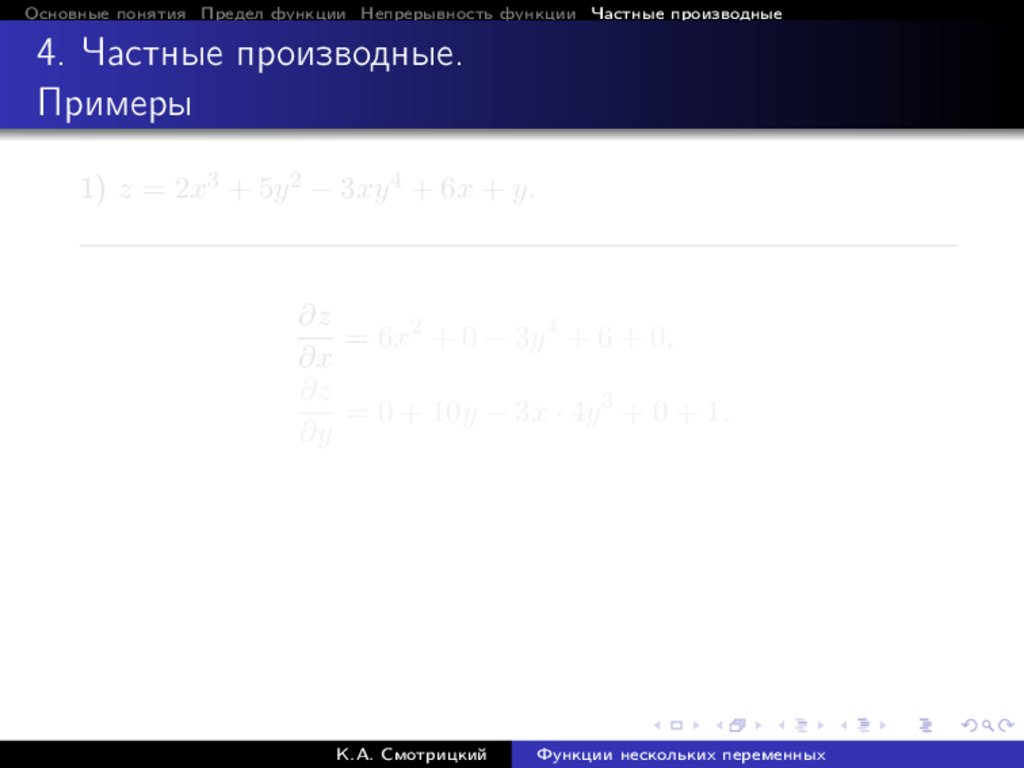
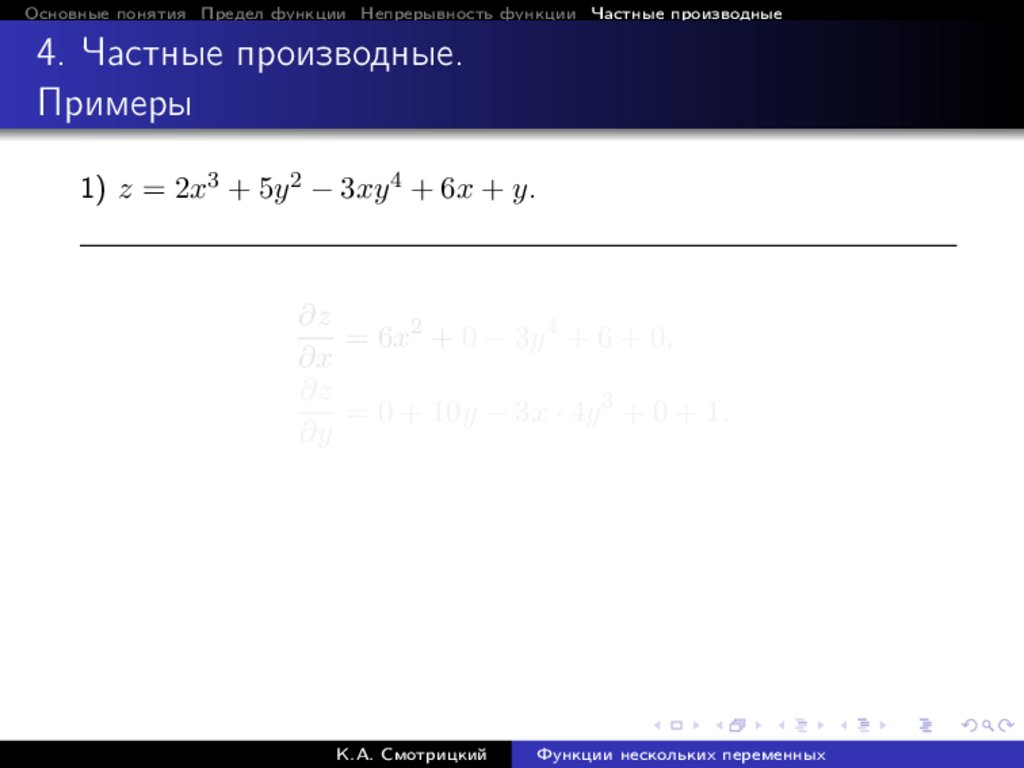





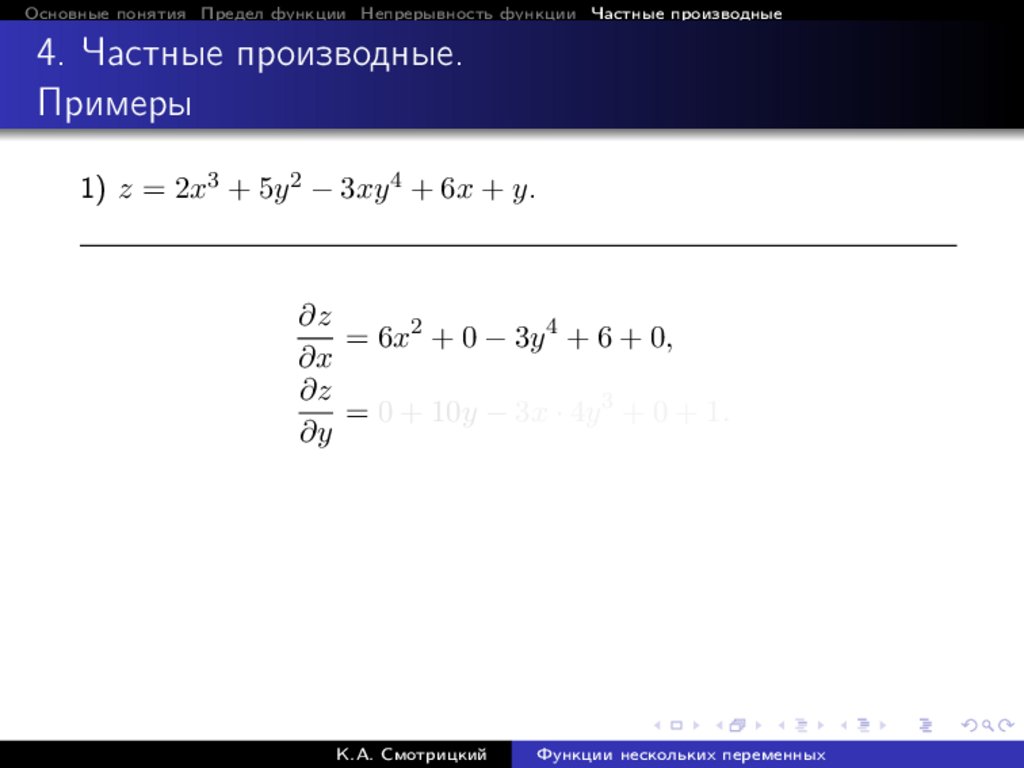
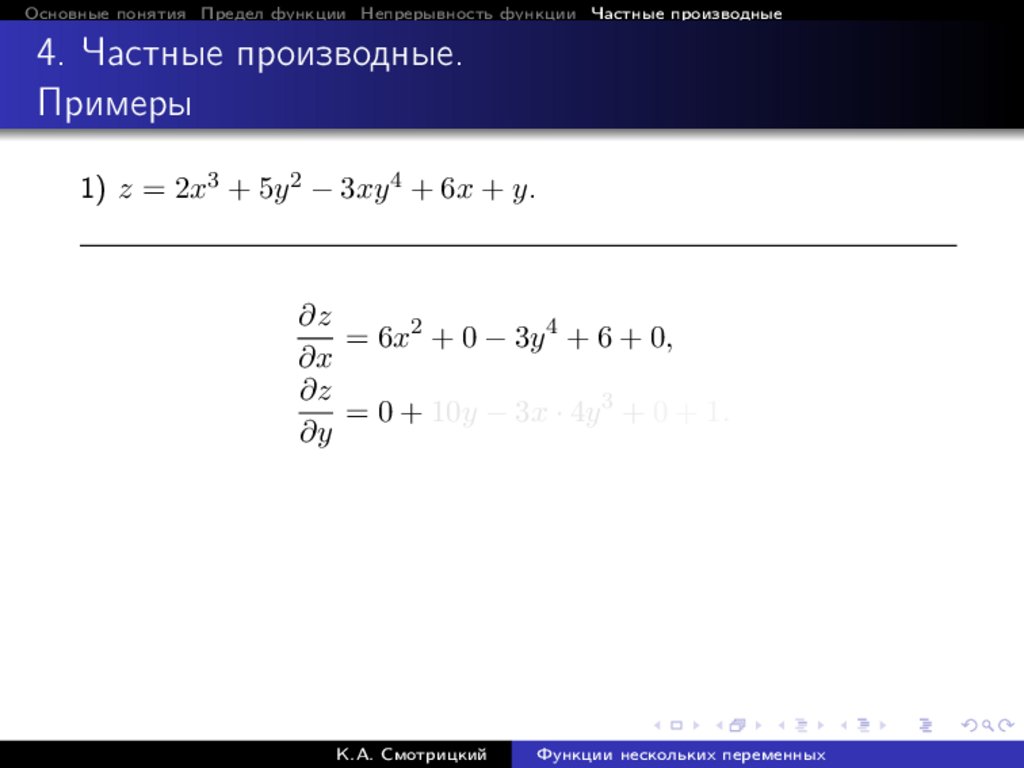





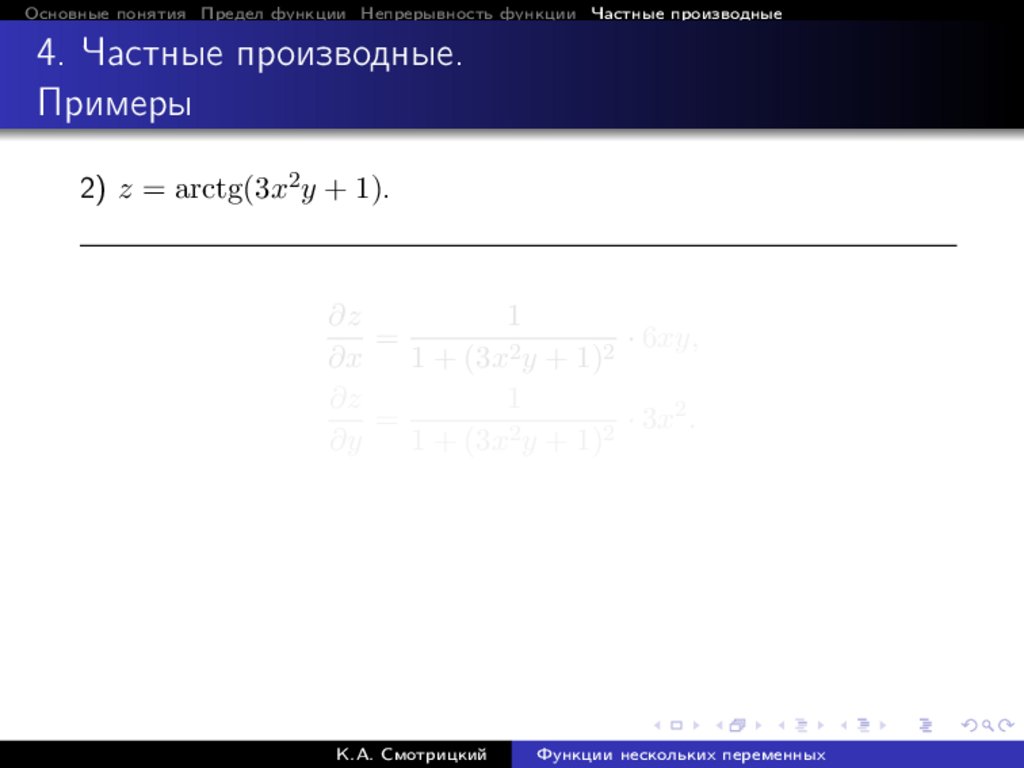
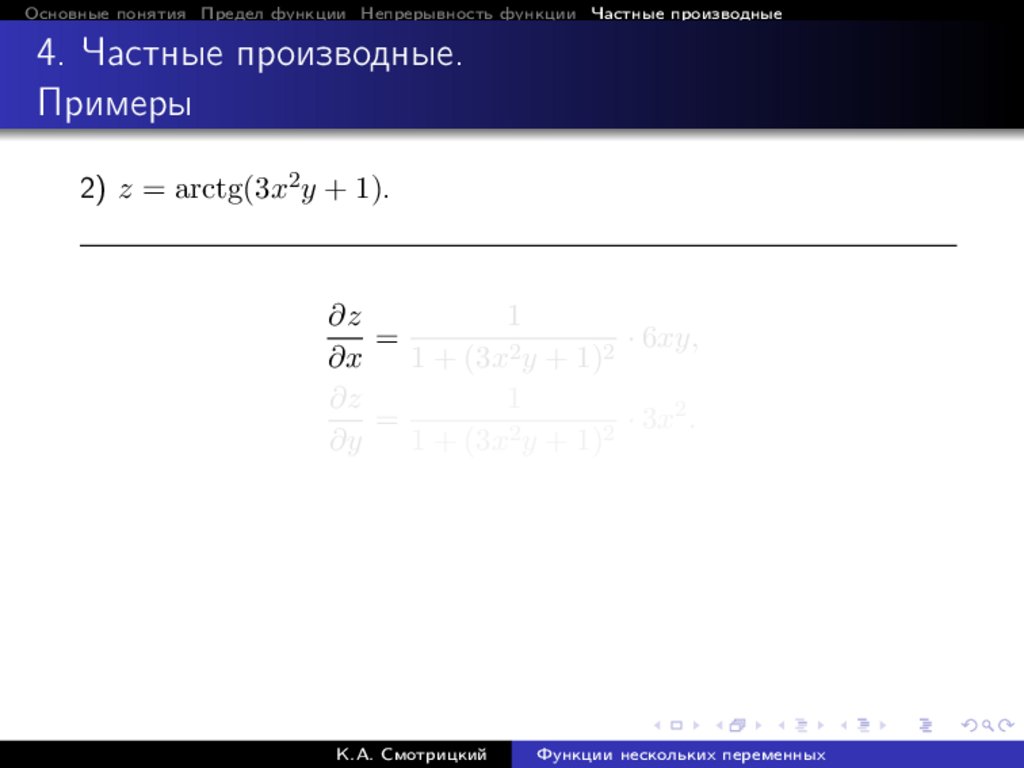
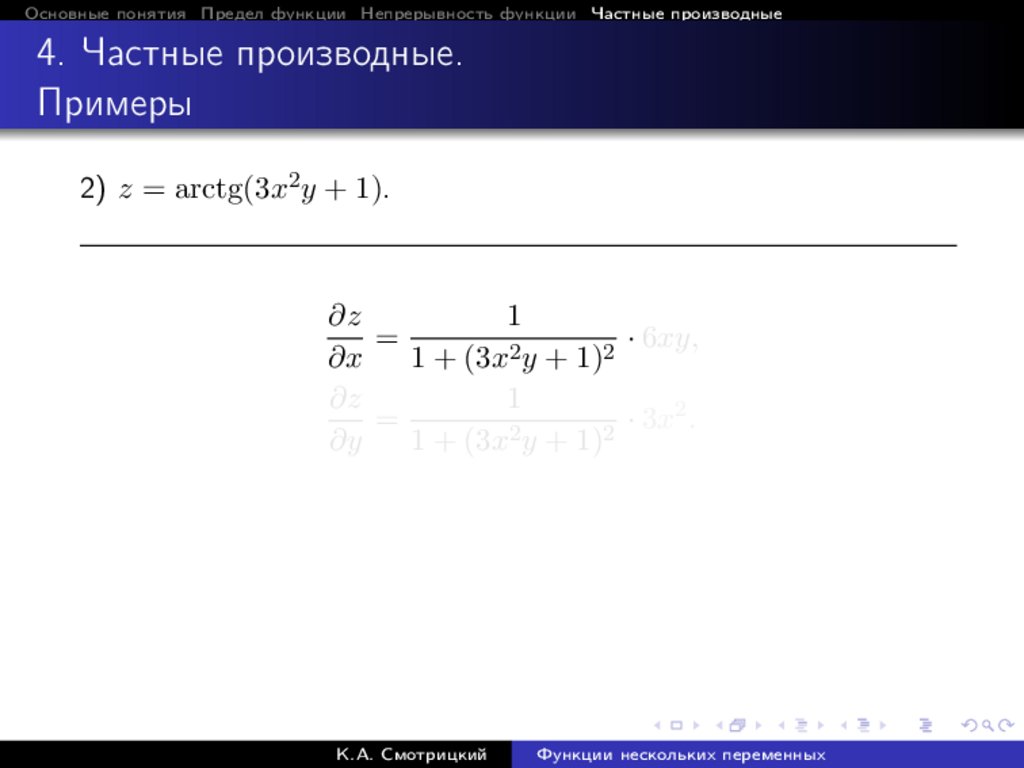
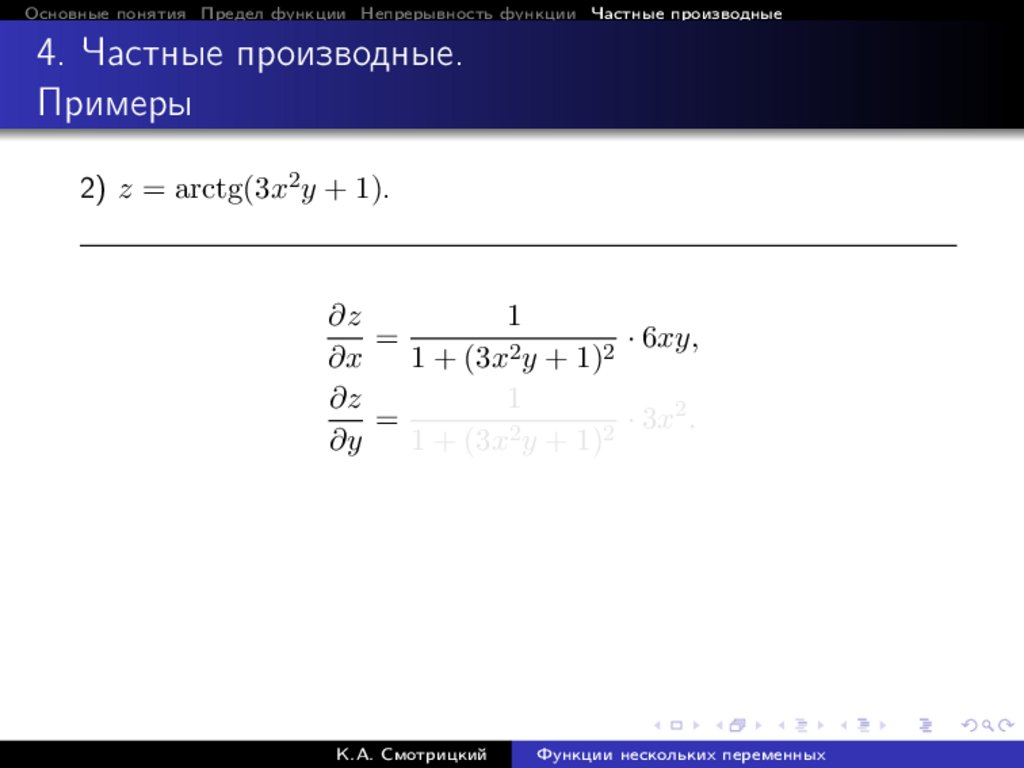
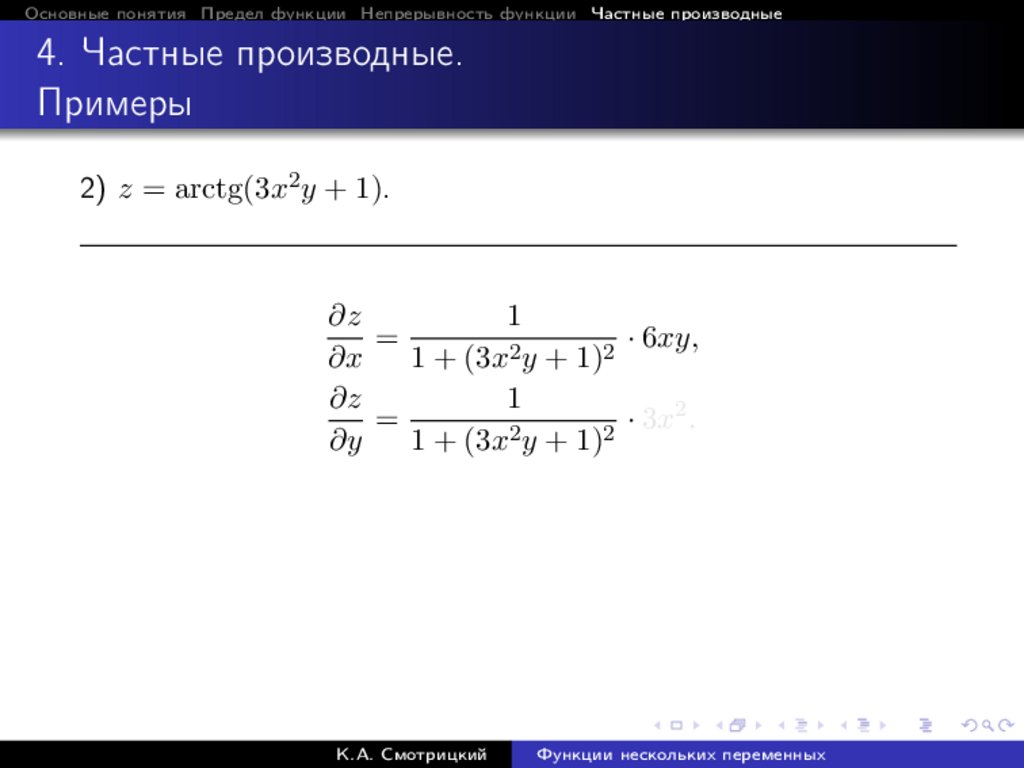

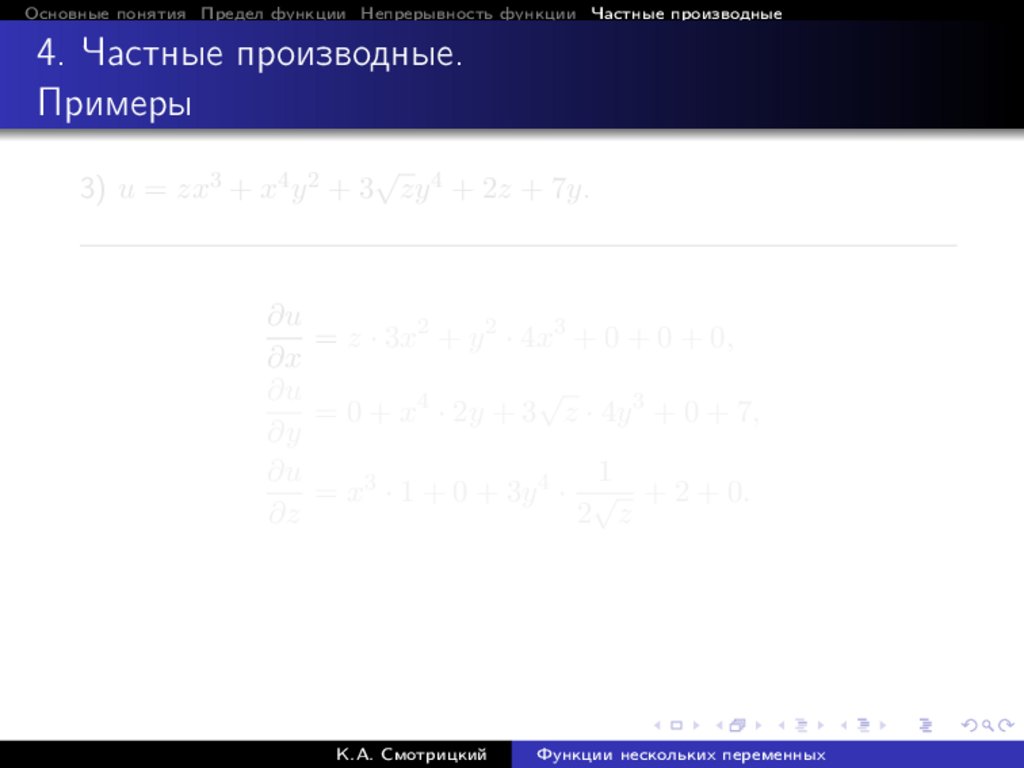


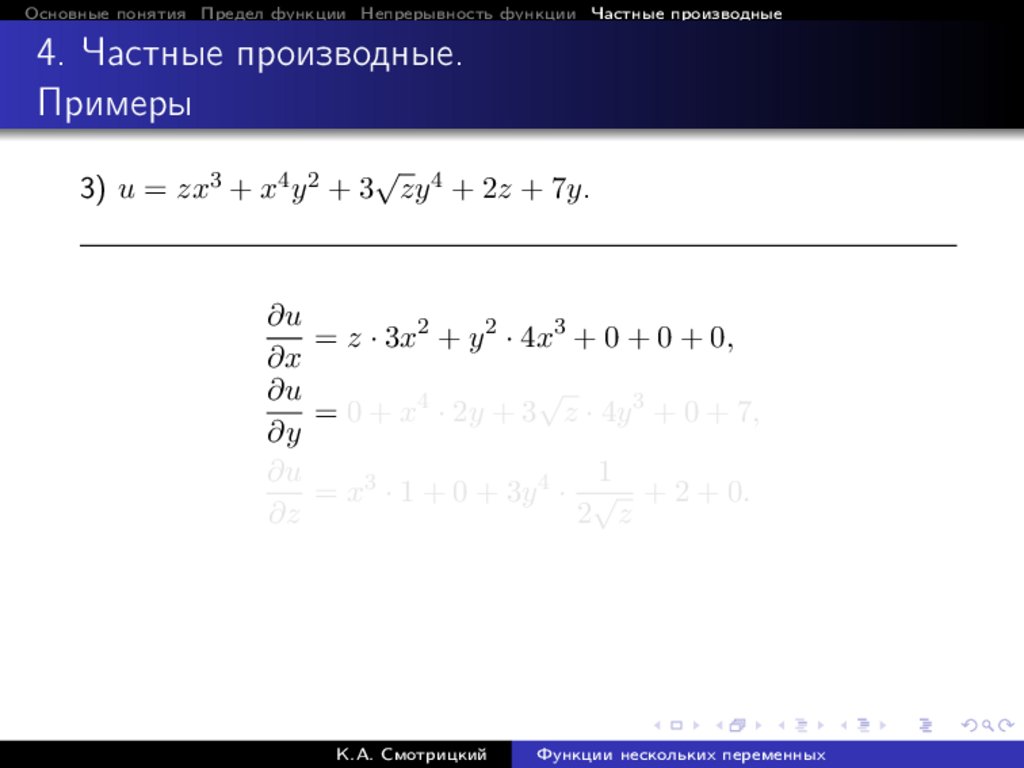
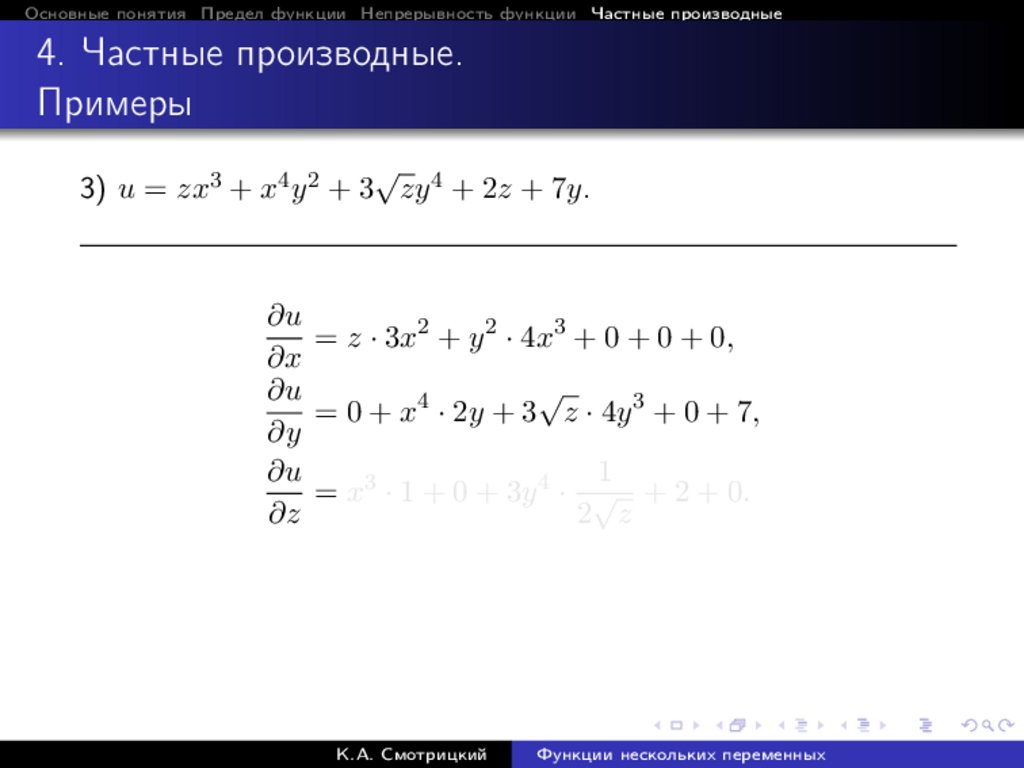


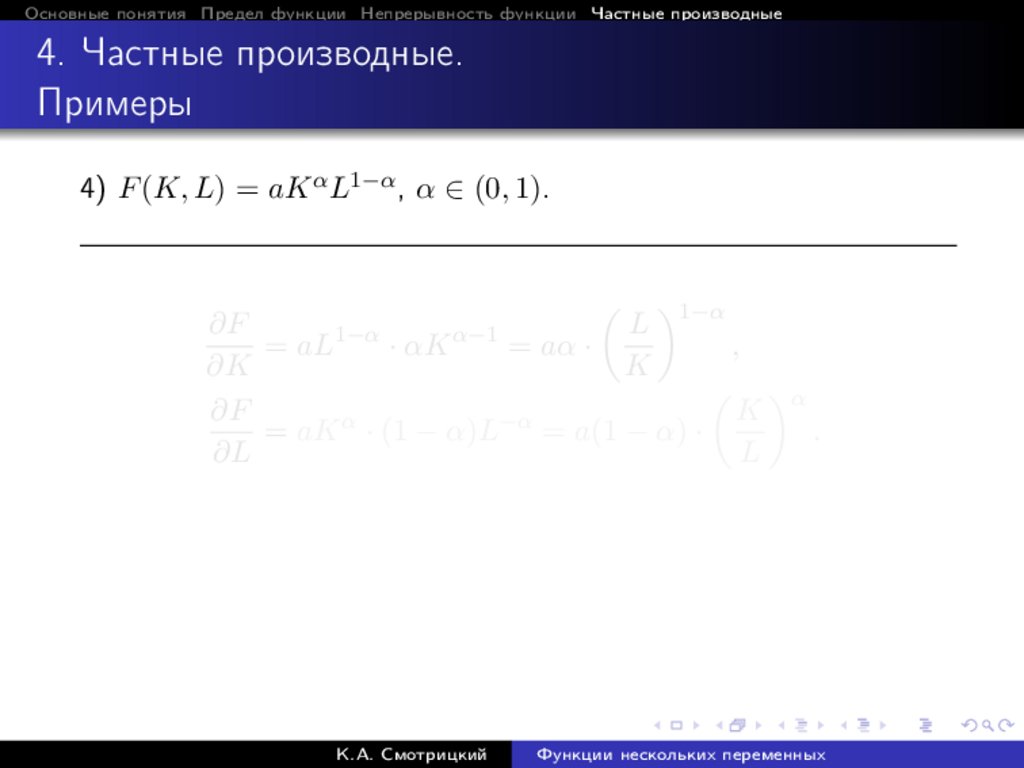
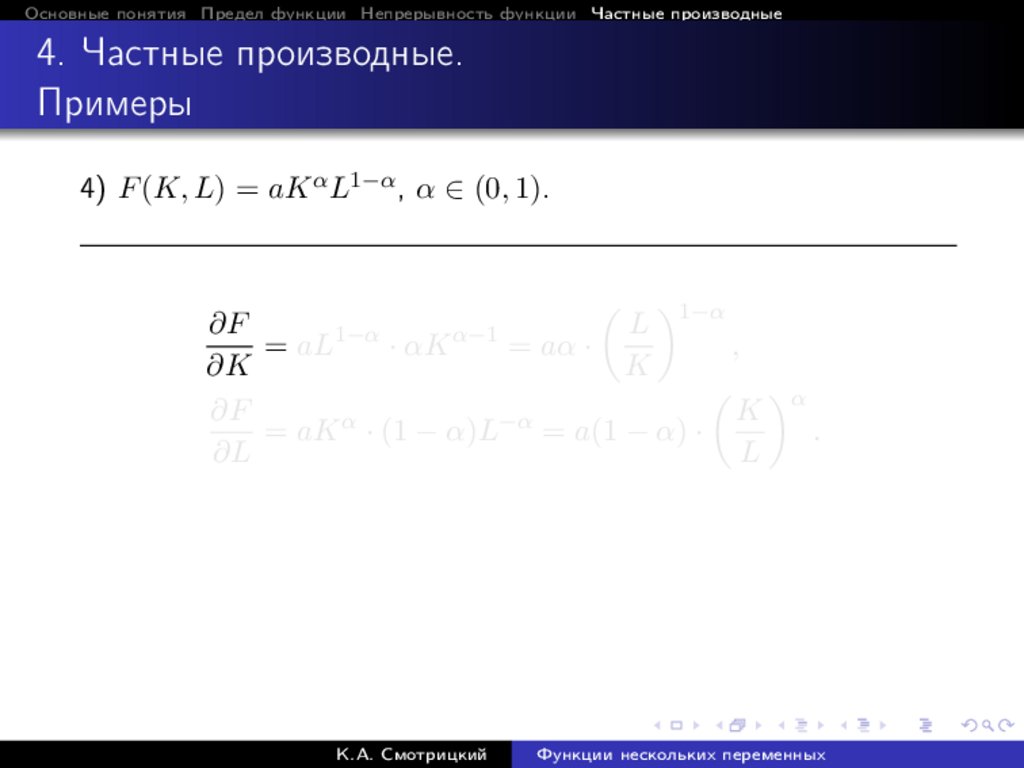
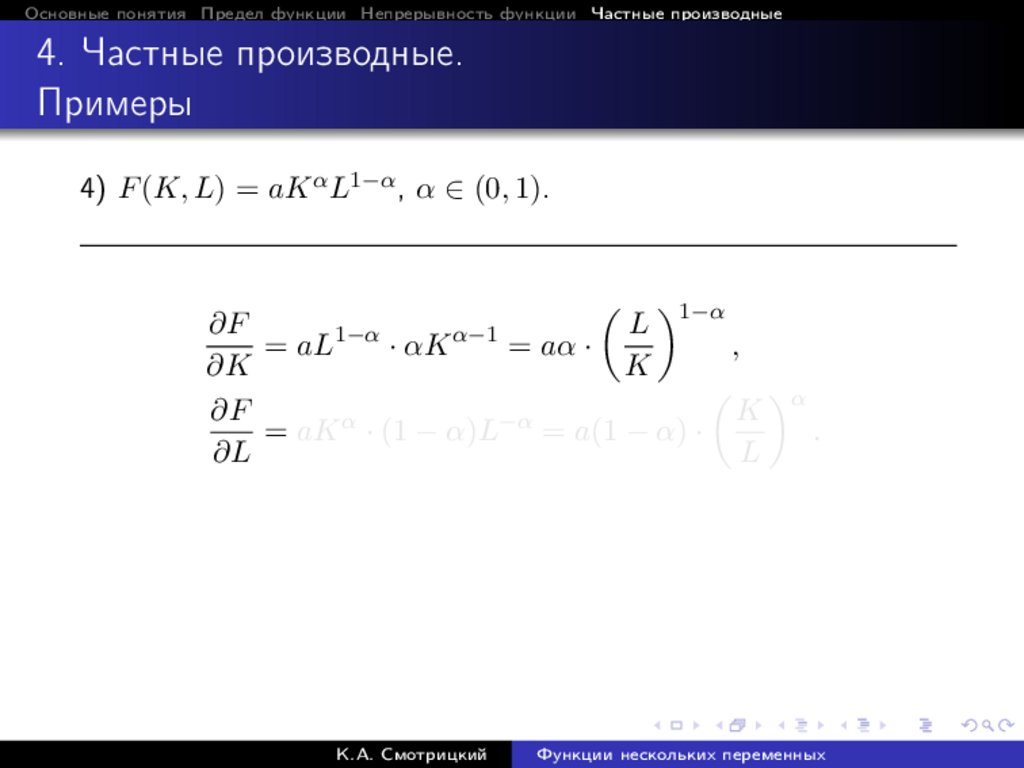

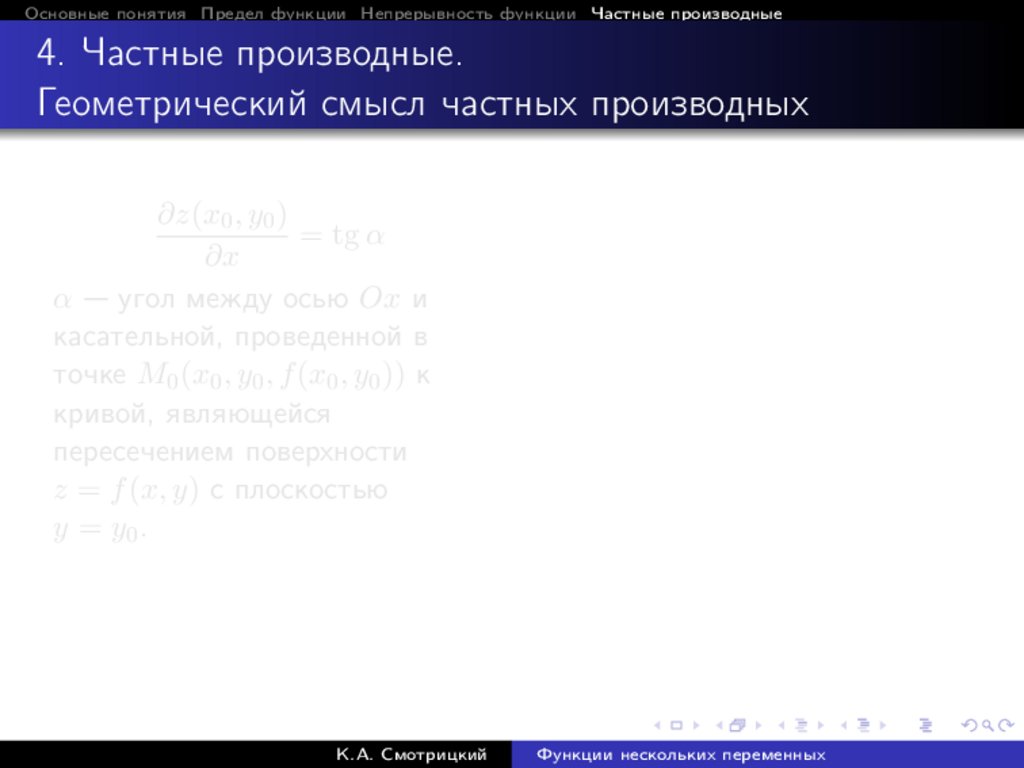
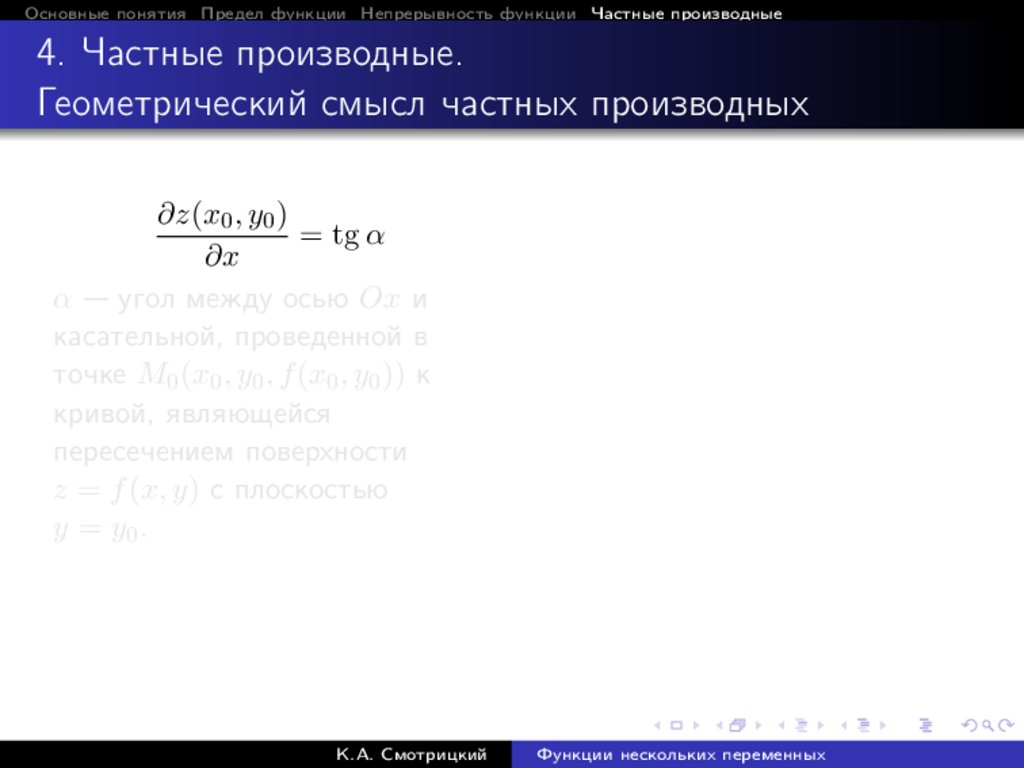



 Математика
Математика








