Похожие презентации:
Интегральные суммы
1. Интегральные суммы
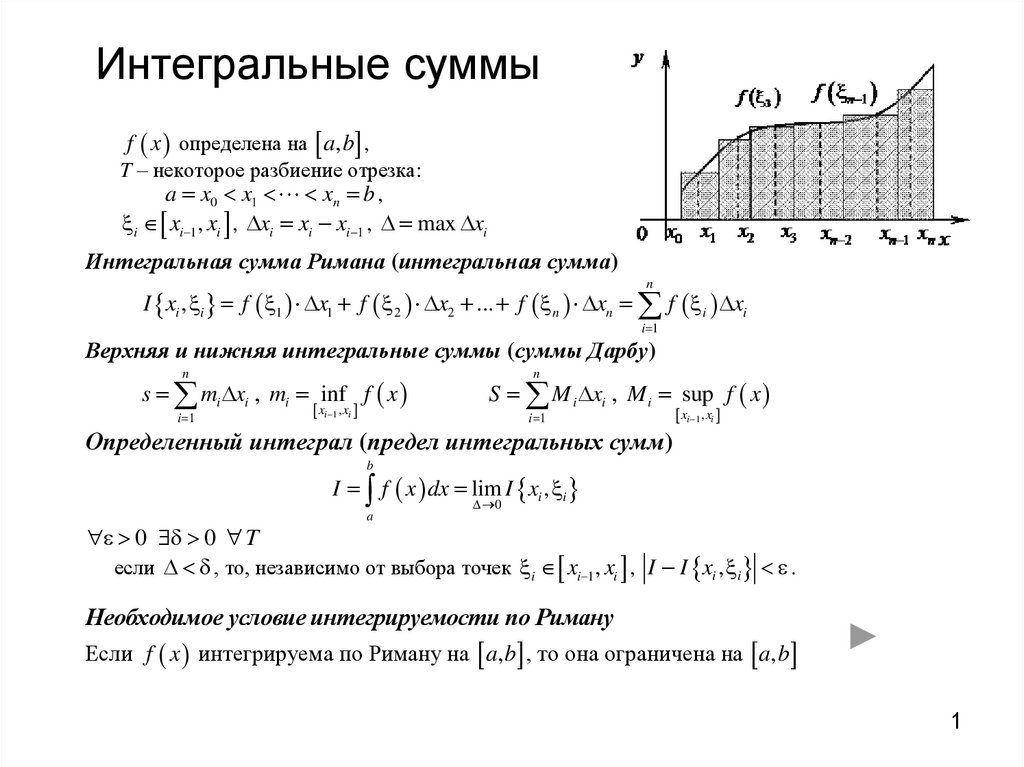
f x определена на a, b ,T – некоторое разбиение отрезка:
a x0 x1 xn b ,
i xi 1 , xi , xi xi xi 1 , max xi
Интегральная сумма Римана (интегральная сумма)
n
I xi , i f 1 x1 f 2 x2 ... f n xn f i xi
i 1
Верхняя и нижняя интегральные суммы (суммы Дарбу)
n
s mi xi , mi inf f x
i 1
xi 1 , xi
n
S M i xi , M i sup f x
i 1
xi 1 , xi
Определенный интеграл (предел интегральных сумм)
b
I f x dx lim I xi , i
a
0
0 0 T
если , то, независимо от выбора точек i xi 1 , xi , I I xi , i .
Необходимое условие интегрируемости по Риману
Если f x интегрируема по Риману на a, b , то она ограничена на a, b
1
2.
Свойства интегральных сумм Дарбуn
s mi xi , mi inf f x
xi 1 , xi
i 1
n
S M i xi , M i sup f x
i 1
xi 1 , xi
1. T 0 точки i на сегментах xi 1 , xi можно выбрать так, что
0 I xi , i s
0 S I xi , i .
Для любого фиксированного разбиения
s inf I xi , i
S sup I xi , i
2. Если T получено из T добавлением k новых точек, то
0 s s M m k
0 S S M m k
3. T T s S
4. Множество нижних сумм s функции f x для всевозможных разбиений сегмента a, b
ограничено сверху, а множество верхних сумм S ограничено снизу.
5. I I , где I inf S , I sup s – верхний и нижний интегралы Дарбу.
6. Лемма Дарбу.
lim S I , lim s I .
0
0
4
3.
Классы функций интегрируемых по Риману на a, bНеобходимое условие : ограниченность на a, b .
mi inf f x
Необходимое и достаточное условие (Теорема Римана)
n
0 T S s i xi .
i 1
xi 1 , xi
M i sup f x
xi 1 , xi
i M i mi –
колебание f x на xi 1 , xi
Достаточные условия:
1. Непрерывность на a, b .
2. f x определена и ограничена на a, b и 0 можно указать конечное
число интервалов, покрывающих все точки разрыва этой функции и имеющих
общую сумму длин меньше .
2.1. f x определенна и ограниченна на a, b и имеет лишь конечное
число точек разрыва.
2.2. f x отличается от интегрируемой на a, b функции лишь в
конечном количестве точек
(Интегралы от таких функций равны)
3. f x определенна и монотонна на a, b .
9


 Математика
Математика








