Способы решения квадратных уравнений

1. Муниципальное бюджетное общеобразовательное учреждение Щебетовская школа им.М.А.Македонского г.Феодосия Республика Крым Проект

по теме:
Выполнил ученик 9-А класса Яценко Владимир
Руководитель: учитель математики Гордиенок Татьяна Викторовна
2023 год

2.

Актуальность:
Современные научно-методические исследования показывают,
что использование разнообразных методов и способов
позволяет значительно повысить эффективность и качество
изучения решений квадратных уравнений.
Цель:
Разработать методическое пособие для учащихся, содержащее
различные способы решения квадратных уравнений, выделить
эффективные способы решения и показать их практическое
применение.
Задачи:
1)Изучить историю развития квадратных уравнений
2)Рассмотреть стандартные и нестандартные методы
решения квадратных уравнений
3)Выявить наиболее удобные способы решения квадратных
уравнений
4)Составить буклет-памятку со всеми изученными способами
решения квадратных уравнений
Гипотеза:
Любое квадратное уравнение можно решить всеми
существующими способами.

3. История развития квадратных уравнений Квадратные уравнения в Индии.

Задачи на квадратные уравнения встречаются уже в астрономическом
тракте «Ариабхаттиам», составленном в 499 г. индийским
математиком и астрономом Ариабхаттой.
Другой индийский ученный, Брахмагупта (VII в.), изложил общее
правило решения квадратных уравнений, приведенных к единой
канонической форме:
ах2 + bх = с, а > 0.
(1)
В уравнении (1) коэфиценты, кроме а, могут быть и отрицательными.
Правило Брахмагупты по существу совпадает с нашим.

4.

Вот одна из задач знаменитого индийского математика XII в.
Бхаскары.
Задача 13.
«Обезьянок резвых стая
А двенадцать по лианам…
Власть поевши, развлекалась.
Стали прыгать, повисая…
Их в квадрате часть восьмая
Сколько ж было обезьянок,
На поляне забавлялась.
Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных
уравнений (рис. 3).
Соответствующее задаче 13 уравнение:
(x/8)2 + 12 = x
Бхаскара пишет под видом:
х2 - 64х = -768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям
322, получая затем:
х2 - 64х + 322 = -768 + 1024,
(х - 32)2 = 256,
х - 32 = ± 16,
х1 = 16, х2 = 48.

5. Способ №1. Разложение на множители левой части уравнения

Решим уравнение х2 + 10х – 24 = 0.
Разложим на множители левую часть: х2 + 10х – 24 = х2
+ 12х – 2х – 24 = х(х + 12) – 2(х + 12) = (х + 12)(х – 2).
Уравнение примет вид:
(х + 12)(х – 2) = 0;
х + 12 = 0 или х – 2 = 0
х = -12.
х = 2.
Ответ: -12; 2.

6. Способ №2. Метод выделения полного квадрата (1 случай)

Решим уравнение х2 – 10х + 25 = 0.
Заметим, что левая часть уравнения представляет собой
полный квадрат двучлена.
Запишем уравнение в виде: (х – 5)2 = 0;
х – 5 = 0;
х = 5.
Ответ: 5.

7. Метод выделения полного квадрата (2 случай)

Решим уравнение х2 + 6х – 7 = 0.
Выделим квадрат двучлена в левой части уравнения.
х2 + 6х – 7 = х2 + 6х + 32 – 32 – 7 = (х + 3)2 – 9 – 7 = (х + 3)2
– 16.
Уравнение примет вид: (х + 3)2 – 16 = 0;
(х + 3)2 = 16;
х + 3 = 4 или х + 3 = - 4
х = 1.
х = -7.
Ответ: -7 ; 1.

8. Способ №3. Решение квадратных уравнений по формуле

aх2 + bx + c = 0
D = b2 – 4ac
D<0
Корней нет
D=0
D>0

9. Решение квадратных уравнений по формуле

Решим уравнение х2 - 4x - 5 = 0
D = b2 - 4ac = (-4)2 - 4 * 1 * (-5) = 16 + 20 = 36
х1 = (4 + 6) : 2 = 5,
х2 = (4 - 6) : 2 = -1
Ответ: - 1; 5

10. Способ №4. Решение уравнений с использованием теоремы Виета

Как известно, приведенное квадратное уравнение
имеет вид
х2 + px + c = 0
Его корни удовлетворяют теореме Виета, которая при a=1
имеет вид
х1 х2 = q,
х1 +х2 = -p

11. Решение уравнений с использованием теоремы Виета

Решим уравнение х2 +10х – 24 = 0.
а = 1, это приведённое квадратное уравнение.
Заметим, что D>0 и х1 х2 = - 24,
х1 +х2 = -10, значит
х1 = - 12, х2 = 2.
Ответ: - 12; 2.

12. Способ №5. Решение уравнений способом переброски

Дано уравнение ах2 + bх + с = 0.
Умножим обе части уравнения на а, получим а2 х2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а. Тогда у2 + bу + ас = 0.
Его корни у1 и у2 . Окончательно х1 = у1 /а, х1 = у2 /а.
Решим уравнение 2х2 - 11х + 15 = 0.
Перебросим коэффициент 2 к свободному члену:
у2 - 11у + 30= 0.
Согласно теореме, обратной теореме Виета у1 = 5 и у2 = 6.
Значит х1 = 5/2 и х2 = 6/2 или х1 = 2,5 и х2 = 3.
Ответ: 2,5; 3.

13. Способ №6. Свойства коэффициентов квадратного уравнения (1 случай)

Если a + b + c = 0, то х1 = 1, х2 = с/a.
Решим уравнение х2 + 6х – 7 = 0, где а = 1, b = 6, с = - 7.
Заметим, что D>0 и 1 + 6 – 7 = 0, значит
х1 = 1, х2 = - 7/1 = - 7.
Ответ: - 7; 1.

14. Свойства коэффициентов квадратного уравнения (2 случай)

Если a – b + c = 0, то х1 = - 1, х2 = -с/а.
Решим уравнение 3х2 +5х +2 = 0, где а = 3, b = 5, с = 2.
Заметим, что D>0 и 3 - 5 + 2 = 0, значит
х1= - 1, х2 = - 2/3.
Ответ: - 1; - 2/3.

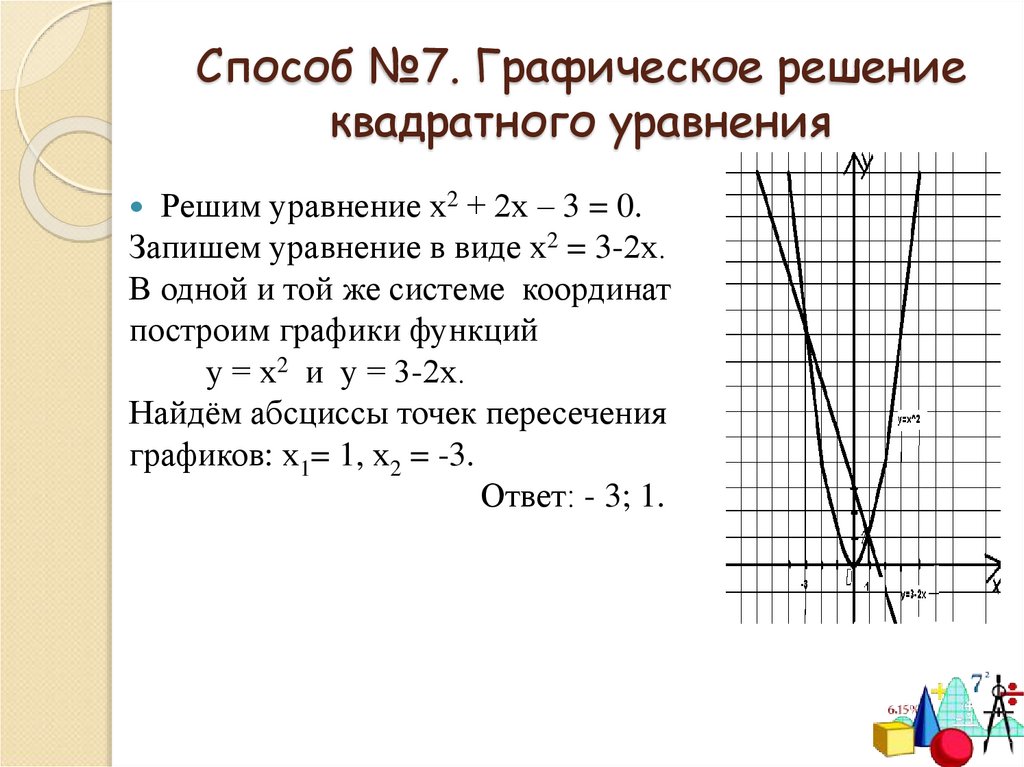
15. Способ №7. Графическое решение квадратного уравнения

Решим уравнение х2 + 2х – 3 = 0.
Запишем уравнение в виде х2 = 3-2х.
В одной и той же системе координат
построим графики функций
у = х2 и у = 3-2х.
Найдём абсциссы точек пересечения
графиков: х1= 1, х2 = -3.
Ответ: - 3; 1.

16. Заключение

В ходе данной работы мною были изучены способы решения
полных квадратных уравнений
Квадратные уравнения находят широкое применение при решении
тригонометрических, показательных, логарифмических,
иррациональных и трансцендентных уравнений и неравенств.
Квадратные уравнения играют огромную роль в развитии
математики. Все мы будем решать квадратные уравнения со
школьной скамьи, до окончания вуза. Эти знания могут
пригодиться нам на протяжении всей жизни.
Так как эти методы решения квадратных уравнений просты в
применении, то они, безусловно, должны заинтересовать
увлекающихся математикой учеников. Моя работа дает
возможность по-другому посмотреть на те задачи, которые ставит
перед нами математика. Считаю, что работа помогла мне лучше
подготовиться к ОГЭ по математике.
Пока я работал над этой темой я научился решать уравнения
различными спобами и научил некоторых своих одноклассников
Я провел опрос о наипростейшим способе решения уравнений

17.

Я работал под девизом: «Научился сам – научи
другого!».

18. Литература

1.
Алимов Ш.А., Ильин В.А. и др. Алгебра 6-8. Пробный учебник для 6-8 классов
средней школы.- М., Просвещение, 1981.
2.
Брадис В.М. Четырехзначные математические таблицы для средней школы. Изд.
57-е.-М., Просвещение, 1990. С. 83.
3.
Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям.
Учебное пособие для средних специальных учебных заведений. -М., высшая
школа, 1969.
4.
Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для
учителя. –М., Просвещение, 1972.
5.
Пресман А.А. Решение квадратного уравнения с помощью циркуля и ленейки. –
М., Квант, №4/72.С. 34.
6.
Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. -4-е
дополн. –М., Высшая школа,1973.
7.
Худобин А.И. Сборник задач по алгебре и элементарным функциям . Пособие
для учителя. Изд. 2-е. –М., Просвещение, 1970.