Анализ сложности алгоритмов

1.

1

2.

2

3.

Важные факторы точного анализа обычно находятся за пределами области
действия программиста:
• программы C++ переводятся в машинные коды для данного типа
компьютера, и может оказаться достаточно сложной задачей
определить, сколько времени займет выполнение даже одного
оператора C++ (особенно в среде, где возможен совместный доступ к
ресурсам так, что одна и та же программа может иметь различные
характеристики производительности в разное время)
• многие программы чрезвычайно чувствительны ко входным данным,
поэтому производительность может меняться в больших пределах в
зависимости от них
• многие интересующие нас программы еще не поняты до конца, поэтому
для них пока не существует специальных математических результатов
• две программы могут совершенно не поддаваться сравнению: одна
работает эффективно с определенным типом входных данных, другая
выполняется эффективно при других обстоятельствах
3

4.

Первый шаг при анализе алгоритма состоит в определении
абстрактных операций, на которых основан алгоритм, чтобы
отделить анализ от реализации.
Отделяем изучение того, сколько раз одна из реализаций алгоритма
запускает фрагмент кода i=a[i], от подсчета, сколько наносекунд
требуется для выполнения этого фрагмента кода на данном
компьютере.
Для определения реального времени выполнения программы на
заданном типе компьютера требуются оба упомянутых элемента.
Первый из них определяется свойствами алгоритма, последний —
свойствами компьютера.
Такое разделение позволяет сравнивать алгоритмы таким способом,
который не зависит от определенной реализации или от
определенного типа компьютера.
Хотя количество используемых абстрактных операций может оказаться
очень большим, производительность алгоритма обычно зависит
от нескольких величин, причем наиболее важные для анализа
величины, как правило, определить несложно.
4

5.

Один из способов определения величин для анализа
заключается в использовании механизма
профилирования
(механизма, доступного во многих реализациях C++, который включает
в себя счетчик количества выполнений каждой инструкции)
для нахождения наиболее часто исполняемых частей
программы по результатам нескольких пробных
запусков.
В любом случае, анализ сводится к определению
частоты исполнения нескольких фундаментальных
операций.
Необходимо отыскать приблизительные оценки этих
величин.
5

6.

Часто время выполнения программы зависит от размера
исходных данных
Большинство алгоритмов имеют главный параметр N,
который значительно влияет на время их выполнения
Параметр N:
– степень полинома
– размер файла при сортировке или поиске
– количество символов в строке …
Чаще всего, параметр N прямо пропорционален
величине обрабатываемого набора данных
6

7.

Асимптотическая оценка
Вычисление времени выполнения программ
Асимптотическая оценка временной и/или
пространственной сложности используется для того,
чтобы выделить существенные свойства алгоритма или
программы.
Цель - выражение ресурсных требований программ (как
правило, времени выполнения) в зависимости от N с
использованием математических формул, которые
максимально просты и справедливы для больших
значений параметров.
Для описания временной сложности алгоритмов
используется О-символика.
7

8.

Например,
если время выполнения Т(N) некоторой программы имеет порядок O(N2)
(читается «O -большое от N в квадрате» или просто «O от N в квадрате»),
это означает,
что существуют положительные константы
с и N0 такие,
что для всех N, больших или равных N0,
выполняется неравенство T(N) c*N 2.
Запись O(fc(N)) для временной сложности T(N) означает,
что с > 0, N0 > 0 такие, что для всех N N0,
выполняется неравенство fc(N) T(N).
Т(N) имеет порядок О ( f(N) )
Для программ, у которых время выполнения имеет порядок О(f(N)), говорят,
что они имеют порядок (или степень) роста f(N).
8

9.

Например:
фраза «сложность алгоритма есть O(n!)» означает,
что с увеличением параметра n, характеризующего количество
входной информации алгоритма, время работы алгоритма
растёт не быстрее, чем (пропорционально) n!;
Чтобы записать время работы алгоритма в О-обозначениях,
достаточно изучить общую структуру алгоритма.
Например, наличие двойного вложенного цикла в структуре
алгоритма сортировки по методу вставок, свидетельствует о
том, что верхний предел времени работы в наихудшем случае
выражается как :
"стоимость" каждой итерации во внутреннем цикле ограничена
сверху константой O(1),
индексы i и j — числом n,
а внутренний цикл выполняется самое большее один раз для
каждой из пар значений i и j.
9

10.

10

11.

Пример 1:
Время выполнения T(n)=(n+1)2
T(0)=1, T(1)=4
Пусть n0=1, c=4.
Тогда T(n) имеет порядок O(n2), т.к. для n 1 будет
выполняться неравенство (n+1)2 4n2.
Пример 2:
Время выполнения T(n)=3n3+2n2.
T(0)=0, T(1)=5.
Положим n0=0, c=5.
Тогда T(n) имеет порядок O(n3), т.к. для n 0 будет
выполняться неравенство 3n3 + 2n2 5n3.
11

12.

Вычисление времени выполнения программ
Теоретическое нахождение времени выполнения программ (даже без
определения констант пропорциональности) — сложная математическая
задача.
На практике определение времени выполнения (также без нахождения значения
констант) является вполне разрешимой задачей — для этого нужно знать
только несколько базовых принципов.
Рассмотрим, как выполняются операции сложения и умножения с использованием
О-символики.
Пусть T1(n) и Т2(n) — время выполнения двух программных фрагментов Р1 и Р2,
T1(n) имеет степень роста O(f(n)), а Т2(n) — O(g(n)).
Тогда T1(n) + Т2(n), т.е. время последовательного выполнения фрагментов Р1 и Р2,
имеет степень роста O(max(f(n), g(n))).
Правило сумм: порядок временной сложности суммы функций равен порядку
максимального из слагаемых: O(N5+N2+N)=O(N5)
В общем случае время выполнения конечной последовательности программных
фрагментов, без учета констант, имеет порядок фрагмента с наибольшим
временем выполнения .
12

13.

Правило произведений
Если T1(n) и Т2(n) имеют степени роста O(f(n)) и O(g(n)) соответственно, то
произведение T1(n) Т2(n)имеет степень роста O(f(n)g(n)).
порядок временной сложности произведения двух функций равен
произведению их сложностей
Из правила произведений следует, что O(c*f(n)) эквивалентно O(f(n)),
если с — положительная константа.
Например, О(n2/2) эквивалентно О(n2).
постоянные множители не имеют значения для определения порядка
временной сложности, т.е. O(k*f)=O(f))
Пусть две программы P1 и P2 имеют асимптотическую сложность
О( f(N) ) и О( g(N) ) соответственно,
тогда асимптотическая сложность T1(N)*T2(N) будет О(f(N)*g(N)).
13

14.

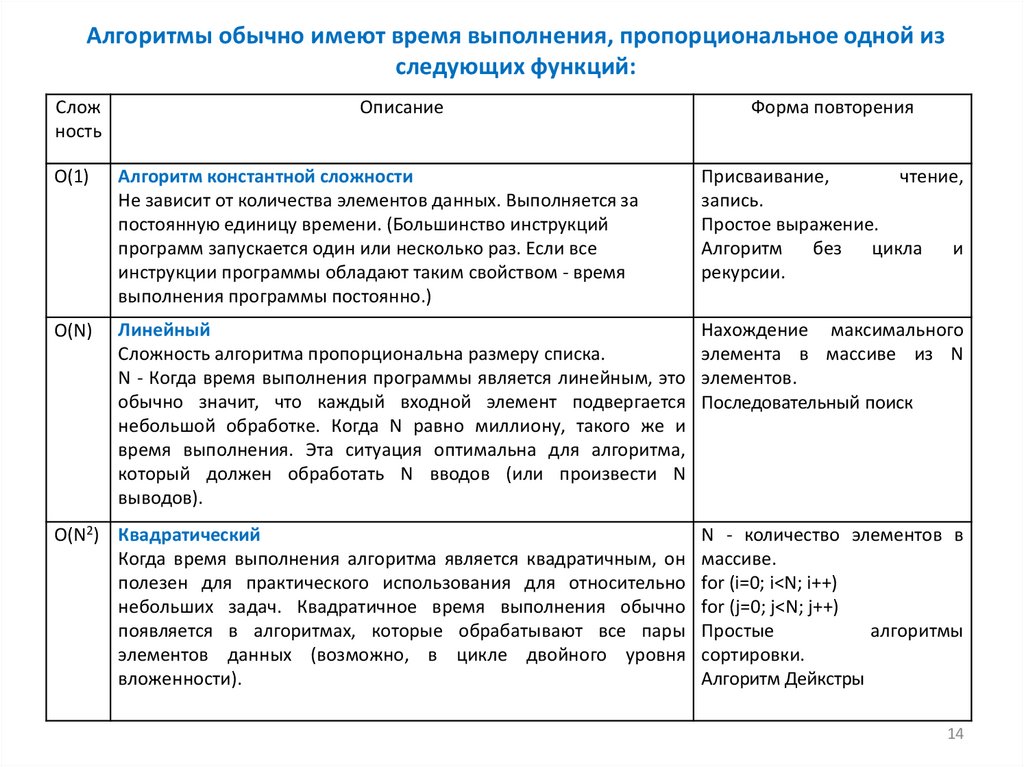
Алгоритмы обычно имеют время выполнения, пропорциональное одной из
следующих функций:
Слож
ность
Описание
Форма повторения
O(1)
Алгоритм константной сложности
Не зависит от количества элементов данных. Выполняется за
постоянную единицу времени. (Большинство инструкций
программ запускается один или несколько раз. Если все
инструкции программы обладают таким свойством - время
выполнения программы постоянно.)
Присваивание,
чтение,
запись.
Простое выражение.
Алгоритм без цикла и
рекурсии.
O(N)
Линейный
Сложность алгоритма пропорциональна размеру списка.
N - Когда время выполнения программы является линейным, это
обычно значит, что каждый входной элемент подвергается
небольшой обработке. Когда N равно миллиону, такого же и
время выполнения. Эта ситуация оптимальна для алгоритма,
который должен обработать N вводов (или произвести N
выводов).
Нахождение максимального
элемента в массиве из N
элементов.
Последовательный поиск
O(N2) Квадратический
Когда время выполнения алгоритма является квадратичным, он
полезен для практического использования для относительно
небольших задач. Квадратичное время выполнения обычно
появляется в алгоритмах, которые обрабатывают все пары
элементов данных (возможно, в цикле двойного уровня
вложенности).
N - количество элементов в
массиве.
for (i=0; i<N; i++)
for (j=0; j<N; j++)
Простые
алгоритмы
сортировки.
Алгоритм Дейкстры
14

15.

Сложность
Описание
Форма повторения
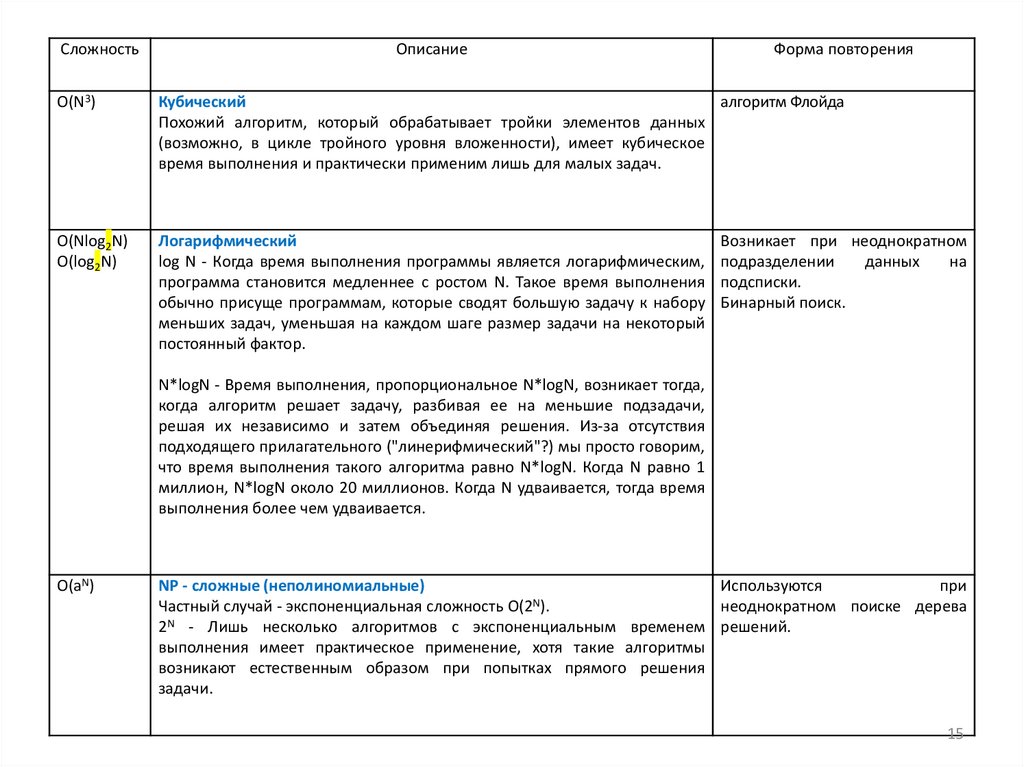
O(N3)
Кубический
алгоритм Флойда
Похожий алгоритм, который обрабатывает тройки элементов данных
(возможно, в цикле тройного уровня вложенности), имеет кубическое
время выполнения и практически применим лишь для малых задач.
O(Nlog2N)
O(log2N)
Логарифмический
log N - Когда время выполнения программы является логарифмическим,
программа становится медленнее с ростом N. Такое время выполнения
обычно присуще программам, которые сводят большую задачу к набору
меньших задач, уменьшая на каждом шаге размер задачи на некоторый
постоянный фактор.
Возникает при неоднократном
подразделении
данных
на
подсписки.
Бинарный поиск.
N*logN - Время выполнения, пропорциональное N*logN, возникает тогда,
когда алгоритм решает задачу, разбивая ее на меньшие подзадачи,
решая их независимо и затем объединяя решения. Из-за отсутствия
подходящего прилагательного ("линерифмический"?) мы просто говорим,
что время выполнения такого алгоритма равно N*logN. Когда N равно 1
миллион, N*logN около 20 миллионов. Когда N удваивается, тогда время
выполнения более чем удваивается.
O(aN)
NP - сложные (неполиномиальные)
Используются
при
N
Частный случай - экспоненциальная сложность O(2 ).
неоднократном поиске дерева
N
2 - Лишь несколько алгоритмов с экспоненциальным временем решений.
выполнения имеет практическое применение, хотя такие алгоритмы
возникают естественным образом при попытках прямого решения
задачи.
15

16.

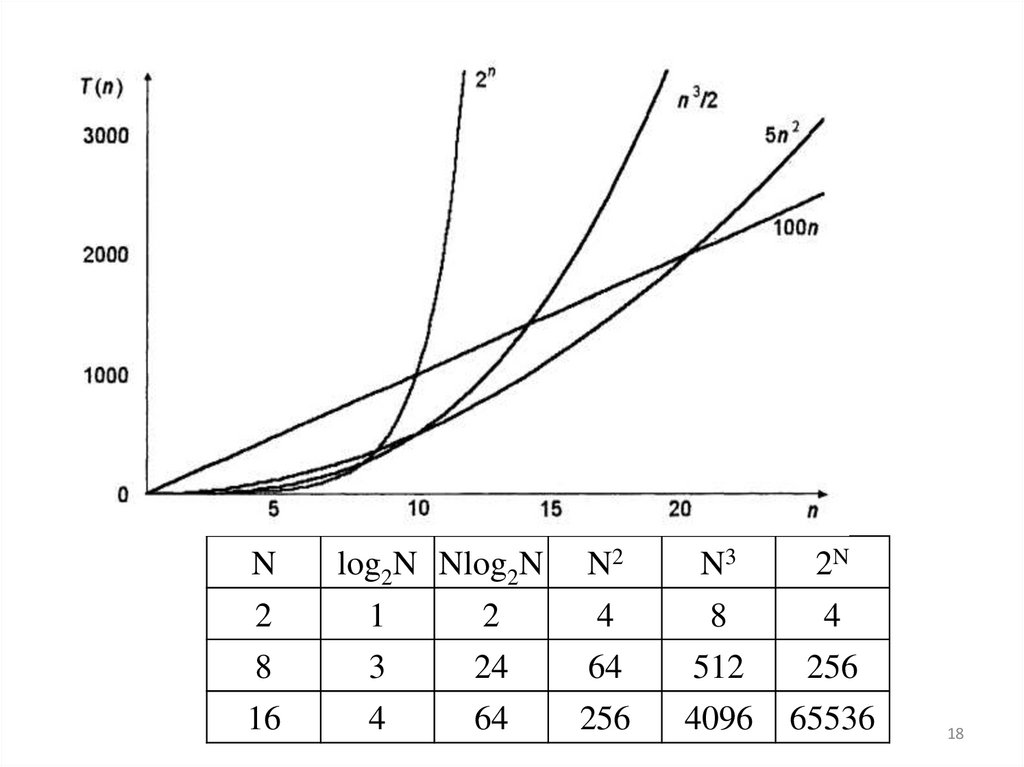
Значения часто встречающихся функций
В таблице показаны относительные величины некоторых функций, которые
часто встречаются при анализе алгоритмов.
Очевидно, доминирующей является квадратичная функция, особенно для
больших значений N, а значения между меньшими функциями оказываются
не такими, как можно было ожидать для малых N.
Например, N 3/2 больше, чем N*lg2N для огромных значений N, однако для
небольших N наблюдается обратная ситуация.
16

17.

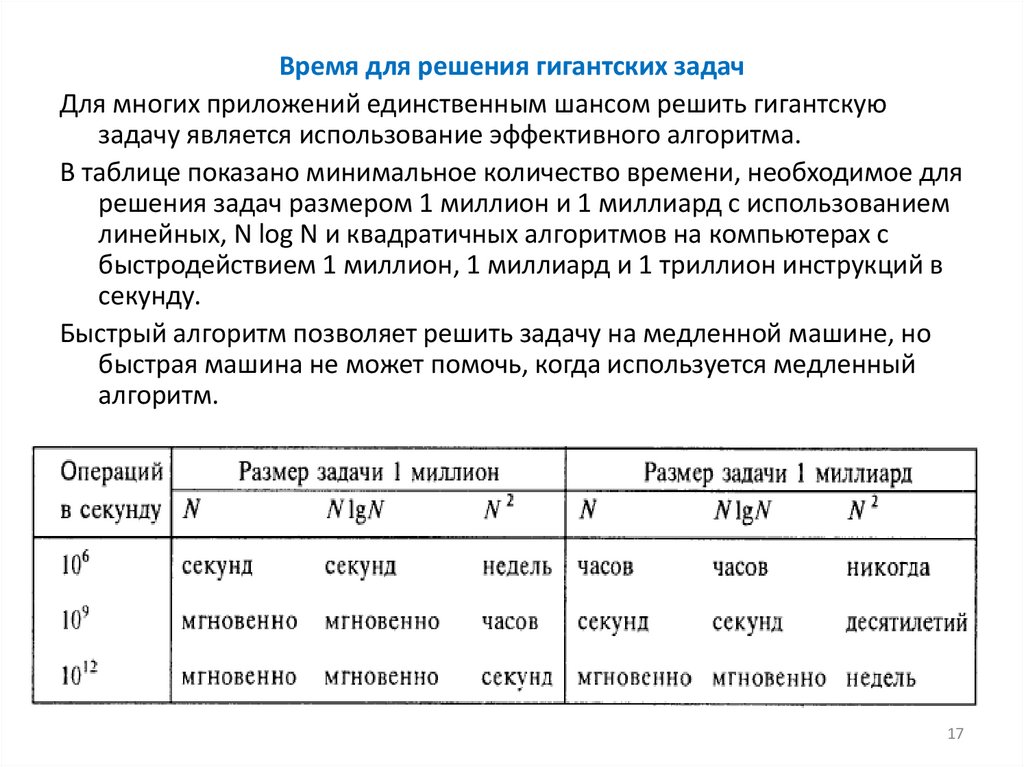
Время для решения гигантских задач
Для многих приложений единственным шансом решить гигантскую
задачу является использование эффективного алгоритма.
В таблице показано минимальное количество времени, необходимое для
решения задач размером 1 миллион и 1 миллиард с использованием
линейных, N log N и квадратичных алгоритмов на компьютерах с
быстродействием 1 миллион, 1 миллиард и 1 триллион инструкций в
секунду.
Быстрый алгоритм позволяет решить задачу на медленной машине, но
быстрая машина не может помочь, когда используется медленный
алгоритм.
17

18.

N
log2N Nlog2N
N2
N3
2N
2
1
2
4
8
4
8
3
24
64
512
256
16
4
64
256
4096
65536
18

19.

Предположим, что можно использовать 1000 секунд (примерно 17
минут) машинного времени для решения задачи.
Какой максимальный размер задачи, решаемой за это время?
За 103 секунд каждый из четырех алгоритмов может решить задачи
примерно одинакового размера, как показано во втором столбце
таблицы.
Предположим, что получен новый компьютер, работающий в десять раз
быстрее.
Таблица. Эффект от 10-кратного увеличения быстродействия компьютера
19

20.

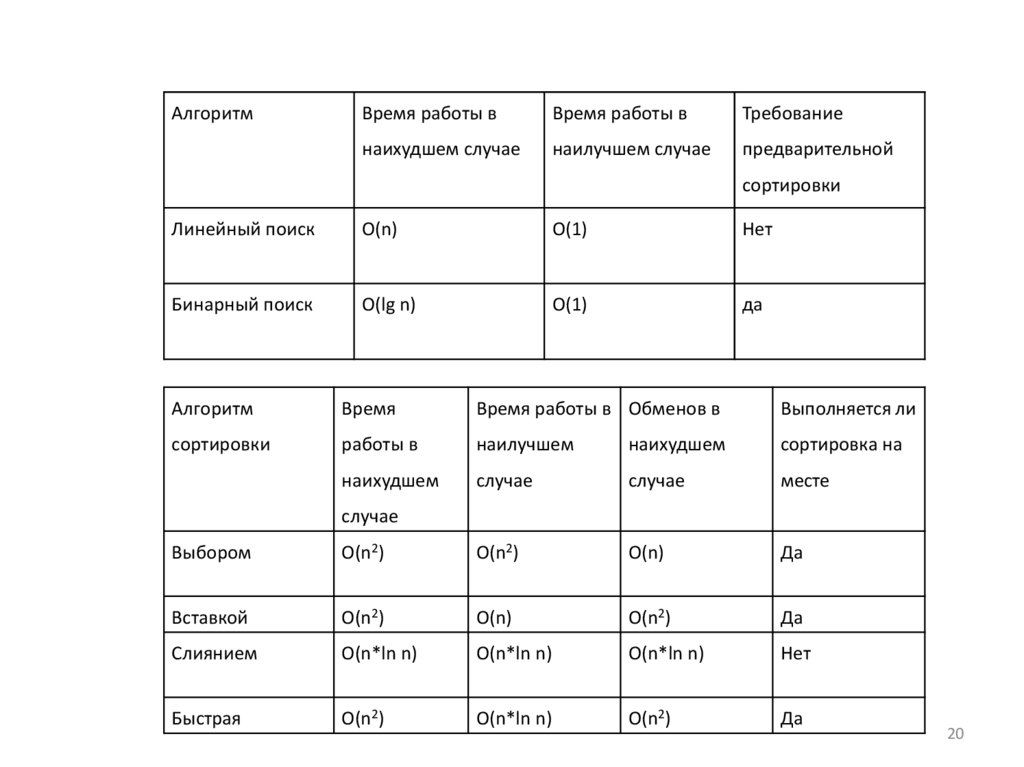
Алгоритм
Время работы в
Время работы в
Требование
наихудшем случае
наилучшем случае
предварительной
сортировки
Линейный поиск
О(n)
O(1)
Нет
Бинарный поиск
O(lg n)
O(1)
да
Алгоритм
Время
Время работы в Обменов в
Выполняется ли
сортировки
работы в
наилучшем
наихудшем
сортировка на
наихудшем
случае
случае
месте
случае
Выбором
O(n2)
O(n2)
O(n)
Да
Вставкой
O(n2)
O(n)
O(n2)
Да
Слиянием
O(n*ln n)
O(n*ln n)
O(n*ln n)
Нет
Быстрая
O(n2)
O(n*ln n)
O(n2)
Да
20