Похожие презентации:
Застосування методу комплексних амплітуд
1.
ЛЕКЦІЯ 3.3ЗАСТОСУВАННЯ МЕТОДУ
КОМПЛЕКСНИХ АМПЛІТУД
2.
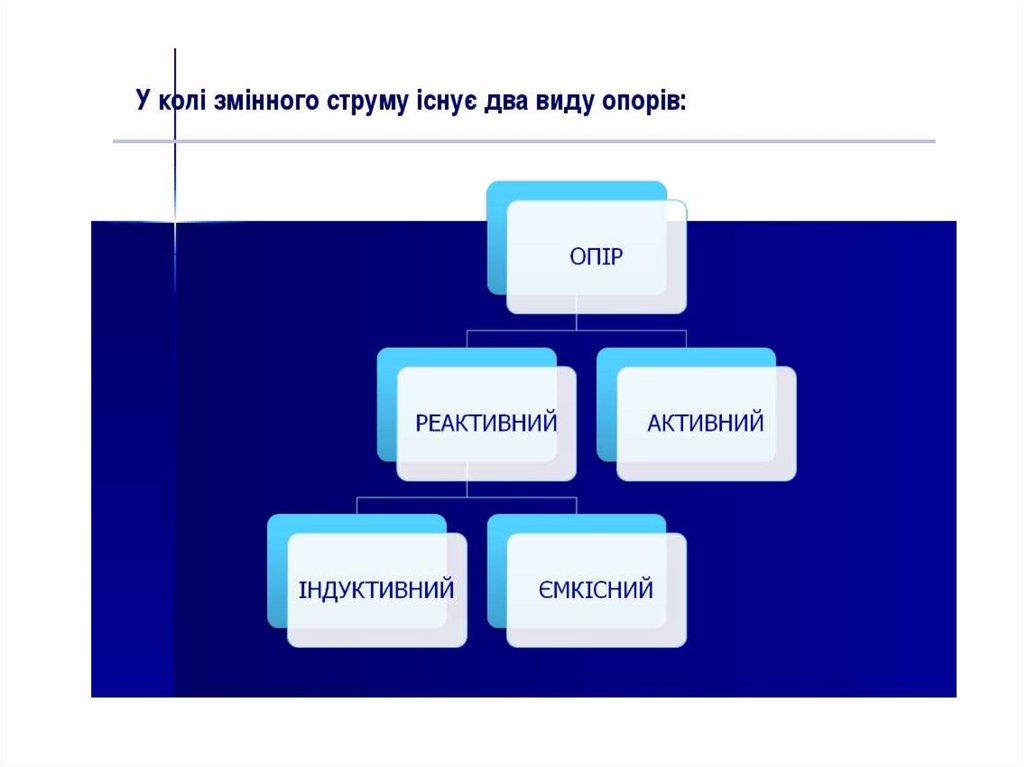
План лекції:• Поняття про комплексний опір
та комплексну провідність.
• Компонентні рівняння пасивних
двополюсних компонентів в
комплексній формі та їх
комплексні схеми заміщення.
3.
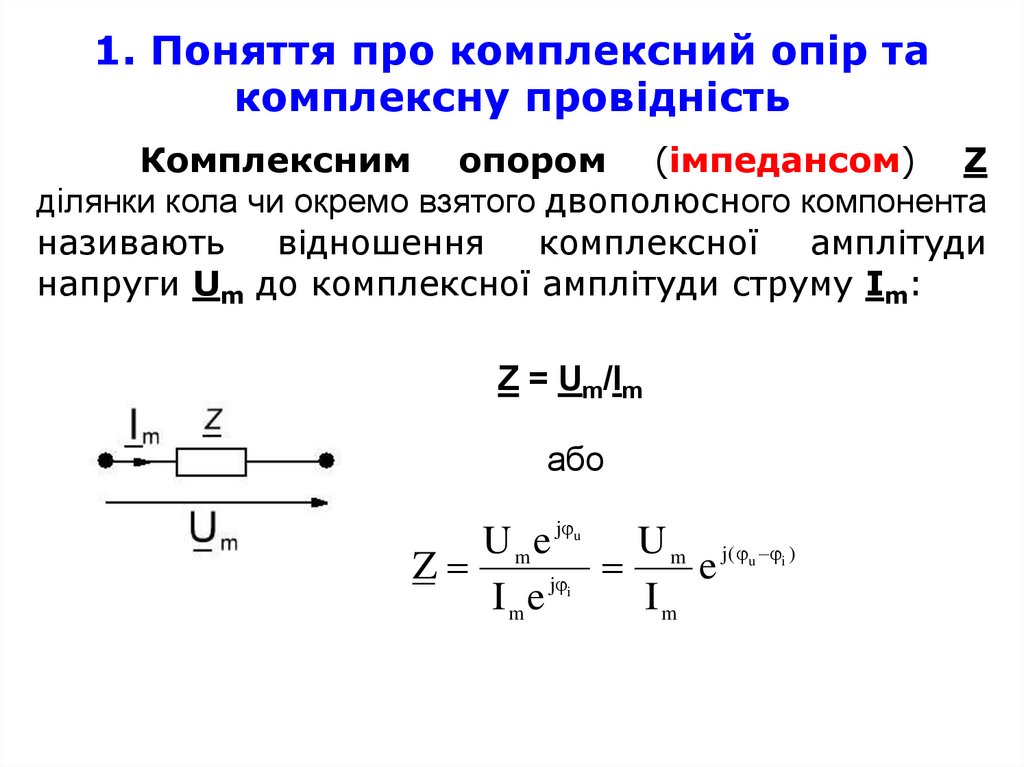
1. Поняття про комплексний опір такомплексну провідність
Комплексним опором (імпедансом) Z
ділянки кола чи окремо взятого двополюсного компонента
називають
відношення
комплексної
амплітуди
напруги Um до комплексної амплітуди струму Im:
Z = Um/Im
або
U m e j
U m j ( )
Z
e
j
Ime
Im
u
u
i
i
4.
Оскількита
є комплексними числами ,
то комплексний опір Z є теж комплексним
числом, яке можна записати в показниковій
або в алгебраїчній формі
Величини Z та Z
називають відповідно
модулем та аргументом комплексного опору,
а R та X – відповідно резистивною (дійсною)
та реактивною (уявною) складовою
комплексного опору Z.
5.
U m e jU m j ( )
Z
e
j
Ime
Im
u
u
i
i
Отже, модуль Z комплексного опору дорівнює
Z амплітуд напруги і струму на
відношенню
зовнішніх виводах двополюсника
а аргумент
дорівнює різниці початкових фаз
напруги і струму:
Z u i
Резистивна складова комплексного опору
U
(резистанс):
R Z cos z m cos( u i )
Im
Реактивна складова комплексного опору (реактанс):
Um
X Z sin z
sin( u i ).
Im
6.
Величиною, оберненою до комплексного опоруZ,
є
комплексна
провідність
Y=1/Z
(адмітанс),
яку
можна
записати
в
показниковій або в алгебраїчній формі, виразивши
j i
їх також через комплексні
амплітуди:
:
I me
I m j ( i u )
j y
Y
e
Ye ,
j u
U me
Um
Y
Im
cos( i u ) j sin( i u ) G jB.
Um
Iпровідності:
1
Модуль комплексної
m
Y
.
Um Z
Аргумент комплексної
провідності:
.
y
i
u
7.
Дійсна складова комплексної провідності (кондуктанс) :Im
G Y cos y
cos( i u );
Um
Уявна складова комплексної провідності (сусцептанс) :
Im
B Y sin y
sin( i u ).
Um
Взаємозв’язок між модулями і аргументами та дійсними
і уявними частинами комплексного опору та
комплексної провідності:
Z R 2 X 2 ; Z arc tg ( X / R );
Y G 2 B 2 ; y arc tg ( B / G );
R
X
;
B
; y Z ;
2
2
2
2
R X
R X
G
B
R 2
;
X
.
2
2
2
G B
G B
G
8.
2. Компонентні рівняння пасивних двополюснихкомпонентів в комплексній формі та їх комплексні
схеми заміщення
3.1. Лінійний резистор
Розглянемо лінійний резистор, який представимо ідеальним
резистивним елементом:
iR(t)
uR(t)
Приймемо, що через нього протікає гармонічний струм:
iR(t) = ImRcos( t+ i).
Враховуючи компонентне рівняння лінійного резистора,
визначимо напругу, яка прикладена до нього:
uR(t) = R iR(t) = RImRcos( t+ i).
9.
Бачимо, що амплітуда напруги дорівнює UmR = RImR, а їїпочаткова фаза u дорівнює початковій фазі струму i,
тобто струм і напруга резистора збігаються за фазою (є
синфазні):
u = i ,
uR(t)
iR(t)
10.
Комплексні амплітуди струму та напруги, відповідно,дорівнюють:
ImR I m e j i ;U mR RI mR e j i .
Комплексний опір лінійного резистора дорівнює:
U mR
j 00
ZR
Re R.
ImR
Отже, комплексний опір лінійного резистора є
величиною дійсною і дорівнює R, а його аргумент
дорівнює нулеві.
Комплексна схема заміщення
лінійного резистора:
Векторна діаграма:
11.
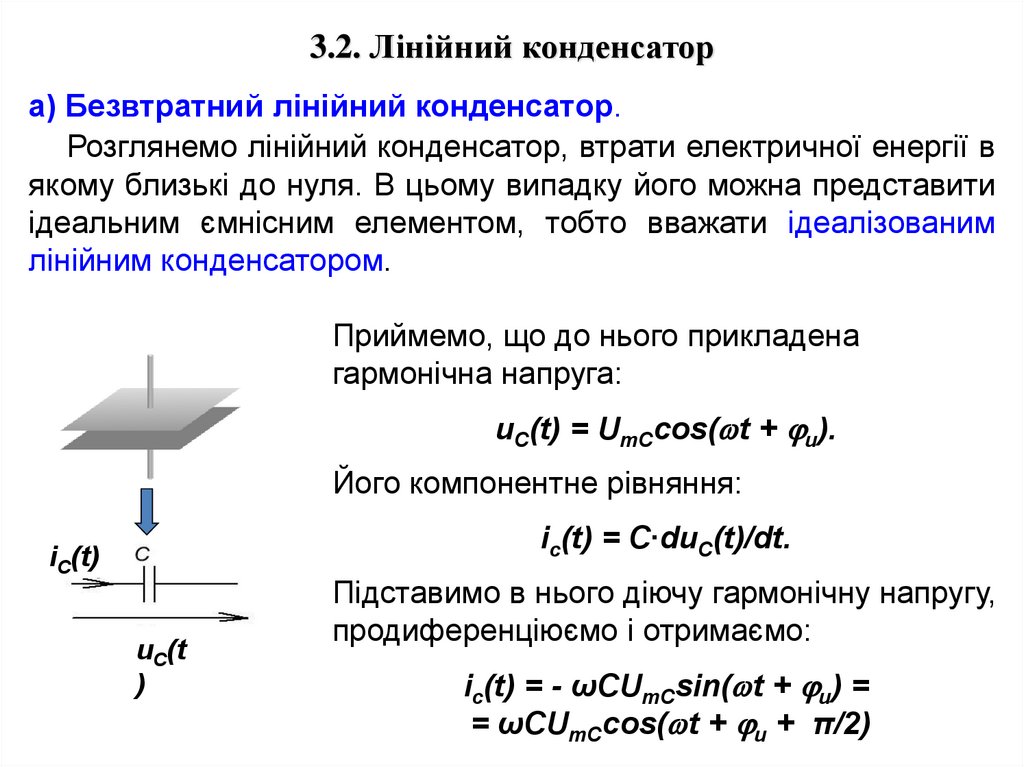
3.2. Лінійний конденсатора) Безвтратний лінійний конденсатор.
Розглянемо лінійний конденсатор, втрати електричної енергії в
якому близькі до нуля. В цьому випадку його можна представити
ідеальним ємнісним елементом, тобто вважати ідеалізованим
лінійним конденсатором.
Приймемо, що до нього прикладена
гармонічна напруга:
uС(t) = UmСcos( t + u).
Його компонентне рівняння:
ic(t) = C∙duC(t)/dt.
iC(t)
uC(t
)
Підставимо в нього діючу гармонічну напругу,
продиференціюємо і отримаємо:
ic(t) = - ωCUmCsin( t + u) =
= ωCUmCcos( t + u + π/2)
12.
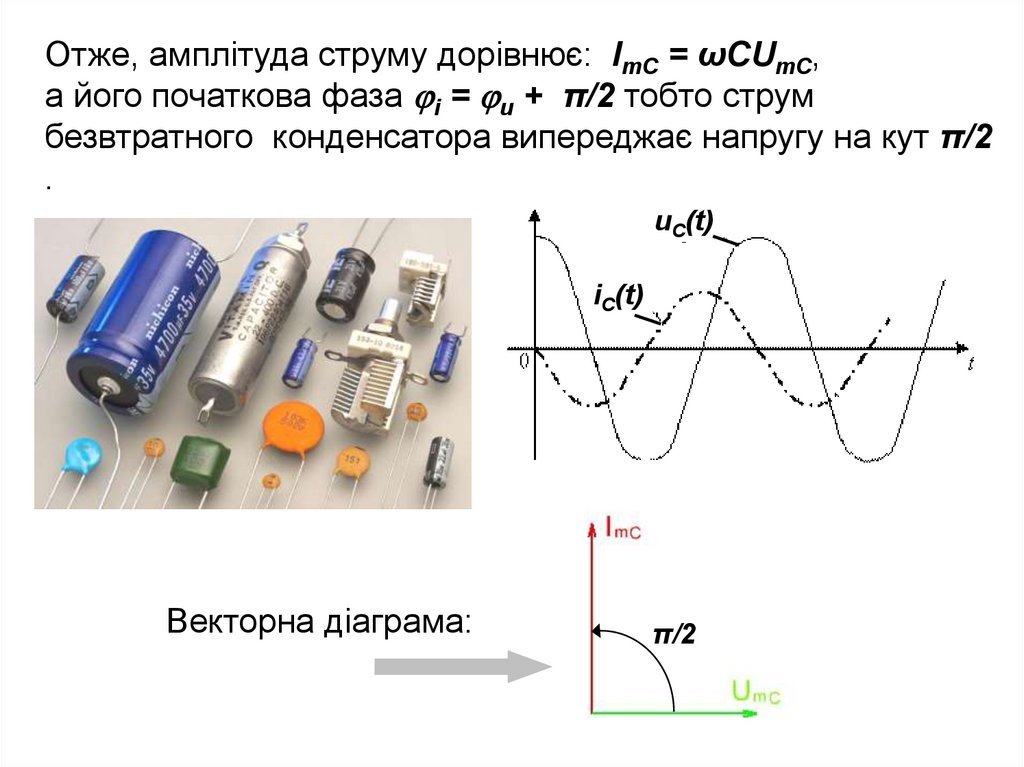
Отже, амплітуда струму дорівнює: ImC = ωCUmC,а його початкова фаза i = u + π/2 тобто струм
безвтратного конденсатора випереджає напругу на кут π/2
.
uC(t)
iC(t)
Векторна діаграма:
π/2
13.
Комплексні амплітуди напруги та струму безвтратногоконденсатора, відповідно, дорівнюють:
uС(t) = UmСcos( t + u)
UmC = UmCejφu
iС(t) = ImСcos( t + i) = ωCUmCcos( t + u + π/2)
ImC = ImCejφi = ωCUmCej( u+ π/2)
Комплексний опір безвтратного конденсатора дорівнює:
UmCejφu
1
1
1
-jπ/2
j
=
= jωC = ωC
ZC = UmC/ImC =
e
j(
+
π/2)
ωC
ωCUmCe u
Отже, комплексний опір безвтратного конденсатора є
величиною уявною. Такий опір називають реактивним.
14.
Дійсна (резистивна) складова комплексного опорубезвтратного конденсатора, як бачимо, дорівнює нулеві.
Модуль комплексного опору безвтратного конденсатора є
обернено пропорційний частоті:
1
Zc = X c =
.
ω
wC
Аргумент комплексного опору: φZ = -π/2.
φZ
|ZC|
0
-π/2
0
ω
ω
15.
Комплексна схема заміщення безвтратного лінійногоконденсатора:
ZC =
ω
1
jωC
16.
б) Втратний лінійний конденсатор.Реальні лінійні конденсатори характеризуються втратами
електричної енергії, пов‘язаними з неідеальністю діелектрика
та переполяризацією діелектрика при дії змінної напруги.
Тобто їх комплексний опір має як реактивну так і активну
складову:
ZC = RC + jXC = ZCejφ.zc
Кількісною характеристикою, яка свідчить про те,
наскільки
реальний
конденсатор
відрізняється
від
ідеального, є добротність QС, яку визначають як відношення
реактивної потужності конденсатора РQ до активної
потужності втрат РА:
QC =
PQ
PA
PQ =
PA =
Im2
2
Im2
2
X=
R=
Um2
2X
Um2
2R
17.
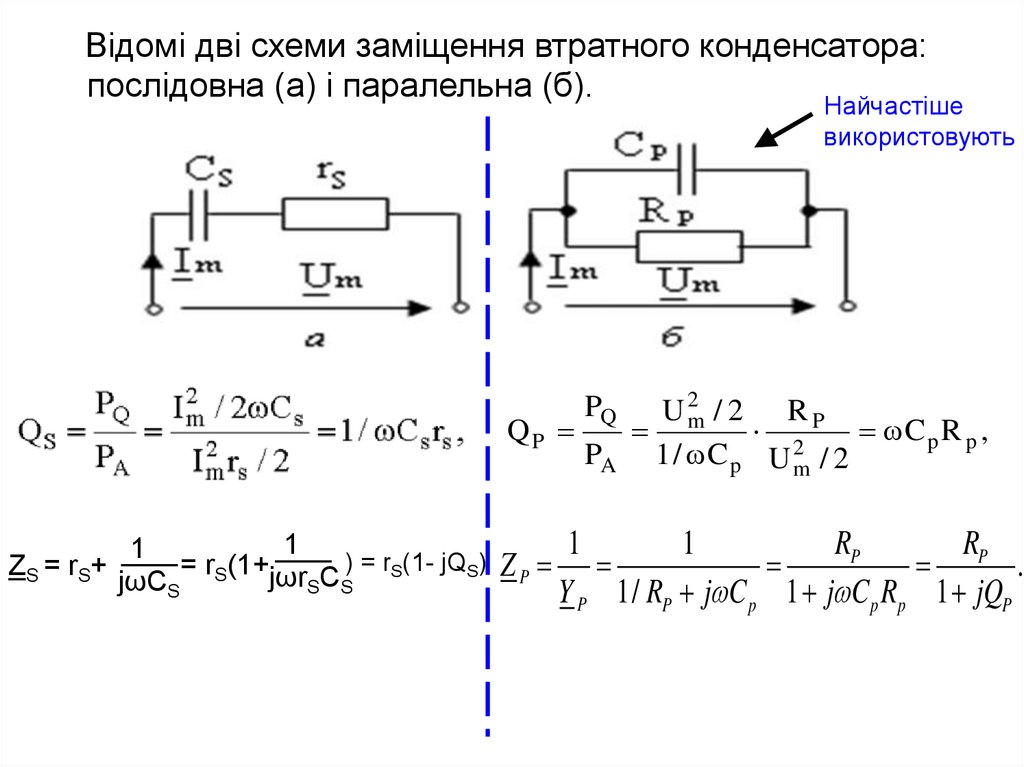
Відомi дві схеми заміщення втратного конденсатора:послідовна (а) і паралельна (б).
Найчастіше
використовують
U 2m / 2 R P
QP
2
C p R p ,
PA 1 / C p U m / 2
PQ
1
1
RP
RP
1
1
)
=
r
(1jQ
)
=
r
(1+
ZS = rS+
.
S ZP
jωCS S jωrSCS S
Y 1/ R j C 1 j C R 1 jQ
P
P
p
p p
P
18.
Схеми заміщення конденсатора є еквівалентні, отже:ZS = Zp = ZC
QS = Qp = QC
Прирівнявши наведені вище вирази для комплексних
опорів та добротностей реального конденсатора,
отримуємо співвідношення між параметрами обох схем
її заміщення:
2),
2)
r
=
R
/(1+1/Q
С
=
C
(1+1/Q
S
P
C
Найчастіше
S
P
C
використовують
де QC=ωRpCp
19.
Часто замість терміну «добротність» втратногоконденсатора використовують термін «тангенс кута втрат
δC », який є величиною, оберненою до добротності:
tg C 1 / QC = 1/(ωRpCp)
Фізичний зміст кута δC у тому, що він доповнює до
90o кут зсуву фаз між напругою і струмом втратного
конденсатора, тобто
C
20.
11
RP
RP
ZP
.
Y P 1/ RP j C p 1 j C p Rp 1 jQP
Модуль:
Zp = Rp/√ [1+(ωCpRp)2]
Аргумент:
φzp = - arc tg(ωCpRp)
Zp
φZp
Rp
0
ω
Зсув фази між напругою
i струмом з ростом частоти
прямує до –π/2
ω
-π/2
0
комп-
21.
3.3. Лінійна котушка індуктивностіа) Безвтратна лінійна котушка індуктивності.
Представимо її ідеальним індуктивним елементом, тобто
вважатимемо, що маємо ідеалізовану котушку індуктивності.
Приймемо, що через котушку протікає
гармонічний струм:
iL(t) = ImLcos( t + i).
Компонентне рівняння:
uL(t) = L∙diL(t)/dt.
iL(t)
Підставимо в нього гармонічний струм,
продиференціюємо і отримаємо:
uL(t)
uL(t) = - ωLImLsin( t + i) =
= ωLImLcos( t + i + π/2)
22.
Отже, амплітуда напруги безвтратної котушки дорівнює:UmL = ωLImL, а її початкова фаза u = i + π/2 тобто
напруга безвтратної котушки випереджає струм на кут π/2.
iL(t)
uL(t)
uL(t)
iL(t)
Векторна діаграма:
23.
Комплексні амплітуди струму та напруги безвтратноїкотушки, відповідно, дорівнюють:
iL(t) = ImLcos( t + i)
ImL = ImLejφ i
uL(t) = UmLcos( t + u) = ωLImLcos( t + i + π/2)
UmL = UmLejφu = ωLImLej( i + π/2)
Комплексний опір безвтратної котушки дорівнює:
ωLImLej( i + π/2)
= ωLejπ/2 = jωL
ZL = UmL/ImL =
jφ
ImLe i
Отже, комплексний опір безвтратної котушки є
величиною уявною. Такий опір, як вже було
зауважено, називають реактивним.
24.
Дійсна (резистивна) складова комплексного опорубезвтратної лінійної котушки індуктивності, як бачимо,
дорівнює нулеві.
Модуль комплексного опору безвтратної котушки є прямо
пропорційний частоті:
Z L X L L.
Аргумент комплексного опору: φZ = π/2.
φZ
|ZL|
π/2
0
ω
0
ω
25.
Комплексна схема заміщення безвтратної котушкиіндуктивності:
ZL = jωL
26.
б) Втратна лінійна котушка індуктивності.Реальні лінійні котушки індуктивності характеризуються
втратами електричної енергії, які мають місце в провіднику,
яким намотана котушка, а також у феромагнітному осерді в
звязку з його переполяризацією при дії змінного струму.
Тобто її комплексний опір має як реактивну так і активну
складову: ZL = RL + jXL = ZLejφ zL
Кількісною характеристикою, яка свідчить про те,
наскільки реальна котушка індуктивності відрізняється від
ідеальної, є добротність QL, яку визначають як відношення
реактивної потужності котушки РQ до активної потужності
втрат РА:
Im2
Um2
X=
PQ =
PQ
2
2X
QC =
PA
Im2
Um2
R=
PA =
2
2R
27.
Відомi дві схеми заміщення втратної котушкиіндуктивності: послідовна (а) і паралельна (б).
Найчастіше
використовують
ωLsIm2/2
rsIm
2/2
ωLs/rS
U 2m / 2 R P
QP
2
RCp/ωL
p R pp,
PA 1 /ωL
Cpp U m / 2
PQ
jωL1pRp
1
RP
RP
1
1
=
Z
=
r
+
jωL
=
r
(1
jQ
)
)
=
r
(1jQ
)
ZP
.
=
ZS = SrS+ S = rSs(1+jωr
S C
S
S
jωCS
S S
Y 1/ R j C 11-jR
j C/ωL
R 11-jQ
jQ
P
RpP+ jωLpp
p p
pp
pP
28.
Схеми заміщення котушки є еквівалентні, отже:ZS = Zp = ZL
QS = Qp = QL
Прирівнявши наведені вище вирази для комплексних
опорів та добротностей втратної котушки, отримуємо
співвідношення між параметрами обох схем її
заміщення:
LP LS (1
Найчастіше
Використовують:
1
),
2
Q L
R P rs (1 Q 2L )
де QL=ωLS /rS
Оскільки QL ˃˃ 1, то можемо прийняти:
LP LS ;
RP rS QL2 .
29.
ZS = rS+ jωLsМодуль:
ZS = rS√ [1+(ωLS/rS)2]
Аргумент:
φzS = arc tg(ωLS /rS)
Зсув фази між напругою
i струмом з ростом частоти
прямує до +π/2
arg
φZSZS
Z
ZS
S
/2
π/2
rS rS
0
ω
0
ω
Частотні характеристики модуля (а) та аргументу (б) комплексного
опору послідовної схеми заміщення котушки ындуктивносты
30.
31.
Отже, комплексні опори та комплексні провідностіідеалізованих пасивних двополюсних компонентів є такими:
iR(t)
ZR = R;
YR = 1/R.
uR(t)
iC(t)
ZC = 1/jωC;
YC = jωC.
ZL = jωL;
YL = 1/jωC.
uC(t
)
iL(t)
uL(t)
32.
Комплексні опори та комплексні провідностівтратних пасивних двополюсних компонентів є такими:
С
ZC = Rc/(1+jωRCC);
YC = 1/RC+ jωC.
RC
RL
L
ZL = RL+ jωL;
YL = 1/(RL+jωL).
33.
Приклади запису комплексних опорів та комплекснихпровідностей простих електричних ланок:
R
C
Z = R + 1/jωC
Y = 1/(R + 1/jωC)
R
Y = 1/R + jωC
Z = 1/(1/R + jωC) = R/(1+jωRC)
С
R
L
Z = R + jωL
Y = 1/(R + jωL)
Y = 1/R + 1/jωL
Z = jωL∙R/(R + jωL)
L
R





























 Физика
Физика








