Формы комплексного числа

1.

Выражение
z x i y
называется алгебраической формой
комплексного числа.
1

2.

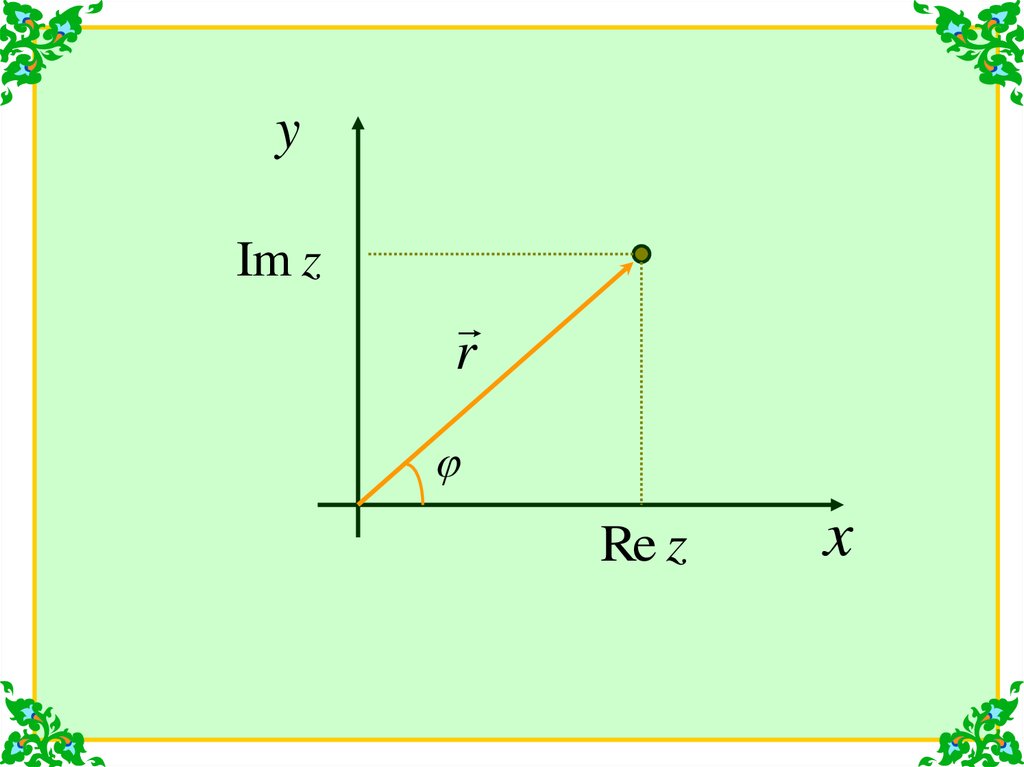
С каждой точкой комплексной плоскости
связан радиус-вектор точки OZ r
Длина этого вектора называется модулем
z
комплексного числа z и обозначается
r z
x y
2
2
Угол, образованный радиус-вектором точки и
осью х называется аргументом комплексного
числа z и обозначается Arg z
Из всех значений аргумента выделяется
главное значение arg z
удовлетворяющее условию arg z

3.

y
Im z
r
Re z
x

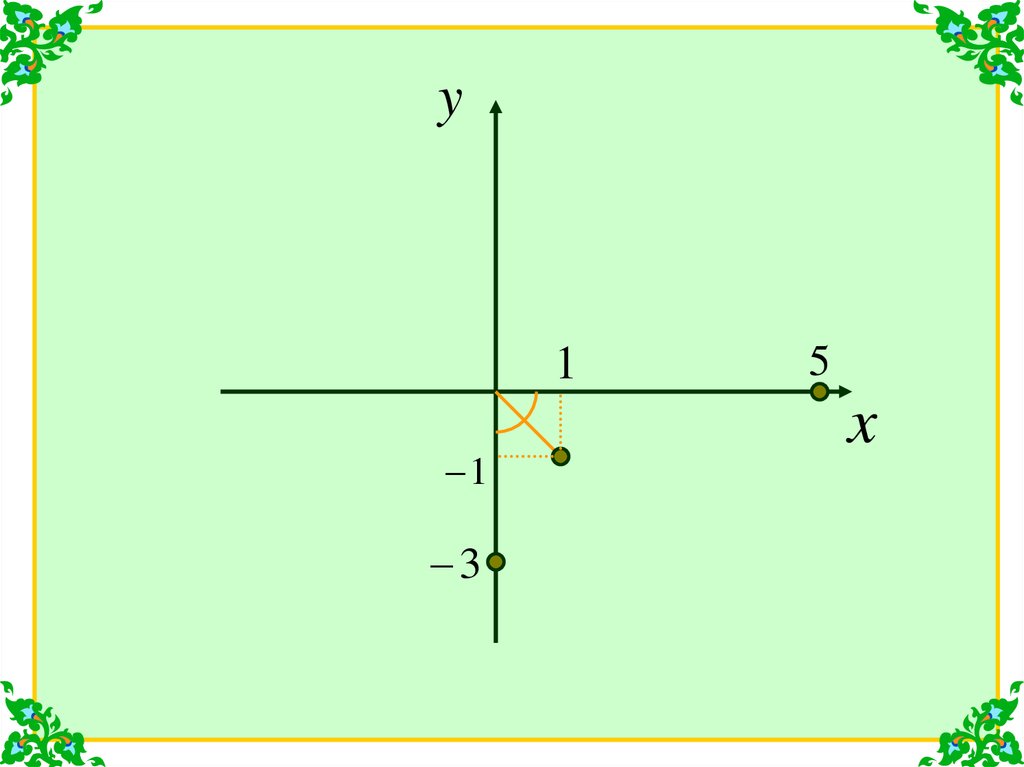
4.

arg 5 0
arg ( 3 i )
arg (1 i )
Поскольку
2
4

5.

y
1
1
3
5
x

6.

Из рисунка видно, что
x r cos
y r sin
Тогда
z x i y r cos i r sin
r (cos i sin )

7.

Выражение
z r (cos i sin )
называется тригонометрической
формой комплексного числа.
2

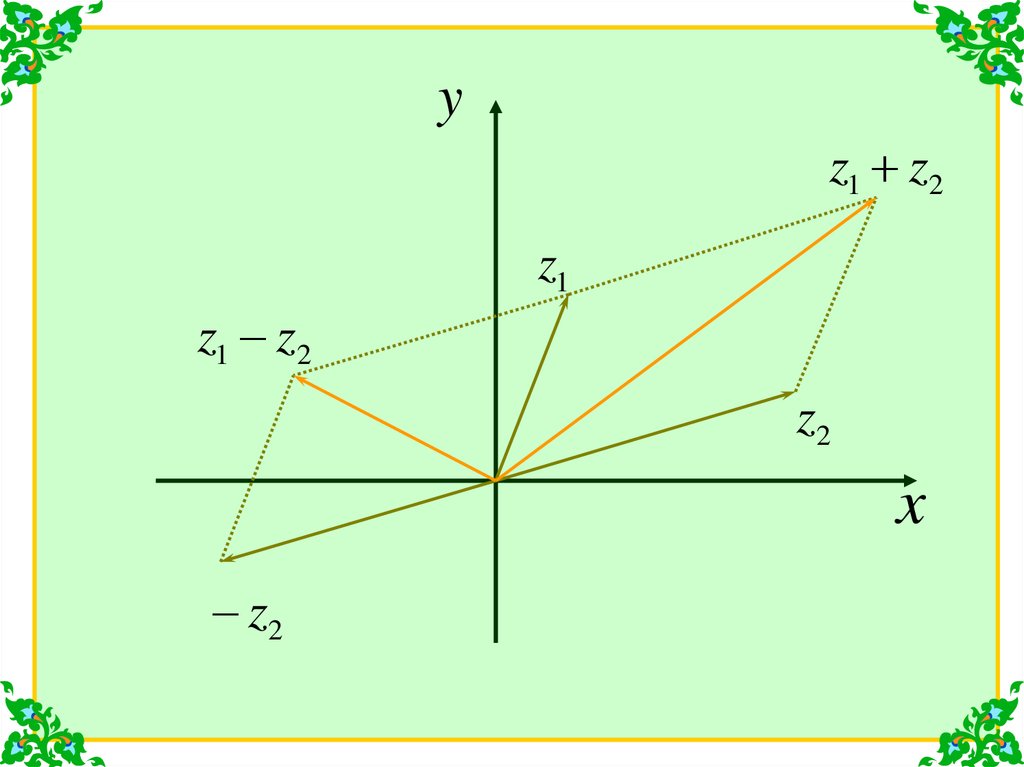
8.

1
При сложении (вычитании) комплексных
чисел, их радиус-векторы складываются
(вычитаются) по правилу параллелограмма.

9.

y
z1 z2
z1
z1 z2
z2
x
z2

10.

2
Модуль произведения (частного) двух
комплексных чисел равен произведению
(частному) модулей этих чисел, а аргумент
- сумме (разности) аргументов этих чисел.

11.

Если
z z1 z2
тогда
z r1 r2 z1 z2
Argz 1 2 Argz1 Argz2
Если
z1
тогда
z
z2
z1
r1
z
r2
z2
Argz 1 2 Argz1 Argz2

12.

Геометрически умножение числа z1 на число z2
означает изменение длины радиус-вектора r1
(или r2) в r2 (или в r1) раз и его поворот
вокруг точки щ против часовой стрелки на
угол φ2 (или φ1).

13.

Комплексные числа
z1 1 i
z2
3 i
представить в тригонометрической
форме и найти их произведение и
частное.

14.

Найдем модули этих комплексных чисел:
r1 z1
r2 z2
x1 y1 1 1
2
2
x2 y2
2
2
2
3 1 2
Теперь найдем аргументы этих комплексных
чисел:
x r cos
y r sin

15.

x1 r1 cos 1
1
y1 r1 sin 1
1 sin 1
1
cos 1
2
sin 1 1
2 cos 1
3
1 arg z1
4

16.

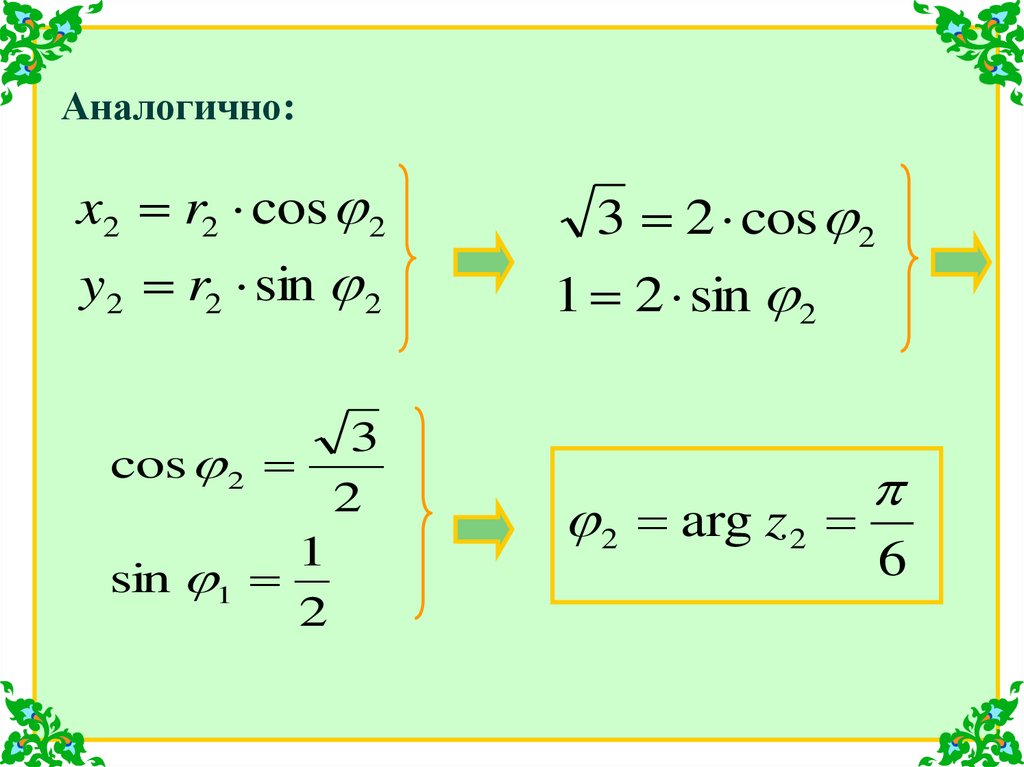
Аналогично:
x2 r2 cos 2
y2 r2 sin 2
3
cos 2
2
1
sin 1
2
3 2 cos 2
1 2 sin 2
2 arg z 2
6

17.

Тогда в тригонометрической форме комплексные
числа запишутся в виде:
z1
3
3
2 cos
i sin
4
4
z 2 2 cos i sin
6
6

18.

Находим их произведение:
3
3
z1 z 2 2 2 cos
i sin
6
6
4
4
11
11
2 2 cos i sin
12
12
Находим их частное:
z1
2
z2
2
3
3
cos
i sin
6
6
4
4
2
7
7
cos i sin
2
12
12

19.

Т.к. при умножении комплексных чисел их
модули перемножаются, а аргументы складываются, то можно получить формулу
возведения
комплексного
числа
в
натуральную степень.
z ( x i y) (r (cos i sin ))
n
n
r (cos n i sin n )
n
n

20.

z r (cos n i sin n )
n
n

21.

Вычислить
( 1 i )
20

22.

Запишем это число
в тригонометрической
форме:
3
3
( 1 i ) 2 cos i sin
4
4
20
3
3
( 1 i ) 2 cos i sin
4
4
3
3
20
( 2 ) cos 20 i sin 20
4
4
1024 (cos 15 i sin 15 ) 1024( 1 0 i ) 1024
20

23.

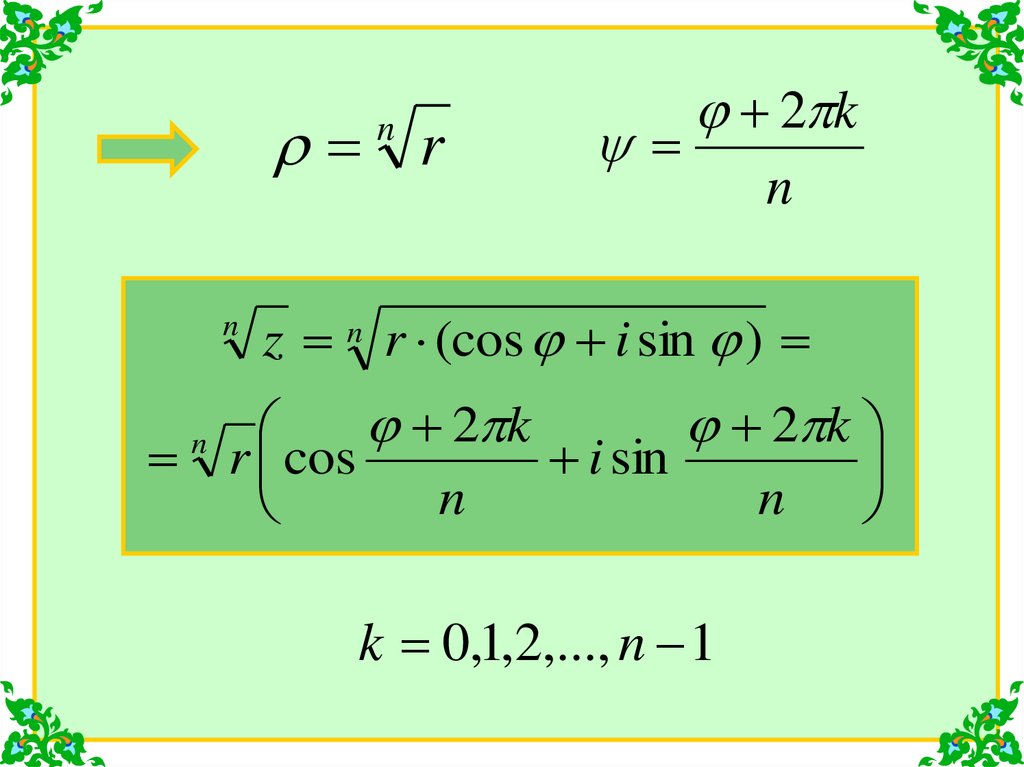
Рассмотрим операцию извлечения корня из
комплексного числа. Пусть
n
тогда
z (cos i sin )
z (cos n i sin n )
n
r (cos i sin )
следовательно
r
n
n 2 k
где k Z

24.

r
n
n
2 k
n
z n r (cos i sin )
2 k
2 k
r cos
i sin
n
n
n
k 0,1,2,..., n 1

25.

Вычислить
3
1 i

26.

3
3
( 1 i ) 2 cos i sin
4
4
3
1 i 3
3
3
2 k
2 k
2 cos 4
i sin 4
3
3
k 0,1,2
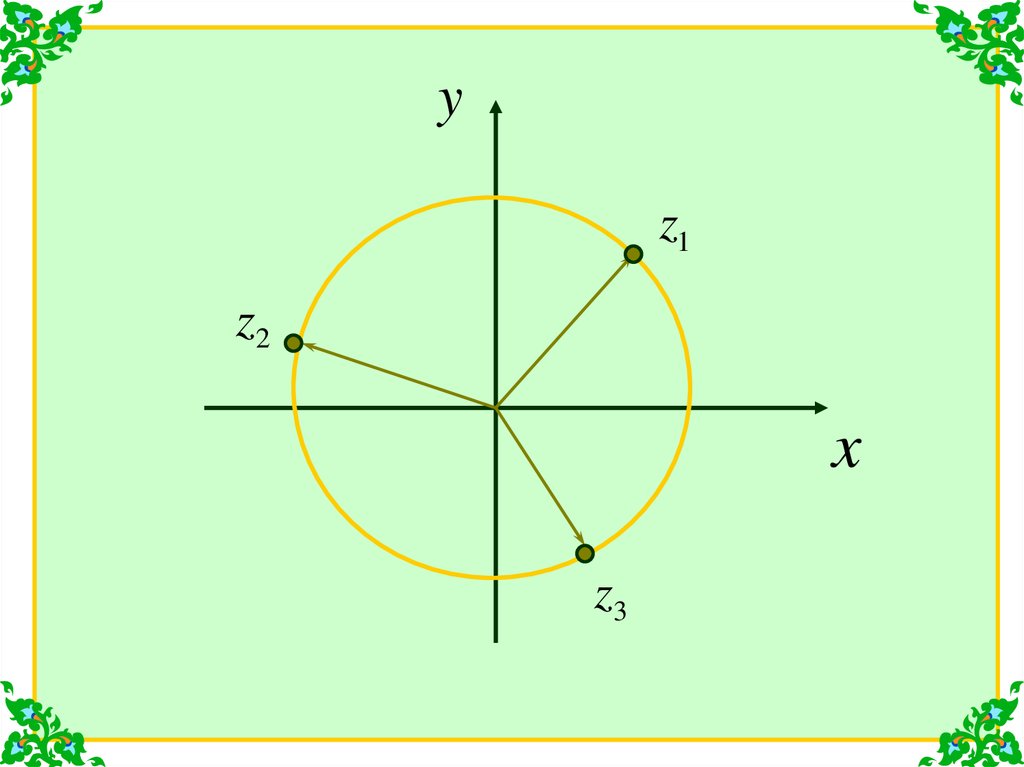
Следовательно, получается три значения корня:

27.

k 0 : z1
k 1 : z2
k 2 : z3
3
3
3
1 i 1 2 cos i sin
4
4
1 i
6
11
11
2 cos
i sin
12
12
19
19
2 cos
i sin
12
12
1 i
6
2
3
6
Изобразим эти точки на комплексной плоскости:

28.

y
z1
z2
x
z3

29.

Точки будут равноудалены друг от друга на
окружности с радиусом 6 2