Множественная регрессия

1. Множественная регрессия

с п е ц и ф и к а ц и я
Множественная
регрессия
L/O/G/O
www.themegallery.com

2. Множественная регрессия

• Уравнение множественной
регрессии в натуральном
масштабе:
yˆ a b1 x1 b2 x2 ... b p x p
– Где Y – зависимая переменная;
– x1, x2,…, xp – независимые переменные;
a и b1, b2,…, bp – параметры (коэффициенты) модели
Напоминание:
Y, x1, x2…xp – изучаемые показатели или явления;
a, b1, b2…bp – числа, характеризующие связь между y и x,
рассчитываются по формулам или в столбце «Коэффициенты» пакета
анализа «Регрессия» в Excel

3. Множественная регрессия

• Регрессионная модель в
стандартизованном масштабе :
t y 1t x1 2t x2 pt x p
– Где t y , t x1 , t x2 ,...,t x p
– стандартизованные переменные;
для которых среднее значение равно нулю, а среднее
квадратическое отклонение равно единице:
ty
y y
y
; tx j
xj xj
xj
,
j 1, n
βj – стандартизованные коэффициенты регрессии, или β –
коэффициенты

4. Расчет:

1
r
1 x1 x 2
1rx1 x p
2 rx 2 x1
3rx3 x1
p rx p x1
ryx1
2 rx 2 x p
3rx3 x p
p
ryx p
2
3rx3 x 2
p rx p x 2
ryx2
Частный случай: наличие 2х факторов x1 и x2
- коэффициенты
корреляции

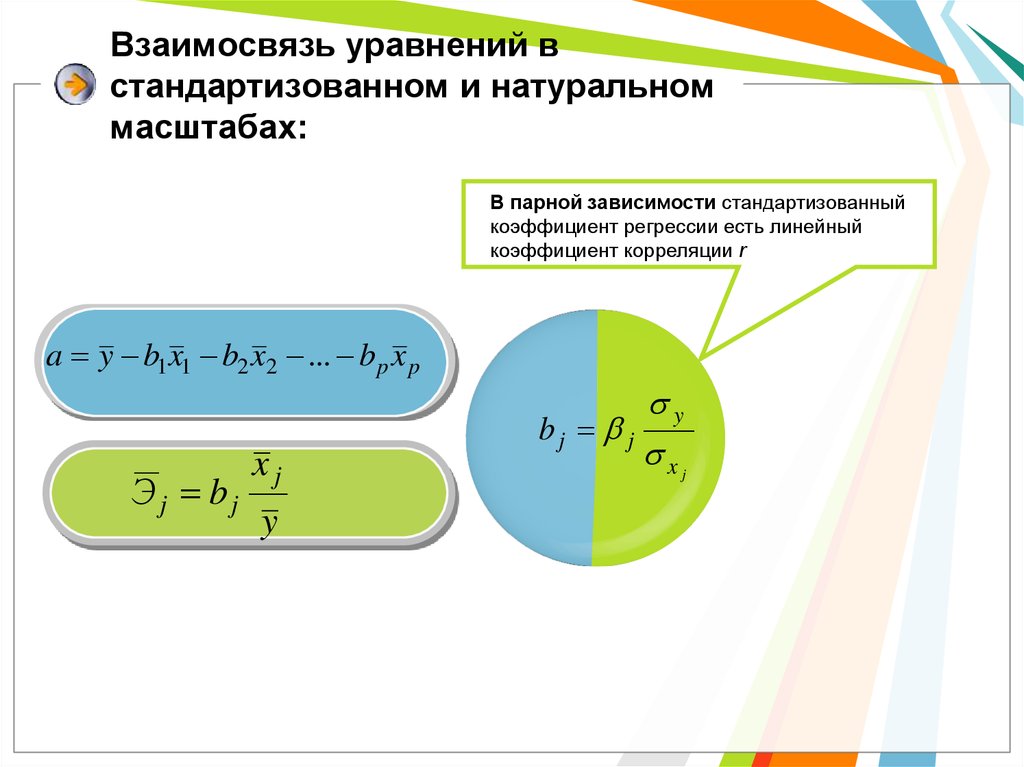
5. Взаимосвязь уравнений в стандартизованном и натуральном масштабах:

В парной зависимости стандартизованный
коэффициент регрессии есть линейный
коэффициент корреляции r
a y b1 x1 b2 x2 ... b p x p
Эj bj
xj
y
y
bj j
xj

6. Интерпретация коэффициентов:

• В модели множественной регрессии в натуральном и
стандартизированном масштабах, а также по эластичности:
b1, b2…bp
показывают на сколько единиц
изменится y при изменении xi на 1
единицу, при неизменности прочих
факторов
β1, β2… βp
на сколько значений с.к.о. изменится в
среднем y, если соответствующий фактор
хj изменится на одну с.к.о. при
неизменном среднем уровне других
факторов
Э1, Э2…Эp
Эластичность показывает на сколько %
в среднем изменится y при изменении
xi на 1%

7. Частная корреляция

Коэффициенты частной корреляции
Частные коэффициенты корреляции характеризуют тесноту связи
между результатом и соответствующим фактором при устранении
влияния других факторов, включенных в уравнение регрессии.
Задача состоит в том, чтобы:
найти «чистую» корреляцию между двумя переменными, исключив
(линейное) влияние других факторов.
Связь с коэффициентом детерминации R2
2
ryx
1 x2
2
R 2 ryx
2
2
1 ryx
2
где ryx2 - обычный коэффициент корреляции
В коэффициенте частной корреляции через точку
указываются факторы, влияние которых
устраняется

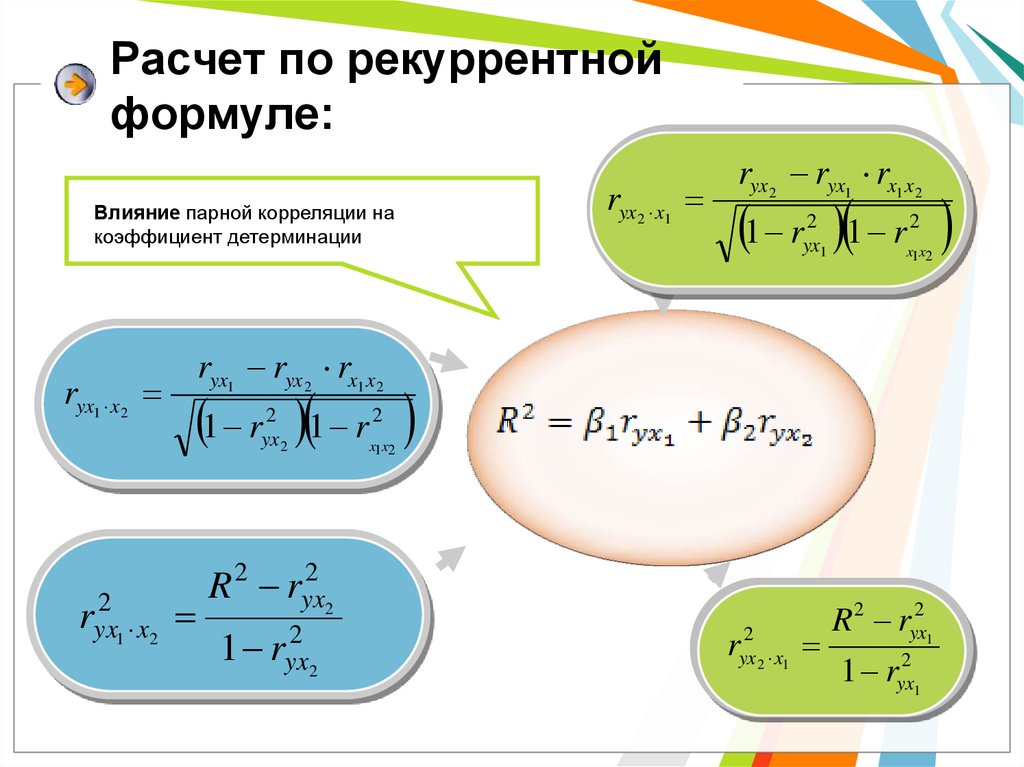
8. Расчет по рекуррентной формуле:

Влияние парной корреляции на
коэффициент детерминации
ryx1 x 2
2
ryx
1 x2
ryx 2 x1
ryx 2 ryx1 rx1 x2
1 r 1 r
2
yx1
2
x1x2
ryx1 ryx 2 rx1 x2
1 r 1 r
2
yx 2
2
x1x2
2
R 2 ryx
2
2
1 ryx
2
ryx2 2 x1
R 2 ryx2 1
1 ryx2 1

9. Тест на обоснованность исключения новых k факторов из модели

Гипотезы:
H 0 : R12 R22
H1 : R12 R22
Наблюдаемое и критическое значение
R12 R22 n p 1
Fнабл
2
1 R1
k
Fкр F ; k ; n p 1
Вывод:
Fнабл<Fкр = H0 (исключение обоснованно)
Fнабл>Fкр то Н1 (исключение не обоснованно)
R1 – коэффициент
детерминации до
исключения;
R2 – коэффициент
детерминации после
исключения;
n – объем выборки;
p – количество
независимых факторов
до исключения;
k – количество
исключаемых факторов

10. Тест на обоснованность включения новых k факторов в модель

Гипотезы:
H 0 : R22 R12
H1 : R22 R12
Наблюдаемое и критическое значение
R22 R12 n p 1
Fнабл
2
1 R2
k
Fкр F ; k ; n p 1
Вывод:
Fнабл<Fкр = H0 (включение не обоснованно)
Fнабл>Fкр то Н1 (включение обоснованно)
R1 – коэффициент
детерминации до
включения;
R2 – коэффициент
детерминации после
включения;
n – объем выборки;
p – количество
независимых факторов
после включения;
k – количество
включаемых факторов

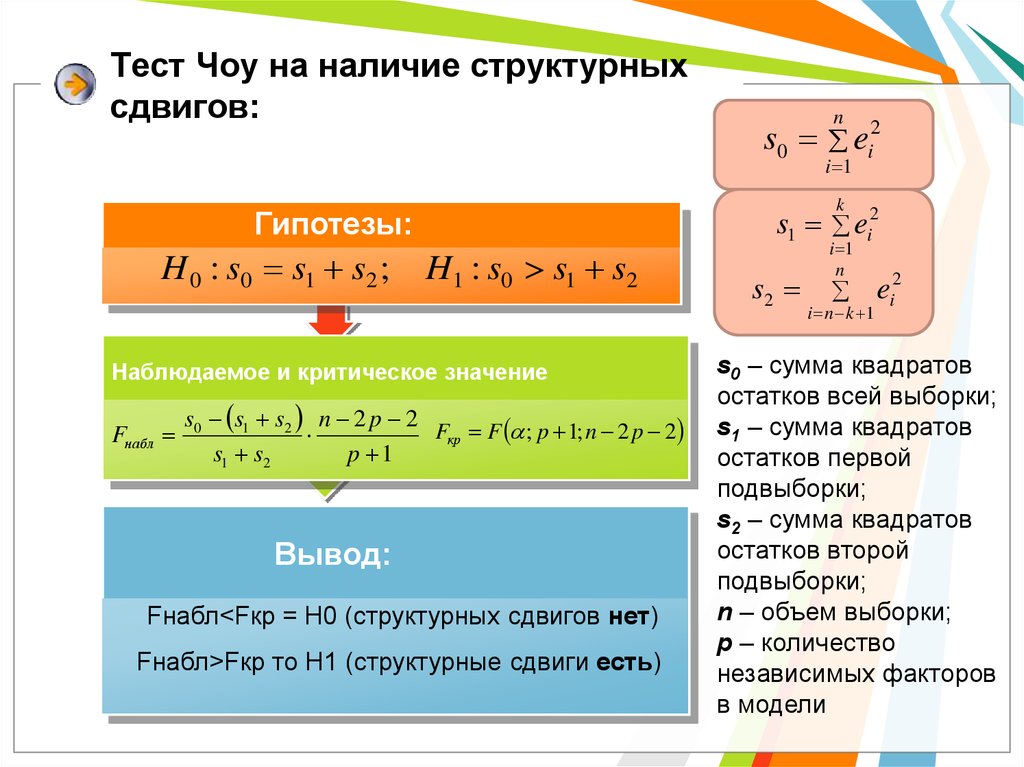
11. Тест Чоу на наличие структурных сдвигов:

n
s0 ei2
i 1
k
Гипотезы:
H 0 : s0 s1 s2 ;
H1 : s0 s1 s2
Наблюдаемое и критическое значение
Fнабл
s0 s1 s2 n 2 p 2
Fкр F ; p 1; n 2 p 2
s1 s2
p 1
Вывод:
Fнабл<Fкр = H0 (структурных сдвигов нет)
Fнабл>Fкр то Н1 (структурные сдвиги есть)
s1 ei2
s2
i 1
n
i n k 1
ei2
s0 – сумма квадратов
остатков всей выборки;
s1 – сумма квадратов
остатков первой
подвыборки;
s2 – сумма квадратов
остатков второй
подвыборки;
n – объем выборки;
p – количество
независимых факторов
в модели

12. Тест Спирмена на наличие гетероскедастичности:

Гипотезы:
H 0 : rx, e 0
H1 : rx ,e 0
Наблюдаемое и критическое значение
tнабл
rx ,e n 2
1 rx2,e
t крит ; n 2
Вывод:
tнабл<tкр = H0 (гомоскедастичность)
tнабл>tкр то Н1 (гетероскедастичность)
rx , e 1 6
n n 2 1
d i2
rx,e– коэффициент
ранговой корреляции
Спирмена;
d – разность рангов xi и
модулей остатков |ei|;

13. Тест Голдфелда – Квандта на наличие гетероскедастичности :

k
Гипотезы:
H 0 : s1 s3 ; H1 : s3 s1
Наблюдаемое и критическое значение
s3
Fнабл
s1
Fкр F ; k p 1; k p 1
Вывод:
Fнабл<Fкр = H0 (гомоскедастичность)
Fнабл>Fкр то Н1 (гетероскедастичность)
s1 ei2
i 1
s3
n
i n 2 k 1
ei2
s1 – сумма квадратов
остатков первой
подвыборки;
s2 – сумма квадратов
остатков второй
подвыборки;
k – объем подвыборки;
p – количество
независимых факторов
в модели

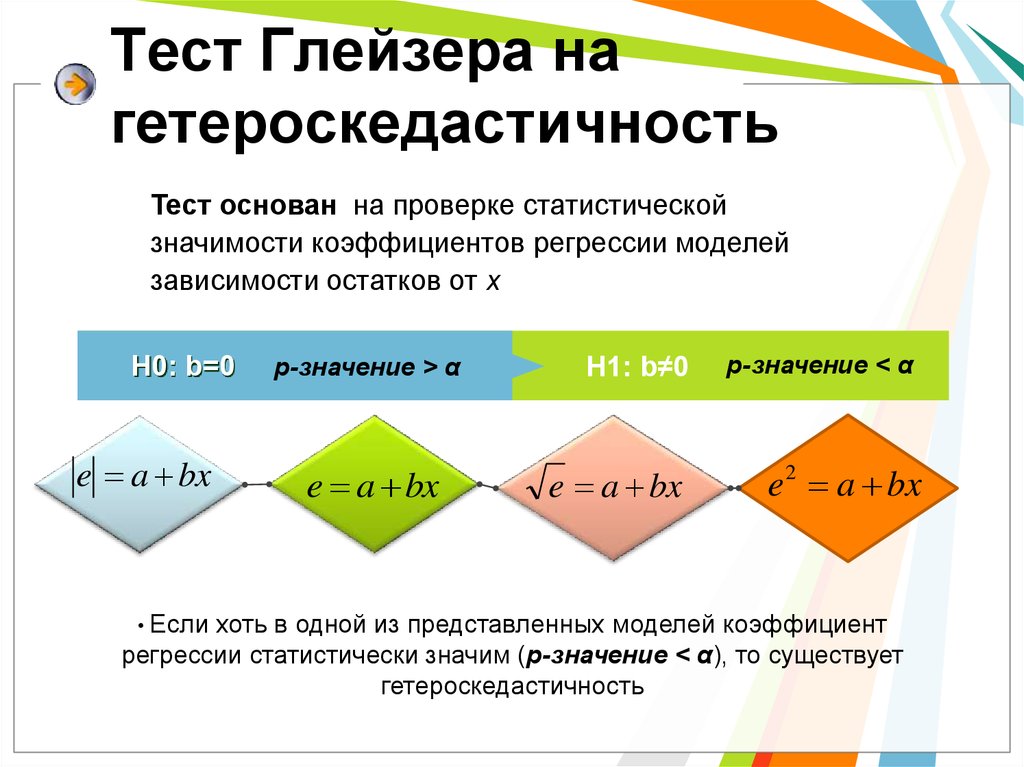
14. Тест Глейзера на гетероскедастичность

Тест основан на проверке статистической
значимости коэффициентов регрессии моделей
зависимости остатков от x
H0: b=0
e a bx
• Если
p-значение > α
e a bx
H1: b≠0
e a bx
p-значение < α
e 2 a bx
хоть в одной из представленных моделей коэффициент
регрессии статистически значим (p-значение < α), то существует
гетероскедастичность

15. Корректировка гетероскедастичности Метод взвешенных наименьших квадратов

.
Корректировка гетероскедастичности
Метод взвешенных наименьших квадратов
• Предпосылка:
Пересчитываются коэффициенты модели линейной регрессии если известны
2
дисперсии остатков для каждого наблюдения
i
.
Ввод новых
переменных
Оценка
параметров
регрессии
Возврат к
исходной
модели
y
*
i
yi
i
; x
*
i
xi
i
; zi
1
i
y* az bx*
*свободный член равен нулю (константа-ноль)
y a bx
*модель гомоскедастична

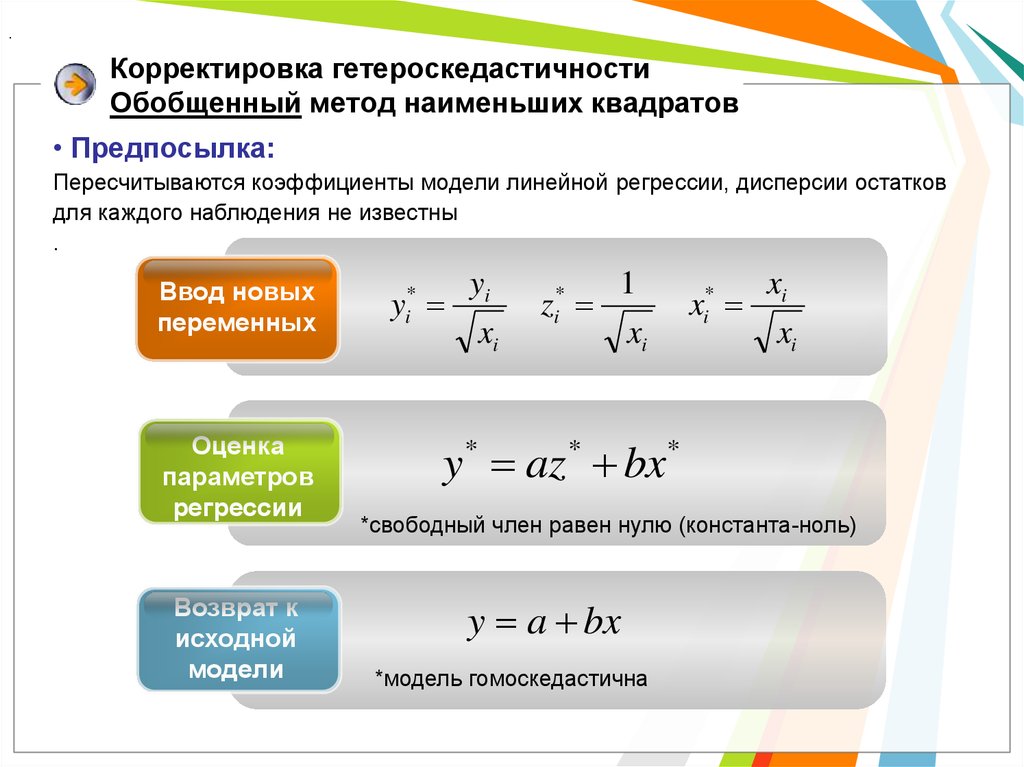
16. Корректировка гетероскедастичности Обобщенный метод наименьших квадратов

.
Корректировка гетероскедастичности
Обобщенный метод наименьших квадратов
• Предпосылка:
Пересчитываются коэффициенты модели линейной регрессии, дисперсии остатков
для каждого наблюдения не известны
.
Ввод новых
переменных
Оценка
параметров
регрессии
Возврат к
исходной
модели
yi
y
xi
*
i
1
z
xi
*
i
xi
x
xi
*
i
y * az * bx*
*свободный член равен нулю (константа-ноль)
y a bx
*модель гомоскедастична

17. Тест Дарбина – Уотсона на наличие автокорреляции :

2
et et 1
n
DW
t 2
n
2
et
t 1
отрицательная АКЛЛ
положительная АКЛЛ
Зона неопр.
Зона неопр.
НЕТ АКЛЛ

18. Корректировка автокорреляции Авторегрессионная схема первого порядка AR(1)

.
Корректировка автокорреляции
Авторегрессионная схема первого порядка AR(1)
• Предпосылка:
Применяется для пересчета коэффициентов модели, если автокорреляция вызвана
внутренними свойствами ряда {et}
Определение ρ
и ввод новых
переменных
Оценка
параметров
регрессии
Возврат к
исходной
модели
et et 1
yt* yt yt 1 ; xt* xt xt 1
y a bx
*
t
a*
a
1
*
*
t
y a bx