Правило Лопиталя раскрытия неопределенности вида

1. Правило Лопиталя раскрытия неопределенности вида

0
Правило Лопиталя раскрытия неопределенности вида 0
Если функции f(x) и g(x) непрерывны и дифференцируемы в
окрестности точки x0 кроме, быть может, самой точки x0 и
обращаются в ноль в этой точке f(x0)=g(x0)=0. Пусть g ( x) 0
f ( x)
l , то
в окрестности точки x0. Если xlim
x0 g ( x )
f ( x)
f ( x)
lim
lim
l
x x0 g ( x )
x x0 g ( x )
1.
2.
1 cos 6 x
0
0 lim
x 0
x 0
2x2
lim
lim
x 0
36 x 2
2x
2
2 9
1 cos 6 x
6 sin 6 x
0
0
lim
2
x
0
2x
4x
0
0
lim
x 0
36 cos 6 x
36
9
4
4

2. Правило Лопиталя раскрытия неопределенности вида

Если функции f(x) и g(x) непрерывны и дифференцируемы в
окрестности точки x0 кроме, быть может, самой точки x0 и
пусть в этой окрестности lim f ( x) lim g ( x) и g ( x) 0
x x0
f ( x)
l , то
Если xlim
x0 g ( x )
x x0
f ( x)
f ( x)
lim
lim
l
x x0 g ( x )
x x0 g ( x )
tg 3 x
3 cos 2 5 x
3
1 cos 10 x
lim
lim
1. lim
tg 5 x
5 cos 2 3 x
1 cos 6 x
5
x
x
x
2
2
2
3
10 sin 10 x
sin 10 x
0
lim
lim
5 x
6 sin 6 x
sin 6 x
x
0
2
2
10 cos10 x
5
0
lim
6 cos 6 x
3
x
0
2

3. Возрастание и убывание функции

(необходимое условие возрастания и убывания функции)
Если дифференцируемая на интервале (a,b) функция
y=f(x) возрастает (убывает), то f ( x ) 0 ( f ( x) 0) для
x a, b .
(достаточное условие монотонности функции)
Если функция y=f(x) дифференцируемая на интервале
(a,b) и f ( x ) 0 ( f ( x) 0) x a, b , то эта функция
возрастает (убывает) на интервале (a,b).

4. Выпуклость функции

Отрезком [ x1 , x2 ] называется множество точек,
удовлетворяющих равенству
x x1 (1 ) x2
0 1
x1
x2
x
0 x x2
1 x x1
1
1
1
x1 x2
x x1 x2
2
2
2
2

5. Выпуклость функции

Функция y=f(x) называется выпуклой вниз (вогнутой)
на промежутке X, если для любых двух значений
x1, x2 X из этого промежутка выполняется неравенство
f ( x1 (1 ) x2 ) f ( x1 ) (1 ) f ( x2 ) 0 1
f ( x2 )
y
y=f(x)
f ( x1 )
0
x1
x2
x
Если функция выпукла вниз, то
отрезок, соединяющий любые
точки графика, целиком лежит над
графиком функции.

6. Выпуклость функции

Функция y=f(x) называется выпуклой вверх (выпуклой)
на промежутке X, если для любых двух значений
x1, x2 X из этого промежутка выполняется неравенство
f ( x1 (1 ) x2 ) f ( x1 ) (1 ) f ( x2 ) 0 1
f ( x2 )
y
Если функция выпукла вниз, то
отрезок, соединяющий любые
точки графика, целиком лежит под
графиком функции.
y=f(x)
f ( x1 )
0
x1
x2
x

7. Выпуклость функции

(достаточное условие выпуклости функции вверх(вниз))
Если функция y=f(x) x a, b имеет f ( x) 0( f ( x) 0),
то эта функция выпукла вниз(вверх) на интервале (a,b)

8. Точки перегиба

Точкой перегиба графика непрерывной функции называется
точка, разделяющая интервалы,в которых функция выпукла
вниз и вверх.
(достаточное условие существования точки перегиба)
Если f (x) при переходе через точку x0 , в которой она равна
нулю или не существует меняет знак, то точка x0 является
точкой перегиба ее графика.
y
x
0
x0

9. Максимум и минимум функции

Точка x0 называется точкой максимума функции y=f(x),
если 0 : x : 0 x x0 f ( x) f ( x0 )
Точка x0 называется точкой минимума функции y=f(x),
если 0 : x : 0 x x0 f ( x) f ( x0 )
Максимум(минимум) функции называется экстремумом функции.
Функция может иметь экстремум лишь во внутренних точках
области определения. Поэтому часто экстремум функции
называют локальным экстремумом.

10. Максимум и минимум функции

Для того, чтобы функция y=f(x) имела экстремум в
точке x0 необходимо, чтобы ее производная в этой
точке равнялась нулю f ( x0 ) 0 или не существовала.
Точки, в которых производная функции равна нулю
или не существует, называются критическими.

11. Максимум и минимум функции

(1-ое достаточное условие экстремума)
Если непрерывная функция y=f(x) дифференцируема
в некоторой - окрестности критической точки x0 и
при переходе через нее (слева направо) производная
f (x ) меняет знак с пляса на минус, то x0 - точка
максимума; с минуса на плюс, то x0 - точка минимума.

12. Максимум и минимум функции

y
f ( x) 0
f ( x) 0
0
y
x0
f ( x) 0
f ( x) 0
x
x0 - точка максимума
0
x1
x
x1 - точка минимума

13. Максимум и минимум функции

0. Найти область определения функции y=f(x)
1. Найти критические точки функции y=f(x)
2. Выбрать те, которые являются внутренними
точками области определения функции
3. Исследовать знак производной f (x ) слева и
справа от исследуемой внутренней критической точки
4. Найти экстремумы функции y=f(x)

14. Найти экстремум функции

x 3 2
y x
3
D( y ) : R
1
2
1 3 x 2
y 3 3
3 3 x 3
x
y не существуют при x1 0 и x2 8
-
+
0
+
f (x )
8
x1 0 - точка максимума ymax y(0) 0 - максимум функции
4
x1 8 - точка минимума ymin y (8) - минимум функции
3

15. Максимум и минимум функции

(2-ое достаточное условие экстремума)
Если в точке x0 f ( x0 ) 0 , а f ( x0 ) существует и
f ( x0 ) 0, то если f ( x0 ) 0 , то в точке x0 функция
имеет максимум, если f ( x0 ) 0, то в точке x0 функция
имеет минимум.

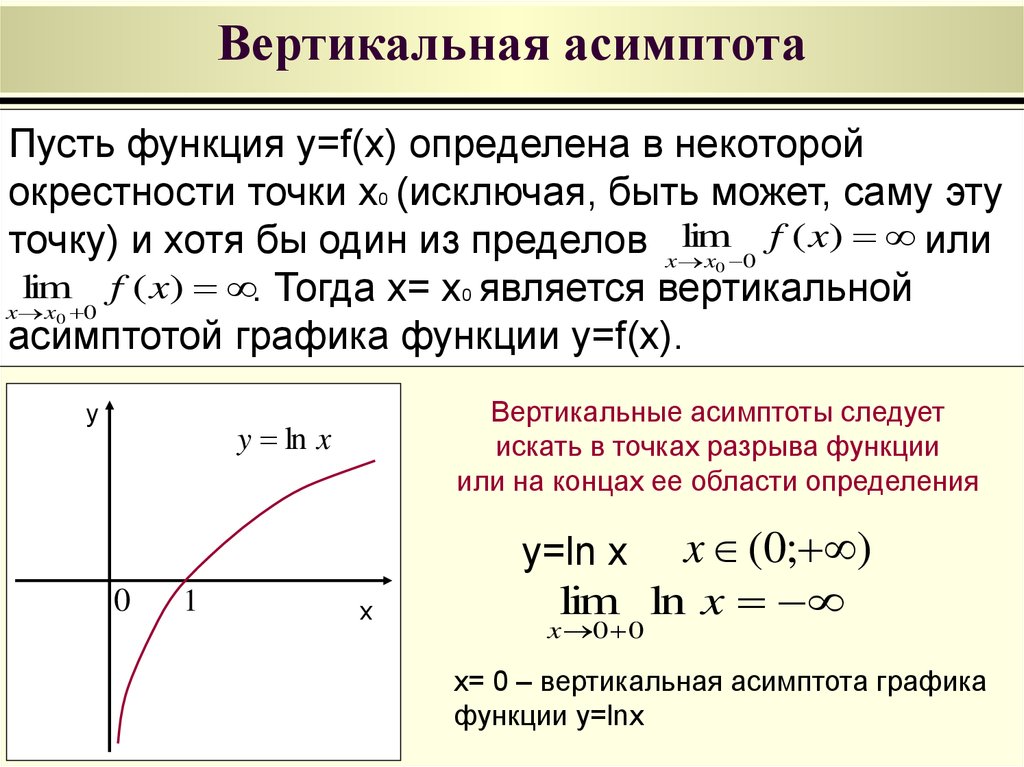
16. Вертикальная асимптота

Пусть функция y=f(x) определена в некоторой
окрестности точки x0 (исключая, быть может, саму эту
lim f ( x) или
точку) и хотя бы один из пределов x
x 0
lim f ( x) . Тогда x= x0 является вертикальной
x x 0
асимптотой графика функции y=f(x).
0
0
y
Вертикальные асимптоты следует
искать в точках разрыва функции
или на концах ее области определения
y ln x
0
1
x
y=ln x x (0; )
lim ln x
x 0 0
x= 0 – вертикальная асимптота графика
функции y=lnx

17. Горизонтальная асимптота

Пусть функция y=f(x) определена при достаточно
f ( x) b .Тогда прямая y=b является
больших x и lim
x
горизонтальной асимптотой графика функции y=f(x).
f ( x) bЛ или lim f ( x) bП
Если конечен только один из пределов xlim
x
то функция имеет лишь левостороннюю y=bл или правостороннюю y=bп
горизонтальную асимптоту.
x
y
y ex
y e
lim e x 0
x
1
0
y= 0 – левосторонняя горизонтальная
x
асимптота графика функции y e
x

18. Наклонная асимптота

Если
lim f ( x )
x
функция может иметь наклонную асимптоту.
Пусть функция y=f(x) определена при достаточно
f ( x)
lim
больших x и существуют конечные пределы x x k
( f ( x) kx) b. Тогда y=kx+b является наклонной
и lim
x
асимптотой графика функции y=f(x).
Наклонная асимптота так же может быть правосторонней или
левосторонней.

19. Исследование на наличие асимптот

y x e
x
Так как D( y ) : ( ; ) , то вертикальных асимптот нет
, x
f ( x)
x ex
x
k lim
lim
lim e
x
x
x
x
x
0, x
x
1
lim ( f ( x) kx) lim x e lim x lim
0
x
x
x
x e
x
e
x
y=0 – горизонтальная левосторонняя асимптота

20. Исследование на наличие асимптот

2
x
y
x 1
x2
lim
Так как D( y ) : ( ;1) (1; ) и x 1 0 x 2 1
x
lim
x 1 0 x 1
, то
x 1 0
x=1 – вертикальная асимптота при
x 1 0
k lim
x
f ( x)
x
lim
x x 1
x
1
lim
x 1 1
x2
x2 x2 x
x
lim ( f ( x) kx) lim (
x) lim
lim
1
x
x x 1
x
x x 1
x 1
y=x+1 – наклонная асимптота при x

21. Общая схема исследования функции и построения графика

Найти область определения функции
Найти (если возможно) точки пересечения графика с
осями координат
Найти интервалы знакопостоянства функции
Исследовать функцию на четность (нечетность)
Найти асимптоты графика функции
Найти интервалы монотонности функции
Найти экстремумы функции
Найти интервалы выпуклости и точки перегиба
графика функции

22. Исследовать функцию и построить ее график

y x 3x
3
3
2
1. D( y ) ( ; )
2. Точки пересечения с осями координат
OX: y=0 3 x3 3x 2 0
x ( x 3) 0
x1 0; x2 3
2
(0,0); (3,0) - точки пересечения с осью OX
2
3 3
f
(
0
)
0
3
0
0
OY: x=0
(0,0) - точка пересечения с осью OY
3. f ( x) 0 x 2 ( x 3) 0 x (3; )
f ( x) 0 x 2 ( x 3) 0 x ( ;0) (0;3)

23. Исследовать функцию и построить ее график

4. f ( x) 3 x 3 3x 2
f ( x) 3 ( x)3 3( x) 2 3 x 3 3x 2
f ( x) f ( x); f ( x) f ( x) - функция ни четна, ни нечетна
5. Вертикальных асимптот нет, так как функция непрерывна
3
2
3 3
3
lim x 3x lim x 1 горизонтальных асимптот нет
x
x
x
3
2
3
x 3x
3
3
k lim
lim 1 1
x
x
x
x
3
2
3
x
3
x
x
b lim (3 x 3 3x 2 x) lim
x
x 3
( x 3 3x 2 ) 2 x3 x 3 3x 2 x 2
3
lim
x
( x 3x )
3
3
1 1
6
x
x
3
3
2 2
1
наклонная асимптота
y x 1

24. Исследовать функцию и построить ее график

1 3x 2 6 x
x( x 2)
6. y
3 3 ( x 3 3x 2 ) 2 3 ( x 3 3x 2 ) 2
y 0 при x1 0; x2 2
y не существует при x 3
-
+
0
+
2
+
3
f (x )
x
x 0 - точка максимума ymax y(0) 0 - максимум функции
3
y
y
(
2
)
4- минимум функции
x 2 - точка минимума min

25. Исследовать функцию и построить ее график

7. y
2
4
3
x ( x 3)
5
3
y не существует при x1 0; x2 3
-
+
0
x 0 y (0) 0
x 3 y (3) 0
3
- точки перегиба
f (x)
x

26. Исследовать функцию и построить ее график

y x 3x
3
y
0
1
-1
2
3
3
2
x