Похожие презентации:
Асимметричные алгоритмы. Продолжение
1. Асимметричные алгоритмы. Продолжение.
2.
Схема Диффи-ХеллманаПредположим, что обоим абонентам известны некоторые два числа g и p
(например, они могут быть «зашиты» в программное обеспечение),
которые не являются секретными и могут быть известны также другим
заинтересованным лицам. Для того, чтобы создать неизвестный более
никому секретный ключ, оба абонента генерируют большие случайные
числа: первый абонент — число a, второй абонент — число b. Затем
первый абонент вычисляет значение A = gamod p и пересылает его
второму, а второй вычисляет B = gbmod p и передаёт первому.
Предполагается, что злоумышленник может получить оба этих значения,
но не модифицировать их (то есть у него нет возможности вмешаться в
процесс передачи). На втором этапе первый абонент на основе
имеющегося у него a и полученного по сети B вычисляет значение Bamod
p = gabmod p, а второй абонент на основе имеющегося у него b и
полученного по сети A вычисляет значение Abmod p = gabmod p. Как
нетрудно видеть, у обоих абонентов получилось одно и то же число: K =
gabmod p. Его они и могут использовать в качестве секретного ключа,
поскольку здесь злоумышленник встретится с практически
неразрешимой (за разумное время) проблемой вычисления gabmod p по
перехваченным gamod p и gbmod p, если числа p,a,b выбраны
достаточно большими.
3.
При работе алгоритма, каждая сторона:генерирует случайное натуральное число a — закрытый ключ
совместно с удалённой стороной устанавливает открытые параметры
p и g (обычно значения p и g генерируются на одной стороне и
передаются другой), где
p является случайным простым числом
g является первообразным корнем по модулю p
вычисляет открытый ключ A, используя преобразование над
закрытым ключом
A = ga mod p
обменивается открытыми ключами с удалённой стороной
вычисляет общий секретный ключ K, используя открытый ключ
удаленной стороны B и свой закрытый ключ a
K = Ba mod p
К получается равным с обеих сторон, потому что:
Ba mod p = (gb mod p)a mod p = gab mod p = (ga mod p)b mod p = Ab
mod p
В практических реализациях, для a и b используются числа порядка
10100 и p порядка 10300. Число g не обязано быть большим и обычно
имеет значение в пределах первого десятка.
4.
Алгоритм Диффи-Хеллмана работает на линиях связи, надежно защищенныхот модификации. Однако, в тех случаях, когда в канале возможна
модификация данных, появляется очевидная возможность вклинивания в
процесс генерации ключей "злоумышленника-посредника".
Для защиты используются различные варианты надежной аутитификации.
Атака с подставкой (Man-in-the-middle attack): Две стороны обмениваются
ключами для секретной коммуникации. Противник внедряется между ними
на линии обмена сообщениями. Далее противник выдает каждой стороне
свои ключи. В результате, каждая из сторон будет иметь разные ключи,
каждый из которых известен противнику. Теперь противник будет
расшифровывать каждое сообщение своим ключом и затем зашифровывать
его с помощью другого ключа перед отправкой адресату. Стороны будут
иметь иллюзию секретной переписки, в то время как на самом деле
противник читает все сообщения.
Одним из способов предотвратить такой тип атак заключается в том, что
стороны при обмене ключами вычисляют криптографическую хэш-функцию
значения протокола обмена (или по меньшей мере значения ключей),
подписывают ее алгоритмом цифровой подписи и посылают подпись другой
стороне. Получатель проверит подпись и то, что значение хэш-функции
совпадает с вычисленным значением. Такой метод используется, в
частности, в системе Фотурис (Photuris).
5.
Криптографическая стойкость алгоритма Диффи — Хеллмана (то естьсложность вычисления K=gab mod p по известным p, g, A=ga mod p и
B=gb mod p), основана на предполагаемой сложности проблемы
дискретного логарифмирования.
6.
Схема Эль-ГамаляСхема Эль-Гамаля (Elgamal) — криптосистема, предложенная в 1984
году. Схема Эль-Гамаля лежит в основе стандартов электронной
цифровой подписи в США и России.
7.
Генерация ключейГенерируется случайное простое число p длины n.
Выбирается произвольное целое число g, являющееся первообразным
корнем по модулю p.
Выбирается случайное число x из интервала (1,p).
Вычисляется y = gx mod p.
Открытым ключом является тройка (p,g,y),
закрытым ключом — число x.
8.
ШифрованиеСообщение М шифруется так:
Выбирается случайное секретное число k из отрезка [1, p-2].
Вычисляется a = gk mod p, b = yk M mod p,
где M — исходное сообщение.
Пара чисел (a,b) является шифротекстом.
Длина шифротекста в схеме Эль-Гамаля длиннее исходного сообщения M
вдвое.
Дешифрование
Зная закрытый ключ x, исходное сообщение можно вычислить из
шифротекста (a,b) по формуле:
При этом нетрудно проверить, что
и .
9.
Криптостойкость данной схемы основана на вычислительнойсложности проблемы дискретного логарифмирования, где по
известным p, g и y требуется вычислить х, удовлетворяющий
сравнению:
10.
Эллиптические кривые описываются уравнениемy 2 axy by x 3 cx 2 dx e
11.
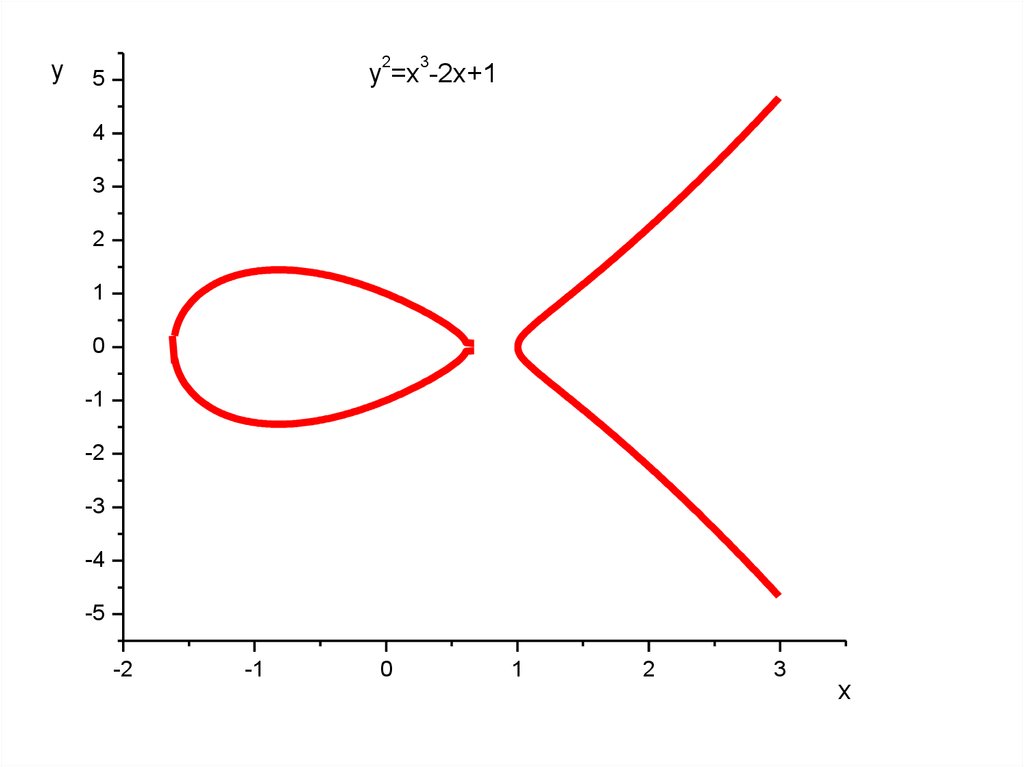
y2
3
y =x -2x+1
5
4
3
2
1
0
-1
-2
-3
-4
-5
-2
-1
0
1
2
3
x
12.
y =x -2x+15
y2=x3+ax+b
4
A={x,y}
3
2
1
0
-1
-2
-A={x,-y}
-3
-4
-5
-2
-1
0
1
2
3
x
13.
y2
3
y =x -2x+1
5
4
C
3
B
2
A
1
0
-1
A'
-2
B'
-3
C'
-4
-5
-2
-1
0
1
2
3
x
14.
Oy
2
3
y =x -2x+1
5
4
A
3
2
1
0
-1
-2
A'
-3
-4
-5
-2
-1
0
1
2
3
x
15.
y2
3
y =x -2x+1
5
4
3
A
2
1
0
-1
-2
-3
2A
-4
-5
-2
-1
0
1
2
3
x
16. Сложение
1. Сложение с нулевым элементом ( несобственной точкой O)A A O A
2. Противоположные точки A x; y , A x; y
A-A=O
3. Если точки P и Q не удовлетворяют условиям 1 и 2, то прямая, проведенная через эти
две точки имеет еще ровно одну точку пересечения с эллиптической кривой. Эта
точка называется суммой точек P и Q. В вырожденном случае, когда прямая,
проведенная через две точки P и Q , является касательной к одной из этих точек
(например Q), то суммой точек P и Q является точка -Q.
4. Сложение точки самой с собой Q+Q. Проводится касательная к точке Q, ищется
точка пересечения касательной с эллиптической кривой S и в качастве суммы
берется точка, противоположная к S:
Q+Q=2Q= - S
17.
коммутативный и ассоциативный законыQ+Q=2Q= - S
k P P P ...P
18.
Эллиптическая группа по модулю p.Эллиптическая группа по модулю p E p a, b
для простого числа p и натуральных чисел a и b
(должно выполняться условие 4a 3 27b 2 mod p 0 )
– множество, элементами которого являются
1) несобственная точка O
2) точки x; y ,
3) координаты которых удовлетворяют следующим условиям:
0 x p 1
0 y p 1
( y 2 ) mod p ( x 3 ax b) mod p
19.
E 23 1,1 .В этом случае
p 23
a 1
b 1
(4a 3 27b 2 ) mod p 31 mod 23 8 0
Координата x - 0,1,2 …,22.
Для каждого из этих значений x вычисляется
3
( x 1 x 1) mod 23
20.
x0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
( x 3 ax b) mod p
1
3
11
8
0
16
16
6
15
3
22
9
16
3
22
10
19
9
9
2
17
14
22
21.
x0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
x*x
0
1
4
9
16
2
13
3
18
12
8
6
6
8
12
18
3
13
2
16
9
4
1
0,1,2,3,4,6,8,9,12,13,16,18
22.
x0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
( x 3 ax b) mod p
1
3
11
8
0
16
16
6
15
3
22
9
16
3
22
10
19
9
9
2
17
14
22
y1
y2
1
7
22
16
10
0
4
4
11
13
7
16
3
4
7
20
19
16
3
3
5
20
20
18
19
19
12
23.
E 23 1,1 состоит из следующих точек:O;
0,1 ; 0,22 ; 1,7 ; 1,16 ; 3,10 ; 3,13 ; 4,0 ; 5,4 ; 5,19 ; 6,4 ; 6,19 ; 7,11 ; 7,12 ; 9,7 ; 9,16 ; 11,3 ; 1
12,4 ; 12,19 ; 13,7 ; 13,16 ; 17,3 ; 17,20 ; 18,3 ; 18,20 ; 19,5 ; 19,18
24.
Правила сложения точек в E p a, b :1. P E p a, b P O P
2. P P O; P x; y ; P x; y
3.В остальных случаях сложение точек P x1 ; y1 и Q x2 ; y2 определяется
следующим образом:
P Q x3 ; y 3
x3 2 x1 x 2 mod p
y 3 x1 x3 y1 mod p
y 2 y1
x x mod p, если P Q
2
1
2
3x 1 a mod p, если P Q
2 y1
25.
Пример 1P 3;10 ; Q 9;7
7 10
3
1
P Q
mod 23
mod 23 mod 23 11
9 3
6
2
x3 112 3 9 mod 23 109 mod 23 17
y 3 11 3 6 10 mod 23 89 mod 23 20
P Q 17;20
26.
Пример 2P 3;10
2P ?
3 32 1
5
1
mod 23
mod 23 mod 23 6
2 10
20
4
x3 6 2 3 9 mod 23 30 mod 23 7
y 3 6 3 7 10 mod 23 34 mod 23 12
2 P 7;12
27.
Q kP .1. Выбираем простое число p и параметры a и b для эллиптической группы точек
E p a, b .
2. Выбираем генерирующую точку G x1 ; y1 . При выборе G важно, чтобы nG=0
при достаточно большом значении n.
Параметры E p a, b и G известны всем участникам. Обмен ключами между
абонентами A и B происходит следующим образом.
1. A выбирает целое число n A , меньшее n ( Это личный ключ A).
A вычисляет PA n AG . Эта точка из E p a, b - публичный ключ A
B выбирает целое число n B , меньшее n ( Это личный ключ B).
B вычисляет PB nB G . Эта точка из E p a, b - публичный ключ B
2. A и B обмениваются своими публичными ключами по открытому каналу
связи.
3. A вычисляет общий ключ – точку из E p a, b : K n A PB
B вычисляет общий ключ : K nB PA
28.
Квантовое распространение ключа29.
Принцип неопределенности ГейзенбергаКвантовый объект:
1. Измерение изменяет состояния объекта.
2. Невозможно получить полную информацию о квантовом
объекте, и следовательно, невозможно его скопировать.
А
B
E
А
B
E
В квантовой криптографии копирование невозможно, а любая
попытка прослушать линию приводит к изменению состояния
фотонов, что немедленно сигнализирует о вмешательстве в связь
двух общающихся сторон.
30.
Квантовое распространение ключаСостояние квантового объекта (то есть, объекта очень малой массы и размеров, например,
электрона или фотона) может быть определено измерением. Однако сразу после
выполнения этого измерения квантовый объект неизбежно переходит в другое состояние,
причем предсказать это состояние невозможно. Следовательно, если в качестве носителей
информации использовать квантовые частицы, то попытка перехватить сообщение
приведет к изменению состояния частиц, что позволит обнаружить нарушение
секретности передачи. Кроме того, невозможно получить полную информацию о
квантовом объекте, и следовательно, невозможно его скопировать. Эти свойства
квантовых объектов делают их «неуловимыми».
Идея использовать квантовые объекты для защиты информации от подделки и
несанкционированного доступа впервые была высказана Стефаном Вейснером (Stephen
Weisner) в 1970 г. Спустя 10 лет Беннет и Брассард, которые были знакомы с работой
Вейснера, предложили использовать квантовые объекты для передачи секретного ключа.
В 1984 г. они опубликовали статью, в которой описывался протокол квантового
распространения ключа ВВ84.
31.
Идея использовать квантовые объекты для защиты информации отподделки и несанкционированного доступа впервые была высказана
Стефаном Вейснером (Stephen Weisner) в 1970 г.
Спустя 10 лет Беннет и Брассард, которые были знакомы с работой
Вейснера, предложили использовать квантовые объекты для
передачи секретного ключа. В 1984 г. они опубликовали статью, в
которой описывался протокол квантового распространения ключа
ВВ84.
32.
Носителями информации в протоколе ВВ84 являются фотоны, поляризованные подуглами 0, 45, 90, 135 градусов. В соответствии с законами квантовой физики, с помощью
измерения можно различить лишь два ортогональных состояния: если известно, что фотон
поляризован либо вертикально, либо горизонтально, то путем измерения, можно
установить — как именно; то же самое можно утверждать относительно поляризации под
углами 45 и 135 градусв. Однако с достоверностью отличить вертикально поляризованный
фотон от фотона, поляризованного под углом 45?, невозможно.
33.
10
1
0
34.
11
A
B
?
A
B
35.
A:10110…
B:
01100…
36.
B располагает двумя анализаторами: один распознает вертикально-горизонтальнуюполяризацию, другой — диагональную. Для каждого фотона B случайно выбирает один из
анализаторов и записывает тип анализатора и результат измерений.
По общедоступному каналу связи B сообщает А, какие анализаторы использовались, но не
сообщает, какие результаты были получены.
А по общедоступному каналу связи сообщает B, какие анализаторы он выбрал правильно.
Те фотоны, для которых B неверно выбрал анализатор, отбрасываются.
37.
Фильтр A1
0
1
1
0
0
0
1
0
Ключевая последовательность
1
1
0
1
0
0
1
1
1
Последовательность фотонов
|
\
/
|
-
-
\
|
\
Измеритель B
1
1
0
0
0
1
0
1
1
Результат измерения B
1
0
0
1
0
1
1
1
0
-
-
-
Измерители выбраны верно
Ключ
+
1
+
0
-
+
+
1
1
-
38.
Экспериментальная реализация1989 г. В Уотсоновском исследовательском центре IBM Чарльзом
Беннетом, Джилом Брасардом и их студентами была построена
первая система - 10 бит/с на расстоянии 30 см.
24.07.2009 Исследователи из Университета Женевы (University
of Geneva) в Швейцарии и Corning Inc. продемонстрировали
новый QKD-прототип, который может распределять квантовые
ключи на расстоянии 250 км в лабораторных условиях.
20.04. 2010 Создана рекордно быстрая система распространения
квантовых ключей со скоростью, превышающей 1 Мбит/с.





































 Математика
Математика








