Производная функции в точке

1.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Лекция 1
ПРОИЗВОДНАЯ ФУНКЦИИ
В ТОЧКЕ

2.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производная функции в точке
Пусть функция f (x) определена в некоторой окрестности
точки х0.
Определение 1:
Производной функции f (x) в точке x0 называется число,
обозначаемое f ’(x0), равное пределу отношения
f ( x) f ( x0 )
x x0
при x x0
если этот предел существует.
f ( x) f ( x0 )
f ( x0 ) lim
x x0
x x0

3.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производная функции в точке
Определение 2:
Производная функции f (x) в точке x0 есть предел отношения
её приращения f ( x0 ) к соответствующему приращению
её аргумента x
f ( x0 ) lim
x 0
при x 0
f ( x0 x) f ( x0 )
f ( x0 )
lim
x
x 0 x
Обозначения:
Производную функции y = f (x) принято обозначать так:
y ( x0 );
y x ( x0 );
df ( x0 ) dy( x0 )
f x ( x0 );
;
.
dx
dx

4.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Односторонние производные функции в точке
Правая производная:
Если функция f (x) определена в некоторой правой
полуокрестности точки x0 , то её правой производной
называется предел
f ( x0 0) f ( x0 )
lim
x x0 0
f ( x) f ( x0 )
f ( x0 )
lim
x x0
x 0 x
Левая производная:
Если функция f (x) определена в некоторой левой
полуокрестности точки x0 , то её левой производной
называется предел
f ( x0 0) f ( x0 )
lim
x x0 0
f ( x) f ( x0 )
f ( x0 )
lim
x x0
x 0 x

5.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производная функции в точке
Пример 1:
Найти производную функции
e x sin 5 x 1, x 0
f ( x)
x 0
0,
в точке х0 = 0.
Пример 2:
Найти производную функции
в точках х1 = 0 и х2 = 1.
f ( x) | x 1 |

6.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производная функции в точке
Теорема:
Если функция f (x) имеет производную в точке x0, то она
непрерывна в точке x0.
Обратное утверждение неверно.

7.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
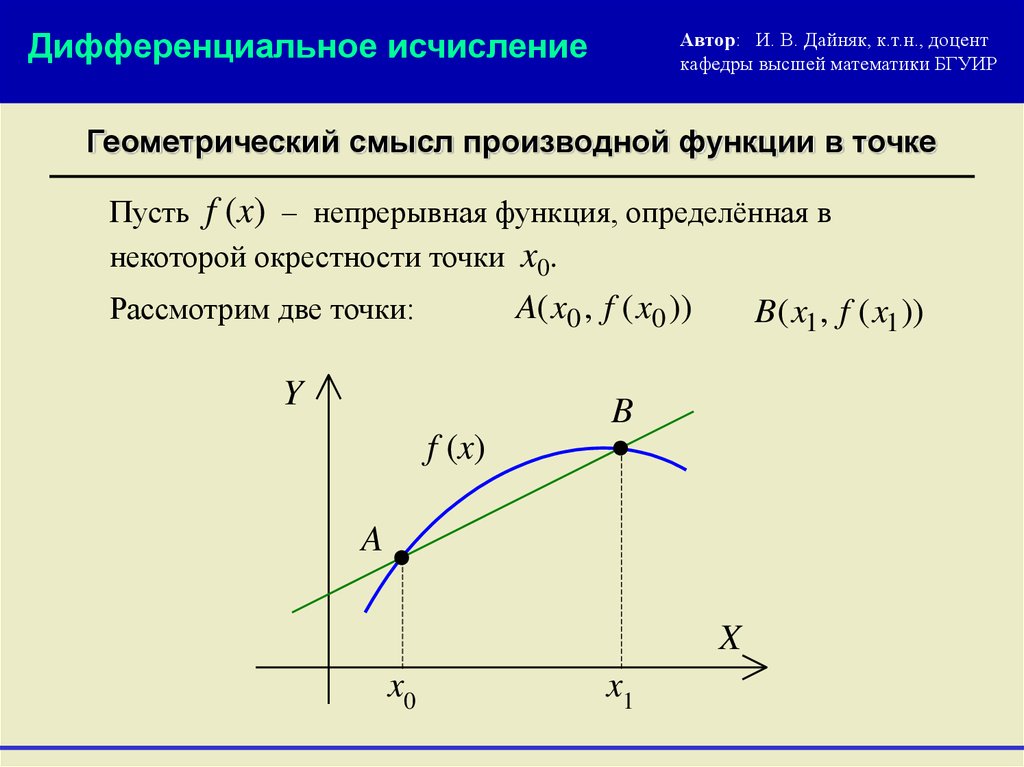
Геометрический смысл производной функции в точке
Пусть f (x) – непрерывная функция, определённая в
некоторой окрестности точки x0.
Рассмотрим две точки:
A( x0 , f ( x0 ))
Y
B ( x1, f ( x1 ))
B
f (x)
A
X
x0
x1

8.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
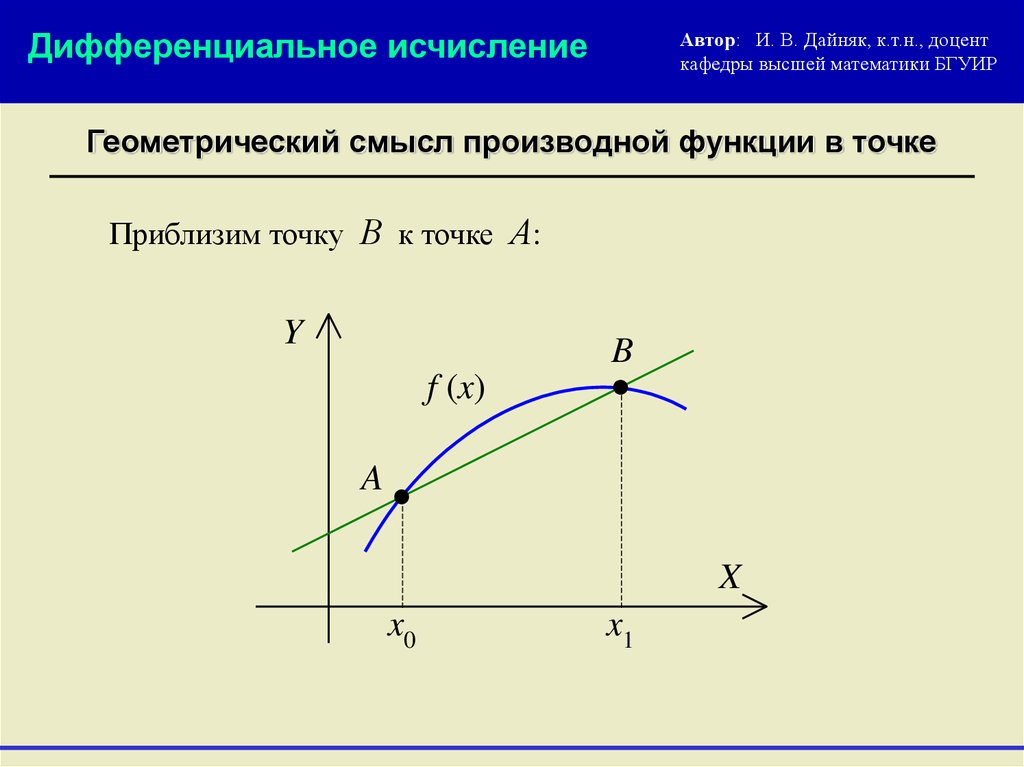
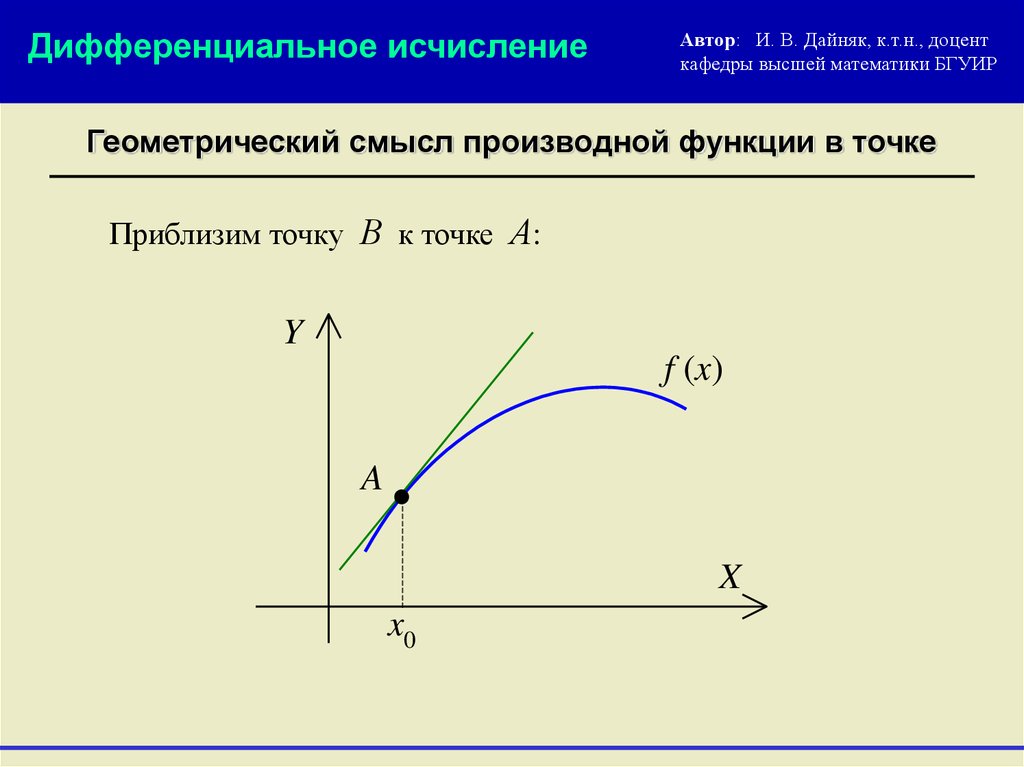
Геометрический смысл производной функции в точке
Приблизим точку В к точке А:
Y
B
f (x)
A
X
x0
x1

9.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
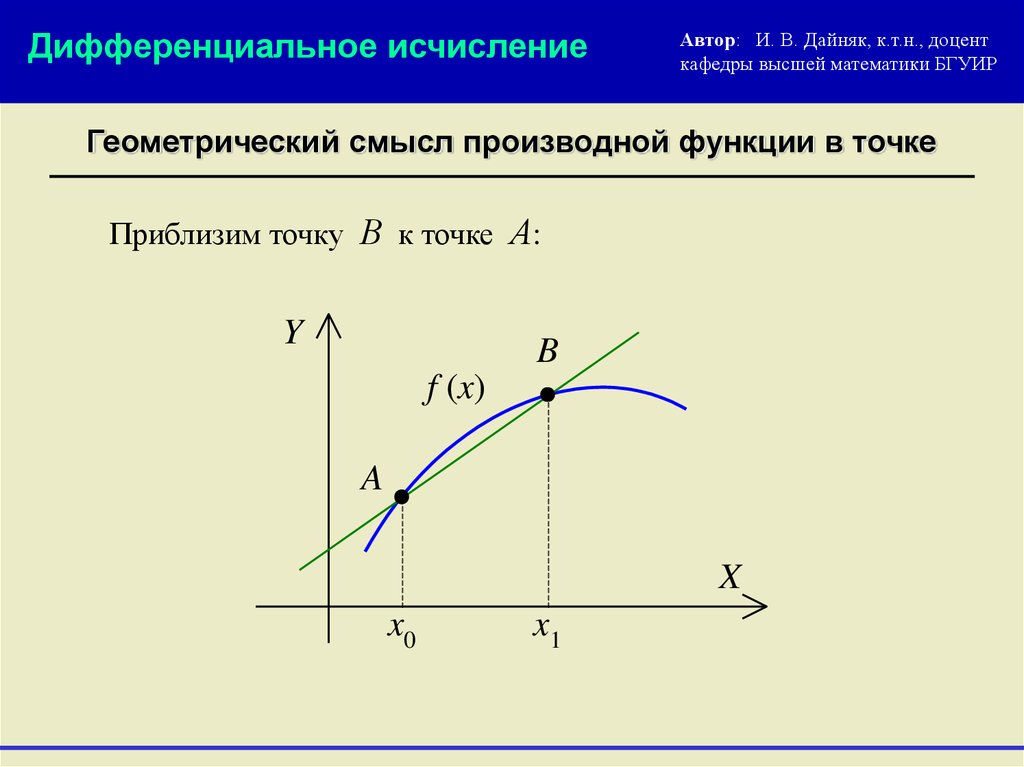
Геометрический смысл производной функции в точке
Приблизим точку В к точке А:
Y
B
f (x)
A
X
x0
x1

10.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
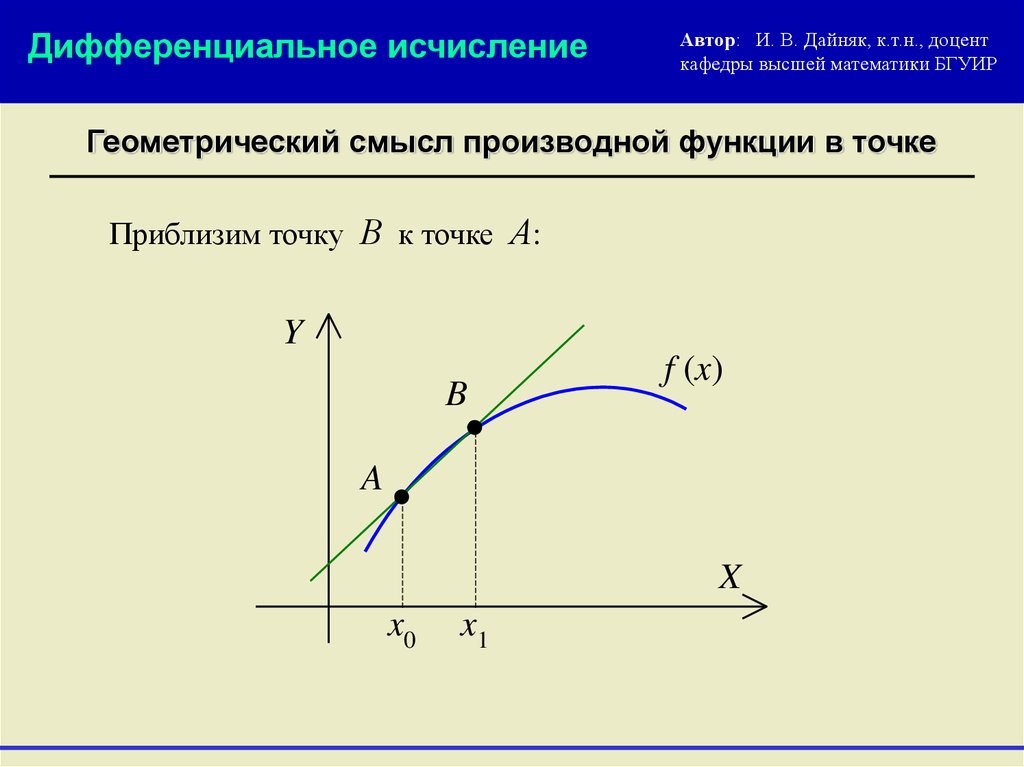
Геометрический смысл производной функции в точке
Приблизим точку В к точке А:
Y
B
f (x)
A
X
x0
x1

11.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Геометрический смысл производной функции в точке
Приблизим точку В к точке А:
Y
f (x)
A
X
x0

12.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
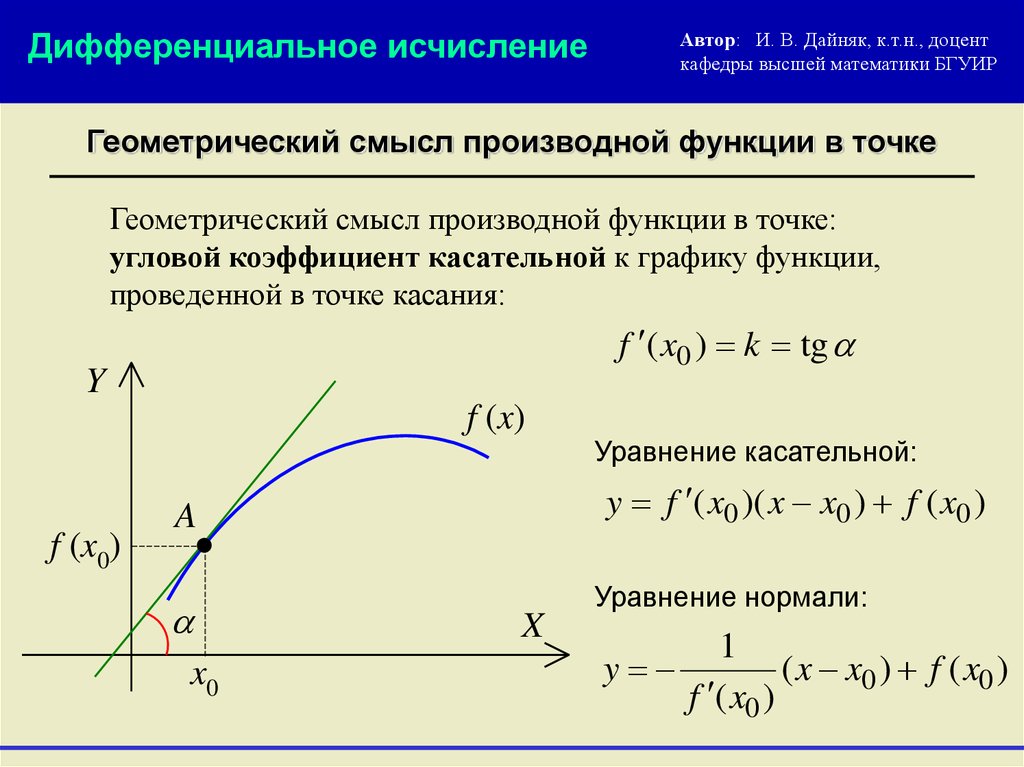
Геометрический смысл производной функции в точке
Геометрический смысл производной функции в точке:
угловой коэффициент касательной к графику функции,
проведенной в точке касания:
f ( x0 ) k tg
Y
f (x)
f (x0)
y f ( x0 )( x x0 ) f ( x0 )
A
x0
Уравнение касательной:
X
Уравнение нормали:
1
y
( x x0 ) f ( x0 )
f ( x0 )

13.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Физический смысл производной функции в точке
1. Пусть материальная точка М движется прямолинейно,
и функция s(t) есть пройденный ею путь за время t.
Пусть t0 – момент начала движения.
s (t ) s (t0 )
– средняя скорость движения.
Тогда отношение
t t0
s(t ) s(t0 )
Предел lim
s (t0 ) – мгновенная скорость
t t0
t t0
точки в момент t0.

14.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Физический смысл производной функции в точке
2. Пусть q (t0) – количество электричества, протекающего через
поперечное сечение проводника в момент времени t0.
Пусть t – промежуток времени.
Тогда
q q(t0 t ) q(t0 ).
q
Отношение
– средняя сила тока за время t.
t
q
Предел lim
q (t0 ) – мгновенный ток.
t 0 t

15.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производная функции в точке
Теорема 1: Основные формулы дифференцирования
Пусть функции u = u(x) и v = v(x) имеют производную
в точке x = x0. Тогда функции
c u, u v, u v, u
v
тоже имеют производные в точке x = x0, вычисляемые по
формулам:
1)
(c u ) c u
константу можно выносить за знак производной

16.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производная функции в точке
Теорема 1: Основные формулы дифференцирования
2) формула производной суммы
(u v) u v
3) формула производной произведения
(u v) u v u v
4) формула производной частного
u
u v u v
v
v2
(v( x) 0)

17.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производная функции в точке
Теорема 2: Дифференцирование сложной функции
Пусть функция g(x) имеет производную в точке x0, а
функция f (y) имеет производную в точке y0 = g(x0). Тогда
сложная функция f (g(x)) имеет производную в точке x0,
вычисляемую по формуле
f ( x0 ) f ( y0 ) g ( x0 ), y g ( x)
или
df df dg
f g g x
dx dg dx

18.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производная функции на отрезке
Если функция f (x) имеет производную в любой точке
некоторого интервала [a, b], то её производная на этом
интервале может быть выражена в виде некоторой
функции g(x) = f ’(x), которая находится по основным
формулам дифференцирования (теорема 1) и правилу
нахождения производной сложной функции (теорема 2).

19.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производные элементарных функций
1. Постоянная функция
f (x) = c, где с – константа.
f ( x) lim
x 0
f ( x x) f ( x)
c c
lim
0
x
x 0 x

20.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производные элементарных функций
2. Показательная функция
f ( x) a x , a 0, a 1
x x
x
a
a
(a x ) lim
x
x 0
x
a x (a x 1)
a
1
x
lim
a lim
a x ln a
x
x 0
x 0 x
Отсюда заключаем:
(e x ) e x .

21.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производные элементарных функций
3. Степенная функция
f ( x) x , R
(
x
x
)
x
( x ) lim
x
x 0
x
1
1
x
x lim
x x 1
x
x
x 0
1
При
2
имеем:
x
1/ 2
1 1 / 2
1
x x
.
2
2 x

22.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производные элементарных функций
4. Логарифмическая функция
f ( x) log a x, a 0, a 1,
x 0
log a ( x x) log a x
(log a x) lim
x
x 0
x
log a 1
x 1
lim
log a e
x
x
x 0
1
Отсюда следует, что (ln x) .
x
1
Кроме того, ln | x | .
x

23.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производные элементарных функций
5. Тригонометрические функции
Синус: sin x
sin( x x) sin( x)
x
x 0
(sin x) lim
lim
x 0
2 cos x x 2
2 sin x
x
lim cos x x
x 0
2 cos x

24.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производные элементарных функций
5. Тригонометрические функции
Косинус: cos x
cos(x x) cos(x)
(cos x) lim
x
x 0
2 sin x x sin x
sin x x
2
2 2 lim
2 sin x
lim
x
2
x 0
x 0

25.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производные элементарных функций
5. Тригонометрические функции
Тангенс: tg x
sin x
cos x
Производная находится по формуле производной частного:
sin x cos x cos x sin x ( sin x)
(tg x)
2
cos x
cos x
cos2 x sin 2 x
2
cos x
1
cos2 x

26.

Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производные элементарных функций
5. Тригонометрические функции
Тангенс: ctg x
cos x
sin x
Производная находится по формуле производной частного:
cos x ( sin x) sin x cos x cos x
(ctg x)
2
sin x
sin x
(sin 2 x cos2 )
sin 2 x
1
sin 2 x

27.

Высшая математика
Автор: И.В.Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
math.mmts-it.org