Похожие презентации:
Теория функций двух и нескольких переменных (ТФНП)
1.
Лекция 1Теория функций двух и
нескольких переменных (ТФНП).
1. Понятие ФНП.
2. Предел ФНП.
3. Непрерывность ФНП.
4. Частные производные первого порядка.
5. Производная сложной функции.
6. Производная неявной функции.
7. Производные высших порядков.
2.
1. Понятие ФНП.Пусть множество D – область на плоскости.
P( x, y ) D
Определение.
Если P D поставлено в соответствие
число f (P ) , то говорят, что на множестве
D задана числовая функция
z f ( P)
D – область определения функции.
3.
Если точка P ( x, y )задается двумя координатами,
то отображение ( x, y ) z
функция 2-х переменных
z f ( x, y ).
Графиком такой функции будет множество точек с
координатами x,y,z - поверхность в пространстве.
4.
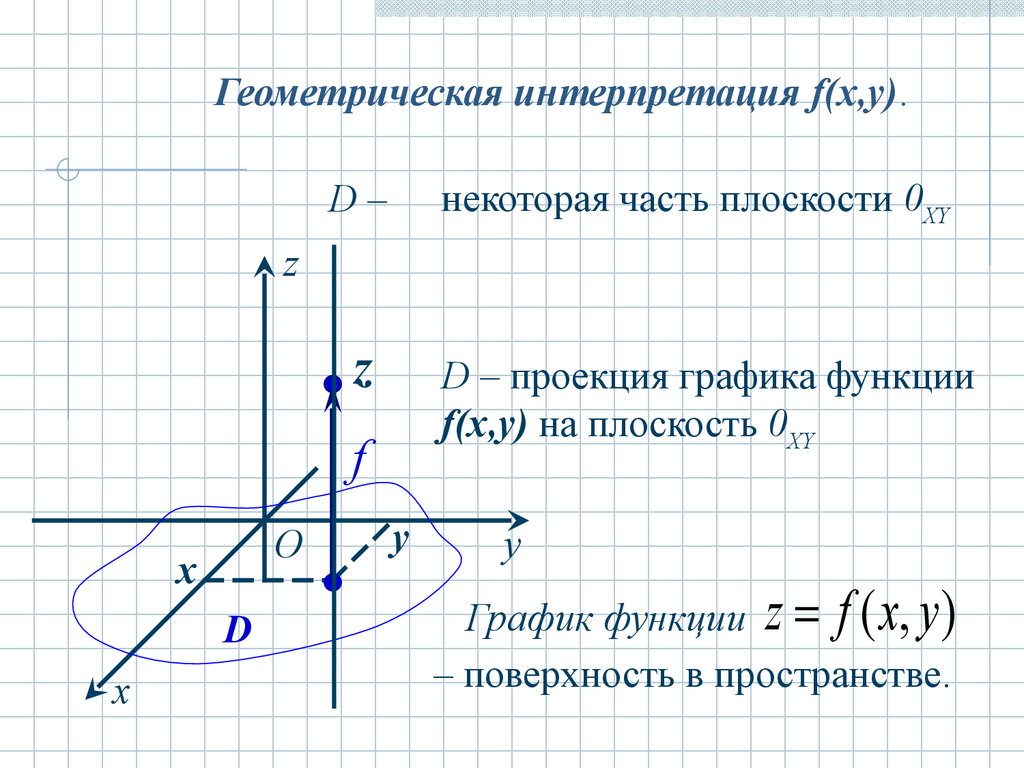
Геометрическая интерпретация f(x,y).некоторая часть плоскости 0ХY
D–
z
z
D – проекция графика функции
f(x,y) на плоскость 0ХY
f
О
x
D
x
y
y
График функции z f ( x, y )
– поверхность в пространстве.
5.
Пример 1.2
2
z R x y
– функция двух переменных
Область определения:
2
2
2
R x y 0
D:
2
2
x y R
Область значений:
E:
0 z R
2
(R – const )
y
R
2
x
6.
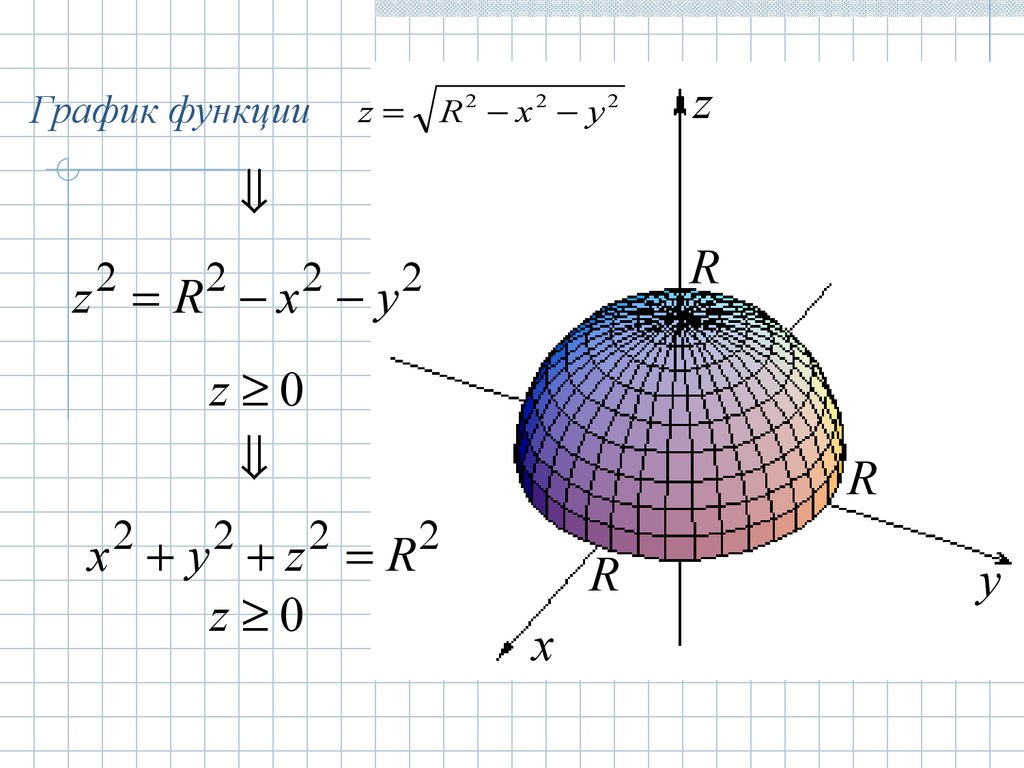
График функцииz
R2 x2 y2
z
2
2
2
z R x y
R
2
z 0
2
2
R
2
x y z R
z 0
2
R
x
y
7.
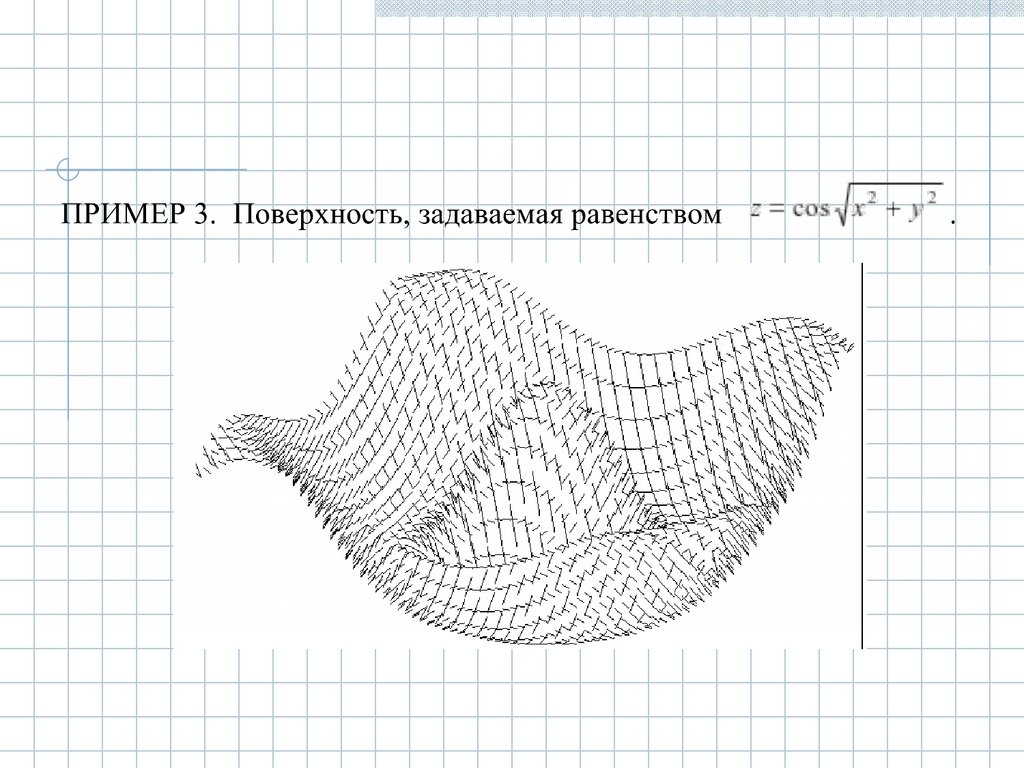
8.
9.
2.Предел функции двух переменных.
Пусть точка P0 D,
Множество точек
0 ( R )
P таких,
D,
что
P0 , P
называется - окрестностью точки P0 .
U P0 , P | P0 , P
y
P0
x
10.
Определение.Пусть точка P D.
Если 0 :
U P, D, то точка P
называется внутренней точкой множества D.
Определение.
Если все точки D внутренние для этого множества,
то оно называется открытым.
Определение.
Всякое открытое множество, содержащее точку
называется её окрестностью.
11.
Определение.Множество D любые две точки которого можно
связать непрерывной кривой, лежащей в этом
множестве , называется связным.
Определение.
Открытое связное множество называется областью.
12.
Пусть функция z f ( P ) определена в некоторойокрестности точки P (не обязательно в самой точке P
0
0
).
Число А называется пределом функции z f ( P )
при стремлении
P ( x, y ) P0 ( x0 , y0 ), если
0 ( ) 0 : 0 ( P, P0 ) f ( P) A
( P, P0 )
x x0
2
y y0
2
13.
Обозначение.A lim f ( P ) xlim
f
(
x
,
y
)
x
P P0
0
y y0
Замечание.
Стремление P P0 может происходить по
любому закону и направлению, при этом все
предельные значения существуют и равны А.
14.
Пример.Рассмотрим функцию
D : R / 0,0
f ( x, y )
2
lim f ( x, y ) lim
x 0
y 0
x2 2 y2
2
3x y
2
x2 2 y 2
x 0 3 x 2 y 2
y 0
Рассмотрим стремление P P0 по прямым,
проходящим через т. (0,0): y kx, x 0
lim
x 2 2 (kx) 2
1 2k 2
A
2
x 0 3 x 2 ( kx) 2
3 k
A A k значение А зависит от того как P P .
0
k R
предел не существует.
15.
3.Непрерывность ФНП.
Функция u f (P )
называется
непрерывной в точке P0 , если
1) f ( P0 )
2) lim f ( P ),
P P0
3) lim f ( P ) f ( P0 ).
P P0
Если хотя бы одно из условий 1-3 нарушено, то
P0 - точка разрыва .
16.
Точки разрыва могут быть изолированными,образовывать линии разрыва, поверхности разрыва.
Пример.
а)
б)
z
z
2
1
2
2
x y
1
2
Точка разрыва – P0 0,0
(изолированная)
2
x y 4
2
x y 4 - линия разрыва
17.
4.Частные производные первого порядка.
Пусть
z f ( x, y )
определена в области D.
Определение.
Разность x z f ( x x, y ) f ( x, y )
называется частным приращением функции
по переменной x.
Здесь ( x, y ) – внутренняя точка
точка
( x x, y ) D f
D( f )
18.
Разность y z f ( x, y y ) f ( x, y )называется частным приращением функции
по переменной y .
Здесь ( x, y ) – внутренняя точка D( f ),
точка ( x, y y ) D f .
19.
Определение.Разность
z f ( x x, y y ) f ( x, y )
называется полным приращением функции.
Определение.
Пределы
yz
x z
z
z
lim
, lim
x 0 x
x y 0 y
y
называются частными производными
функции (при условии, что они существуют).
20.
Обозначение.z
x
z
x f x ( x, y )
z
f ( x x, y ) f ( x, y )
lim
x x 0
x
21.
Правила вычисления частных производныхФНП совпадают с соответствующими правилами
для функции одной переменной.
Замечание.
При вычислении производной ФНП по одной из
переменных все остальные рассматриваются
как постоянные.
Пример.
u x2 y
u 1
2x
;
x 2 x 2 y
u 1
1
y 2 x 2 y
22.
Определение.Главная (линейная) часть полного приращения
функции в точке называется полным
дифференциалом функции в этой точке.
23.
Пример:Если
u ( x, y ) xy,
Vu u x Vx, y Vy u ( x, y )
x Vx y Vy xy xVy yVx VxVy
du dxdy,
где Vx dx, Vy dy
24.
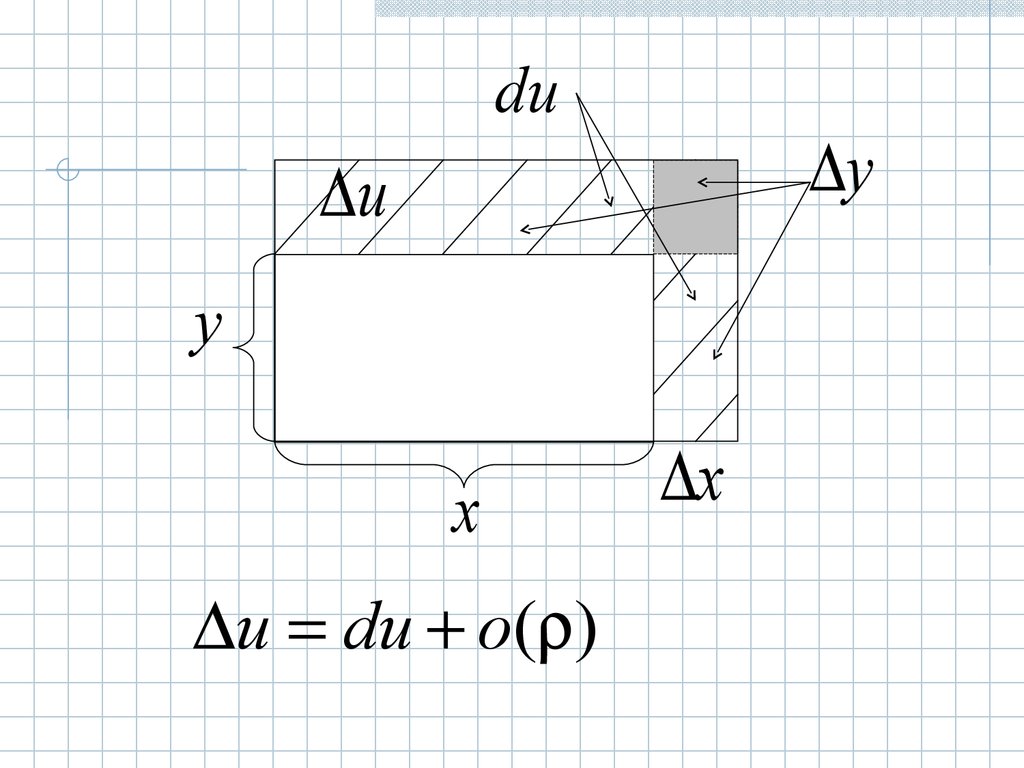
duy
u
y
x
u du o( )
x
25.
Дифференциал функции двух переменныхu
u
du ( x, y ) dx dy
x
y
26.
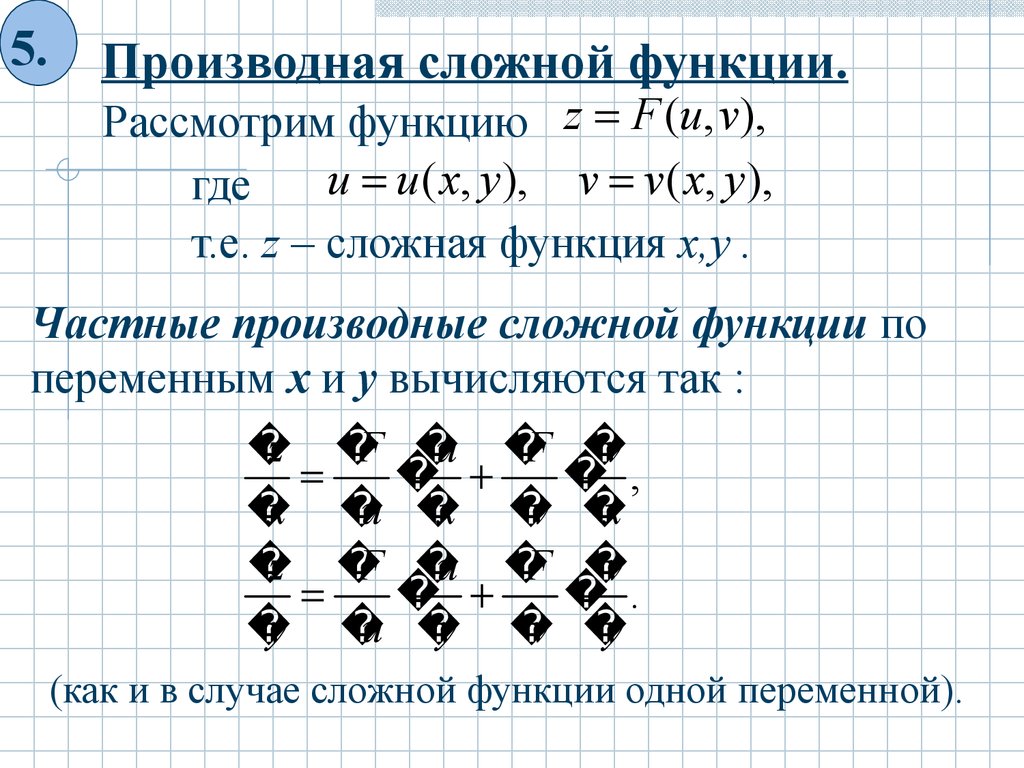
5.Производная сложной функции.
Рассмотрим функцию z F (u, v),
u u ( x, y ), v v( x, y ),
где
т.е. z – сложная функция x,y .
Частные производные сложной функции по
переменным x и y вычисляются так :
z
F
u
F
v
,
x
u
x
v
x
z
F
u
F
v
.
y
u
y
v
y
(как и в случае сложной функции одной переменной).
27.
Полная производнаяа) z F ( x, y ), где x x(t ),
y y (t ),
т.е. z – сложная функция одного аргумента t.
Тогда
dz
F dx
F dy
dt
x dt
y dt
- полная производная функции по аргументу t.
28.
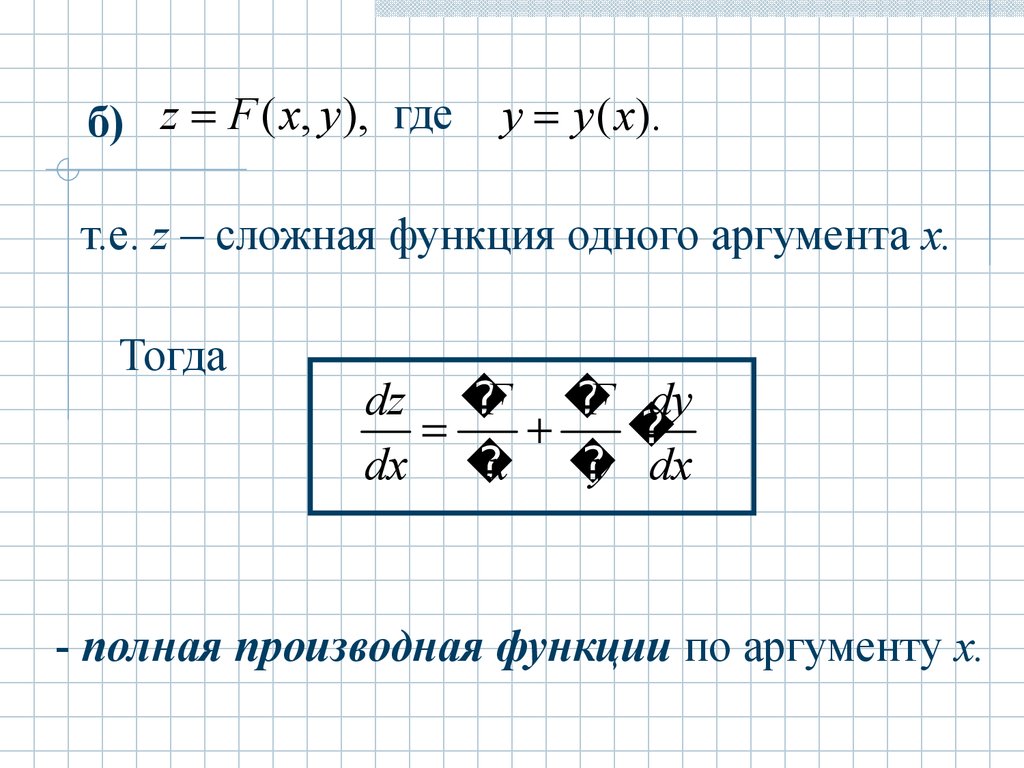
б) z F ( x, y ), гдеy y ( x).
т.е. z – сложная функция одного аргумента x.
Тогда
dz
F
F dy
dx
x
y dx
- полная производная функции по аргументу x.
29.
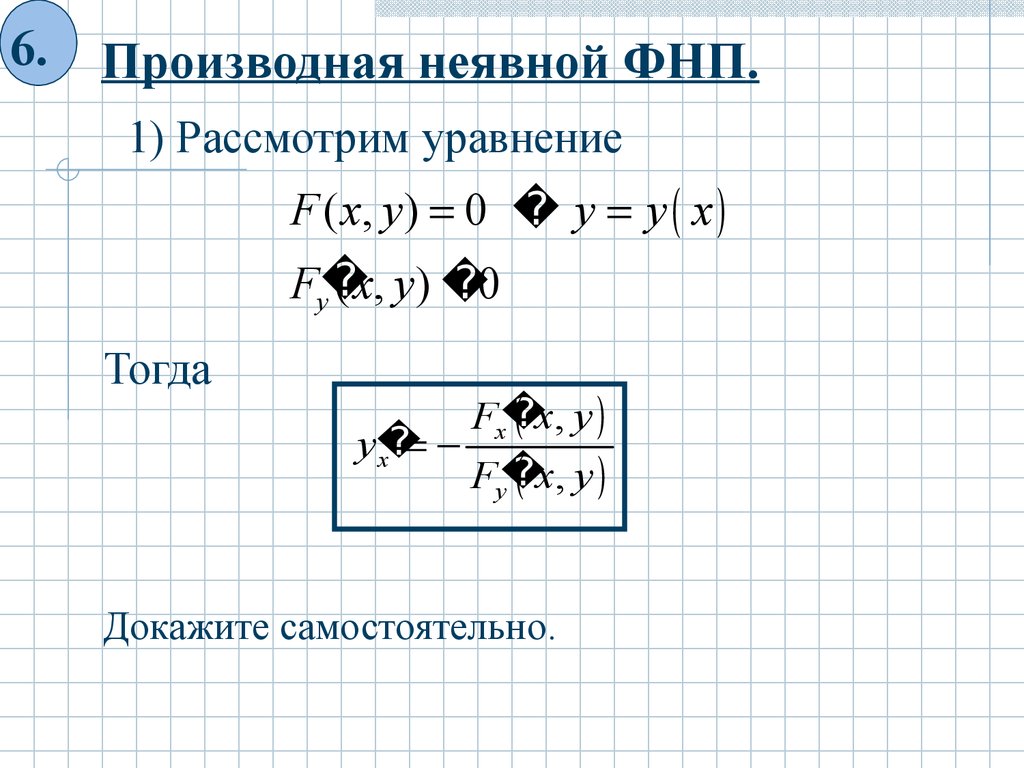
6.Производная неявной ФНП.
1) Рассмотрим уравнение
F ( x, y ) 0 y y x
Fy
( x, y ) 0
Тогда
Fx
x, y
y
x
Fy
x, y
Докажите самостоятельно.
30.
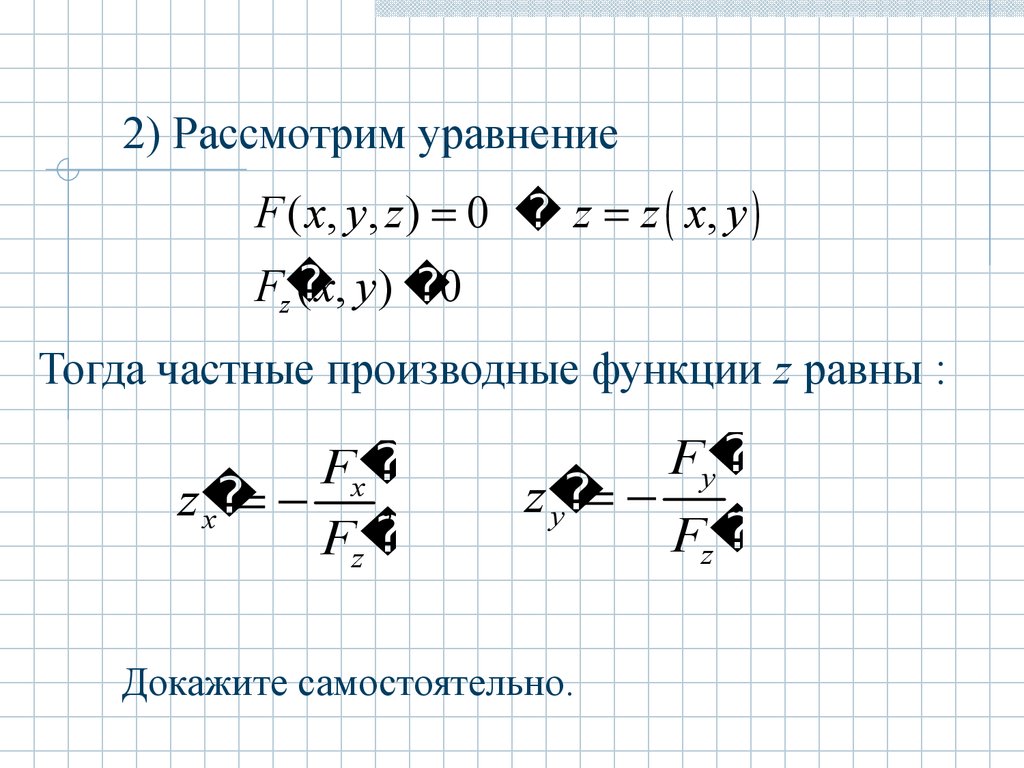
2) Рассмотрим уравнениеF ( x, y , z ) 0 z z x, y
Fz
( x, y ) 0
Тогда частные производные функции z равны :
Fx
z
,
x
Fz
Fy
z
.
y
Fz
Докажите самостоятельно.
31.
7.Производные высших порядков.
Для функции z f ( x, y ), частные производные
z
z
f x ,
f y ,
x
y
также являются функциями двух переменных,
которые тоже можно дифференцировать:
2
z
z 2 z
z
f xx ,
f
yy
x x y 2
y y
x 2
- частные производные второго порядка
2
z
z
z
z
f yx
f xy
,
x y
x
y
y x
y
x
- смешанные частные производные второго порядка.
2
32.
ТеоремаЕсли
(о равенстве смешанных производных).
f xy и f yx
непрерывны, то
f yx
.
f xy
33.
Все изложенное для функций двух переменныхможет быть обобщено для функций n
переменных.



















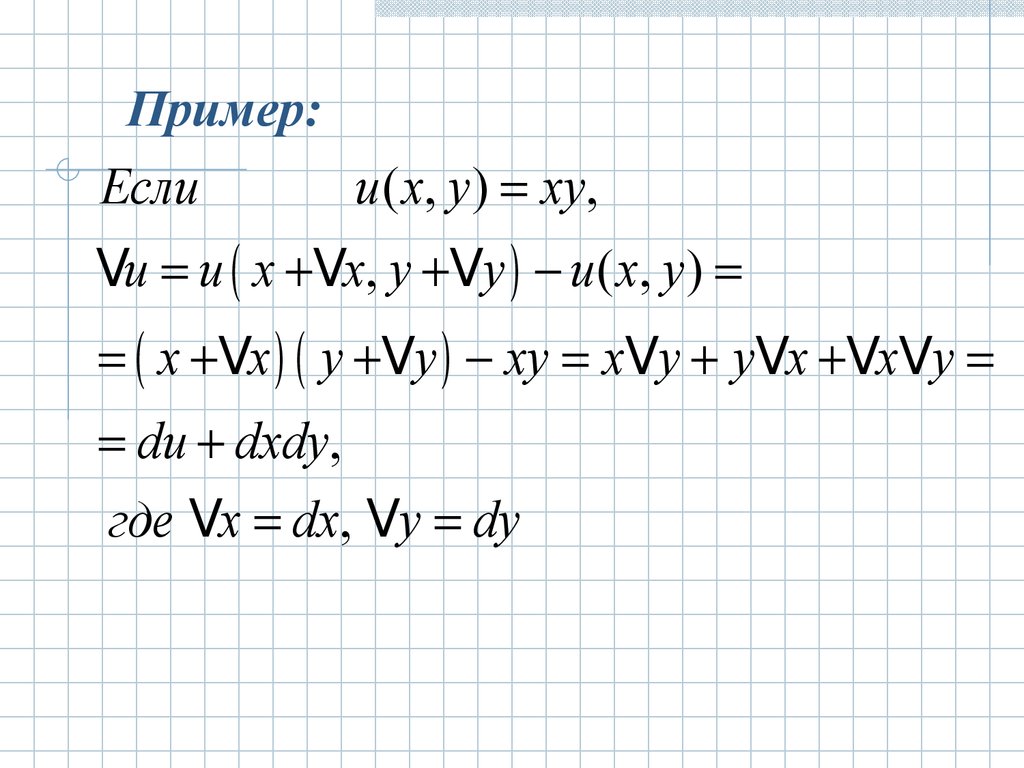





 Математика
Математика








