Похожие презентации:
Функции
1. Функции
Её значение определяется областьюопределения;
Она отражает связь между
элементами множеств, она бывает
Их используют
во всех
графической,практически
аналитической,
областях
геометрии,тригонометрической,
физики и инженерного
геометрической,
алгебраической;
дела…
Её можно отображать тождественно,
композиционно, обратно-заданной;
Она – неотъемлемая часть
программирования…
ЯрошКорпорейшен
и
и
ц
ДАЛЕЕ
к
н
представляет
у
Ф
2.
Функция (отображение, оператор,преобразование) — математическое
понятие, отражающее связь между
элементами множеств.
Термин
Термин «функция»
«функция» (в
(в некотором
некотором более
более узком
узком смысле)
смысле) был
был
впервые
впервые использован
использован Лейбницем
Лейбницем (1692
(1692 год).
год). В
В свою
свою очередь,
очередь,
Иоганн
Иоганн Бернулли
Бернулли вв письме
письме к
к тому
тому же
же Лейбницу
Лейбницу употребил
употребил этот
этот
термин
термин вв смысле,
смысле, более
более близком
близком к
к современному.
современному.
Первоначально,
Первоначально, понятие
понятие функции
функции было
было неотличимо
неотличимо от
от понятия
понятия
аналитического
аналитического представления.
представления. Впоследствии
Впоследствии появилось
появилось
определение
определение функции,
функции, данное
данное Эйлером
Эйлером (1751
(1751 год),
год), затем
затем —
—у
у
Лакруа
Лакруа (1806
(1806 год)
год) —
— уже
уже практически
практически вв современном
современном виде.
виде.
Наконец,
Наконец, общее
общее определение
определение функции
функции (в
(в современной
современной форме,
форме,
но
но для
для числовых
числовых функций)
функций) было
было дано
дано Лобачевским
Лобачевским (1834
(1834 год)
год)
и
и Дирихле
Дирихле (1837
(1837 год).
год).
К
К концу
концу XIX
XIX века
века понятие
понятие функции
функции переросло
переросло рамки
рамки числовых
числовых
систем.
систем. Первыми
Первыми это
это сделали
сделали векторные
векторные функции,
функции, вскоре
вскоре
Фреге
Фреге ввёл
ввёл логические
логические функции
функции (1879),
(1879), а
а после
после появления
появления
теории
теории множеств
множеств Дедекинд
Дедекинд (1887)
(1887) и
и Пеано
Пеано (1911)
(1911)
сформулировали
сформулировали современное
современное универсальное
универсальное определение.
определение.
ДАЛЕ
3.
АНАЛИТИЧЕСКИЙСПОСОБ ЗАДАНИЯ
ФУНКЦИИ:
Если ввести переменную x, пробегающую
множество X и переменную y, пробегающую
множество Y, то функцию можно задать
аналитически, как: y=f(x).
Например: y=, где х пробегает множество
вещественных чисел, задаёт некоторую
функцию f. Важно понимать, что само
выражение не является функцией. Функция,
как объект, представляет собой множество
(упорядоченных пар). А данное выражение,
как объект, есть равенство двух переменных.
Оно задаёт функцию, но не является ею.
Однако, во многих разделах математики,
можно обозначать через f(x) как саму
функцию, так и аналитическое выражение,
ДАЛЕее
4.
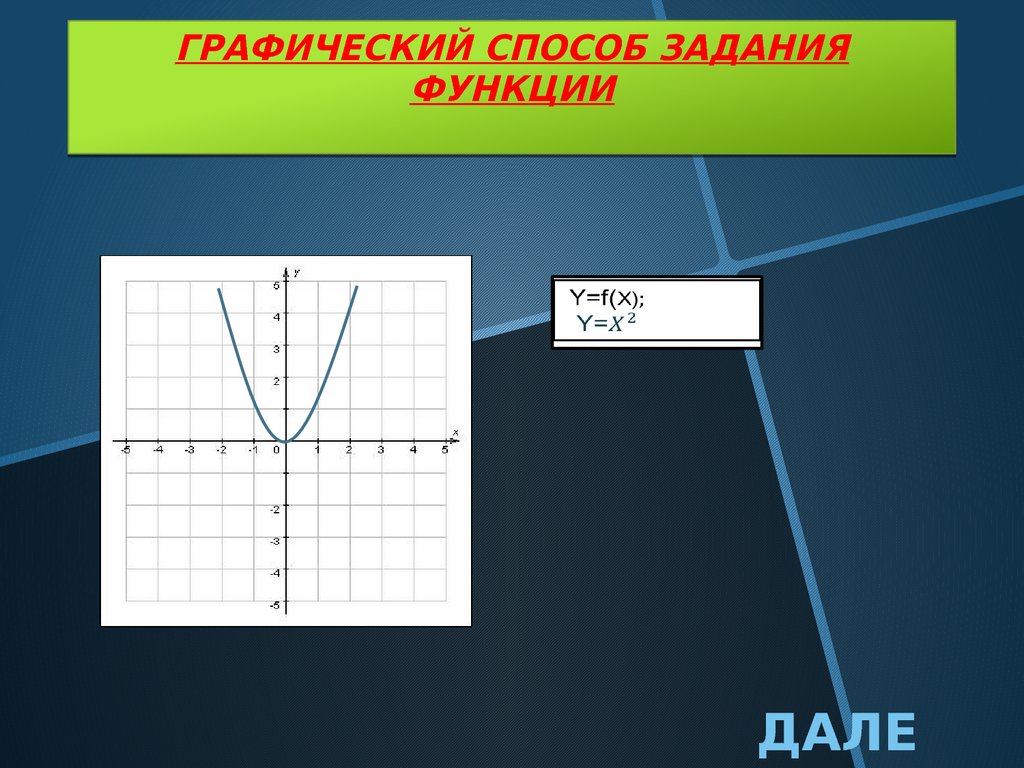
ГРАФИЧЕСКИЙ СПОСОБ ЗАДАНИЯФУНКЦИИ
Y=f(X);
Y=
ДАЛЕ
5.
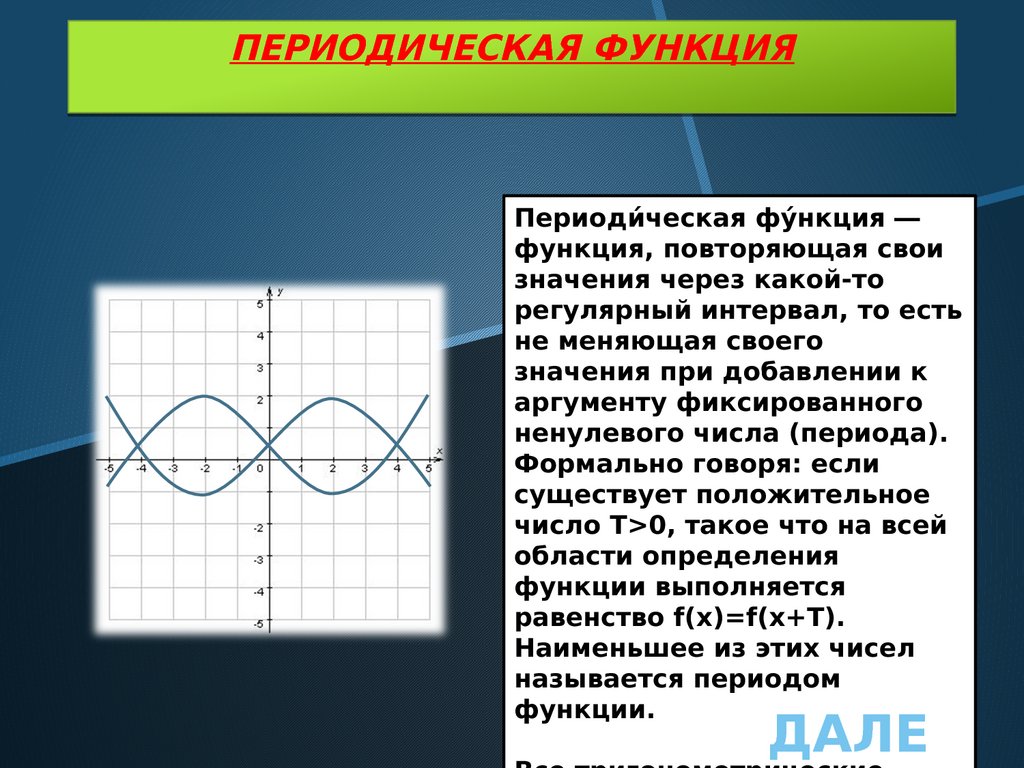
ПЕРИОДИЧЕСКАЯ ФУНКЦИЯПериодии́ ческая фуи́ нкция ―
функция, повторяющая свои
значения через какой-то
регулярный интервал, то есть
не меняющая своего
значения при добавлении к
аргументу фиксированного
ненулевого числа (периода).
Формально говоря: если
существует положительное
число T>0, такое что на всей
области определения
функции выполняется
равенство f(x)=f(x+T).
Наименьшее из этих чисел
называется периодом
функции.
ДАЛЕ
6.
НЕЧЁТНЫЕ И ЧЁТНЫЕ ФУНКЦИИF(x)=x
F(x)= ––ни
пример
пример
F(x)=+1
чётная,
нечётной
чётной
функции
функции
ни
нечётная
функция
Нечётными и чётными
называются функции, графики
которых обладают
симметрией относительно
изменения знака аргумента.
Нечётная функция — функция,
меняющая знак при изменении
знака независимого переменного
(симметричная относительно
центра координат).
Чётная функция — функция, не
изменяющая своего значения при
изменении знака независимого
переменного (симметричная
относительно оси ординат).
Индифферентная функция—
функция, не обладающая
симметрией. В эту категорию
относят функции не подлежащие
для предыдущих 2 категорий.
7.
МОНОТОННОСТЬ ФУНКЦИИМонотонная функция — это
функция, меняющаяся в одном и
том же направлении.
Если в дополнение приращение
не равно нулю, то функция
называется строго
монотонной.
Функция возрастает, если
большему значению аргумента
соответствует большее
значение функции. Функция
убывает, если большему
значению аргумента
соответствует меньшее
значение функции.
ДАЛЕ
8.
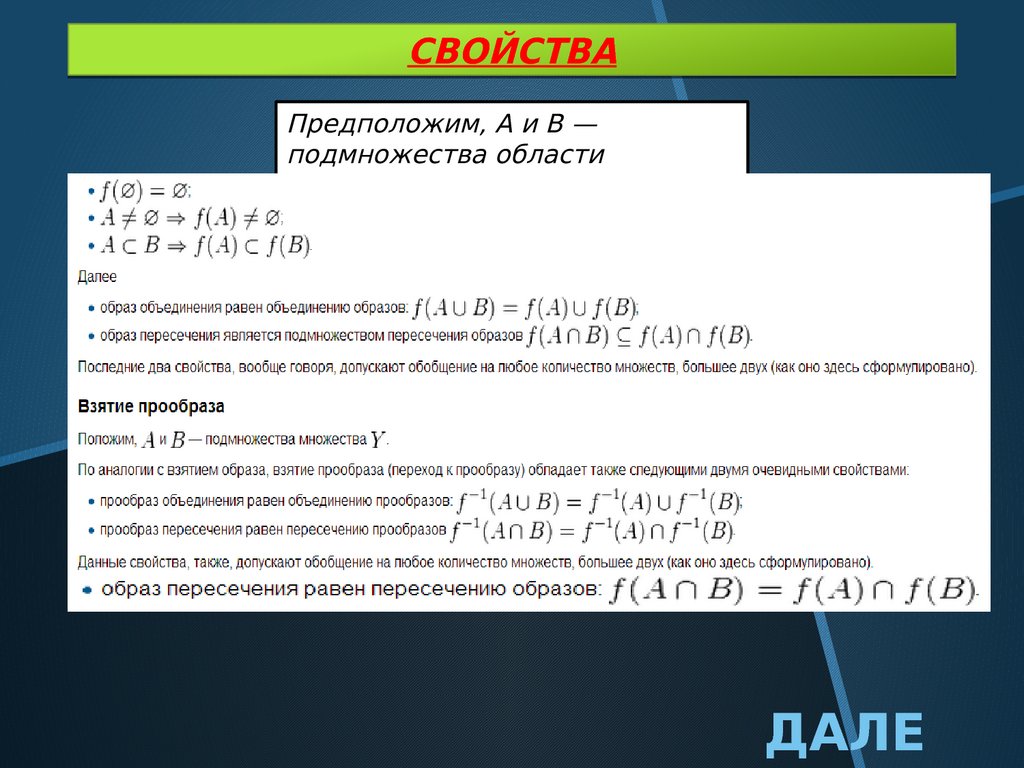
СВОЙСТВАПредположим, A и B —
подмножества области
определения.
ДАЛЕ
9.
КонецПроект готовил Михаил
Ярошенко






 Математика
Математика








