Прямая задача теории погрешности. Лекция 3

1.

Тема: Прямая задача теории погрешности
Суть - оценивание погрешности произвольной функции нескольких переменных
через заданные погрешности аргументов.
Пусть u=f(x1,x2,…,xn) – дифференцируемая функция,
Δxi - погрешности аргументов.
Тогда абсолютная погрешность функции
u f x1 x1, x2 x2 , , xn xn f x1 , x2 , xn
Тогда можно записать:
n
f
f
u df x1 , x2 , , xn
xi
xi
i 1 xi
i 1 xi
n
(1)
Отсюда для предельной абсолютной погрешности функции получаем:
n
u
u
xi
i 1 xi
Оценка относительной погрешности u : // обе части неравенства (1) делим на u
f
n
n
xi
xi
ln f x1 , , xn xi
i 1 u
i 1 xi
Следовательно, предельная
относительная погрешность функции u:
n
u
i 1
ln u xi
xi

2.

Прямая задача теории погрешности. Пример.
Найти предельную абсолютную и относительную погрешности объёма шара
1
V d 3
6
, если диаметр d = 3,7 см ±0,05 см, а π 3,14.

3.

Обратная задача теории погрешности
Суть - оценивание погрешностей аргументов произвольной функции нескольких
переменных, обеспечивающих заданную или меньшую погрешность функции.
В такой постановке задача некорректна, так как допускает множество разных
решений. Нужны дополнительные предположения.
Принцип равных влияний. Все частные дифференциалы
f
xi
xi
i 1, 2, ..., n
вносят одинаковый вклад в образование общей абсолютной погрешности
функции.
Пусть величина абсолютной погрешности функции Δu задана. Воспользуемся
формулой предыдущего раздела:
n
u
i 1
u
x
xi
i
Согласно принципу равных влияний:
u
u
u
xi
x2 ...
xn u
x1
x2
xn
n
Отсюда получаем:
xi
u
u
n
xi
(2)

4.

Обратная задача теории погрешности. Пример.

5.

Тема: Вычисление значений функций
2. Вычисление значения алгебраического полинома.
Схема Горнера.
Рассмотрим полином
P( x) an x n an 1 x n 1 ... a1 x a0
Наша задача – найти значение этого полинома при x = ξ. То есть
вычислить P( ) an n an 1 n 1 ... a1 a0
Для рационального вычисление перепишем P( ) в виде
P an an 1 an 2 .... a2 a1 a0
Отсюда легко сконструировать нужную последовательность
вычислений, начиная с самых внутренних скобок:
b0=an;
b1=an-1+b0ξ;
b2=an-2+b1ξ;
………
bn-1=a1+bn-2ξ;
bn=a0+bn-1ξ.
это искомое значение: bn P .

6.

Вычисление значений функций. Схема Горнера.
Сравним эффективность предложенного варианта вычислений (схемы
Горнера) с прямым вычислением «в лоб». В качестве критерия будем
использовать количество операций умножения.
При вычислении по формуле нам потребуется выполнить
1+2+3+…+n=n(n+1)/2 операций умножения. А по схеме Горнера только
n операций.

7.

Тема: Вычисление значений функций
Покажем, что числа b0 , b1 , , bn 1 являются коэффициентами полинома Q(x),
полученного в качестве частного при делении данного полинома P(x)
на двучлен x - .
Q x 0 x n 1 1 x n 2 n 1
P x 0 x n 1 1 x n 2 n 1 x n
P x 0 x n 1 0 x n 1 2 1 x n 2 n 1 n 2 x n n 1
P( x) an x n
an 1 x n 1
0 an ,
1 0 a n 1 ,
2 1 a n 2 ,
n 1 n 2 a1 ,
n n 1 a0 .
an 2 x n 2 .... .... ... .. .... .. .... a1 x
0 an b0 ,
1 an 1 0 b1
2 an 2 1 b2 ,
n 1 a1 n 2 bn 1 ,
n a0 n 1 bn ,
a0
b0 a n ,
b1 a n 1 b 0 ,
b 2 a n 2 b1 ,
b3 a n 3 b 2 ,
b n 1 a1 b n 2 ,
b n a 0 b n 1 ,

8.

Вычисление значений функций.
2. Приближенное суммирование числовых рядов
Определение. Числовой ряд
a1 a2 an
называется сходящимся, если существует предел последовательности его
частных сумм S lim S n , где S n a1 a2 an .
n
Задача. Найти сумму S сходящегося числового ряда
точностью ε (ε – абсолютная погрешность).
a
i 1
i
с нужной
Решение. Сумма сходящегося ряда всегда представляется в виде:
S S n Rn ,
где Sn – n-ая частичная сумма,
R 0
n
Rn – остаток ряда, причем
при
n
.
Остаток ряда характеризует остаточную погрешность.
Источники погрешности при суммировании сходящегося ряда:
1.остаточная погрешность,
2. погрешность вычисления самих элементов ряда,
3. погрешность при округлении результата.

9.

Вычисление значений функций.
2. Приближенное суммирование числовых рядов
Процедура вычислений.
Выбираем три положительных числа ε1, ε2, ε3, таких, что
1 2 3
1) остаточная погрешность (ε1) :
Количество ‘n’ слагаемых в частичной сумме Sn выберем столь
большим, чтобы остаточная погрешность
Rn 1
2) погрешность вычисления самих элементов ряда (ε2) :
Каждое из слагаемых ai частичной суммы вычисляем с предельной
2
абсолютной погрешностью, не превышающей
и пусть a k n
соответствующие приближенные значения членов ряда, и выполняется:
ak ak
2
n

10.

Тогда для частичной суммы
n
S n ak
k 1
погрешность действий (суммирования) удовлетворяет неравенству
Sn Sn 2
3) Погрешность при округлении результата (ε3) .
Результат S n округлим до S n так, чтобы для погрешности округления
результата выполнялось соотношение:
Sn Sn 3
При выполнении такой процедуры суммирования ряда, полученный результат
будет соответствовать искомой сумме с погрешностью не более ε.
В самом деле,
S S n S S n S S n S n S n 1 2 3 .
Разбиение числа на положительные слагаемые
производят следующим образом:
1 , 2 , 3
4
4
2
1 , 2 , чаще
3
всего

11.

Теорема 1. Если члены ряда представляют собой соответствующие
значения положительной монотонно убывающей функции f(x), то есть
a n f ( n)
n 1, 2, , тогда
f ( x)dx Rn
n 1
f x dx
n
Теорема 2. Если ряд знакочередующийся и модули его членов монотонно
убывают, тогда
Rn a n 1

12.

Вычисление значений функций.
2. Приближенное суммирование числовых рядов
Пример.
1 1 1
1
...
... с точностью 0,004.
3
3
3
3
1 2 3
n
Решение. Округлять результат и слагаемые не будем 2 3 0.
Найти сумму ряда
S
Тогда погрешность вычисления суммы равна остаточной погрешности:
1 0,004
Члены ряда представляют собой значения монотонно убывающей
1
функции
f x 3
x
Поэтому для n-го остатка ряда имеем оценку (по теореме 1):
Rn
Решая неравенство:
Получим
dx
1
n x3 2n2
1
1
,
2
2n
4000
n 2000 44,7. Следовательно, n=45.

13.

Вычисление значений функций.
3. Вычисление значений аналитических функций
Функция f(x) аналитическая в точке x = ξ, если в окрестности этой точки
она разлагается в ряд Тейлора, то есть ее можно представить в виде (1)
( n)
f ( )
f
( )
f ( x) f ( ) f ( )( x )
( x ) 2 ...
( x ) n ...
2!
n!
Остаточный член разложения Rn(x) представляет собой ошибку при
замене функции отрезком ряда Тейлора:
n
Rn ( x) f ( x)
k 0
f ( k ) ( )
(x )k
k!
Для остаточного члена существует несколько форм представления. Одна
из них такая
f ( n 1) ( ( x ))
Rn ( x)
( x ) n 1 ,
(n 1)!
0 1

14.

Вычисление значений функций.
3. Вычисление значений аналитических функций
Если f(ξ) известно и требуется найти значение f(ξ + h), где h – «малая
поправка», то формулу (1) выгодно записать в виде:
f ( ) 2
f ( n) ( ) n
f ( h) f ( ) f ( ) h
h ...
h Rn h .
2!
n!
где
f ( n 1) ( x) n 1
Rn ( x)
h ,
(n 1)!
0 1.

15.

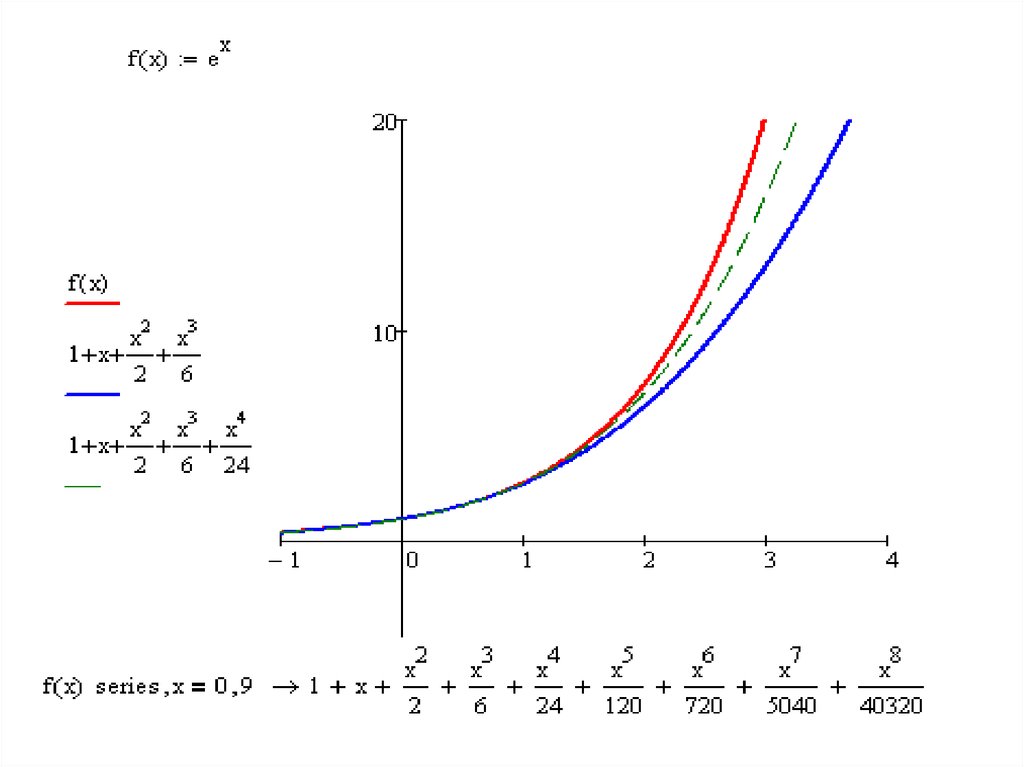
Вычисление экспоненты ( ех).
Известно из курса математического анализа, что экспоненциальная
функция в окрестности точки 0 разлагается в ряд Тейлора вида:
2
3
n
x
x
x
ex 1 x
...
...
2! 3!
n!
Остаточный член этого ряда имеет вид:
e x
Rn ( x)
x n 1 0 1.
( n 1)!
Непосредственно в таком виде использовать представление экспоненты
неэффективно, так как хn+1 сильно растет, когда |x|>1. Для достижения
требуемой точности придется использовать много членов разложения
(большая трудоемкость). Для обхода этих затруднений предлагается
следующая процедура.
Представим аргумент х в виде:
х = Е(х) + q,
Е(х) – целая часть числа х,
q – дробная часть (|q|<1). Тогда
e x e E x eq

16.

17.

Число е = 2.71828182… известно с очень высокой точностью. Поэтому
величину еЕ(х) = е*е*е*…*е можно считать вычисляемой с какой угодно
точностью. Второй сомножитель еq будем вычислять, пользуясь
разложением в ряд Тейлора. Очевидно, что при |q|<1 сходимость ряда
qn
e
n 0 n !
q
будет быстрой, то есть потребуется мало членов разложения.
Для величины остаточного члена можно получить более точную оценку. В
самом деле, по определению остатка, можем записать
q n 1
q n 2
q n 3
Rn (q)
...
(n 1) ! (n 2) ! (n 3) !
q n 1
1
q n 1
q
q2
[1
...]
(n 1) ! 1 q
(n 1) !
(n 2) (n 2)(n 3)
n 2

18.

Если учесть, что n 2 n 1 , то получим
n 1 n
Если обозначить
q n 1 n 1 q n 1
Rn (q)
(n 1) ! n n n !
qn
un
, un - последний сохраненный член частичной
n!
суммы, тогда для остаточного члена можно записать
q
0 Rn (q) u n
n
Если нам задана остаточная погрешность (εr), тогда количество
слагаемых частичной суммы ряда легко определить в процессе
вычисления. Находить новые слагаемые и суммировать их можно
прекратить, как только для очередного слагаемого выполниться
условие
q
un
r
n

19.

Таким образом вычисление экспоненциальной функции сводится
ех = u0 + u1 + u2 +…+ un, где u0 =1, uk = xuk-1/k .
Предложенный ранее вариант определения количества слагаемых
можно уточнить (дать более точные условия прекращения
суммирования) если предположить, что выполняются следующие
нежесткие условия, а именно: n≥ 2 |x| >0. В этом случае
Rn ( x) Rn ( x )
x
n 1
(n 1) !
1
1
x
n 2
С учетом принятого предположения, вторая дробь не может быть больше
2 Тогда,
Rn
2x
n 1
2x
x
n
u
(n 1) ! n 1 n !
Отсюда вывод, процесс суммирования можно прекратить, если последний
вычисленный член un по модулю не превосходит εr, то есть |un|< εr.
n
r