Похожие презентации:
Дифференцируемость функции нескольких переменных. Лекция 3
1.
Математика 2 семестр.Лекция 3.
Дифференцируемость функции
нескольких переменных.
2.
Дифференцируемость функции двух переменных.• Для функции одной переменной у = f(x) необходимым и достаточным
условием дифференцируемости её в точке х0, т.е. представление
приращения ∆y в виде суммы
∆y = f (х0)∆x+α∆x, где α→0 при ∆х→0,
является существование производной f (x) в точке х0.
• В случае же функции двух (или большего числа) переменных
дифференцируемость и существование частных производных не
являются эквивалентными свойствами функции.
• Пусть функция z=f(x;y) определена в некоторой окрестности точки
М(x;y). Зададим в этой точке приращения аргумента ∆x≠0 и ∆y≠0.
Полное приращение этой функции в точке М(x; y):
∆z = f(x+∆x; y+∆y) - f(x; y)
3.
Определение.Функция z=f(x; y) называется дифференцируемой в точке М(x; y),
если её полное приращение в этой точке можно представить в виде:
∆z = A∆x + B∆y + α∆x + β∆y,
где А и В не зависят от ∆x и ∆y, α=α(∆x; ∆y)→0 и β=β(∆x; ∆y)→0
при ∆x→0; ∆y→0. Сумма первых двух слагаемых в этом равенстве
представляет собой главную часть приращения функции.
4.
Теорема (необходимое условие дифференцируемостифункции).
Если функция z=f(x; y) дифференцируема в точке М(x; y), то
она непрерывна в этой точке и имеет в ней конечные
частные производные = A и = B.
Доказательство.
Так как функция дифференцируема в точке М(x; y), то имеет
место равенство ∆z = A ∆x + B ∆y + α ∆x + β ∆y.
По определению функция z=f(x;y) непрерывна, если
5.
В нашем случае= A ∆x + B ∆y + α ∆x + β ∆y=0,
а это означает, что функция z=f(x; y) непрерывна в точке М.
В равенстве ∆z = A∆x + B∆y + α∆x + β∆y положим ∆y=0 и
∆x≠0, получим, что частное приращение по x равно
∆хZ=A∆x+α∆x и =A+α. Переходя к пределу при ∆x→0,
имеем
Аналогично,
6.
1. Условие дифференцируемости можно записать в виде:∆z = ∆x + ∆y + α∆x + β∆y
2. Обратная теорема не верна, т.е. существование частных
производных
не
является
достаточным
условием
дифференцируемости функции z = f(x;y) в точке.
Теорема (достаточное условие дифференцируемости).
Если функция z=f(x;y) имеет непрерывные частные
производные f’x(x;y) и f’y(x;y) в точке M(x;y), то она
дифференцируема в этой точке.
7.
Полный дифференциал функции.•Пусть функция z=f(x;y) дифференцируема в точке M(x;y), т.е. её
приращение можно представить в виде:
∆z=[∆x + ∆y ]+(α∆x+β∆y), где α→0, β→0 при ∆x→0 и ∆y→0
Выражение в квадратных скобках является линейной относительно ∆x и
∆y частью приращения функции, а выражение в круглых скобках –
бесконечно малой функцией при ∆x→0 и ∆y→0.
Полным дифференциалом функции z=f(x; y) в точке M(x;y)
называется линейная функция аргументов ∆x и ∆y
dz = ∆x + ∆y
Дифференциалами независимых переменных x и y будем называть
приращение этих переменных: dx=∆x; dy=∆y. Тогда дифференциал
функции z=f(x; y) в точке M(x; y) можно записать в виде:
dz = dx + dy
8.
Полный дифференциал функции.•Аналогичное равенство при условии существования непрерывных
частных производных имеет место и для функции n переменных
U=f(x ,x ,…,xn)
1
2
Полный дифференциал
dU= dx1+ dx2+…+ dxn
Слагаемые dx и dy называются частными дифференциалами функции
z=f(x; y) по аргументам x и y.
Тогда dxz = dx и dyz = dy и полный дифференциал есть сумма частных
дифференциалов dz=dxz+dyz.
9.
Пример.Найти полный дифференциал функции z = .
Имеем
=
;
=-
,
тогда
dz = dx + dy =
dx -
dy =
;
10.
Частные производные высших порядков.•Пусть имеется функция u=f(x1,x2,…,xn), заданная в некоторой области
D . Предположим, что эта функция имеет частные производные по
каждой переменной xi, (i=1,…,n): Эти производные называются
частными производными первого порядка. Они, вообще говоря,
также являются функциями от n действительных переменных.
Может случиться, что каждая из этих производных снова имеет
частные производные. Производные от первых производных
называются частными производными второго порядка. Если
существуют производные от вторых производных, то они
называются частными производными третьего порядка и т.д.
11.
Для функции z=f(x;y) по определению имеем:2 z z
(
)
z xx = x 2 = x x = [ f x ( x, y )] x
f xx ( x, y )
2 z z
z yy = y 2 = y ( y ) = [ f y ( x, y)] y
f yy ( x, y)
;
;
z z
z xy = x y = y ( x ) = [ f x ( x, y)] y
f xy ( x, y)
;
z z
z yx = y x = x ( y ) = [ f y ( x, y)] x
f yx ( x, y)
.
2
2
12.
13.
Производные z″xy и z″yx называются смешанными частнымипроизводными. В рассмотренном примере смешанные частные
производные оказались равными, т.е. z″xy=z″yx. При выполнении
некоторых условий данное равенство всегда справедливо.
Теорема.
Если функция z=f(x;y) обладает в некоторой точке непрерывными
частными производными z xy и z yx , то эти производные равны между
собой в данной точке
или
z xy = z yx
2z
2z
=
x y y x
Подобный результат имеет место и для других смешанных
производных.
Например, если непрерывны производные
они равны между собой:
3z
3z
3z .
=
=
y x y
x y 2
y 2 x
3 z
x y 2
;
3z ;
y x y
3z
y 2 x
, то
14.
Дифференцирование сложной функции.Функция нескольких аргументов называется сложной, если сами аргументы
являются функциями одной или нескольких переменных.
Пусть z=f(x; y) функция двух переменных и каждая из которых является
функцией независимой переменной t, где х=х(t); y=y(t).
Тогда сложная функция z от t может быть записана так:
z=f[x(t); y(t)], где x и y –промежуточные переменные .
Теорема.
Если z=f(x; y) дифференцируема в точке M(x;y) D и х=х(t); y=y(t) имеют
производные по t, то производная сложной функции z(t)=f[x(t);y(t)]
вычисляется по формуле
=
+
15.
Доказательство.Пусть t получает приращение , тогда x и y получают приращения
соответственно, а функция z получит приращение
. Поскольку функция
z=f(x;y) дифференцируема, то её полное приращение можно представить в
виде:
z=
x+
, где
y+
Разделим обе части этого равенства на
=
+α
+
+β
Перейдем к пределу при
в силу непрерывности
функций х=х(t) и y=y(t), которые по условию теоремы дифференцируемы, а
значит непрерывны. Следовательно α 0, β
Получаем:
тогда имеем:
=
+
+0
; или
=
+
16.
Пример., если z=x
Найти
2
где x=t +1, y=arctgt.
Решение.
=
=
=x
;
+
;
=
;
17.
Дифференцирование неявных функций.Функция z=f(x;y) называется неявной, если она задается уравнением
F(x;y;z)=0, неразрешенным относительно z. Найдем частные производные
и
. Для этого продифференцируем тождество F(x;y;f(x;y))≡0 по х и по у, если
F’z≠0
=
+
=
+
18.
Пример.Найти частные
z3=3xyz+a3
производные
функции
z(x,y),
Решение.
Здесь
F(x;y;z)= z3-3xyz-a3
F х=-3уz
F z=3z²-3xy
F y=-3xz
=
=
заданной
уравнением
19.
Литература.• Боронина Е.Б. Математический анализ [Электронный ресурс]:
учебное пособие/ Боронина Е.Б.— Электрон. Текстовые
данные.— Саратов: Научная книга, 2012.— 159 c.— Режим
доступа: http://www. iprbooksho p.ru/6298. — ЭБС «IPRbooks»
• Письменный, Д. Т. Конспект лекций по высшей математике.
Полный курс [Текст] : [учебное пособие] / Д. Т. Письменный. - 9-е
изд. - Москва : Айрис-пресс, 2010. - 603 с. : ил., табл. - (Высшее
образование). - ISBN 978-5-8112-4073-9
• Шипачев, В. С. Курс высшей математики [Текст] : учебник для
вузов / В. С. Шипачев ; под ред. А. Н. Тихонова ; - 4-е изд., испр. Москва : Оникс, 2009. - 600 с. : ил. - ISBN 978-5-488-02067-2















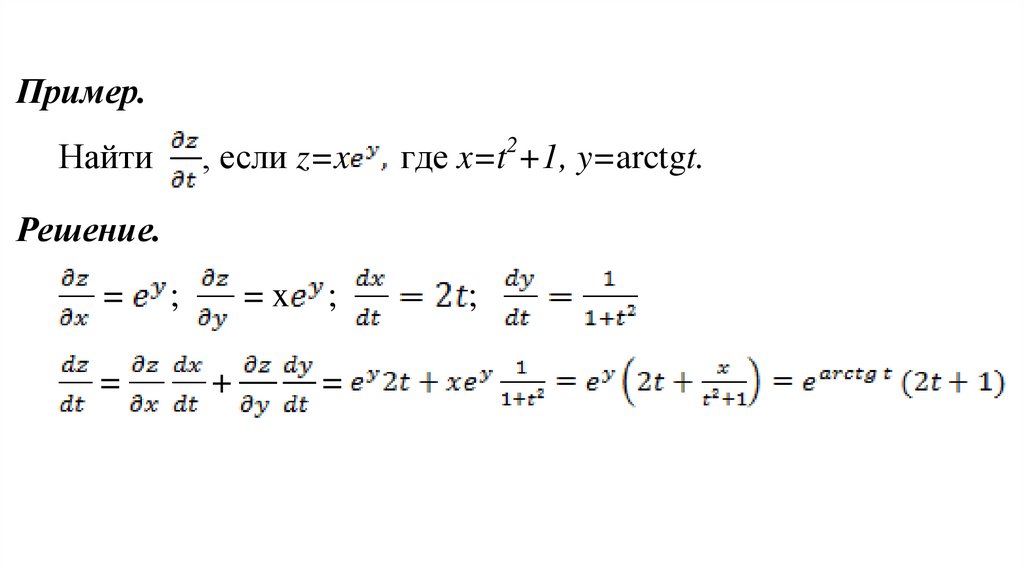



 Математика
Математика








