Похожие презентации:
Линейный интеграл в векторном поле, его свойства. Работа силового поля
1. Лекция 31. Линейный интеграл в векторном поле, его свойства. Работа силового поля. Циркуляция векторного поля, ее
гидродинамический смысл и вычисление.Формула Стокса. Ротор векторного поля, его
физический смысл. Плотность циркуляции.
Безвихревое поле, потенциальное поле.
Оператор Гамильтона, его свойства. Оператор
Лапласа.
1
2. § 1. Линейный интеграл в векторном поле. Циркуляция векторного поля.
Пусть в 3-х мерном пространстве задановекторное поле,
a Pi Qj Rk
где P,Q,R интегрируемы вместе со своими
производными. Пусть в пространстве
задана гладкая ориентированная кривая AB.
2
3.
В силу гладкости в каждой точке AB существуетединственный вектор касательной, который
может быть записан следующим образом:
3
4.
cos i cos j cos k, , - углы которые составляет вектор
с осями координат.
Считаем, что дуга AB задана
параметрически:
AB:
x x(t )
y y (t )
z z (t )
a t b
4
5.
Тогда для координат единичного векторакасательной имеем:
cos
cos
cos
xt
2
2
2
xt yt zt
yt
xt 2 yt 2 zt 2
zt
xt 2 yt 2 zt 2
где соответствуют ориентации вектора
совпадающего с ориентацией дуги AB, и не
совпадающей с ориентацией дуги
соответственно.
5
6.
Длина элемента дуги может быть найдена по2
2
формуле
2
dl xt yt zt dt
Рассмотрим в каждой точке дуги AB скалярное
произведение (a )
(a ) P cos Q cos R cos
Скалярное произведение представляет собой
непрерывную по координатам x,y,z функцию.
Из непрерывности скалярного произведения
следует что существует:
(a ) dl
AB
6
7.
Этот интеграл называется линейныминтегралом в векторном поле.
Смысл интеграла:
Пусть по дуге AB от действия вектора силы a
движется материальная точка единичной массы.
Скалярное произведение a ïð a
есть проекция вектора a на единичный вектор
касательной.
Если проекция пр a dl dA получим
элементарную
работу, совершенную силой
a на перемещении dl в направлении вектора .
7
8.
Чтобы найти полную работу, необходимопроинтегрировать по всей длине дуги AB:
A пр adl (a )dl - полная работа.
AB
AB
Смысл линейного интеграла - работа,
совершенная эти полем.
Определение. (циркуляции векторного
поля). Если существует в векторном поле a
линейный интеграл по ориентированному
замкнутому контуру вида:
(a )dl
8
9.
то значение этого интеграла называетсяциркуляцией векторного поля и
обозначается буквой Ц.
Ц (a )dl
l
Таким образом, циркуляция векторного
поля есть работа векторного поля при
движении по замкнутому контуру.
9
10. § 2. Теорема Стокса.
Если в 3-х мерном пространстве функцииP(x,y,z), Q(x,y,z), R(x,y,z), таковы, что:
1) Непрерывны вместе со своими
производными
P Q R
,
,
x y z
2) В пространстве задан гладкий,
ориентированный, замкнутый,
ограниченный контур
10
11.
3) Задана гладкая ориентированнаяповерхность S, натянутая на контур такая
что, нормаль к поверхности и обход контура
совмещены по правилу Буравчика. Тогда
Q P
Pdx Qdy Rdz dxdy
x y
S
R Q
P R
dydz
dzdx
z x
y z
11
12.
Формула, связывающаякриволинейный интеграл по
замкнутому контуру натянутая на
поверхность S называется формулой
Стокса.
В частном случае, если поле плоское,
R = 0, z = const, формула Стокса
переходит в формулу Грина.
12
13. § 3. Ротор векторного поля. Векторная запись теоремы Стокса.
Пусть имеется векторное поле вида:a Pi Qj Rk где P,Q,R непрерывны со
своими производными. Рассмотрим в
векторном поле замкнутый, гладкий,
ориентированный контур ℓ, который является
краем гладкой ориентируемой поверхности S.
Нормаль к поверхности S и обход контура
связаны по правилу Буравчика.
13
14.
Найдем работу, которуюсовершает векторное
поле aпри движении по
замкнутому контуру ℓ.
A (a )dl
( P cos Q cos R cos )dl Pdx Qdy Rdz
Так как на контур ℓ натянута ориентируемая
поверхность S, то
Rdz
Pdx Qdy
Q P
R Q
P R
dxdy
dydz
dzdx
z x
x y
y z
S
14
15.
Учитывая связь между поверхностнымиинтегралами 2-го и 1-го рода имеем:
S
Q P
R Q
P R
cos(nk ) cos(n i ) cos(nj ) ds
z x
y z
x y
Выражение, стоящее под знаком
поверхностного интеграла 1-го рода можно
записать как скалярное произведение:
15
16.
Q P R Q P R;
;
M
x y y z z x
y
z
x
и единичного вектора нормали к поверхности
n cos(n i ), cos(nj ), cos(nk )
Таким образом, работа по замкнутому
контуру может быть записана:
A (a )dl
S
(M n )ds
16
17.
Вектор M характеризует вращательнуюспособность поля. Если он равен 0, то поле не
совершает работу при движении по
замкнутому контуру.
Вектор M называется ротором векторного
поля (вихрем векторного
поля) и
обозначается: M rot a
i
rota
x
P
j
y
Q
k
R Q
i
z
y z
R
P R Q P
j k
z x
x y
17
18. Векторная запись теоремы Стокса
Теорема Стокса связывает:Pdx Qdy Rdz
S
Q P
R Q
dxdy dzdy
x y
y z
P R
dxdz
z x
Слева в формуле стоит циркуляция
векторного поля a по замкнутому контуру ℓ.
18
19.
(a )dl(rota n )dS
S
Это векторная запись теоремы Стокса.
Смысл:
Циркуляция векторного поля равна потоку
ротора этого векторного поля через
поверхность S, натянутую на контур ℓ.
19
20. § 4. Плотность циркуляции, связь её с ротором.
Пусть в векторном полеa Pi Qj Pk
В произвольной точке
пространства M задан вектор n.
Найдем циркуляцию векторного поля a по
замкнутому контуру ℓ, описываемому около
точки M и лежащему в плоскости,
перпендикулярной вектору a .
20
21.
Ц (a )dll
Если циркуляцию разделим на площадь
контура ℓ, то получим число,
характеризующее среднюю плотность
циркуляции в контуре ℓ.
( a ) dl
Ц
S
S
21
22.
Определение. (плотности циркуляции)Плотностью циркуляции
в точке М по
направлению вектора n называется число,
обозначаемое Г n (M ) и вычисляемое по формуле:
(a )dl
Г n ( М ) lim
S
l M
Когда контур ℓ стягивается в точку M.
Можно показать, что плотность циркуляции
в
точке M по направлению вектора n равна
проекции ротора
векторного поля на
направление n.
Г пр rota
n
n
22
23.
§ 5. Вычисление циркуляции.Ее можно вычислить 2 способами:
1) По определению, путем сведения к
криволинейному интегралу 2-го рода.
2) С помощью теоремы Стокса.
Пример: На практике.
24.
Виды векторных полей.§ 6. Потенциальное поле.
Определение. Векторное поле a называется
потенциальным, в некоторой односвязанной
области
V,
если
существует
такая
функция
,
что a grad .
Замечание. Функцию называют
потенциалом векторного поля a.
25.
Пример: На практике.q
2
2
2
r x y z
4 0
grad
i
j
k
x
y
z
2
( (x y2 z2 )
4 0 x
q
1
2
i ( ) j ( )k )
y
z
q 1
2x
2 y
2z
i
j
k
3
3
3
2( ) 2
2
4 0 2 ( x 2 y 2 z 2 ) 2
2
(
)
q
q
( xi yj zk )
r
3
3
4 0 r
4 0 ( x 2 y 2 z 2 ) 2
E
26.
Теорема. (необходимое и достаточноеусловие потенциальности).
Для
того,
чтобы
векторное поле a было потенциальным в
некоторой односвязанной области V,
необходимо и достаточно, чтобы циркуляция
этого векторного поля по любому замкнутому
контуру, лежащему в области V была равна
нулю.
Доказательство.
Самостоятельно.
27.
Замечание. Потенциал векторного поляопределен с точностью до константы.
a
Если
потенциал
векторного
поля
, то
есть a = grad , то + с – так же потенциал
векторного поля a .
0
grad( + с) = grad + gradс = a .
Для отыскания потенциала поля берут и
фиксируют определенную точку в поле, в
которой потенциал известен (бесконечно
удаленную точку, в которой = 0) и
M
применяют формулу:
( Ì ) ( M 0 )
d
M0
Pdx Qdy Rdz
MM 0
28.
Точка M0 - фиксированная точка, в которойпотенциал известен.
Точка M - точка, в которой потенциал
неизвестен.
P,Q,R - координаты векторного поля, для
которого
находим потенциалы.
MM 0 - произвольная дуга, соединяющая две
точки M0 и M.
Дуга берется произвольной в силу того, что
интеграл 2-го рода не зависит от способа
движения от точки M0 к точке M, а зависит
только от расположения этих точек в случае
потенциального поля.
29.
§ 7. Безвихревые поля.Определение: Векторное поле a называется
безвихревым в односвязанной области V,
если ротор этого векторного поля равен 0.
rot a = 0.
Теорема. (необходимое и достаточное
условие безвихревого поля):
Для того, чтобы векторное поле было
безвихревым необходимо и достаточно,
чтобы оно было потенциальным в каждой
точке некоторой области V.
30.
ДоказательствоНеобходимость:
Пусть векторное поле a - безвихревое, то
есть rota 0 .
Циркуляция векторного поля a , по
произвольному замкнутому контуру l
вычисляется по формуле, которая с учетом
теоремы Стокса дает интеграл по поверхности S
Ö
a
dl
rot
a
n
dS
l
S
Ö 0 (по произвольному замкнутому контуру).
В силу предыдущей теоремы это означает что
a - потенциальное поле.
30
31.
Достаточность:a - потенциальное поле a grad rot a
rot grad 0 поле a – безвихревое.
§ 8. Соленоидальные поля.
Определение: Векторное поле a называется
соленоидальным в односвязанной области V,
если: diva 0
Теорема. (о соленоидальности векторного
поля). Для того, чтобы векторное поле a было
соленоидальным в односвязанной области V
необходимо и достаточно, чтобы поток
векторного поля через произвольную
замкнутую поверхность, лежащую в области V,
был равен нулю.
31
32.
Необходимость:Пусть a - соленоидальное поле diva 0 .
Рассмотрим в области V произвольную
замкнутую поверхность V, ориентированную
внешней нормалью
V
s
(a n )dS
теор.Острогр.
S
diva dV 0
V
n
Достаточность:
Предположим что поток через поверхность = 0.
diva lim
S M
(a n )dS
S
VS
0
32
33.
Свойства соленоидальных полейПусть дано векторное поле a . Считаем, что в
поле построены векторные линии.
Возьмем в поле замкнутый
контур и через него проведем
множество векторных линий.
Это множество линий
образует векторную трубку.
33
34.
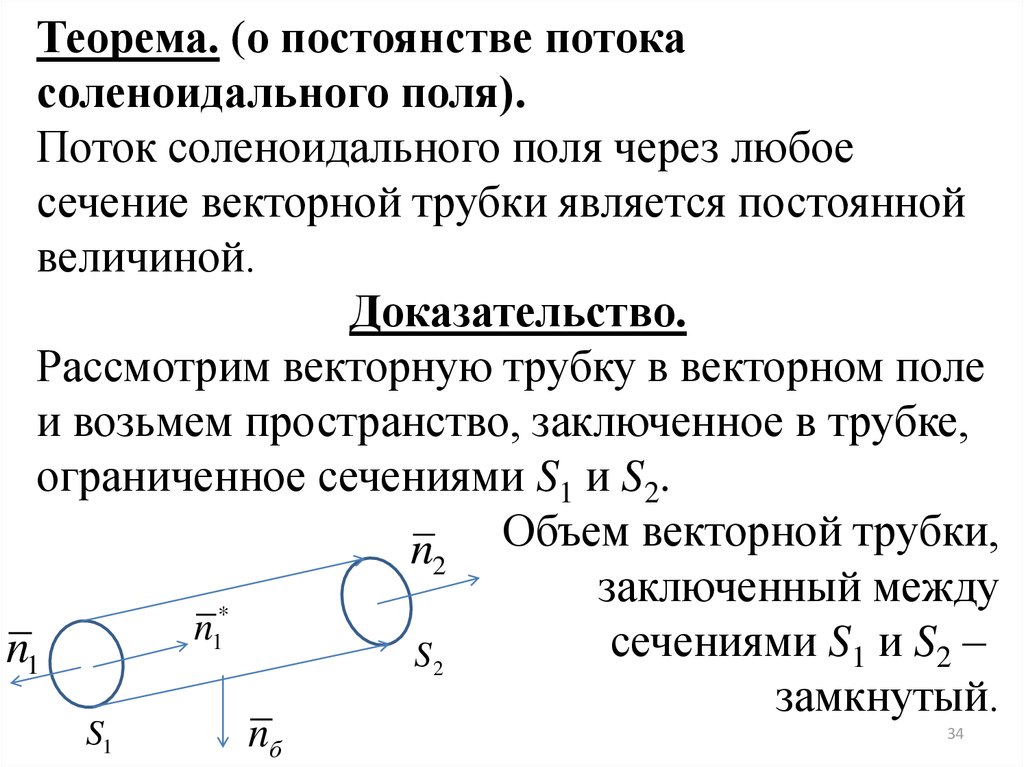
Теорема. (о постоянстве потокасоленоидального поля).
Поток соленоидального поля через любое
сечение векторной трубки является постоянной
величиной.
Доказательство.
Рассмотрим векторную трубку в векторном поле
и возьмем пространство, заключенное в трубке,
ограниченное сечениями S1 и S2.
n2 Объем векторной трубки,
заключенный
между
n1*
сечениями S1 и S2 –
n1
S2
замкнутый.
S1
nб
34
35. Поверхность, ограничивающая объем состоит из 3-х поверхностей , и , которые имеют единичные нормали , , , направленные как
Поверхность, ограничивающая объем состоитиз 3-х поверхностей S1 , S 2 и S á , которые
имеют единичные нормали n1 , n2 , nб ,
направленные как указано на рисунке.
Поток векторного поля a через поверхность S:
S = S1 + S2 + Sб
можно вычислить по теореме Остроградского:
a n dS diva dV
S
V
Векторное поле соленоидально
Откуда следует, что
diva 0
a
n
dS
a
n
dS
a
n
dS
0
a
n
dS
0
1
S
S1
б
2
S2
Sб
35
36.
В силу определения векторной трубкиa nб a nб 0, а следовательно,
интеграл = 0.
a n1 dS a n2 dS 0
s1
s2
При вычислении потока через поверхность
смотрят за направлением нормали к этой
поверхности. При вычислении потока через S1
считаем, что нормаль направлена в сторону
потока. При вычислении потока S 2 берем
нормаль, направленную в сторону потока.
*
n1
n1
a
n
dS
a
1
s1
s1
*
n1
dS
36
37.
Заменим поток в направлении n1 на поток внаправлении n1* имеем:
a n dS a n
*
1
S1
Ï
S1
Ï
2
dS 0
S2
S2
0 Ï
S2
Ï
S1
Поток в трубке постоянен по сечению в
случае соленоидального поля.
37
38.
§ 9. Операции 1 и 2 порядка над скалярнымии векторными полями.
Пусть есть скалярное поле x, y, z и векторное
поле a x, y, z .
Каждому скалярному полю с помощью градиента
можно поставить векторное поле градиента.
Любому дифференциальному векторному полю с
помощью div можно поставить скалярное поле.
Любому векторному полю с помощью rota
можно поставить векторное поле.
grad , diva , rota - операции 1-го порядка. Они
показывают, что операции связаны между собой.
38
39.
Операции 1-го порядка порождают 5 операций2-го порядка.
1. div grad
Дивергенция берется
2. div rota
от векторного поля.
3. grad diva
4. rot grad
5. rot rota
Две из операций 2-го порядка равны 0.
39
40.
diva i diva j diva kgrad diva
x
y
z
2P
2 Q 2 2 P 2Q 2 R 2 P 2 Q 2 R
j
2
R i
2
2 k
x y x z x y y
y z x z z y z
x
Раскрытие всех операций производится слева
направо. Все они приводятся к вычислению
частных производных 2-го порядка.
i
rot grad
x
x
j
y
y
k
0
z
z
Это первая
из операций
2-го порядка,
которая = 0.
40
41.
Рассмотрим:rot x a rot y a rot z a
div rota
x
y
z
R Q P R Q P
x y z y z x z x y
R Q P R Q P
0
x y x z y z y x z x z y
Это вторая операция 2-го порядка, которая
равно нулю.
2
0
2
0
2
0
2
0
2
0
2
0
rot grad 0
div rota 0
41
42.
Операцию 2-го порядка div gradназывают
оператор Лапласа и обозначают:
∆ - оператор Лапласа (Лапласиан)
div grad
x x y y z z
2 2 2
2 2 2
x
y
z
Сравнивая
записать:
обведённые
выражения
можем
2
2
2
2 2
2
x y z
42
43.
Для электростатического поля, в случаестационарного поля.
div E = - объемная плотность заряда
E = grad
Электростатическое поле E является
потенциальным
div grad - уравнение Лапласа.
В случае электростатического поля функция
потенциала подчиняется уравнению , где
- неизвестная заранее функция.
43
44.
§ 10. Символика Гамильтона.Для того, чтобы удобно работать с операциями
1-го и 2-го порядка, Гамильтон ввел следующее
понятия:
grad
i
j
k
x
y
z
Обозначить символом и назвать его
оператором «Набла».
i
j k
x
y
z
44
45.
Операции 1-го порядка записываются в виде:grad
a x a y a z
div a
a - скалярное
x
y
z
произведение
i
j
k
векторное
rot a
a
x y z
произведение
ax a y az
Запись операций 2-го порядка с помощью
оператора Набла:
2
div
grad
grad
1)
2 - оператор Лапласа равен оператору
Набла в квадрате.
45
46.
Тогда: div grad2) div rot a rota a 0
3) grad diva a
4) rot grad grad 0
5) rot rota a
46













































 Физика
Физика








