Методы минимизации функций при отсутствии ограничений: обзор

1.

Методы минимизации функций при отсутствии
ограничений: обзор
Пример: задача идентификации – требуется найти вектор из условия минимума критерия
J N ( ) 1 /( 2 N ) k 0 || y(k 1) g (k , (k ), ) || 2 .
N
1 Условия минимума гладких функций
Пусть задана функция f ( x) : R n R .
Определение 1. Точка x * называется локальным минимумом f (x) на R n , если найдется 0 такое, что f ( x) f ( x * ) для всех x
из -окрестности x * , т.е., || x x * || , где || x || 2 ( x12 ... x n2 ) ̶ евклидова норма.
Определение 2. Точка x * называется глобальным минимумом f (x) на R n , если f ( x) f ( x * ) для всех x R n .
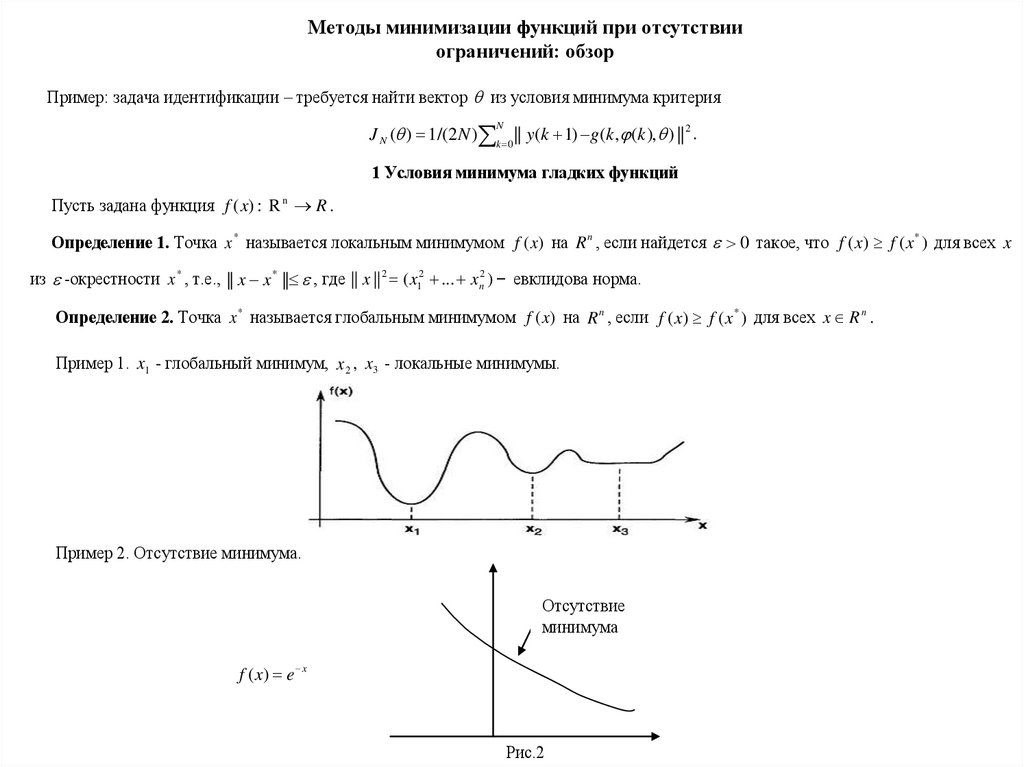
Пример 1. x1 - глобальный минимум, x 2 , x3 - локальные минимумы.
Пример 2. Отсутствие минимума.
Отсутствие
минимума
f ( x) e x
Рис.2

2.

Теорема 1. (Ферма). Пусть x * точка минимума f (x) на R n и f (x) дифференцируема в точке x * . Тогда
f ( x * ) 0 ,
где f ( x) ( f ( x) / x1 ,..., f ( x) / x n ) T - градиент f (x) .
(1)
Теорема 2. Пусть в точке x * f (x) дважды дифференцируема и выполняется необходимое условие
f ( x * ) 0
и при этом
2 f ( x* ) 0 ,
(2)
где
2 f ( x) / x12
.
.
2 f ( x)
.
.
2 f ( x) / x x
1
n
*
Тогда x - точка локального минимума.
.
.
.
.
.
.
.
.
2 f ( x) / x1 x n
.
.
- Гессиан.
.
.
2
2
f ( x) / x n
Отметим, что Гессиан – симметричная матрица, а условие A 2 f ( x * ) 0 означает положительную определенность этой
матрицы. Т.е., для y R n , y 0 выполняется условие
y T Ay 0 .
Опираясь на эти утверждения, задача поиска минимума может быть сведена к поиску решений системы нелинейных уравнений
f ( x ) 0
и проверке выполнения условия (2) на полученном решении.

3.

2 Градиентный метод
Пусть f ( x) C 1 ( R n ) . В этом случае наиболее простым методом минимизации f (x) является градиентный
xk 1 xk k f ( xk ) , k 0,1,...,
(3)
где x 0 - задано, k - определяет длину шага.
Основан на следующей идее. Мы начинаем в некоторой точке x 0 и генерируем векторы x1 , x2 ,... такие, что f (x) уменьшается в
каждой итерации, т.е.
f ( xk 1 ) f ( xk ) .
(4)
Имеем
f ( x k 1 ) f ( x k ) f T ( x k )( x k 1 x k ) o(|| x k 1 x k ||)
f ( xk ) k || f ( xk ) ||2 o(|| xk 1 xk ||) ,
где ( z ) o(|| z ||) - функция, удовлетворяющая условию
lim z 0 ( z ) / z 0 .
При k достаточно малом второе слагаемое доминирует над третьим и f ( xk 1 ) f ( xk ) .
Первая проблема, возникающая при реализации метода это выбор k . Достаточно малый шаг обеспечит убывание функции, но
может привести к неприемлемо большому количеству итераций, необходимого для достижения точки минимума. С другой стороны,
слишком большой шаг может приводить к невыполнению условия (4), либо к колебательности около точки минимума.
Пример. f ( x) ax 2 , a 0 .
Рис.2

4.

Алгоритм принимает вид
xk 1 (1 2 k a) xk .
Пусть k const и 0 1/ a . Тогда последовательность будет сходиться к x * 0 , а при 1/ a расходиться.
Один из возможных вариантов выбора k состоит в обеспечении максимального уменьшения f (x) на каждой итерации
k arg min 0 f(x k f ( xk )) .
(5)
В этом случае градиентный метод (ГМ) называются методом наискорейшего спуска (МНС).
Если для некоторого k
f ( xk ) 0 ,
то точка x k удовлетворяет условию (1). Мы можем использовать в качестве основы для правила остановки алгоритма:
|| f ( xk ) || ,
(6)
где 0 - заданное пороговое значение.
Возможные альтернативы:
| f ( xk 1 ) f ( xk ) | ,
(7)
|| xk 1 xk || .
(8)
Или, используя относительные величины (аналоги (6)-(8))
| f ( xk 1 ) f ( xk ) | / | f ( xk ) | ,
|| xk 1 xk || / || xk || .
(9)
(10)
Относительные критерии более предпочтительны, так как не зависят от шкалы измерения переменных. Для того, чтобы избежать
деления на очень малые числа, критерии останова можно модифицировать:
| f ( xk 1 ) f ( xk ) | / max( 1, | f ( xk ) |) .
(11)

5.

ГМ является примером итерационного алгоритма. Это означает, что алгоритм генерирует последовательность точек, каждую на базе
предыдущей.
Определение 3. Говорят, что итерационный алгоритм глобально сходится, если для любой начальной точки алгоритм генерирует
последовательность точек, сходящуюся к точке, удовлетворяющей необходимому условию (1).
Это можно сформулировать еще так: для x0 R n , 0 , N 0 такие, что при k N будет выполняться условие || x k x * || .
В случае, когда алгоритм глобально не сходится , он может все еще генерировать сходящую последовательность при условии, что
начальная точка достаточно близка к точке минимума. Насколько близко к решению должна быть начальная точка зависит от
алгоритма.
Формальное определение локальной сходимости: для, 0 , 0 N 0 такие, что при || x 0 x * || будет выполняться
условие || x k x * || для всех k N .
Со сходимостью алгоритма тесно связана скорость его сходимости, т.е. насколько быстро алгоритм сходится к решению. Свойства
ГМ обсудим на примере квадратичной функции
f ( x) 1 / 2 x T Qx b T x ,
где b R n - постоянный вектор, Q - положительно определенная, симметричная матрица ( Q 0 ).
Единственная точка минимума определяется выражением
f ( x) Qx b 0 .
Откуда
x * Q 1b .
То, что это действительно точка минимума следует из выражения
2 f ( x* ) Q 0 .
Мы воспользовались следующими соотношениями при вычислении градиента:
T
b x bT
x b T ei ,
xi
xi
(12)

6.

T
x Qx (
x) T Qx x T Q
x eiT Qx x T Qe i 2eiT Qx ,
xi
xi
xi
где e i - i -единичный вектор.
Теорема 3. В МНС x k x * для любого x 0 .
Теорема 4. Для ГМ с фиксированным шагом x k x * для любого x 0 , если и только если
0 2 / max (Q) ,
где max (Q) - максимальное собственное число матрицы Q .
Собственные числа матрицы являются корнями ее характеристического уравнения
det( I Q) n ... q n 0 .
Пусть последовательность x k сходится к x * , т.е.
lim k || x k x * || 0 .
Определение 4. Говорят, что порядок сходимости метода есть p R , если
|| x k 1 x * || O(|| x k x * || p )
где ( z ) O(|| z ||) - функция, удовлетворяющая условию | ( z ) | / || z || const при z 0 .
Или по другому || x k 1 x * || C || x k x * || p , при || x k x * || 0
При p 1 - линейная сходимость, p 2 - квадратичная сходимость.
Теорема 5. Порядок сходимости МНС для квадратичной функции равен 1.

7.

3 Метод Ньютона
ГМ использует только производные первого порядка при генерировании последовательности, сходящейся к решению.
Использование производных более высокого порядка может приводить к более эффективным алгоритмам.
С помощью формулы Тейлора можно получить квадратичную аппроксимацию f (x) :
f ( x) f ( x k ) f T ( x k )( x x k ) 1 / 2( x x k ) T f 2 ( x k )( x x k ) .
Использование необходимого условия (1) дает
f ( x k ) f 2 ( x k )( x x k ) 0 .
Откуда следует метод Ньютона (МН)
x k 1 x k ( f 2 ( x k )) 1 f ( x k ) ,
(13)
в предположении, что f 2 ( x k ) невырожденная матрица.
Условие (4) f ( xk 1 ) f ( xk ) может не выполняться для МН, например, если x 0 далеко от решения. Несмотря на это МН быстрее
сходится, если x 0 достаточно близко к решению.
Для квадратичной функции нетрудно показать, что метод сходится за один шаг. Действительно, пусть
f ( x) 1 / 2 x T Qx b T x ,
где b R n - постоянный вектор, Q - положительно определенная, симметричная матрица ( Q 0 ). Тогда
f ( x) Qx b , 2 f ( x) Q .
Откуда следует
x1 x0 Q 1 (Qx 0 b) Q 1b x * .
Общий случай.
Теорема 6. Пусть f ( x) C 2 ( R n ) , f ( x * ) 0 и 2 f ( x * ) 0 . Тогда для любого x 0 достаточно близкого к x * МН сходится к x * с
порядком сходимости равным 2.

8.

4 Метод Левенберга-Маркардта
Если матрица f 2 ( x k ) не является положительно определенной, то последовательность, генерируемая МН может не удовлетворять
условию f ( xk 1 ) f ( xk ) . Предложена модификация МН
x k 1 x k ( f 2 ( x k ) k I ) 1 f ( x k ) ,
(14)
где k 0 .
Если k 0 , то имеем МН, а если k , то - ГМ. При использовании метода начинают с большого k , а затем медленно
уменьшают его значение до тех пор пока выполнится условие f ( xk 1 ) f ( xk ) .
5 Метод Гаусса-Ньютона
Рассмотрим задачу минимизации функции
f ( x) 1 / 2 i 1 ri2 ( x) ,
m
где ri ( x) : R n R , i 1,..., m - заданные функции.
Пример. Пусть требуется найти минимум функции вида
J N ( ) 1 /( 2 N ) k 0 ( y(k 1) g (k , (k ), )) 2 .
N
Тогда ri ( x) y(i 1) g (i, (i), x) , i 1,2,..., N .
Удобно перейти к векторно-матричным обозначениям
f ( x) 1 / 2r T ( x)r ( x) ,
где r ( x) (r1 ( x),..., rm ( x)) T .
(15)

9.

Для того, что бы воспользоваться МН необходимо найти градиент и Гессиан. Имеем
( f ( x)) j f ( x) / x j i 1 ri ( x) ri ( x) / x j .
m
Введем матрицу первых производных от r (x) (Якобиан)
r1 ( x) / x1
.
J ( x)
.
r ( x) / x
1
m
.
.
.
.
r1 ( x) / x n
.
. .
.
rm ( x) / x n
Градиент может быть представлен в виде
f ( x) J T ( x)r ( x) .
( k , j ) элемент Гессиана определяется выражением
2 f ( x) / xk x j / xk ( f ( x) / x j )
/ xk ( i 1 ri ( x) ri ( x) / x j ) i 1 ( ri ( x) / xk ri ( x) / x j ri ( x) 2 r j ( x) / xk x j ) .
m
m
Пусть S (x ) матрица ( k , j ) компоненты, которой определяются выражением
m
r ( x) 2 r j ( x) / xk x j .
i 1 i
Тогда Гессиан может быть представлен в виде
2 f ( x) J T ( x) J ( x) S ( x) .
Откуда следует представление для МН
x k 1 x k ( J T ( x) J ( x) S ( x)) 1 J T ( x)r ( x) .

10.

В некоторых случаях матрицей S (x ) можно пренебречь в этом выражении и МН сводится к методу Ньютона-Гаусса (МНГ)
x k 1 x k ( J T ( x) J ( x)) 1 J T ( x)r ( x) .
(16)
Матрица J T ( x) J ( x) может вырождаться. В этом случае можно использовать модификацию метода
x k 1 x k ( J T ( x) J ( x) k I ) 1 J T ( x)r ( x) .
Можно интерпретировать k I , как аппроксимацию S (x ) .
(17)

11.

5 Обсуждение
Задача. Пусть дана функция f ( x) : R n R .
Требуется найти min f ( x) , x R n .
Алгоритмы
1. ГМ
xk 1 xk k f ( xk ) , k 0,1,...,
(3)
где x 0 - задано, k - определяет длину шага.
2 НМ.
x k 1 x k ( f 2 ( x k )) 1 f ( x k ) ,
(13)
3. НГМ. Ищется минимум функции специального вида
f ( x) 1 / 2 i 1 ri2 ( x) ,
m
(15)
где ri ( x) : R n R , i 1,..., m - заданные функции.
x k 1 x k ( J T ( x) J ( x)) 1 J T ( x)r ( x) .
(16)
4. МЛМ
x k 1 x k ( J T ( x) J ( x) k I ) 1 J T ( x)r ( x) .
(17)

12.

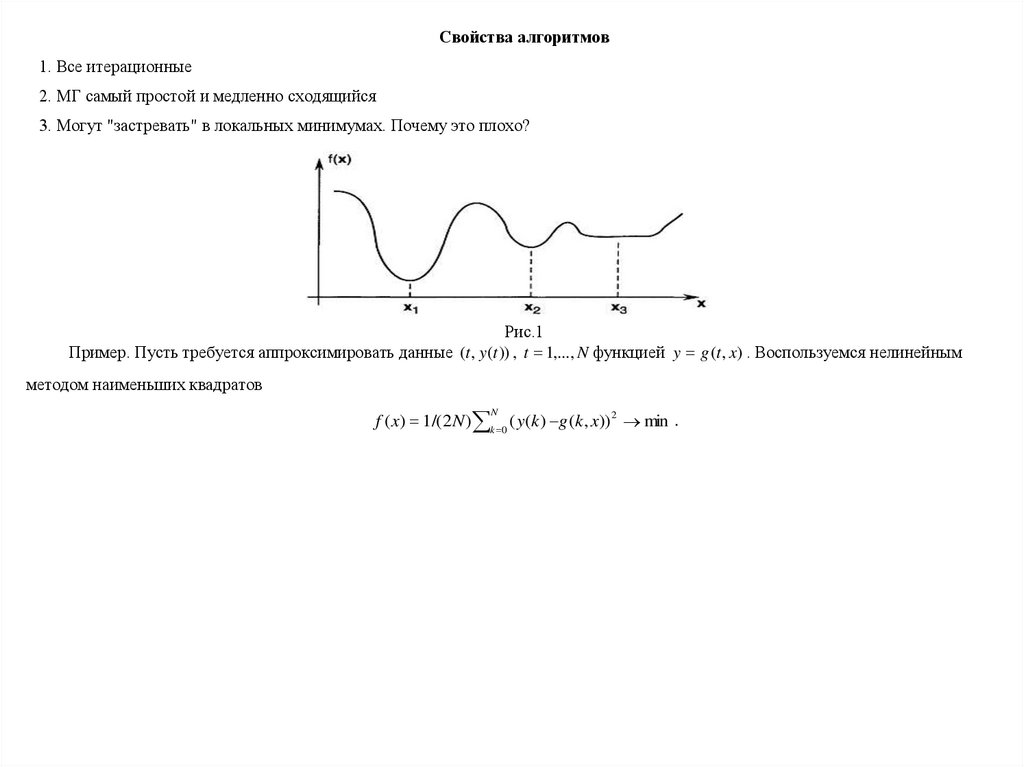
Свойства алгоритмов
1. Все итерационные
2. МГ самый простой и медленно сходящийся
3. Могут "застревать" в локальных минимумах. Почему это плохо?
Рис.1
Пример. Пусть требуется аппроксимировать данные (t , y (t )) , t 1,..., N функцией y g (t , x) . Воспользуемся нелинейным
методом наименьших квадратов
f ( x) 1 /( 2 N ) k 0 ( y(k ) g (k , x)) 2 min .
N

13.

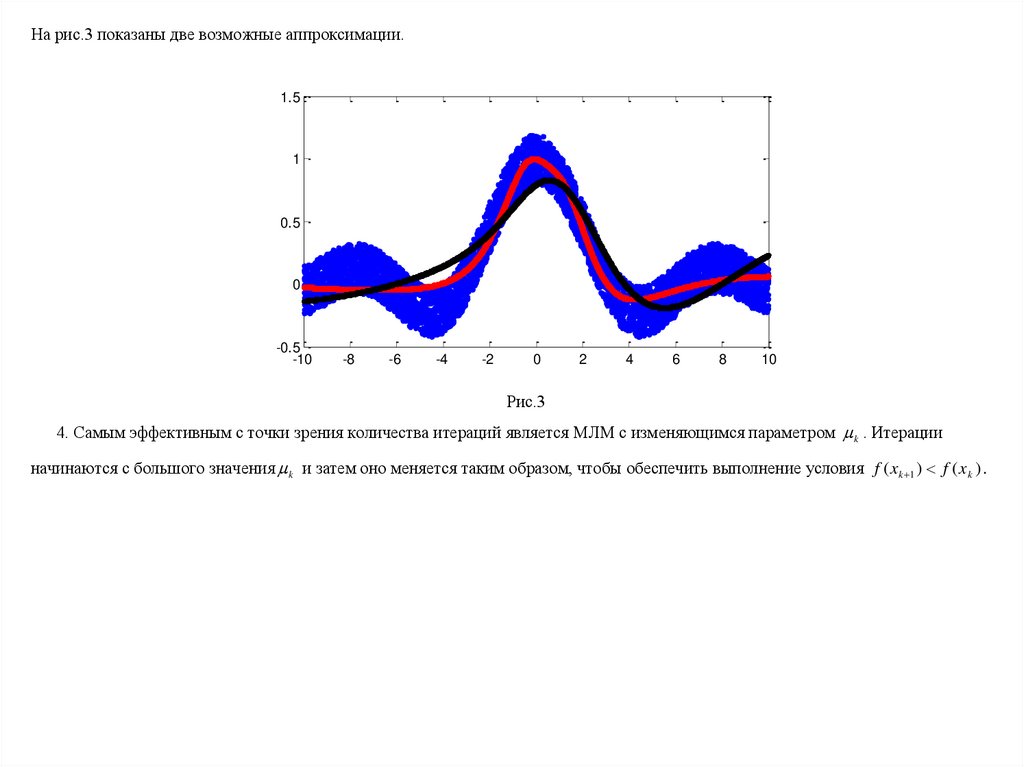
На рис.3 показаны две возможные аппроксимации.
1.5
1
0.5
0
-0.5
-10
-8
-6
-4
-2
0
2
4
6
8
10
Рис.3
4. Самым эффективным с точки зрения количества итераций является МЛМ с изменяющимся параметром k . Итерации
начинаются с большого значения k и затем оно меняется таким образом, чтобы обеспечить выполнение условия f ( xk 1 ) f ( xk ) .